Le Principe Franck-Condon décrit les intensités des transitions vibroniques, ou l’absorption ou l’émission d’un photon. Il indique que lorsqu’une molécule subit une transition électronique, telle que l’ionisation, la configuration nucléaire de la molécule ne subit aucun changement significatif. Cela est dû en fait au fait que les noyaux sont beaucoup plus massifs que les électrons et que la transition électronique s’effectue plus rapidement que les noyaux ne peuvent répondre. Lorsque le noyau se réaligne avec la nouvelle configuration électronique, la théorie stipule qu’il doit subir une vibration.
Si nous imaginons la transition verticale du sol à l’état électronique excité comme se produisant à partir d’une fonction d’onde vibratoire qui donne une distribution de probabilité de trouver les noyaux dans une région donnée de l’espace, nous pouvons déterminer la probabilité d’un niveau vibratoire donné à partir de l’intégrale de chevauchement \(S_{v’, v}\) qui donne le chevauchement de la fonction d’onde vibratoire dans le sol et l’état excité. Les nombres quantiques \(v’\) se réfèrent à l’état fondamental et les nombres quantiques \(v\) se réfèrent à l’état excité. La probabilité de transition peut être séparée en parties électroniques et nucléaires en utilisant l’approximation de Condon.
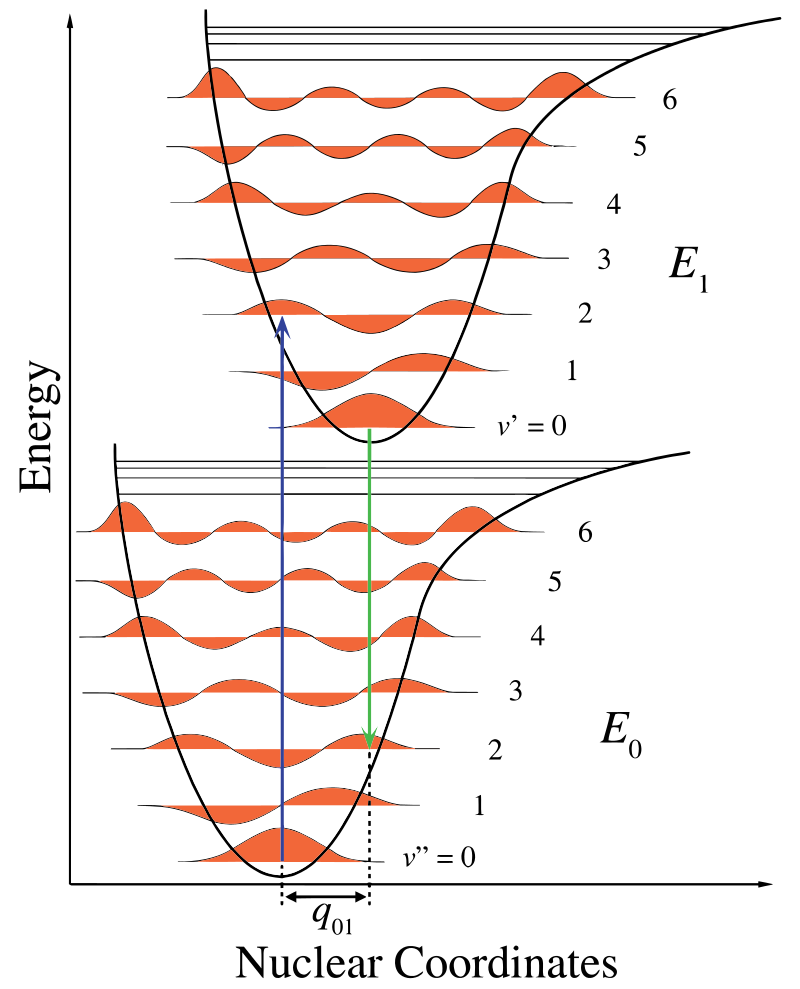
Dans la figure \(\PageIndex{1}\), l’axe nucléaire montre une conséquence de la séparation internucléaire et la transition vibronique est indiquée par les flèches verticales bleues et vertes. Cette figure démontre trois choses:
- Une absorption conduit à un état d’énergie plus élevé,
- la fluorescence conduit à un état d’énergie plus faible, et
- le déplacement des coordonnées nucléaires entre le sol et l’état excité indique une nouvelle position d’équilibre pour le potentiel d’interaction nucléaire. Le fait que la flèche de fluorescence soit plus courte que l’absorption indique qu’elle a moins d’énergie, ou que sa longueur d’onde est plus longue.
L’approximation classique de Condon
L’approximation de Condon est l’hypothèse que la transition électronique se produit sur une échelle de temps courte par rapport au mouvement nucléaire, de sorte que la probabilité de transition peut être calculée à une position nucléaire fixe.
Ce changement de vibration est maintenu pendant un état appelé excitation électronique rapide. Les forces coulombiques résultantes produisent un équilibre comme le montre la figure pour les noyaux appelés point tournant. Le point de retournement peut être cartographié en traçant une ligne verticale depuis le minimum de la courbe inférieure jusqu’à l’intersection de l’état électronique supérieur. Cette procédure est appelée transition verticale et a déjà été discutée dans le contexte de la spectroscopie photoélectronique (une autre spectroscopie électronique)..
Le principe de Franck-Condon explique les intensités relatives des transitions vibroniques en reliant la probabilité d’une transition vibrationnelle au chevauchement des fonctions d’ondes vibratoires. Il indique que la probabilité qu’une transition vibrationnelle se produise est pondérée par l’intégrale de chevauchement de Franck-Condon :
\
Dans l’approximation de Franck-Condon, les noyaux sont considérés comme « fixes » lors des transitions électroniques. Ainsi, les transitions électroniques peuvent être considérées comme des transitions verticales sur des courbes électroniques d’énergie potentielle (transitions viériques dans la figure \(\PageIndex{1}\)).
Le Principe quantique Franck-Condon
Le Principe Franck-Condon a à la fois une application classique et quantique. Classiquement, le principe de Franck–Condon est l’approximation selon laquelle une transition électronique est la plus susceptible de se produire sans modification des positions des noyaux dans l’entité moléculaire et son environnement. L’état résultant est appelé état Franck-Condon, et la transition impliquée, une transition verticale. La formulation mécanique quantique de ce principe est que l’intensité d’une transition vibronique est proportionnelle au carré de l’intégrale de recouvrement entre les fonctions d’onde vibrationnelles des deux états impliqués dans la transition.
Le principe de Franck-Condon est basé sur l’approximation de Born-Oppenheimer, qui permet de séparer les fonctions d’onde électronique \(q\) et nucléaire \(Q\) compte tenu de la fonction d’onde totale.
\
Puisque l’opérateur de transition, \(\hat{\mu}(q)\), ne dépend que du composant électronique, les composants nucléaires peuvent être séparés de l’intégrale de moment de transition qui dicte la probabilité que la transition se produise:
&=\underbrace{\langle\psi^{*}_{nuc, f}|\psi_{nuc, i}\rangle}_{\text{nuclear overlap}}\langle\psi^{*}_{el,f} |{\boldsymbol{\mu}}|\ psi_{el,i}\rangle\end{align}\]
Si l’intégrale de chevauchement nucléaire est nulle pour cette transition, alors la transition ne sera pas observée, quelle que soit la grandeur du facteur électronique.
\(S_{00}\) Transition Évaluée dans le Modèle d’oscillateur Harmonique
Le chevauchement nucléaire pour la transition zéro-zéro \(S_{00}\) peut être calculé tout simplement en utilisant la définition de la forme gaussienne des fonctions d’onde de l’oscillateur harmonique.
La fonction d’onde de point zéro dans l’état électronique de masse est
\
La fonction d’onde de point zéro dans l’état électronique excité est
\
où
- \(\alpha=\dfrac {\sqrt{mk }} {\hbar}\)
- \(R_e\) est la longueur de liaison d’équilibre dans l’état électronique de masse
- \(Q_e\) est la longueur de liaison d’équilibre dans l’état électronique excité
L’intégrale de chevauchement nucléaire est
\
L’exposant dans l’équation \(\ref{FC1}\) peut être développé comme
\
et nous utilisons
\
et
\
pour remplacer et compléter le carré à l’intérieur de l’intégrale. Nous pouvons exprimer
\.\]
Ainsi, l’intégrale dans l’équation \(\ref{FC2}\) est
\
L’intégrale est une intégrale gaussienne. Vous pouvez montrer que si nous laissons \(z= \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) alors \(dz= \sqrt{\alpha} dR\) et que l’intégrale devient
\
cette intégrale a déjà été résolue, à partir d’une table d’intégrales, l’équation \(\ref{FC3}\) devient
\
Nous suivrions la même procédure pour calculer ce chevauchement de la vibration de niveau zéro dans le sol au premier niveau vibratoire excité de l’état excité: \(S_{01}\).
\(S_{01}\) Transition évaluée dans le modèle d’oscillateur Harmonique
Pour calculer le chevauchement du niveau d’état fondamental zéro (\(v = 0\)) avec le premier niveau d’état excité (\(v’ = 1\)), nous utilisons le polynôme d’Hermite \(H_1(x) = 2x\) pour décrire la fonction d’onde de l’état excité (voir ici pour une revue des fonctions d’onde de l’oscillateur harmonique). Ici \(x = \sqrt{\alpha}(R-Q_e)\).
\
avec la fonction d’onde au point zéro dans l’état électronique de masse est
\
La première fonction d’onde à l’état excité dans l’état électronique excité est
\
Le chevauchement de zéro niveau d’état fondamental avec le premier niveau d’état excité (Équation \(\ref{FC01}\)) est alors
\
et
\
Les mêmes substitutions peuvent être faites comme ci-dessus pour que l’intégrale puisse être écrite comme (non montrée et à démontrer dans un devoir exercices) et le résultat final est
\
Nous pourrions continuer et calculer ce chevauchement du niveau zéro dans l’état fondamental avec tous les niveaux vibratoires de lumière plus élevés: \(S_{02}\), \(S_{03}\), etc. Chaque terme correspond à une transition avec une énergie différente puisque les niveaux vibratoires ont des énergies différentes. La bande d’absorption a alors l’apparence d’une progression (une progression Franck-Condon) de transitions entre différents niveaux ayant chacun sa propre probabilité.
Progressions de Franck-Condon
Pour comprendre la signification de la formule ci-dessus pour le facteur FC, examinons une surface d’énergie potentielle au sol et à l’état excité à \(T = 0\)Kelvin. On voit ci-dessous deux états séparés par 8 000 cm-1 d’énergie. Il s’agit de la séparation d’énergie entre les fonds de leurs puits potentiels, mais aussi entre les niveaux d’énergie du point zéro respectifs. Supposons que le nombre d’ondes du mode vibratoire est de 1000 cm-1 et que la longueur de liaison est augmentée du fait qu’un électron est retiré d’une orbitale de liaison et placé dans une orbitale anti-liaison lors de l’excitation électronique.
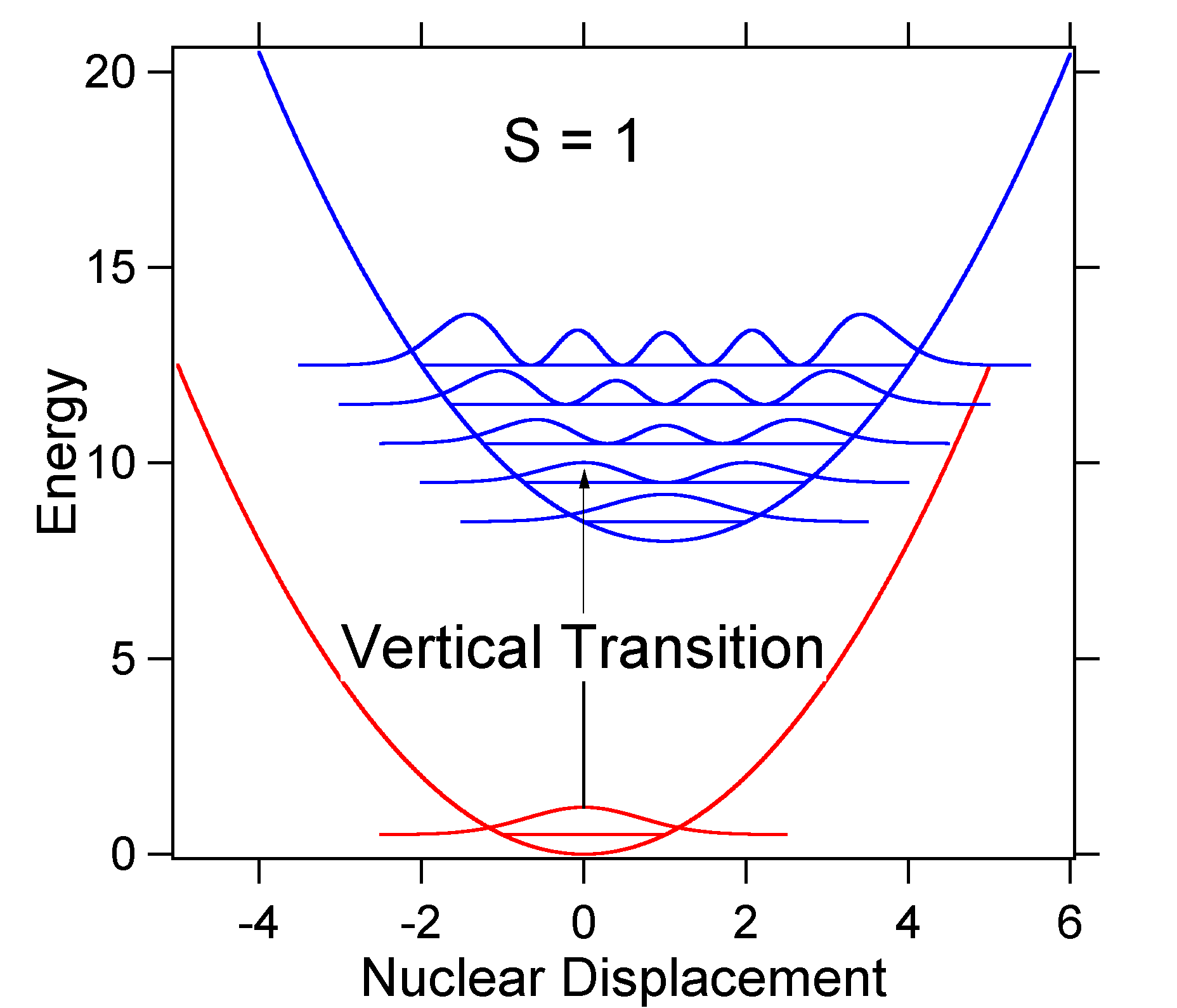
Selon le modèle ci-dessus pour le facteur Franck-Condon, nous générerions un spectre « stick » (Figure \(\PageIndex{3}\)) où chaque transition vibrationnelle est infiniment étroite et la transition ne peut se produire que lorsque \(E =h\nu\) exactement. Par exemple, les surfaces d’énergie potentielle ont été données pour S = 1 et la probabilité de transition à chaque niveau est donnée par les bâtons (noirs) dans la figure ci-dessous.
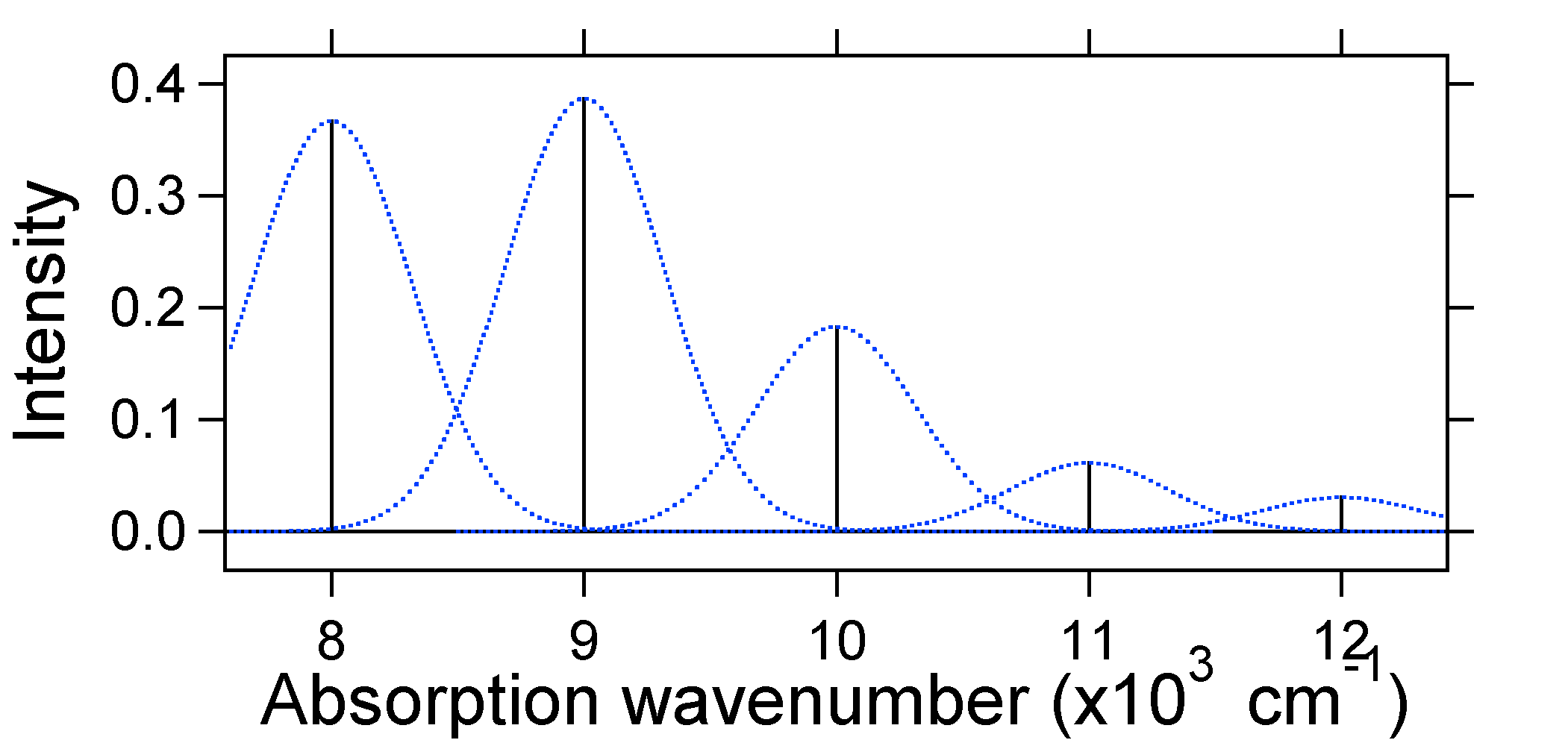
Les Gaussiens en pointillés qui entourent chaque bâtonnet donnent une image plus réaliste de ce à quoi devrait ressembler le spectre d’absorption. En premier lieu, chaque niveau d’énergie (bâton) recevra une certaine largeur du fait que l’état a une durée de vie finie. Un tel élargissement est appelé élargissement homogène car il affecte toutes les molécules de l’ensemble de la même manière. Il y a également un élargissement en raison de petites différences dans l’environnement de chaque molécule. Ce type d’élargissement est appelé élargissement inhomogène. Indépendamment de l’origine, le modèle ci-dessus a été créé en utilisant un élargissement gaussien
Le déplacement nucléaire entre le sol et l’état excité détermine la forme du spectre d’absorption. Examinons à la fois un déplacement d’état excité plus petit et un grand déplacement d’état excité. If\(S=½\) et les surfaces d’énergie potentielle dans ce cas sont:
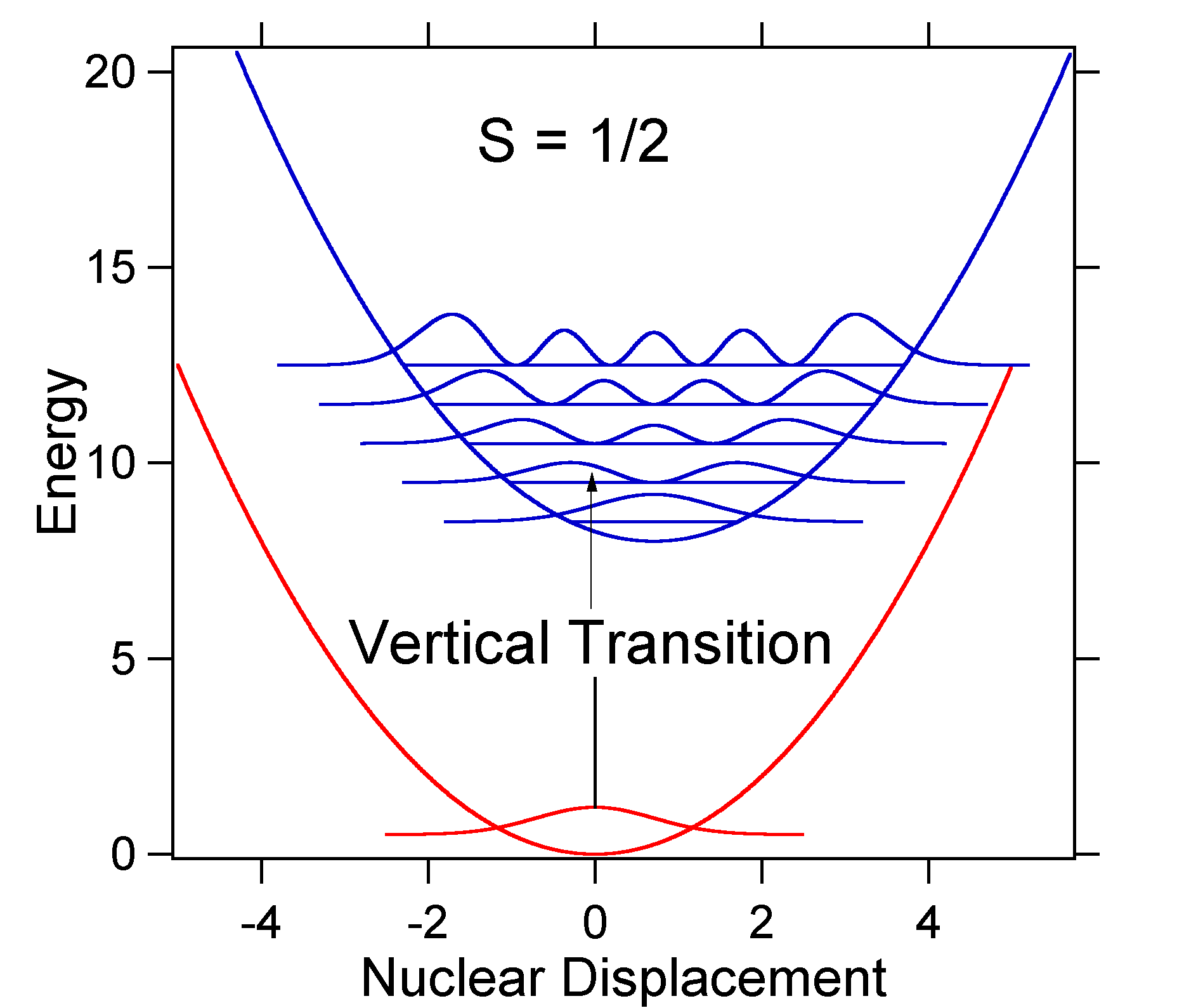
For this case the « stick » spectrum has the appearance in Figure \(\PageIndex{5}\)
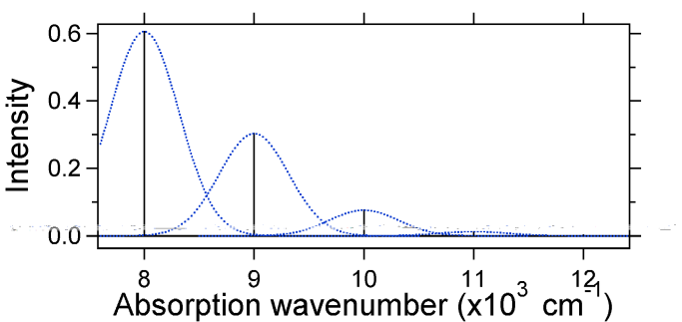
Notez que la transition vibratoire zéro-zéro ou \(S_{0,0}\) est beaucoup plus importante dans le cas où le déplacement est faible.
En règle générale, la constante \(S\) donne le rapport de l’intensité de la transition \(v = 2\) à la transition \(v = 1\). Dans ce cas puisque \(S = 0,5\), la transition \(v = 2\) est de 0,5 l’intensité de la transition \(v = 1\).
À titre d’exemple de déplacement plus important, la disposition des surfaces d’énergie potentielle pour S=2 est illustrée ci-dessous.
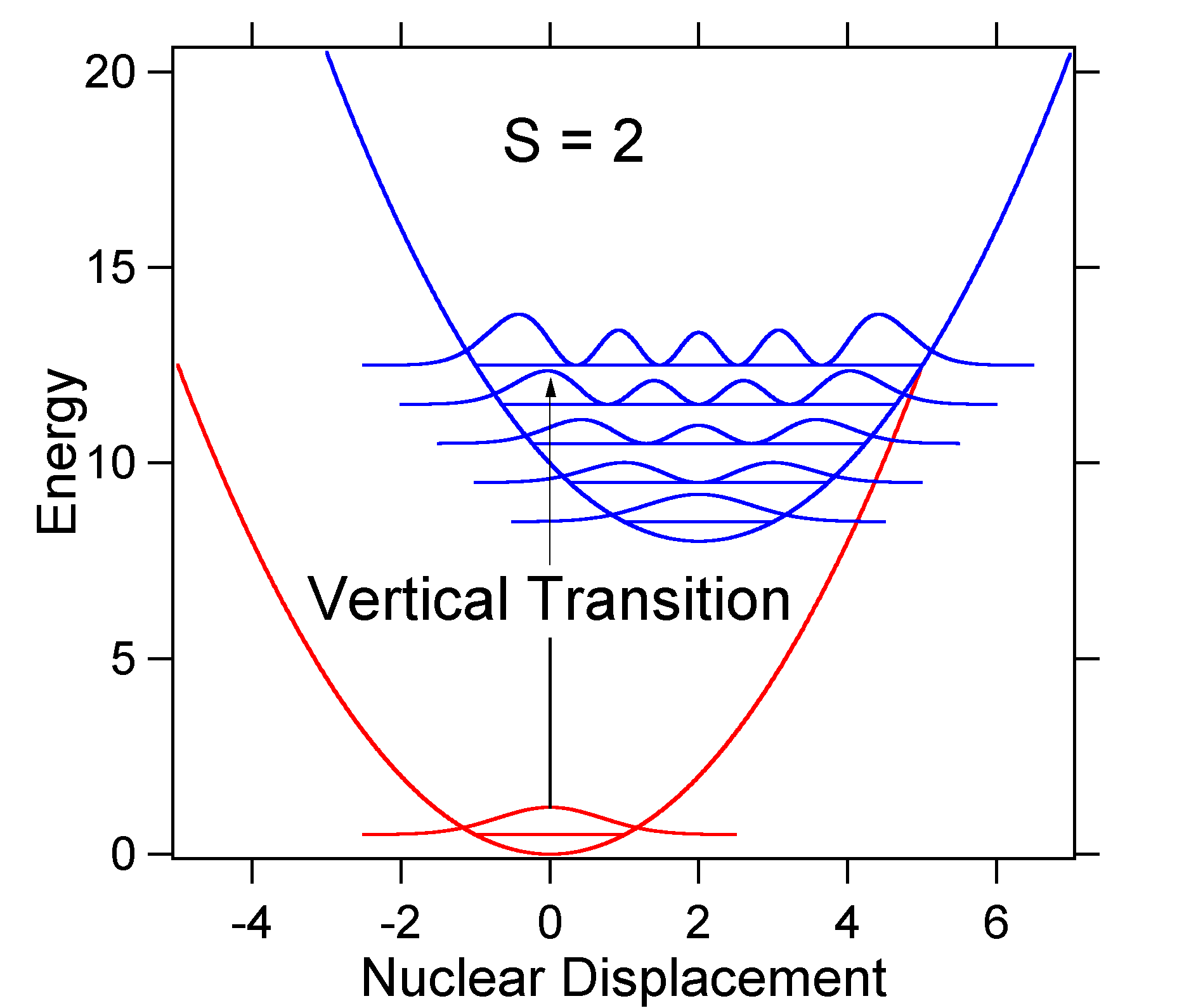
Le déplacement plus important entraîne une diminution du chevauchement du niveau d’état fondamental avec le niveau v = 0 de l’état excité. L’intensité maximale sera atteinte dans des niveaux vibratoires plus élevés, comme indiqué dans le spectre du stick.
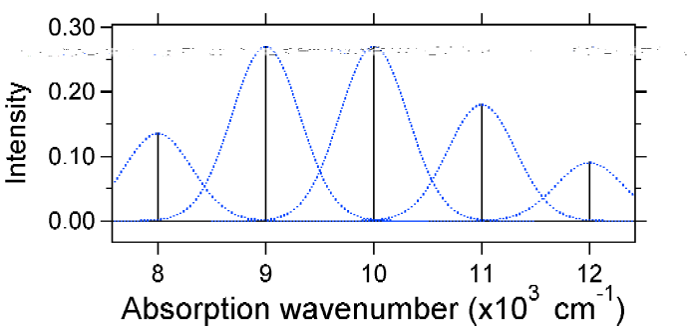
Les spectres d’absorption tracés ci-dessous ont tous la même intensité intégrée, mais leurs formes sont modifiées en raison de l’étendue différente du déplacement de la surface d’énergie potentielle de l’état excité.
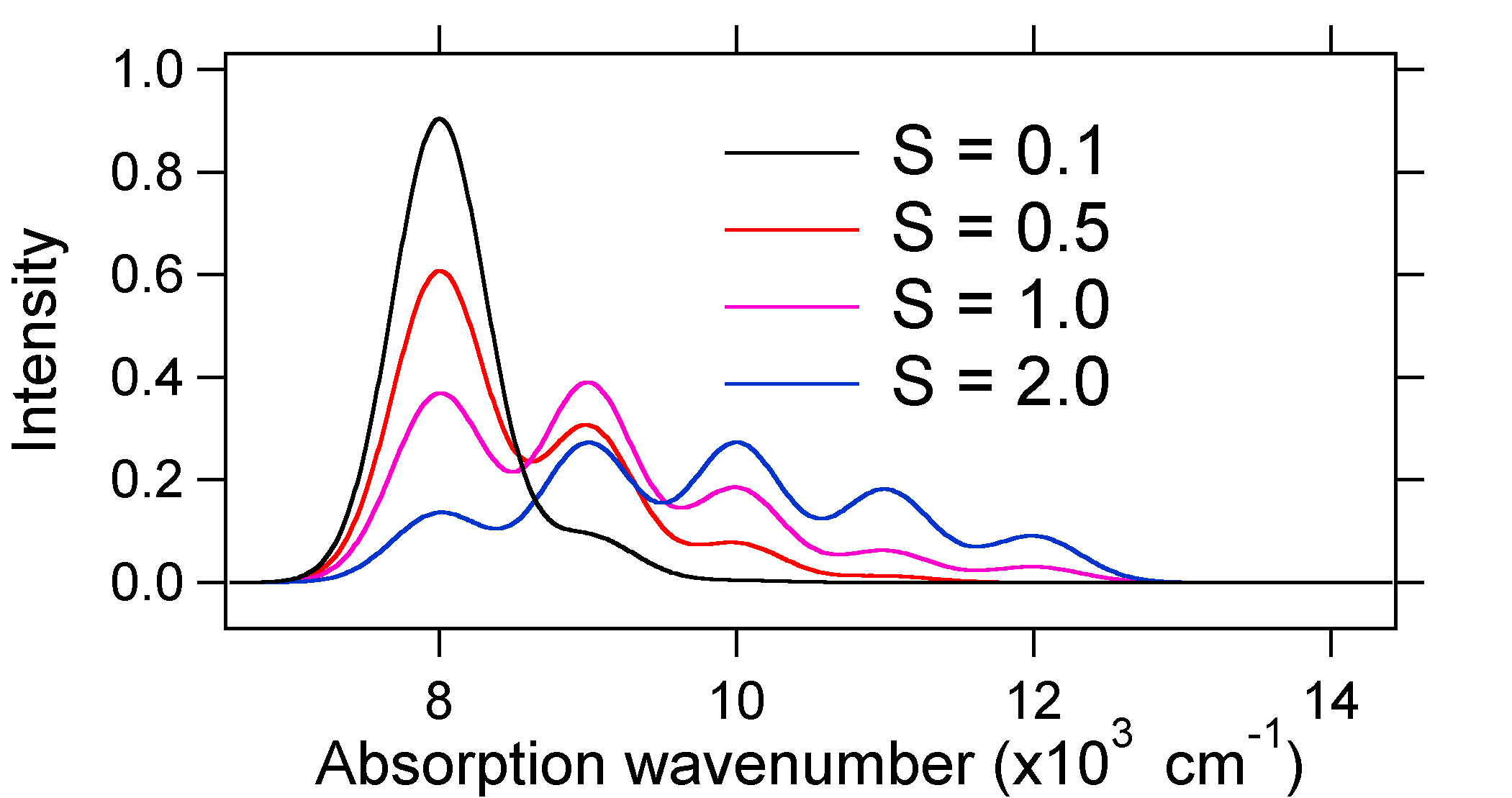
La nature des intensités de bande vibronique relative peut donc nous dire s’il y a un déplacement de la coordonnée nucléaire d’équilibre qui a accompagné une transition. Quand y aura-t-il une augmentation de la longueur de la liaison (c’est-à-dire \(Q_e > R_e\))? Cela se produit lorsqu’un électron est promu d’une orbitale moléculaire de liaison à une orbitale moléculaire sans liaison ou anti-liaison (c’est-à-dire lorsque l’ordre de liaison est moins dans l’état excité que l’état fondamental).
- Orbitale moléculaire sans liaison \(\rightarrow\)orbitale moléculaire de liaison
- Orbitale moléculaire anti-liaison \(\rightarrow\)orbitale moléculaire de liaison
- Orbitale moléculaire anti-liaison \(\rightarrow\) orbitale moléculaire sans liaison
En bref, lorsque l’ordre de liaison est plus bas à l’état excité qu’à l’état fondamental, alors \(Q_e >R_e\); une augmentation de la longueur de liaison se produira lorsque cela se produira.
- J.M. Luis, D.M. Bishop, B. Kirtman. Une approche différente pour calculer les facteurs de Franck–Condon, y compris l’anharmonicité. J. Chem. Phys., 120 (2004), p. 813 à 822.
- Atkins, Peter et Julio de Paula. Chimie physique pour les Sciences de la Vie. 2006. Il s’agit de la première édition de la série. p. 563-564
- Principe Franck-Condon. 1996, 68, 2243. Recueil de terminologie chimique de l’UICPA 2e édition (1997). www.iupac.org/goldbook/F02510.pdf
- E.Rabinowitch et Govindjee. Absorption de la lumière et Sort de l’Excitation de l’Énergie. 1969. Principe Franck-Condon. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
Contributeurs
- Matthe Zi Ziering
-
Stefan Franzen (Université d’État de Caroline du Nord)