
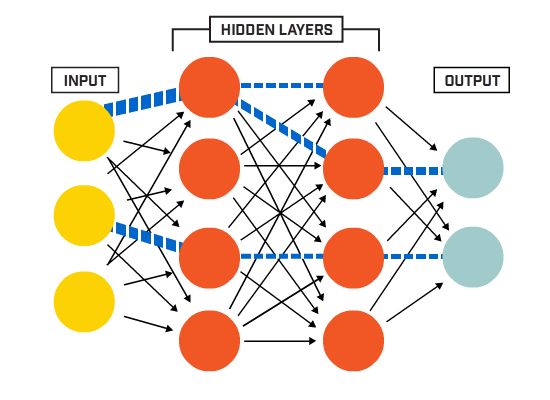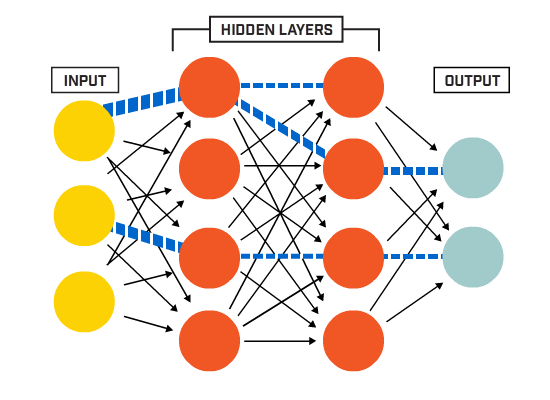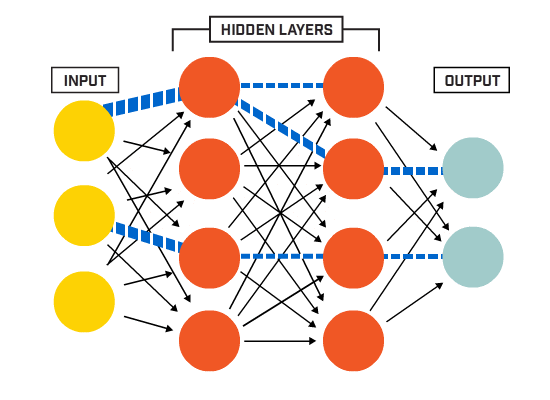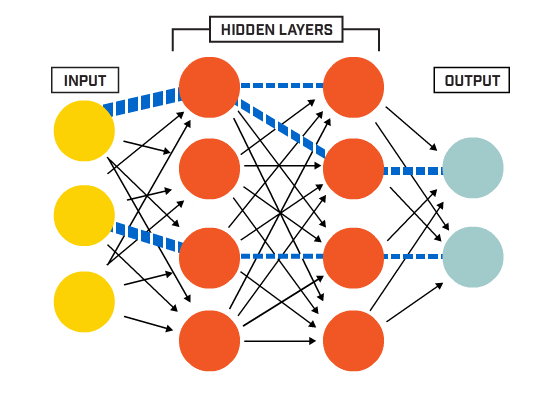
Un Réseau de Neurones Artificiels (ANN) est constitué de nombreux neurones interconnectés :
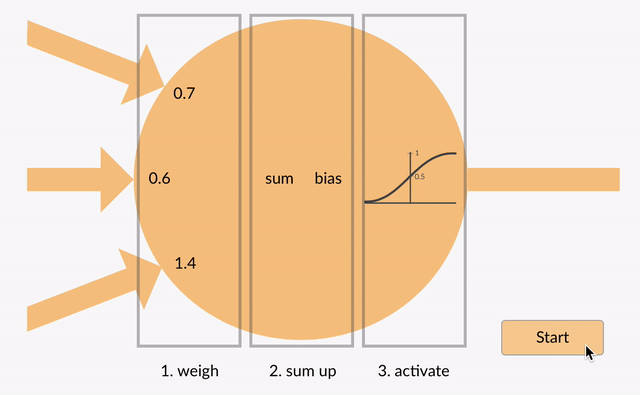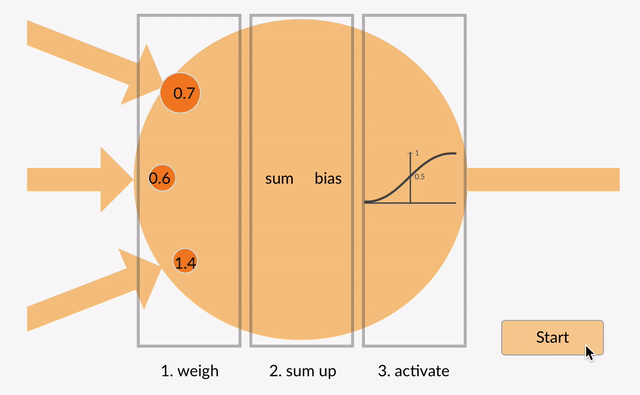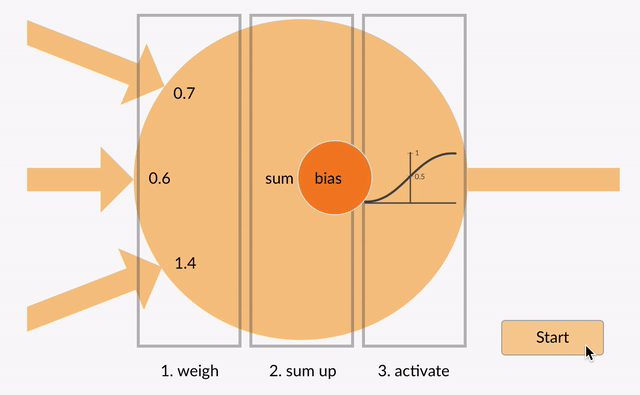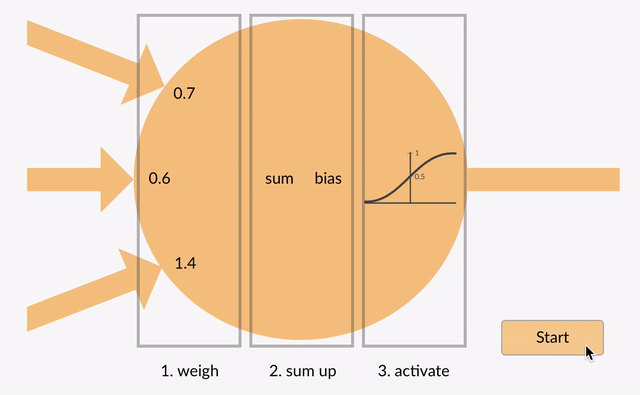
Chaque neurone prend des nombres à virgule flottante (par exemple 1,0, 0,5, -1.0) et les multiplie par d’autres nombres à virgule flottante (par exemple 0,7, 0,6, 1,4) appelés poids (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Les poids agissent comme un mécanisme pour se concentrer sur, ou ignorer, certaines entrées.

Les entrées pondérées sont ensuite additionnées (par ex. 0.7 + 0.3 + -1.4 = -0.4) avec une valeur de biais (par exemple -0,4 + -0,1 = -0,5).
La valeur sommée (x) est maintenant transformée en une valeur de sortie (y) en fonction de la fonction d’activation du neurone (y = f(x)). Certaines fonctions d’activation populaires sont présentées ci-dessous:

par exemple -0,5 → -0,05 si nous utilisons la fonction d’activation de l’Unité Linéaire Rectifiée Leaky (ReLU Leaky): y = f(x) = f(-0,5) = max(0,1 *-0,5, -0,5) = max(-0,05, -0,5) = -0.05
La valeur de sortie du neurone (par exemple -0,05) est souvent une entrée pour un autre neurone.
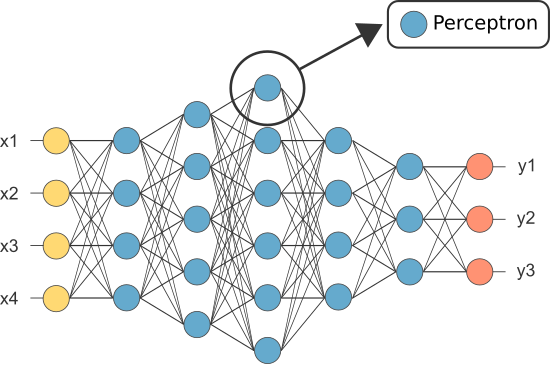
Cependant, l’un des premiers RNA était connu sous le nom de perceptron et il consistait en d’un seul neurone.

La sortie du neurone du perceptron (uniquement) agit comme prédiction finale.

Permet de coder notre propre Perceptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Remarque: nous n’avons inclus aucun algorithme d’apprentissage dans notre exemple ci—dessus – nous couvrirons les algorithmes d’apprentissage dans un autre tutoriel)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()
 div>
div>Alors pourquoi avons-nous besoin d’autant de neurones dans une ANN si l’un suffit (comme classificateur)?

Malheureusement, les neurones individuels ne sont capables de classer que des données linéairement séparables.

Cependant, en combinant les neurones ensemble, nous combinons essentiellement leurs limites de décision. Par conséquent, un ANN composé de nombreux neurones est capable d’apprendre des limites de décision complexes et non linéaires.

Les neurones sont connectés entre eux selon une architecture de réseau spécifique. Bien qu’il existe différentes architectures, presque toutes contiennent des couches. (NB: Les neurones d’une même couche ne se connectent pas entre eux)
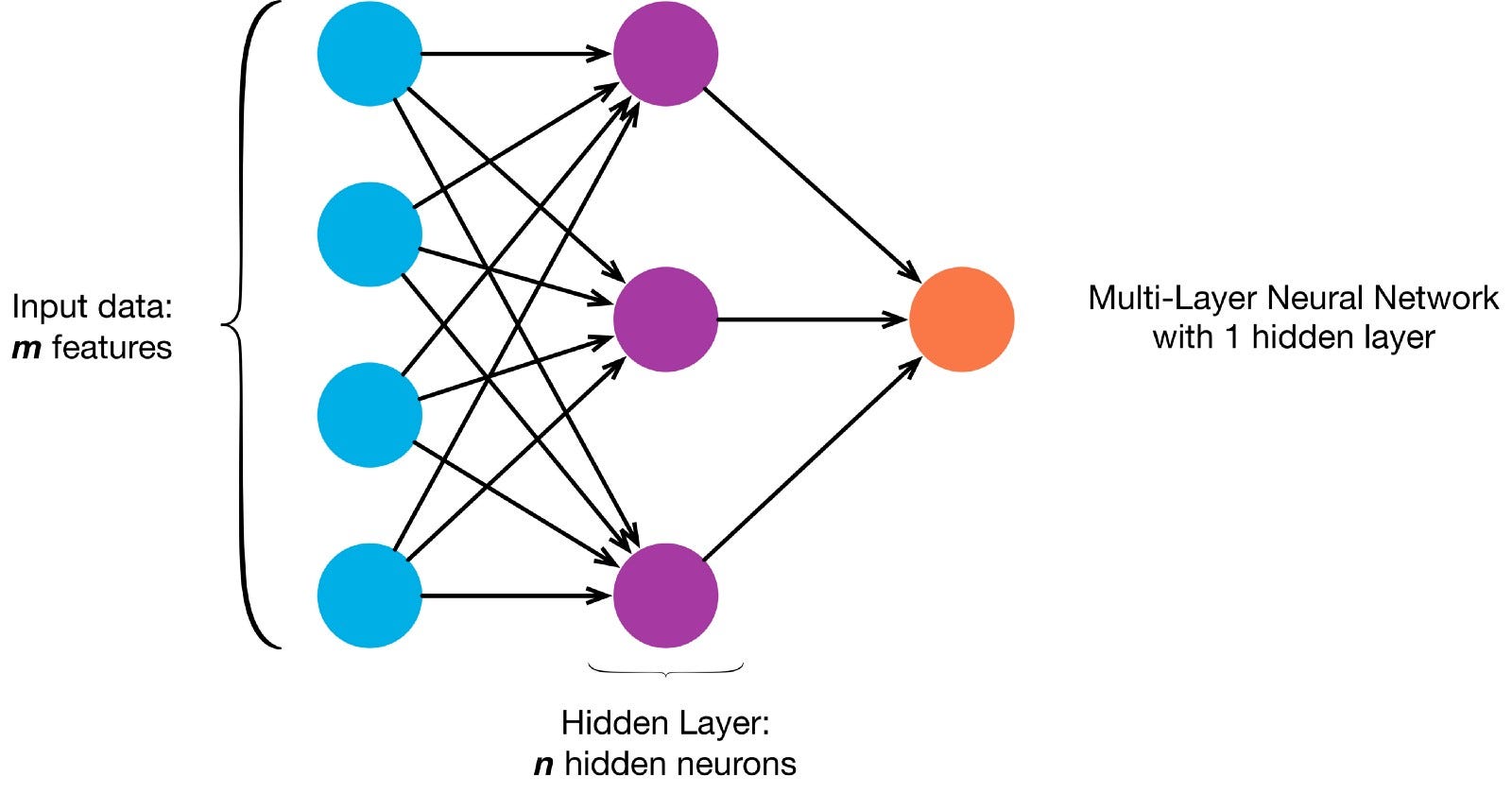
Il existe généralement une couche d’entrée (contenant un certain nombre de neurones une couche de sortie (contenant un nombre de neurones égal au nombre de classes) et une couche cachée (contenant un nombre quelconque de neurones).

Il peut y avoir plus d’une couche cachée pour permettre au réseau de neurones d’apprendre des limites de décision plus complexes (tout réseau neuronal un réseau avec plus d’une couche cachée est considéré comme un réseau neuronal profond).
Permet de construire un NN profond pour peindre cette image:

Permet de télécharger l’image et charger ses pixels dans un tableau
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
Maintenant, enseigner à notre ANN à peindre est une tâche d’apprentissage supervisée, nous devons donc créer un ensemble d’entraînement étiqueté (Nos données d’entraînement auront des entrées et des étiquettes de sortie attendues pour chaque entrée). Les entrées d’entraînement auront 2 valeurs (les coordonnées x, y de chaque pixel).
Compte tenu de la simplicité de l’image, nous pourrions en fait aborder ce problème de deux manières. Un problème de classification (où le réseau neuronal prédit si un pixel appartient à la classe « bleue » ou à la classe « grise », compte tenu de ses coordonnées xy) ou un problème de régression (où le réseau neuronal prédit des valeurs RVB pour un pixel compte tenu de ses coordonnées).
Si vous traitez cela comme un problème de régression : les sorties d’apprentissage auront 3 valeurs (les valeurs r, g, b normalisées pour chaque pixel). – Utilisons cette méthode pour l’instant.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Maintenant, créons notre ANN:

- Il devrait avoir 2 neurones dans la couche d’entrée (car il y a 2 valeurs à prendre: x & coordonnées y).
- Il devrait avoir 3 neurones dans la couche de sortie (car il y a 3 valeurs à apprendre: r, g, b).
- Le nombre de couches cachées et le nombre de neurones dans chaque couche cachée sont deux hyperparamètres à expérimenter (ainsi que le nombre d’époques pour lesquelles nous allons l’entraîner, la fonction d’activation, etc.) — J’utiliserai 10 couches cachées avec 100 neurones dans chaque couche cachée (ce qui en fait un réseau de neurones profond)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
Le réseau entraîné peut maintenant prédire les valeurs RVB normalisées pour toutes les coordonnées ( par exemple x, y = 1,1).
ann.predict(])
array(])
permet d’utiliser l’ANN pour prédire les valeurs rvb pour chaque coordonnée et permet d’afficher les valeurs rvb prédites pour l’image entière pour voir à quel point cela s’est bien passé (qualitativement — nous laisserons les métriques d’évaluation pour un autre tutoriel)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

Essayez de changer les hyperparamètres pour obtenir de meilleurs résultats.
Si au lieu de traiter cela comme un problème de régression, nous traitons cela comme un problème de classification, alors les sorties d’apprentissage auront 2 valeurs (les probabilités du pixel appartenant à chacune des deux classes: « bleu » et « gris »)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
Nous pouvons reconstruire notre ANN en tant que classificateur binaire avec 2 neurones dans la couche d’entrée, 2 neurones dans la couche de sortie et 100 neurones dans la couche cachée (avec 10 couches cachées)
p>
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
Nous pouvons maintenant utiliser l’ANN entraîné pour prédire la classe à laquelle chaque pixel appartient (0: « gris » ou 1: »bleu »). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: « grey »)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

