Comprendre les réseaux résiduels profonds

Les réseaux résiduels profonds (ResNet) ont pris d’assaut le monde de l’apprentissage profond lorsque Microsoft Research a publié l’apprentissage résiduel profond pour la reconnaissance d’images. Ces réseaux ont permis de remporter la 1ère place dans les cinq volets principaux des concours ImageNet et COCO 2015, qui couvraient la classification des images, la détection des objets et la segmentation sémantique. La robustesse des ResNets a depuis été prouvée par diverses tâches de reconnaissance visuelle et par des tâches non visuelles impliquant la parole et le langage. J’ai également utilisé ResNet en plus d’autres modèles d’apprentissage profond dans ma recherche de thèse de doctorat.

Cet article résumera les trois articles ci-dessous, qui sont tous écrits ou co-écrits par l’inventeur de ResNet, Kaiming He, car je crois que les articles originaux donnent l’explication la plus intuitive et la plus détaillée du modèle / des réseaux. Espérons que cet article pourrait vous aider à mieux comprendre l’essentiel des réseaux résiduels.

• Apprentissage Résiduel Profond pour la Reconnaissance d’Image
• Mappages d’identité dans les Réseaux Résiduels Profonds
• Transformation Résiduelle Agrégée pour les Réseaux Neuronaux Profonds

Intuition sur un Réseau Résiduel Profond (référence stackoverflow)

Un bloc résiduel est affiché comme suit :

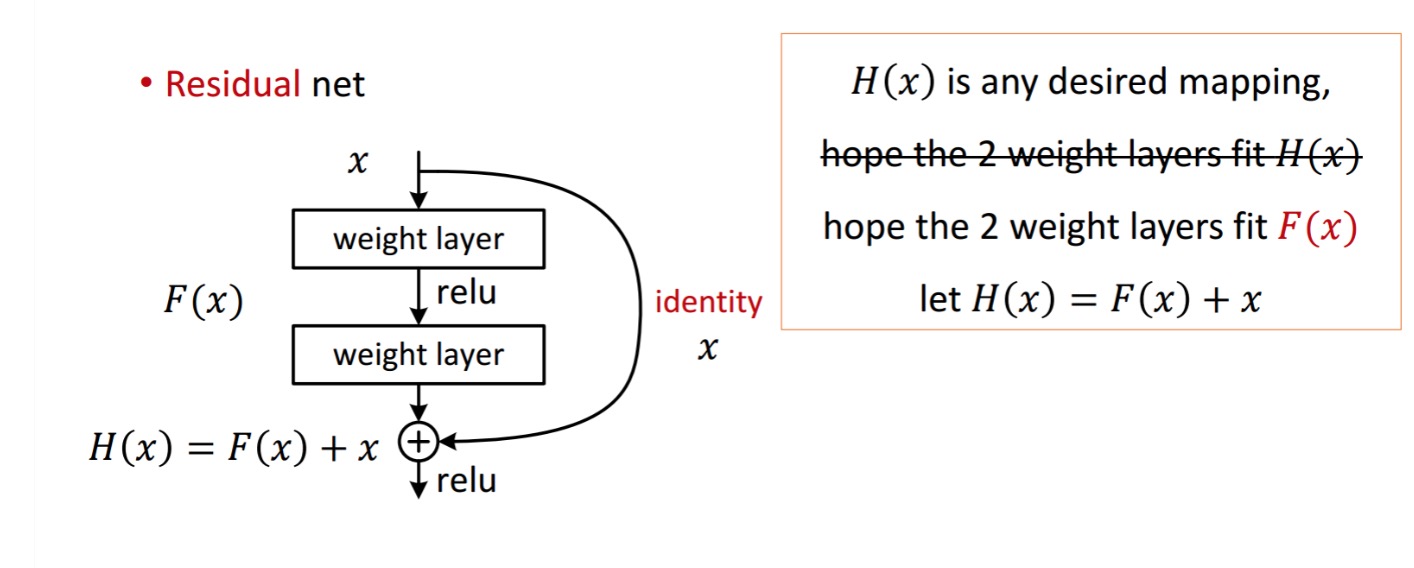
Ainsi, l’unité résiduelle représentée est obtenue par traitement avec deux couches de poids. Ensuite, il ajoute à pour obtenir. Maintenant, supposons que c’est votre sortie prévue idéale qui correspond à votre vérité au sol. Depuis, l’obtention du désiré dépend de l’obtention du parfait. Cela signifie que les deux couches de poids de l’unité résiduelle devraient en fait pouvoir produire le résultat souhaité, puis obtenir l’idéal est garanti.

est obtenu de la manière suivante.

est obtenu de la manière suivante.

Les auteurs émettent l’hypothèse que la cartographie résiduelle (c’est-à-dire) peut être plus facile à optimiser que. Pour illustrer avec un exemple simple, supposons que l’idéal. Ensuite, pour un mappage direct, il serait difficile d’apprendre un mappage d’identité car il existe une pile de couches non linéaires comme suit.

Il serait donc difficile d’approximer la cartographie d’identité avec tous ces poids et ReLUs au milieu.

Maintenant, si nous définissons le mappage souhaité, nous avons juste besoin de get comme suit.

La réalisation de ce qui précède est facile. Il suffit de mettre n’importe quel poids à zéro et vous obtiendrez une sortie nulle. Ajoutez de nouveau et vous obtenez le mappage souhaité.

Apprentissage Résiduel profond pour la reconnaissance d’images

Problème

Lorsque des réseaux plus profonds commencent à converger, un problème de dégradation a été exposé: avec l’augmentation de la profondeur du réseau, la précision est saturée puis se dégrade rapidement.

Voir la dégradation en action:

Prenons un réseau peu profond et son homologue plus profond en y ajoutant plus de couches.

Pire scénario: Les premières couches du modèle Deeper peuvent être remplacées par un réseau peu profond et les couches restantes peuvent simplement agir comme une fonction d’identité (entrée égale à la sortie).

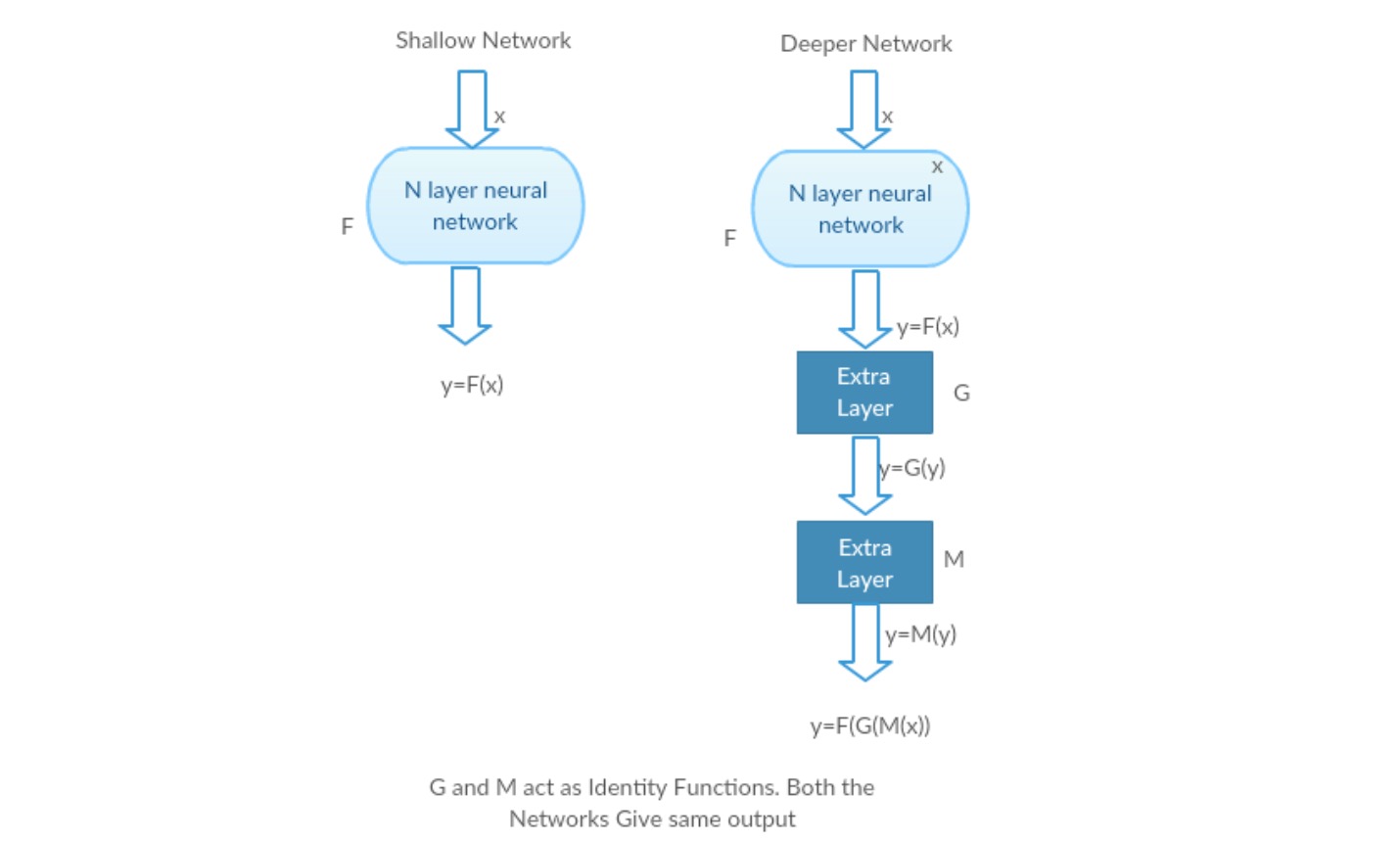
Scénario gratifiant: Dans le réseau plus profond, les couches supplémentaires se rapprochent mieux du mappage que sa partie compteur moins profonde et réduisent l’erreur d’une marge significative.

Expérience: Dans le pire des cas, le réseau peu profond et sa variante plus profonde devraient donner la même précision. Dans le cas du scénario gratifiant, le modèle plus profond devrait donner une meilleure précision que sa contre-pièce moins profonde. Mais les expériences avec nos solveurs actuels révèlent que les modèles plus profonds ne fonctionnent pas bien. L’utilisation de réseaux plus profonds dégrade donc les performances du modèle. Ces articles tentent de résoudre ce problème en utilisant un cadre d’apprentissage résiduel profond.

Comment résoudre?

Au lieu d’apprendre un mappage direct de avec une fonction (quelques couches non linéaires empilées). Définissons la fonction résiduelle en utilisant, qui peut être recadrée en, où et représente les couches non linéaires empilées et la fonction d’identité (entrée = sortie) respectivement.

L’hypothèse de l’auteur est qu’il est facile d’optimiser la fonction de mappage résiduel plutôt que d’optimiser le mappage original non référencé.

Intuition derrière les blocs résiduels :

Prenons l’exemple du mappage d’identité (par exemple). Si le mappage d’identité est optimal, nous pouvons facilement pousser les résidus à zéro() plutôt que d’adapter un mappage d’identité () par une pile de couches non linéaires. Dans un langage simple, il est très facile de trouver une solution comme plutôt que d’utiliser une pile de couches cnn non linéaires comme fonction (pensez-y). Donc, cette fonction est ce que les auteurs ont appelé la fonction résiduelle.

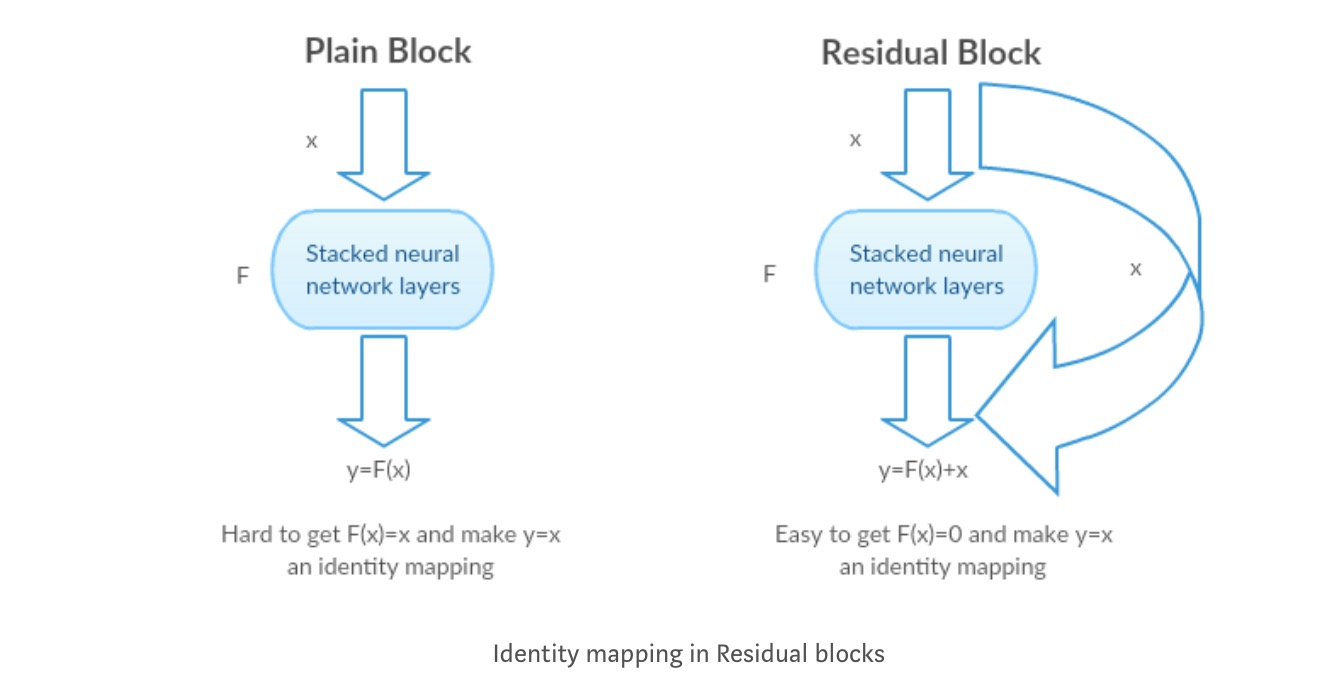
Les auteurs ont effectué plusieurs tests pour tester leur hypothèse. Regardons chacun d’eux maintenant.

Cas de test:

Prenez un réseau simple (réseau à 18 couches de type VGG) (Réseau-1) et une variante plus profonde de celui-ci (34 couches, Réseau-2) et ajoutez des couches résiduelles au Réseau-2 (34 couches avec des connexions résiduelles, Réseau-3).

Conception du réseau:

1. Utilisez principalement 3 *3 filtres.
2. Échantillonnage descendant avec des couches CNN avec stride 2.
3. Couche de mise en commun moyenne globale et une couche entièrement connectée à 1000 voies avec Softmax à la fin.

Il existe deux types de connexions résiduelles :

I. Les raccourcis d’identité() peuvent être directement utilisés lorsque l’entrée() et la sortie() sont de mêmes dimensions.

II. Lorsque les dimensions changent, A) Le raccourci effectue toujours un mappage d’identité, avec des entrées zéro supplémentaires complétées avec la dimension augmentée. B) Le raccourci de projection est utilisé pour faire correspondre la dimension (fait par 1 * 1 conv) en utilisant la formule suivante

Résultats

Même si le réseau à 18 couches n’est que le sous-espace du réseau à 34 couches, il fonctionne toujours mieux. ResNet surpasse d’une marge significative dans le cas où le réseau est plus profond

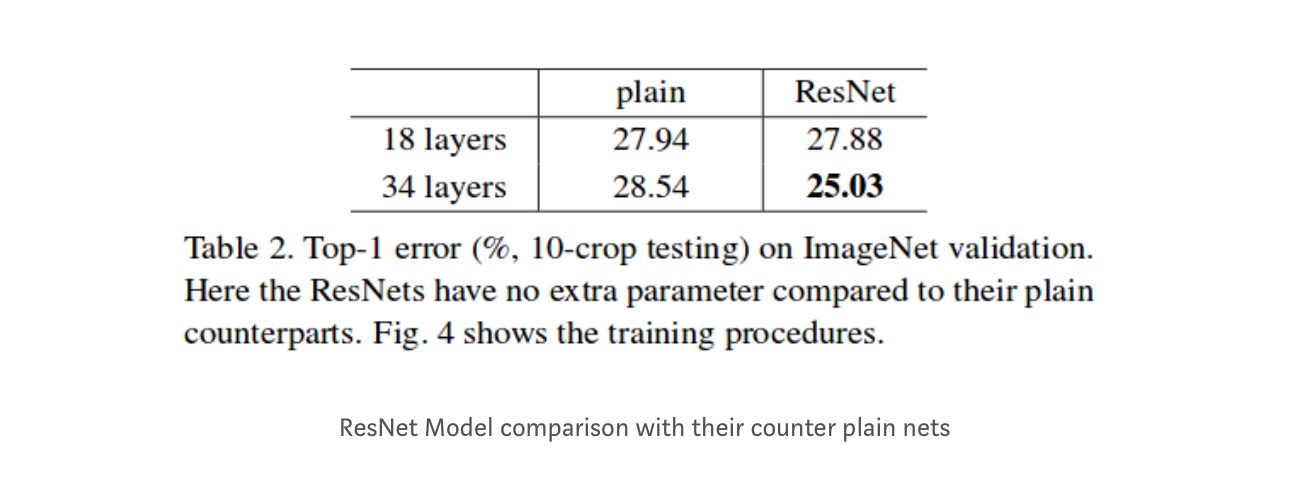
Études plus approfondies

De plus, plus de réseaux sont étudiés :

Chaque bloc ResNet est soit à 2 couches de profondeur (utilisé dans les petits réseaux comme ResNet 18, 34) ou 3 couches profondes (ResNet 50, 101, 152).

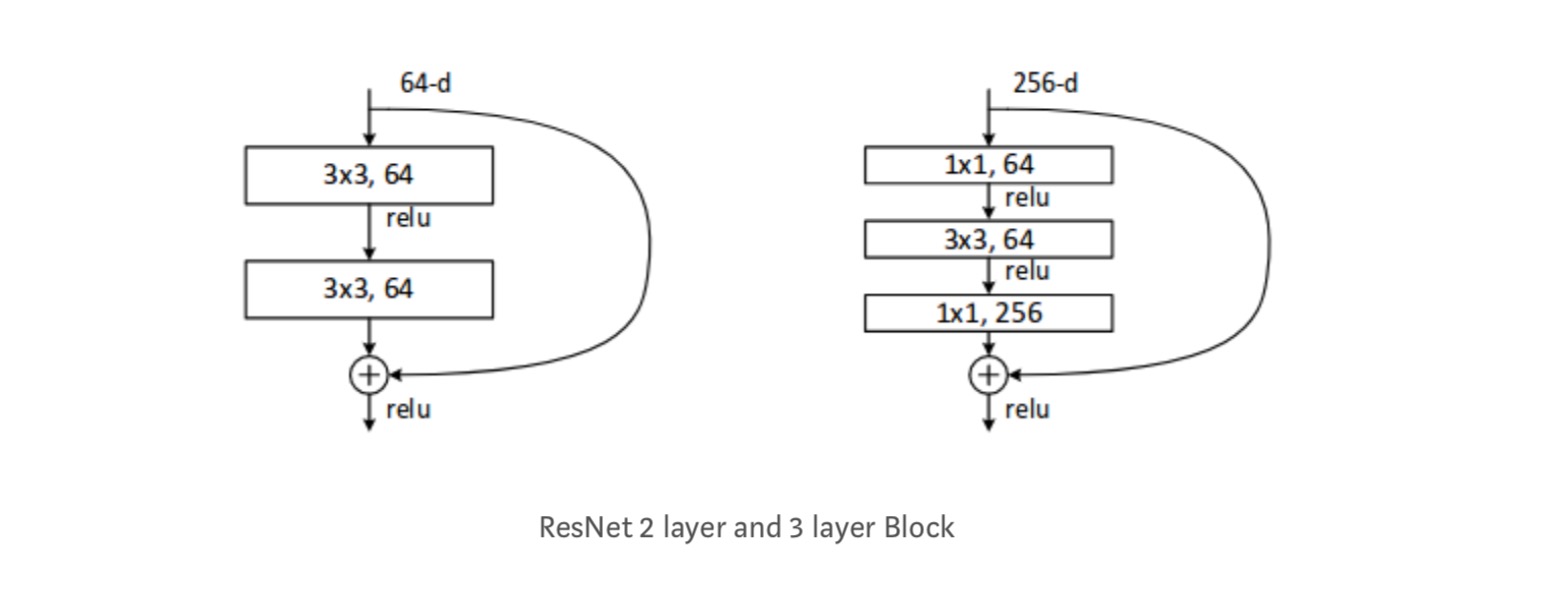
Observations

1. Le réseau ResNet Converge plus rapidement par rapport à une partie simple de celui-ci.
2. Identité vs shorcuts de projection. De très petits gains incrémentiels à l’aide de raccourcis de projection (Équation-2) dans toutes les couches. Ainsi, tous les blocs ResNet utilisent uniquement des raccourcis d’identité avec des raccourcis de projections utilisés uniquement lorsque les dimensions changent.
3. ResNet-34 a obtenu une erreur de validation top-5 de 5,71% de mieux que BN-inception et VGG. ResNet-152 atteint une erreur de validation top-5 de 4,49%. Un ensemble de 6 modèles avec des profondeurs différentes atteint une erreur de validation top-5 de 3,57%. Gagner la 1ère place dans ILSVRC-2015

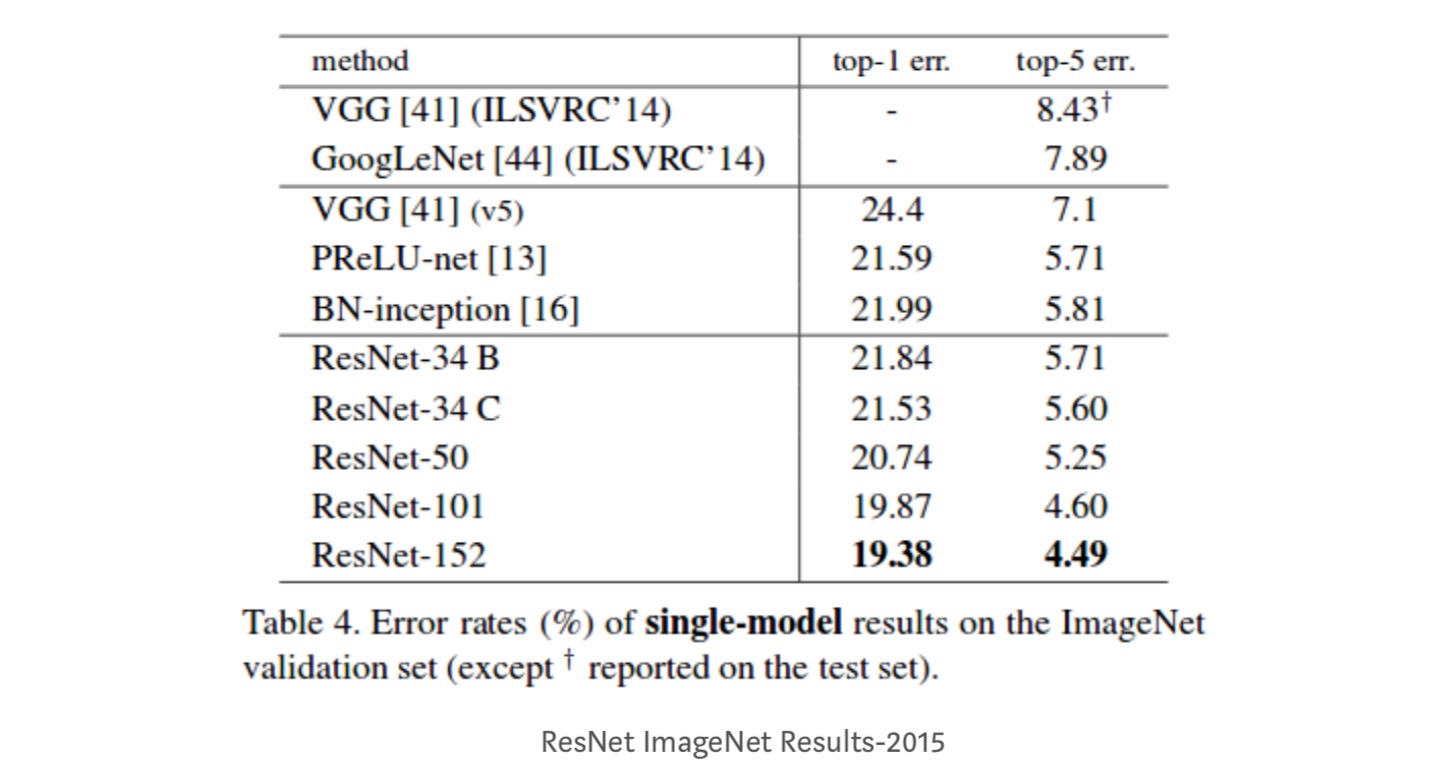
Mappages d’identité dans les réseaux résiduels profonds

Cet article donne la compréhension théorique des raisons pour lesquelles le problème de gradient de fuite n’est pas présent dans les réseaux résiduels et du rôle des connexions de saut (les connexions de saut signifient l’entrée ou) en remplaçant le mappage d’identité (x) par différentes fonctions.

Introduction

Les réseaux résiduels profonds sont constitués de nombreuses « unités résiduelles » empilées. Chaque unité peut être exprimée sous une forme générale:

où et sont l’entrée et la sortie de l’unité, et est une fonction résiduelle. Dans le dernier article, est un mappage d’identité et est une fonction ReLU.

L’idée centrale des ResNets est d’apprendre la fonction résiduelle additive par rapport à, avec un choix clé d’utilisation d’un mappage d’identité. Ceci est réalisé en attachant une connexion de saut d’identité (« raccourci »).

Dans cet article, nous analysons les réseaux résiduels profonds en nous concentrant sur la création d’un chemin « direct » pour propager l’information — non seulement au sein d’une unité résiduelle, mais à travers l’ensemble du réseau. Nos dérivations révèlent que si les deux et sont des mappages d’identité, le signal pourrait être directement propagé d’une unité à n’importe quelle autre unité, dans les passes avant et arrière. Nos expériences montrent empiriquement que la formation en général devient plus facile lorsque l’architecture est plus proche des deux conditions ci-dessus.

Pour comprendre le rôle des connexions de saut, nous analysons et comparons différents types de. Nous constatons que le mappage d’identité choisi dans le dernier article permet la réduction d’erreur la plus rapide et la perte d’entraînement la plus faible parmi toutes les variantes que nous avons étudiées, tandis que les connexions de saut de mise à l’échelle, de déclenchement et de circonvolutions 1 × 1 entraînent toutes des pertes et des erreurs d’entraînement plus élevées. Ces expériences suggèrent que le maintien d’un chemin d’information « propre » est utile pour faciliter l’optimisation.

Pour construire un mappage d’identité, nous considérons les fonctions d’activation (ReLU et BN) comme une « pré-activation » des couches de poids, contrairement à la sagesse conventionnelle de la « post-activation ». Ce point de vue conduit à une nouvelle conception d’unité résiduelle, illustrée sur la figure suivante. Sur la base de cette unité, nous présentons des résultats compétitifs sur CIFAR-10/100 avec un ResNet à 1001 couches, beaucoup plus facile à former et généralisant mieux que le ResNet d’origine. Nous rapportons également des résultats améliorés sur ImageNet en utilisant un ResNet de 200 couches, pour lequel la contrepartie du dernier papier commence à surajuster. Ces résultats suggèrent qu’il y a beaucoup de place pour exploiter la dimension de la profondeur du réseau, une clé du succès de l’apprentissage profond moderne.

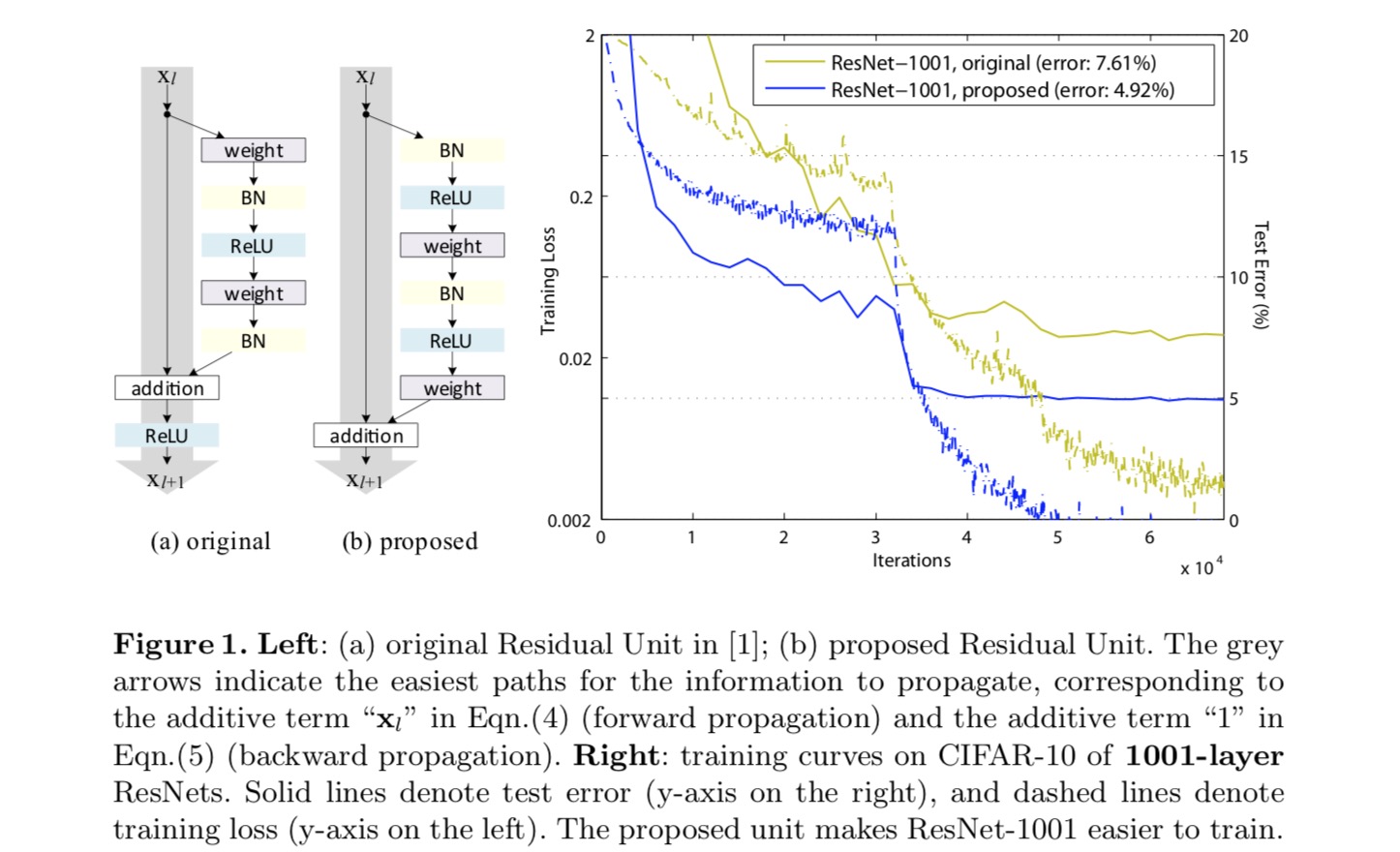
Analyse des réseaux résiduels profonds

Les ResNets développés dans le dernier article sont des architectures modularisées qui empilent des blocs de construction de la même forme de connexion. Dans cet article, nous appelons ces blocs des « Unités résiduelles ». L’unité résiduelle d’origine dans le dernier article effectue le calcul suivant:

Voici la fonction d’entrée de la -th unité résiduelle. est un ensemble de poids (et de biais) associés à la -th Unité Résiduelle, et est le nombre de couches dans une Unité Résiduelle (est 2 ou 3 dans le dernier papier). désigne la fonction résiduelle, e.g., une pile de deux couches convolutives 3×3 dans le dernier papier. La fonction est l’opération après addition par élément, et dans le dernier article est ReLU. La fonction est définie comme un mappage d’identité : .

Si est aussi un mappage d’identité :, nous pouvons obtenir :

Récursivement nous aurons :

pour toute unité plus profonde et toute unité moins profonde. Cette équation présente quelques belles propriétés. (1) La caractéristique de toute unité plus profonde peut être représentée comme la caractéristique de toute unité moins profonde plus une fonction résiduelle sous une forme de, indiquant que le modèle est de manière résiduelle entre toutes les unités et. (2) La caractéristique, de toute unité profonde, est la somme des sorties de toutes les fonctions résiduelles précédentes (plus). Cela contraste avec un « réseau simple » où une caractéristique est une série de produits vectoriels matriciels, par exemple (en ignorant BN et ReLU).

L’équation ci-dessus conduit également à de belles propriétés de propagation vers l’arrière. Désignant la fonction de perte comme, à partir de la règle de chaîne de rétropropagation, nous avons:

L’équation ci-dessus indique que le gradient peut être décomposé en deux termes additifs: un terme de qui propage des informations directement sans concerner aucune couche de poids, et un autre terme de qui se propage à travers les couches de poids. Le terme additif de garantit que l’information est directement propagée à toute unité moins profonde l. L’équation ci-dessus suggère également qu’il est peu probable que le gradient soit annulé pour un mini-lot, car en général, le terme ne peut pas toujours être -1 pour tous les échantillons d’un mini-lot. Cela implique que le gradient d’une couche ne disparaît pas même lorsque les poids sont arbitrairement faibles.

Les deux équations ci-dessus suggèrent que le signal peut être directement propagé de n’importe quelle unité à une autre, à la fois vers l’avant et vers l’arrière. La base des deux premières équations ci-dessus est deux mappages d’identité: (1) la connexion de saut d’identité et (2) la condition qui est un mappage d’identité.

Importance des connexions de saut d’identité

Considérons une simple modification,, pour casser le raccourci d’identité:

où est un scalaire modulant (pour plus de simplicité, nous supposons toujours que c’est l’identité). En appliquant récursivement cette formulation, nous obtenons une équation similaire à celle ci-dessus:

où la notation absorbe les scalaires dans les fonctions résiduelles. De même, nous avons une rétropropagation de la forme suivante:

Contrairement à l’équation précédente, dans cette équation, le premier terme additif est modulé par un facteur. Pour un réseau extrêmement profond (est grand), si pour tous, ce facteur peut être exponentiellement grand; si pour tous, ce facteur peut être exponentiellement petit et disparaître, ce qui bloque le signal rétropropagué du raccourci et le force à circuler à travers les couches de poids. Il en résulte des difficultés d’optimisation comme nous le montrons par des expériences.

Dans l’analyse ci-dessus, la connexion de saut d’identité d’origine est remplacée par une simple mise à l’échelle. Si la connexion de saut représente des transformées plus compliquées (telles que la commutation et les circonvolutions 1 × 1), dans l’équation ci-dessus, le premier terme devient où est la dérivée de. Ce produit peut également entraver la propagation de l’information et entraver la procédure de formation, comme en témoignent les expériences suivantes.

Expériences sur les connexions de saut

Nous expérimentons avec le ResNet à 110 couches sur CIFAR-10. Ce ResNet-110 extrêmement profond possède 54 unités résiduelles à deux couches (composées de 3×3 couches convolutives) et est difficile à optimiser. Différents types de connexions de saut sont expérimentées. Voir la figure suivante :

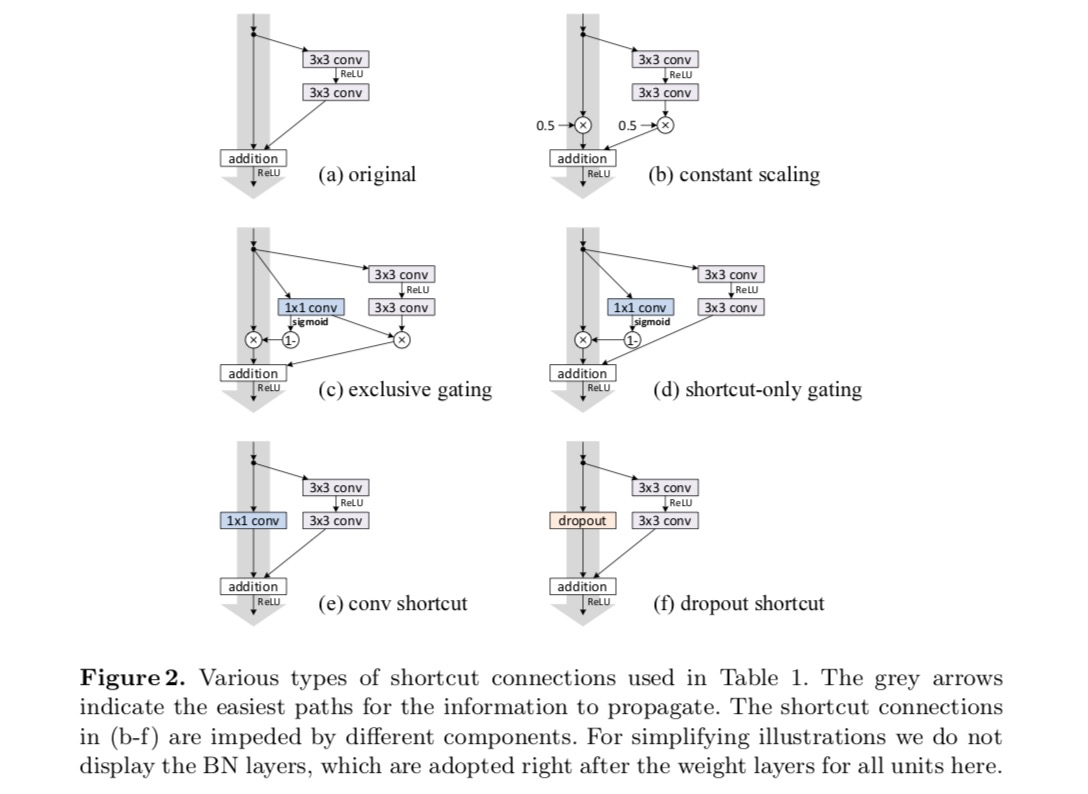
Les résultats de la classification sont affichés dans le tableau suivant :

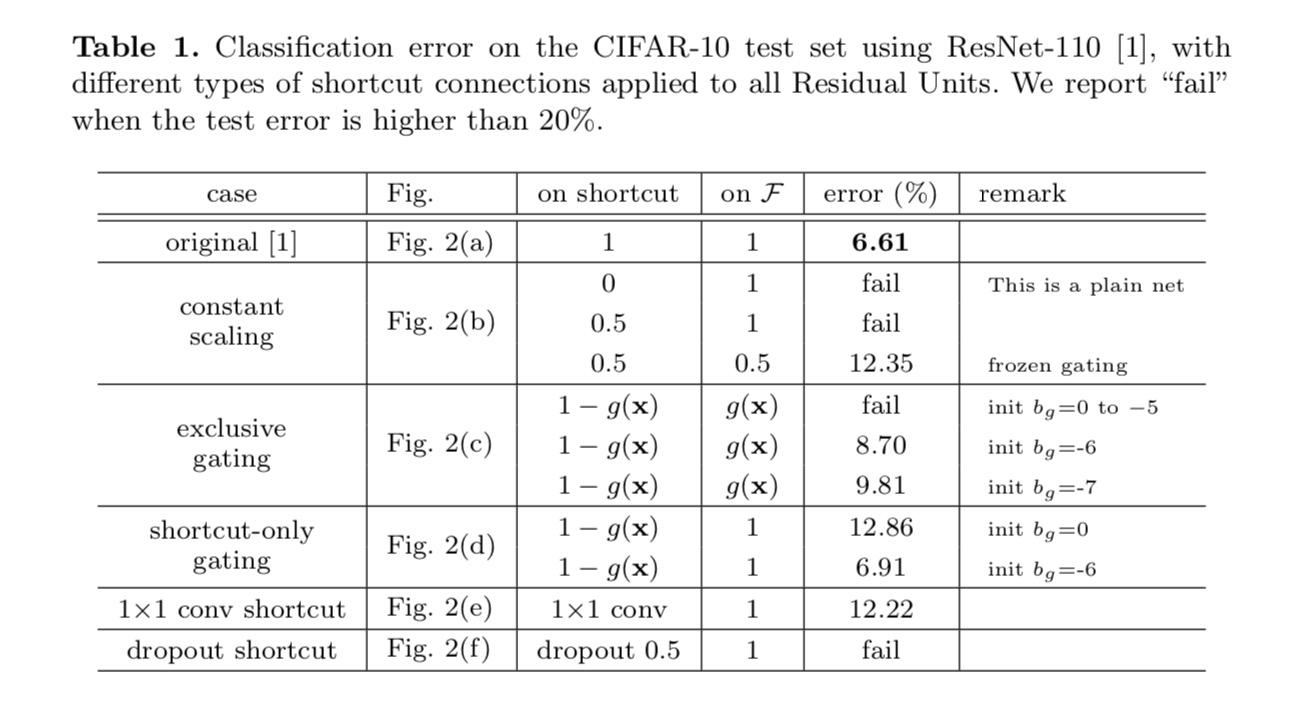
Comme l’indiquent les flèches grises de la figure ci-dessus, les connexions de raccourci sont les chemins les plus directs pour la propagation de l’information. Les manipulations multiplicatives (mise à l’échelle, gating, circonvolutions 1×1 et abandon) sur les raccourcis peuvent entraver la propagation de l’information et entraîner des problèmes d’optimisation.

Il est à noter que les raccourcis de commutation et de convolution 1×1 introduisent plus de paramètres et devraient avoir des capacités de représentation plus fortes que les raccourcis d’identité. En fait, le gating réservé aux raccourcis et la convolution 1× 1 couvrent l’espace de solution des raccourcis d’identité (c’est-à-dire qu’ils pourraient être optimisés en tant que raccourcis d’identité). Cependant, leur erreur d’apprentissage est plus élevée que celle des raccourcis d’identité, ce qui indique que la dégradation de ces modèles est causée par des problèmes d’optimisation, au lieu de capacités de représentation.

Utilisation des fonctions d’activation

Les expériences dans la section ci-dessus supposent que l’activation après addition est le mappage d’identité. Mais dans les expériences ci-dessus est ReLU tel que conçu dans le premier article. Ensuite, nous étudions l’impact de.

Nous voulons faire un mappage d’identité, qui se fait en réorganisant les fonctions d’activation (ReLU et/ou BN, normalisation par lots). Dans la figure suivante, l’unité résiduelle d’origine dans le dernier papier a une forme dans la Fig. 4(a)-BN est utilisé après chaque couche de poids, et ReLU est adopté après BN, sauf que le dernier ReLU d’une unité résiduelle est après l’addition élément par élément (= ReLU). Figue. 4 (b-e) montrez les alternatives que nous avons étudiées.

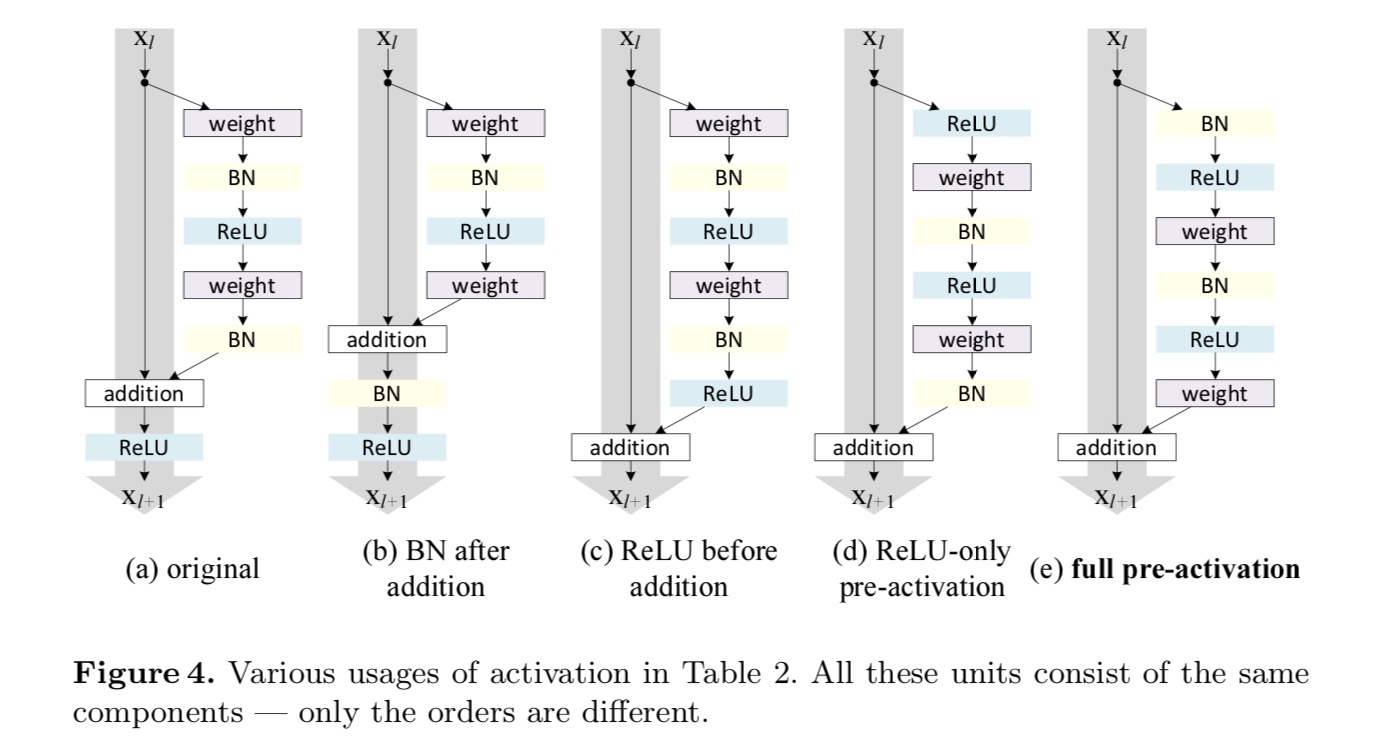
Expériences sur l’activation

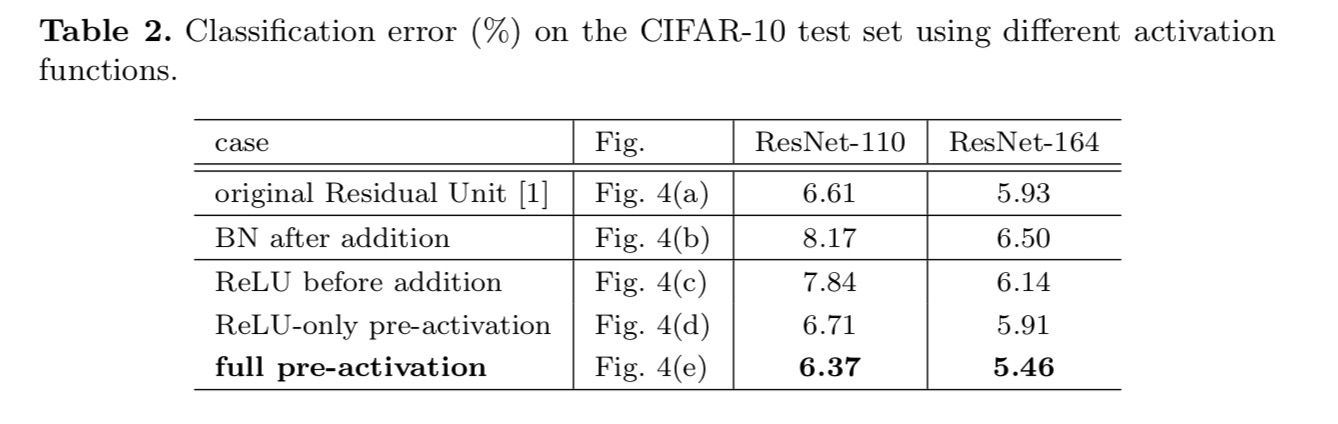
Dans cette section, nous expérimentons avec ResNet-110 et une architecture de goulot d’étranglement à 164 couches (notée ResNet-164). Une unité résiduelle de goulot d’étranglement se compose d’une couche 1× 1 pour réduire la dimension, d’une couche 3×3 et d’une couche 1× 1 pour restaurer la dimension. Comme conçu dans le dernier article, sa complexité de calcul est similaire à l’unité résiduelle à deux – 3×3.

Post-activation ou pré-activation?

Dans la conception d’origine, l’activation affecte les deux chemins de l’unité résiduelle suivante: . Ensuite, nous développons une forme asymétrique où une activation n’affecte que le chemin:, pour tout. En renommant les notations, on a la forme suivante :

Pour cette nouvelle Unité résiduelle comme dans l’équation ci-dessus, la nouvelle activation après addition devient un mappage d’identité. Cette conception signifie que si une nouvelle activation après addition est adoptée de manière asymétrique, cela équivaut à une refonte en tant que préactivation de l’unité résiduelle suivante. Ceci est illustré dans la figure suivante:

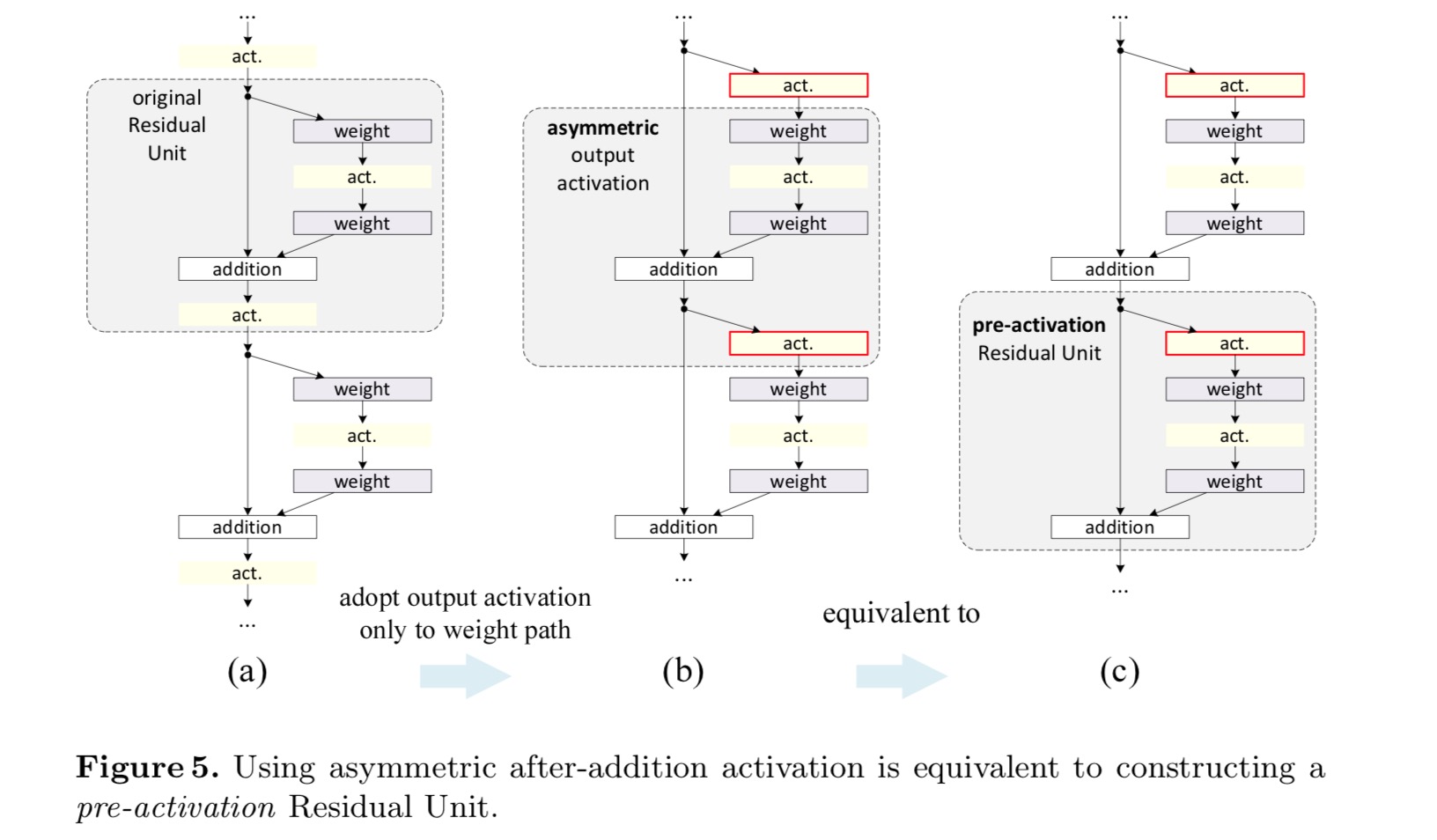
La distinction entre post-activation / pré-activation est causée par la présence de l’addition par élément. Pour un réseau simple qui a N couches, il y a N-1 activations (BN /ReLU), et peu importe que nous les considérions comme des post- ou des pré-activations. Mais pour les couches ramifiées fusionnées par addition, la position d’activation compte. Les différents usages d’activation sont représentés sur la figure 4.

Nous expérimentons avec deux de ces conceptions: (1) Pré-activation ReLU uniquement et (2) pré-activation complète où BN et ReLU sont tous deux adoptés avant les couches de poids. D’une manière surprenante, lorsque BN et ReLU sont tous deux utilisés comme pré-activation, les résultats sont améliorés par des marges saines

Nous constatons que l’impact de la pré-activation est double. Tout d’abord, l’optimisation est encore facilitée (par rapport au ResNet de base) car f est un mappage d’identité. Deuxièmement, l’utilisation de BN comme pré-activation améliore la régularisation des modèles.

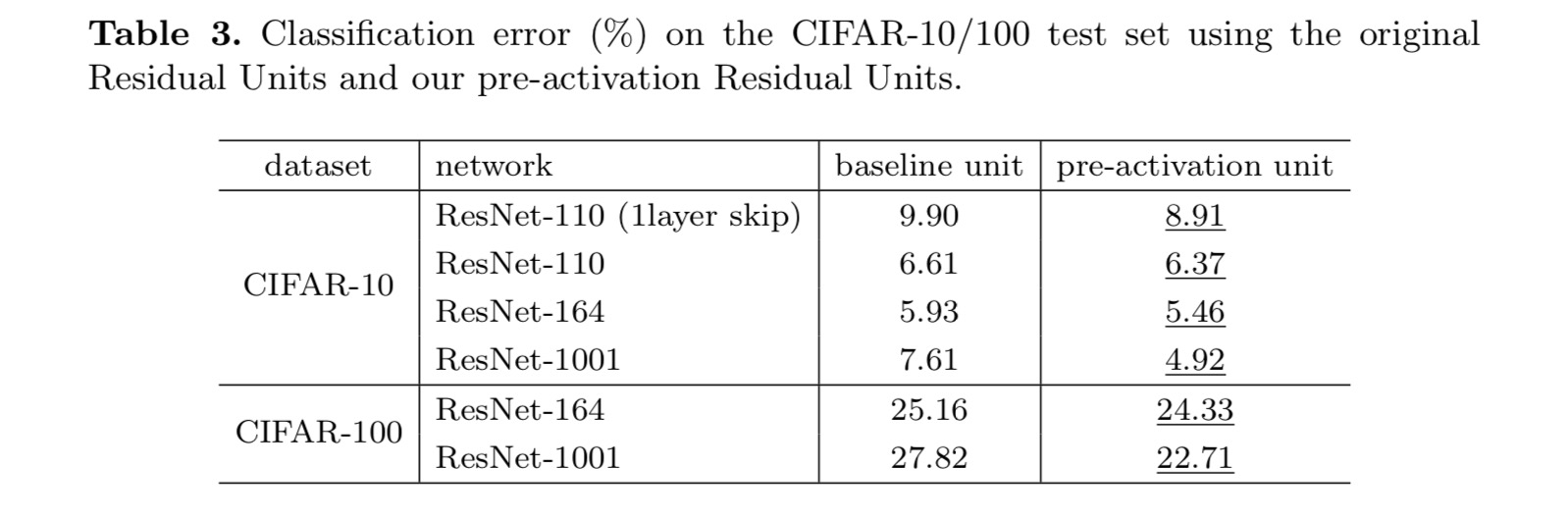
Conclusion

Cet article étudie les formulations de propagation derrière les mécanismes de connexion des réseaux résiduels profonds. Nos dérivations impliquent que les connexions de raccourci d’identité et l’activation de l’identité après addition sont essentielles pour faciliter la propagation de l’information. Les expériences d’ablation démontrent des phénomènes compatibles avec nos dérivations. Nous présentons également des réseaux profonds de 1000 couches qui peuvent être facilement formés et obtenir une précision améliorée.

Transformation résiduelle agrégée pour les réseaux neuronaux profonds

Introduction

La recherche sur la reconnaissance visuelle est en train de passer de « l’ingénierie des fonctionnalités » à « l’ingénierie des réseaux ». L’effort humain a été déplacé vers la conception de meilleures architectures de réseau pour l’apprentissage des représentations.

La conception d’architectures devient de plus en plus difficile avec le nombre croissant d’hyper-paramètres, surtout lorsqu’il y a beaucoup de couches. Les VGG-net présentent une stratégie simple mais efficace de construction de réseaux très profonds: empiler des blocs de construction de la même forme. Cette stratégie est héritée par des ResNets qui empilent des modules de la même topologie. Cette règle simple réduit les choix libres d’hyper paramètres, et la profondeur est exposée comme une dimension essentielle dans les réseaux de neurones. De plus, nous soutenons que la simplicité de cette règle peut réduire le risque de suradaptation des hyperparamètres à un ensemble de données spécifique. La robustesse des réseaux VGG et ResNets a été prouvée par diverses tâches de reconnaissance visuelle et par des tâches non visuelles impliquant la parole et le langage.

Contrairement aux réseaux VGG, la famille de modèles de création a démontré que des topologies soigneusement conçues sont capables d’obtenir une précision convaincante avec une faible complexité théorique. Les modèles de création ont évolué au fil du temps, mais une propriété commune importante est une stratégie de scission-transformation-fusion. Dans un module de création, l’entrée est divisée en quelques encastrements de dimensions inférieures (par circonvolutions 1×1), transformés par un ensemble de filtres spécialisés (3×3, 5×5, etc.), et fusionnés par concaténation. Le comportement de fusion-transformation fractionnée des modules de création devrait approcher la puissance de représentation des couches larges et denses, mais à une complexité de calcul considérablement inférieure.

Malgré une bonne précision, la réalisation des modèles de création s’est accompagnée d’une série de facteurs de complication. Bien que des combinaisons soigneuses de ces composants donnent d’excellentes recettes de réseau neuronal, il n’est généralement pas clair comment adapter les architectures de création à de nouveaux ensembles de données / tâches, en particulier lorsqu’il y a de nombreux facteurs et hyper-paramètres à concevoir.

Dans cet article, nous présentons une architecture simple qui adopte la stratégie de répétition de couches de VGG/ResNets, tout en exploitant la stratégie de split-transform-merge de manière simple et extensible. Un module de notre réseau effectue un ensemble de transformations, chacune sur une intégration de faible dimension, dont les sorties sont agrégées par sommation. Nous poursuivons une réalisation simple de cette idée — les transformations à agréger sont toutes de la même topologie. Cette conception nous permet d’étendre à n’importe quel grand nombre de transformations sans conceptions spécialisées.

Nous démontrons empiriquement que nos transformations agrégées surpassent le module ResNet d’origine, même dans la condition restreinte de maintenir la complexité de calcul et la taille du modèle. Nous soulignons que s’il est relativement facile d’augmenter la précision en augmentant la capacité (en allant plus loin ou plus loin), les méthodes qui augmentent la précision tout en maintenant (ou en réduisant) la complexité sont rares dans la littérature.

Notre méthode indique que la cardinalité (la taille de l’ensemble des transformations) est une dimension concrète et mesurable qui revêt une importance centrale, en plus des dimensions de largeur et de profondeur. Les expériences démontrent que l’augmentation de la cardinalité est un moyen plus efficace d’obtenir de la précision que d’aller plus loin ou plus loin, en particulier lorsque la profondeur et la largeur commencent à donner des rendements décroissants pour les modèles existants.

Nos réseaux de neurones, nommés ResNeXt (suggérant la dimension suivante), surpassent ResNet-101/152, ResNet-200, Inception-v3 et Inception-ResNet-v2 sur l’ensemble de données de classification ImageNet. En particulier, un ResNeXt à 101 couches est capable d’obtenir une meilleure précision que ResNet-200 mais n’a que 50% de complexité. De plus, ResNeXt présente des conceptions considérablement plus simples que tous les modèles Inception.

Méthode

Nous adoptons une conception hautement modularisée suivant VGG/ResNets. Notre réseau est constitué d’une pile de blocs résiduels. Ces blocs ont la même topologie, et sont soumis à deux règles simples inspirées de VGG/ResNets : (1) si l’on produit des cartes spatiales de même taille, les blocs partagent les mêmes hyper-paramètres (largeur et tailles de filtres), et (2) chaque fois que la carte spatiale est sous-échantillonnée d’un facteur 2, la largeur des blocs est multipliée par un facteur 2. La deuxième règle garantit que la complexité de calcul, en termes de FLOPs (opérations à virgule flottante, en # de multiplication-ajout), est à peu près la même pour tous les blocs.

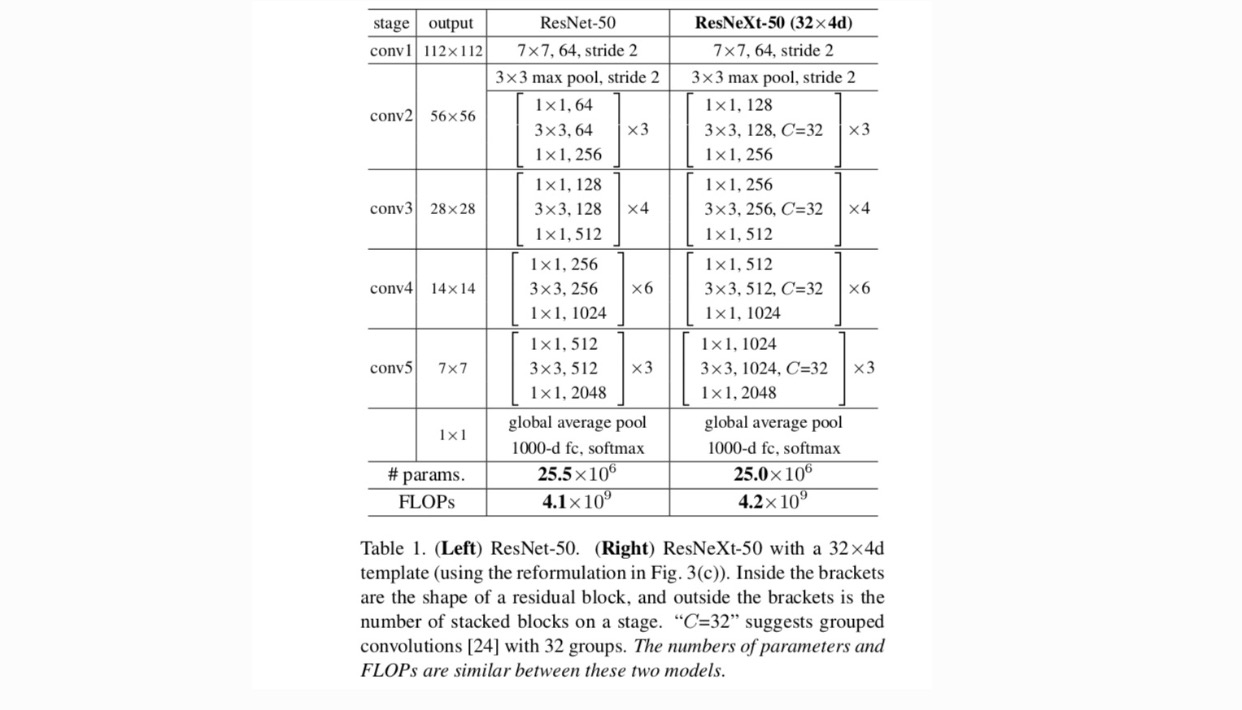
Avec ces deux règles, il suffit de concevoir un module modèle, et tous les modules d’un réseau peuvent être déterminés en conséquence. Ces deux règles réduisent considérablement l’espace de conception et nous permettent de nous concentrer sur quelques facteurs clés. Les réseaux construits selon ces règles sont dans le tableau 1.

Les neurones les plus simples des réseaux de neurones artificiels effectuent un produit interne (somme pondérée), qui est la transformation élémentaire effectuée par des couches entièrement connectées et convolutives.

L’opération ci-dessus peut être refondue comme une combinaison de fractionnement, de transformation et d’agrégation. (1): Fractionnement: le vecteur est découpé en tranches en tant qu’incorporation de faible dimension, et dans ce qui précède, il s’agit d’un sous-espace à une seule dimension (2) Transformation: la représentation de faible dimension est transformée, et dans ce qui précède, elle est simplement mise à l’échelle: (3) Agrégation: les transformations dans toutes les intégrations sont agrégées par.

Compte tenu de l’analyse ci-dessus d’un neurone simple, nous envisageons de remplacer la transformation élémentaire (w_i, x_i) par une fonction plus générique, qui en soi peut également être un réseau. Formellement, nous présentons les transformations agrégées comme :

où peut être une fonction arbitraire. Analogue à un neurone simple, devrait se projeter dans un enrobage (éventuellement de faible dimension), puis le transformer.

On parle de cardinalité. est dans une position similaire à in, mais n’a pas besoin d’être égale et peut être un nombre arbitraire. Nous montrons par des expériences que la cardinalité est une dimension essentielle et peut être plus efficace que les dimensions de largeur et de profondeur.

Dans cet article, nous considérons une façon simple de concevoir les fonctions de transformation : toutes ont la même topologie. Cela étend la stratégie de style VGG consistant à répéter des couches de la même forme. Nous définissons la transformation individuelle comme étant l’architecture en forme de goulot d’étranglement illustrée à la Fig. 1 (à droite). Dans ce cas, la première couche 1×1 dans chacune produit l’enrobage de faible dimension.

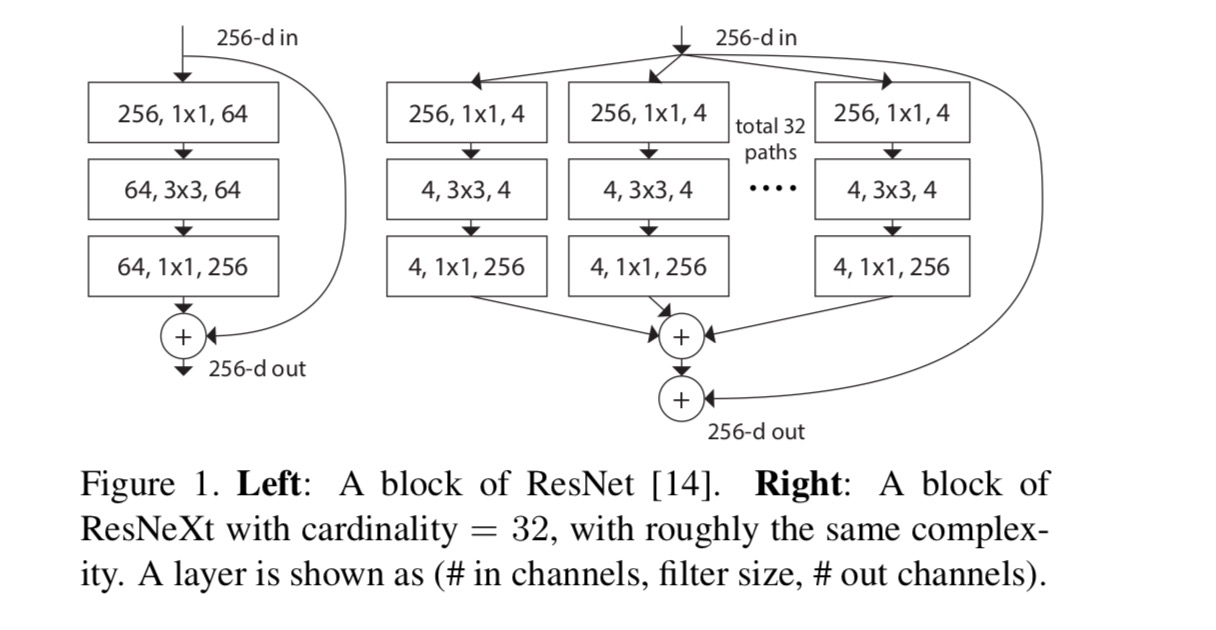
La transformation agrégée dans la dernière équation sert de fonction résiduelle :

où est la sortie.

Les relations entre ResNeXt et Inception-ResNet/Grouped-Convolutions sont illustrées dans la figure suivante:

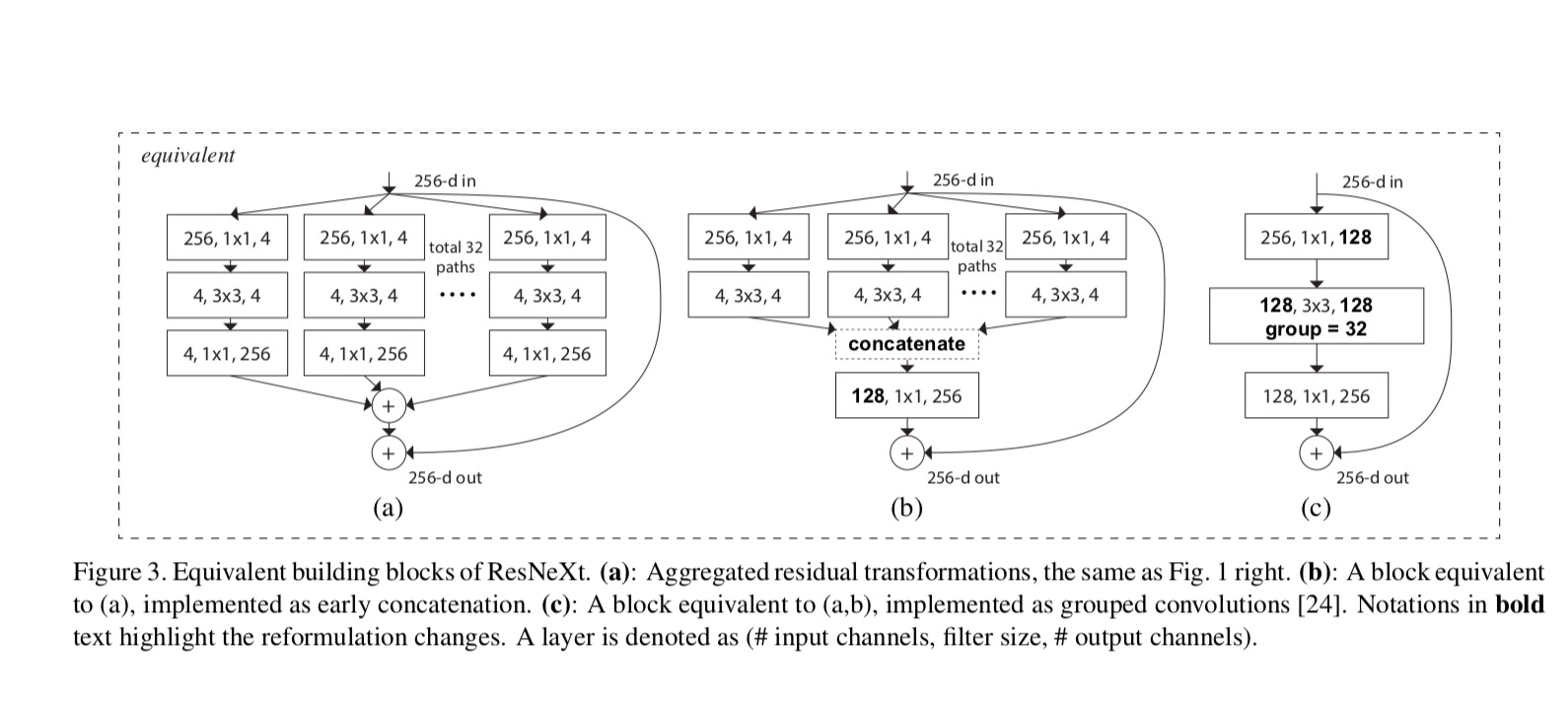
Lorsque nous évaluons différentes cardinalités tout en préservant la complexité, nous voulons minimiser la modification d’autres hyper-paramètres. Nous choisissons d’ajuster la largeur du goulot d’étranglement (par exemple, 4-d sur la figure 1 (à droite)), car il peut être isolé de l’entrée et de la sortie du bloc. Cette stratégie n’introduit aucun changement aux autres hyper-paramètres (profondeur ou largeur d’entrée / sortie des blocs), il est donc utile pour nous de nous concentrer sur l’impact de la cardinalité.

Sur la Fig. 1 (à gauche), le bloc de goulot d’étranglement ResNet d’origine a des paramètres et des FLOPs proportionnels (sur la même taille de carte d’entités). Avec la largeur du goulot d’étranglement, notre gabarit sur la Fig. 1 (à droite) a: paramètres et FLOPs proportionnels. Quand et, ce nombre. Le tableau suivant montre la relation entre la cardinalité et la largeur du goulot d’étranglement.

Expériences

Cardinalité par rapport à la largeur. Nous évaluons d’abord le compromis entre la cardinalité et la largeur du goulot d’étranglement, sous la complexité préservée, comme indiqué dans le tableau 2. Le tableau 3 montre les résultats. En comparaison avec ResNet-50, le ResNeXt-50 32×4d présente une erreur de validation de 22,2%, soit 1,7% de moins que les 23,9% de base de ResNet. Avec la cardinalité qui passe de 1 à 32 tout en conservant la complexité, le taux d’erreur ne cesse de diminuer. De plus, le ResNeXt 32×4d a également une erreur d’entraînement beaucoup plus faible que le countetpart ResNet, suggérant que les gains ne proviennent pas de la régularisation mais de représentations plus fortes.

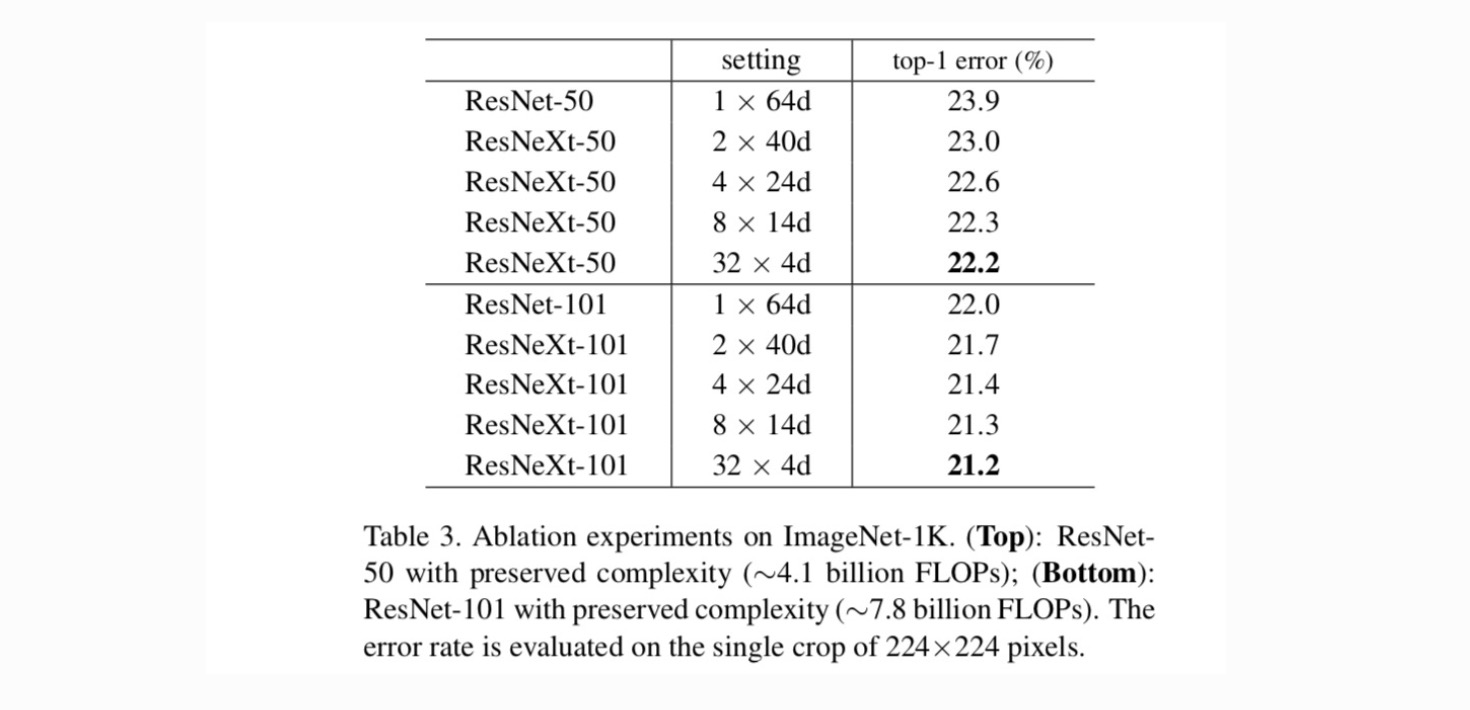
Augmentation de la cardinalité par rapport à Plus profond / plus large.

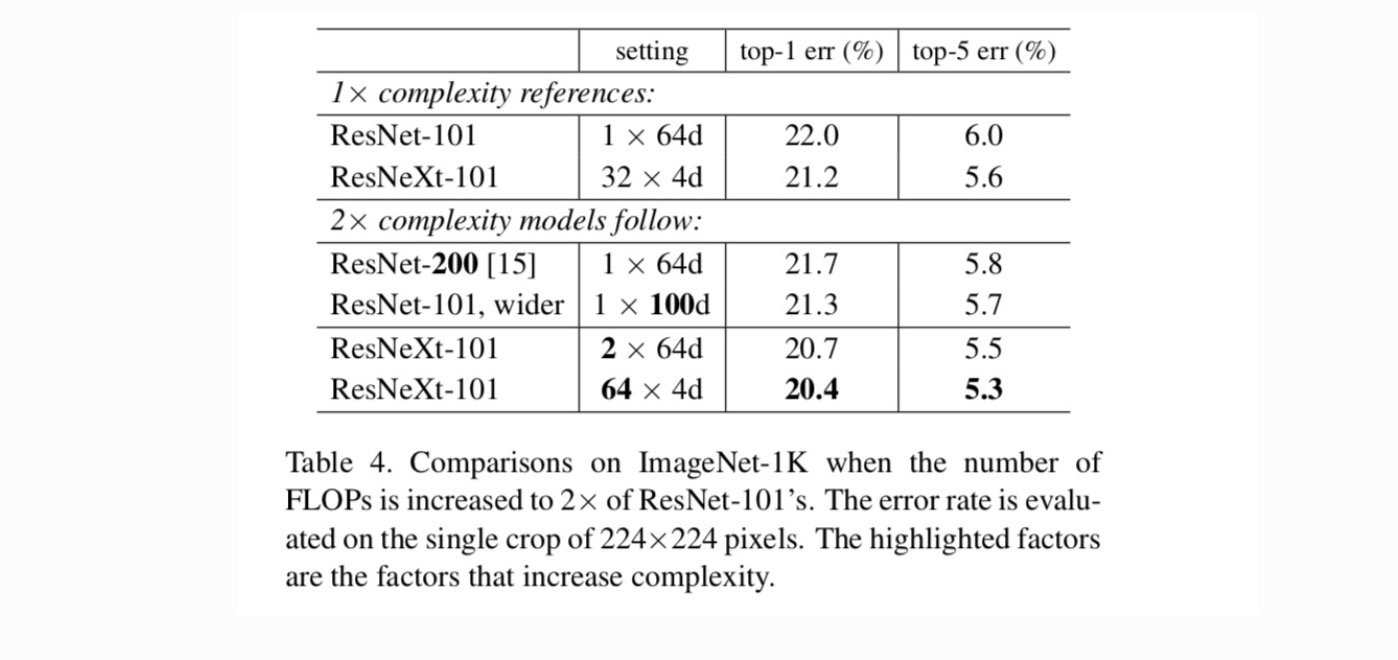
Ensuite, nous étudions la complexité croissante en augmentant la cardinalité C ou en augmentant la profondeur ou la largeur. Nous comparons les variantes suivantes (1) En allant plus loin à 200 couches. Nous adoptons le ResNet-200. (2) Aller plus large en augmentant la largeur du goulot d’étranglement. (3) Augmentation de la cardinalité en doublant C.

Le tableau 4 montre qu’une augmentation de la complexité de 2× réduit systématiquement les erreurs par rapport à la ligne de base ResNet-101 (22,0%). Mais l’amélioration est faible en allant plus loin (ResNet-200, de 0,3%) ou plus large (ResNet-101 plus large, de 0,7%). Au contraire, l’augmentation de la cardinalité C donne de bien meilleurs résultats que d’aller plus loin ou plus loin.

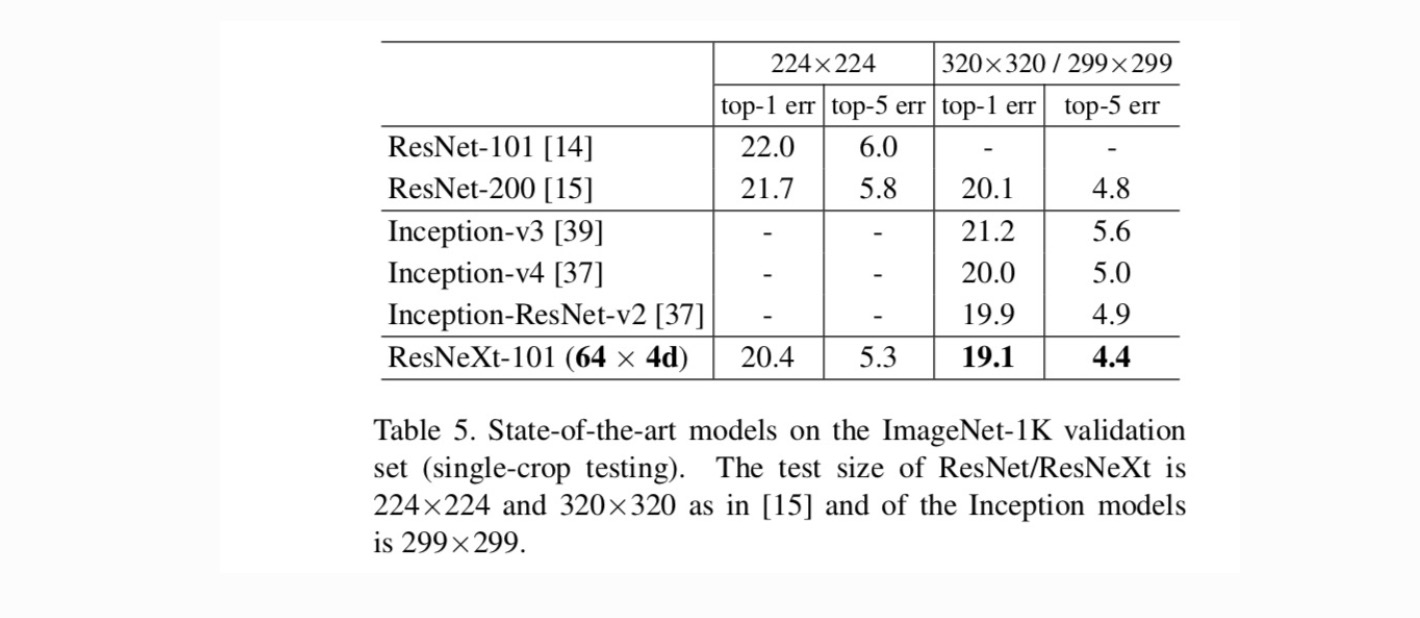
Comparaisons avec des résultats de pointe. Le tableau 5 montre plus de résultats de tests de culture unique sur l’ensemble de validation ImageNet. Nos résultats se comparent favorablement avec ResNet, Inception-v3/v4 et Inception-ResNet-v2, atteignant un taux d’erreur top-5 unique de 4,4%. De plus, notre conception d’architecture est beaucoup plus simple que tous les modèles Inception et nécessite beaucoup moins d’hyper-paramètres à définir manuellement.