
L’apprentissage automatique est finalement utilisé pour prédire les résultats compte tenu d’un ensemble de fonctionnalités. Par conséquent, tout ce que nous pouvons faire pour généraliser les performances de notre modèle est considéré comme un gain net. Le décrochage est une technique utilisée pour empêcher un modèle de surajuster. L’abandon fonctionne en réglant aléatoirement les bords sortants des unités cachées (neurones qui composent les couches cachées) à 0 à chaque mise à jour de la phase d’entraînement. Si vous jetez un coup d’œil à la documentation Keras pour la couche d’abandon scolaire, vous verrez un lien vers un livre blanc écrit par Geoffrey Hinton et ses amis, qui explique la théorie de l’abandon scolaire.
Dans l’exemple suivant, nous utiliserons Keras pour construire un réseau de neurones dans le but de reconnaître les chiffres écrits à la main.
from keras.datasets import mnist
from matplotlib import pyplot as plt
plt.style.use('dark_background')
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation, Dropout
from keras.utils import normalize, to_categorical
Nous utilisons Keras pour importer les données dans notre programme. Les données sont déjà divisées en ensembles de formation et de test.
(X_train, y_train), (X_test, y_test) = mnist.load_data()
Jetons un coup d’œil pour voir avec quoi nous travaillons.
plt.imshow(x_train, cmap = plt.cm.binary)
plt.show()

Une fois que nous avons terminé la formation sur le modèle, il devrait être capable de reconnaître l’image précédente comme un cinq.
Il y a un peu de prétraitement que nous devons effectuer au préalable. Nous normalisons les pixels (entités) de sorte qu’ils vont de 0 à 1. Cela permettra au modèle de converger vers une solution beaucoup plus rapidement. Ensuite, nous transformons chacune des étiquettes cibles pour un échantillon donné en un tableau de 1 et 0 où l’index du nombre 1 indique le chiffre que représente l’image. Nous le faisons parce que sinon notre modèle interpréterait le chiffre 9 comme ayant une priorité plus élevée que le nombre 3.
X_train = normalize(X_train, axis=1)
X_test = normalize(X_test, axis=1)
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
Sans décrochage
Avant d’introduire une matrice à 2 dimensions dans un réseau de neurones, nous utilisons une couche d’aplatissement qui la transforme en un tableau à 1 dimension en ajoutant chaque ligne suivante à celle qui l’a précédée. Nous allons utiliser deux couches cachées composées de 128 neurones chacune et une couche de sortie composée de 10 neurones, chacune pour l’un des 10 chiffres possibles. La fonction d’activation softmax renvoie la probabilité qu’un échantillon représente un chiffre donné.

Puisque nous essayons de prédire les classes, nous utilisons la crossentropie catégorielle comme fonction de perte. Nous mesurerons les performances du modèle avec précision.
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
Nous mettons 10% des données de côté pour la validation. Nous l’utiliserons pour comparer la tendance d’un modèle à surajuster avec et sans décrochage. Une taille de lot de 32 implique que nous allons calculer le gradient et faire un pas dans la direction du gradient avec une magnitude égale au taux d’apprentissage, après avoir passé 32 échantillons à travers le réseau de neurones. Nous faisons cela un total de 10 fois comme spécifié par le nombre d’époques.
history = model.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

Nous pouvons tracer les précisions d’entraînement et de validation à chaque époque en utilisant la variable d’historique renvoyée par la fonction fit.
Comme vous pouvez le voir, sans abandon, la perte de validation cesse de diminuer après la troisième époque.

As you can see, without dropout, the validation accuracy tends to plateau around the third epoch.

Using this simple model, we still managed to obtain an accuracy of over 97%.
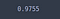
test_loss, test_acc = model.evaluate(X_test, y_test)
test_acc
Abandon
Il y a un débat quant à savoir si l’abandon doit être placé avant ou après la fonction d’activation. En règle générale, placez le décrochage après la fonction d’activation pour toutes les fonctions d’activation autres que relu. En passant 0,5, chaque unité cachée (neurone) est définie sur 0 avec une probabilité de 0,5. En d’autres termes, il y a un changement de 50% que la sortie d’un neurone donné sera forcée à 0.

Encore une fois, puisque nous essayons de prédire les classes, nous utilisons la crossentropie catégorielle comme fonction de perte.
model_dropout.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
En fournissant le paramètre de fractionnement des validations, le modèle distinguera une fraction des données d’apprentissage et évaluera la perte et toutes les métriques du modèle sur ces données à la fin de chaque époque. Si la prémisse derrière l’abandon tient, alors nous devrions voir une différence notable dans la précision de validation par rapport au modèle précédent. Le paramètre shuffle mélangera les données d’entraînement avant chaque époque.
history_dropout = model_dropout.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

Comme vous pouvez le voir, la perte de validation est nettement inférieure à celle obtenue en utilisant le modèle normal.

Comme vous pouvez le voir, le modèle a convergé beaucoup plus rapidement et a obtenu une précision proche de 98% sur l’ensemble de validation, alors que le modèle précédent a atteint un plateau autour de la troisième époque.

La précision obtenue sur l’ensemble de tests n’est pas très différente de celle obtenue à partir du modèle sans abandon. Cela est probablement dû au nombre limité d’échantillons.
test_loss, test_acc = model_dropout.evaluate(X_test, y_test)
test_acc

Pensées finales
L’abandon peut aider un modèle à se généraliser en réglant aléatoirement la sortie d’un neurone donné à 0. En réglant la sortie à 0, la fonction de coût devient plus sensible aux neurones voisins modifiant la façon dont les poids seront mis à jour pendant le processus de rétropropagation.