Franck-Condon-princippet beskriver intensiteterne af vibroniske overgange eller absorption eller emission af en foton. Det hedder, at når et molekyle gennemgår en elektronisk overgang, såsom ionisering, oplever molekylets nukleare konfiguration ingen signifikant ændring. Dette skyldes faktisk, at kerner er meget mere massive end elektroner, og den elektroniske overgang finder sted hurtigere, end kernerne kan reagere. Når kernen tilpasser sig den nye elektroniske konfiguration, siger teorien, at den skal gennemgå en vibration.
Hvis vi forestiller os den lodrette overgang fra jord til ophidset elektronisk tilstand som forekommende fra en vibrationsbølgefunktion,der giver en sandsynlighedsfordeling for at finde kernerne i et give-område af rummet, kan vi bestemme sandsynligheden for et givet vibrationsniveau fra overlapningsintegralet \(S_{v’, v}\), som giver overlapningen af vibrationsbølgefunktionen i jorden og ophidset tilstand. Det\ (v’\) kvantetal henviser til jordtilstand og\ (v\) kvantetal henviser til ophidset tilstand. Overgangssandsynligheden kan adskilles i elektroniske og nukleare dele ved hjælp af Condon-tilnærmelsen.
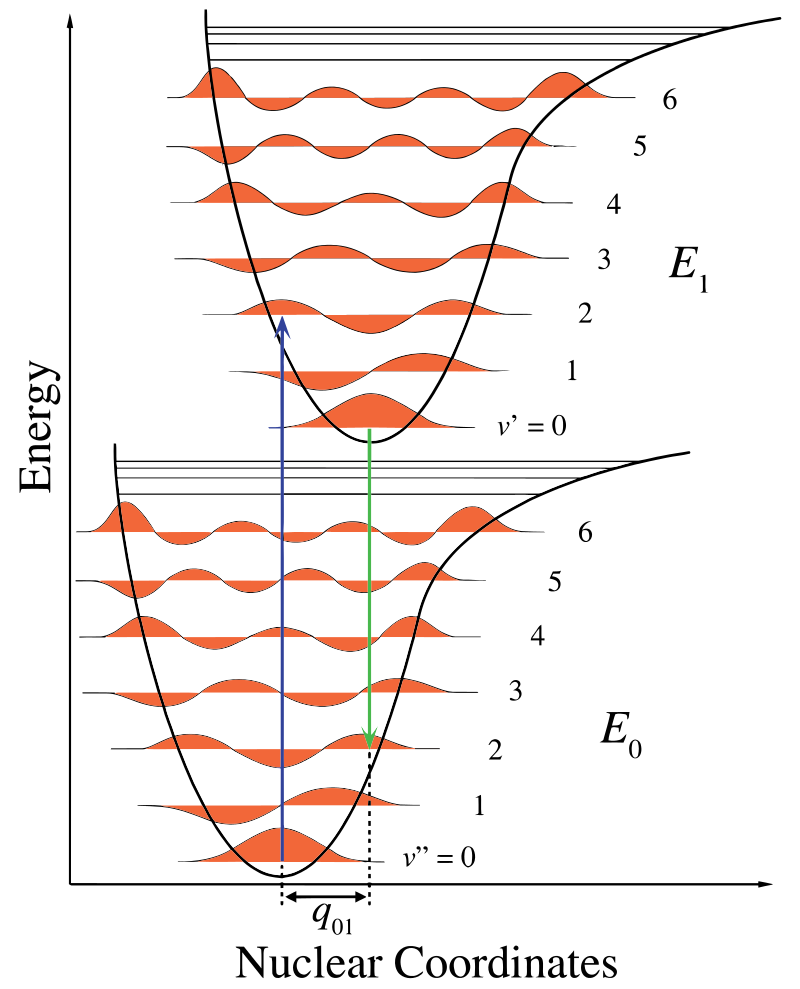
i figur \(\Sideindeks{1}\) viser atomaksen en konsekvens af den internukleære adskillelse, og den vibroniske overgang er angivet med de blå og grønne lodrette pile. Denne figur viser tre ting:
- en absorption fører til en højere energitilstand,
- fluorescens fører til en lavere energitilstand, og
- skiftet i nukleare koordinater mellem jorden og ophidset tilstand er tegn på en ny ligevægtsposition for nukleart interaktionspotentiale. Det faktum, at fluorescenspilen er kortere end absorptionen, indikerer, at den har mindre energi, eller at dens bølgelængde er længere.
den klassiske Condon-tilnærmelse
Condon-tilnærmelse er antagelsen om, at den elektroniske overgang sker på en kort tidsskala sammenlignet med nuklear bevægelse, så overgangssandsynligheden kan beregnes ved en fast nuklear position.
denne ændring i vibrationer opretholdes under en tilstand kaldet hurtig elektronisk ophidselse. De resulterende Coulombiske kræfter producerer en ligevægt som vist i figuren for kernerne betegnet et vendepunkt. Vendepunktet kan kortlægges ved at tegne en lodret linje fra minimum af den nedre kurve til skæringspunktet mellem den højere elektroniske tilstand. Denne procedure kaldes en lodret overgang og blev diskuteret før i sammenhæng med fotoelektronspektroskopi (en anden elektronisk spektroscoy)..Franck-Condon-princippet forklarer de relative intensiteter af vibroniske overgange ved at relatere sandsynligheden for en vibrationsovergang til overlapningen af vibrationsbølgefunktionerne. Det hedder, at sandsynligheden for, at en vibrationsovergang forekommer, vægtes af Franck-Condon-overlapningsintegralet:
\
inden for Franck-Condon-tilnærmelsen betragtes kernerne som “faste” under elektroniske overgange. Således kan elektroniske overgange betragtes som lodrette overgange på elektroniske potentielle energikurver (vieriske overgange i figur \(\Sideindeks{1}\)).
kvante Franck-Condon-princippet
Franck-Condon-princippet har både en klassisk og Kvanteanvendelse. Klassisk er Franck-Condon-princippet den tilnærmelse, at en elektronisk overgang mest sandsynligt vil forekomme uden ændringer i kernernes positioner i den molekylære enhed og dens miljø. Den resulterende tilstand kaldes en Franck-Condon-tilstand, og den involverede overgang, en lodret overgang. Den kvantemekaniske formulering af dette princip er, at intensiteten af en vibronisk overgang er proportional med kvadratet af overlapningsintegralet mellem de vibrationsbølgefunktioner i de to tilstande, der er involveret i overgangen.Franck-Condon-princippet er baseret på Born-Oppenheimer-tilnærmelsen, som tillader adskillelse af de elektroniske \(k\) og nukleare \(K\) bølgefunktioner i betragtning af den samlede bølgefunktion.
\
da overgangsoperatøren, \(\hat{\mu}(k)\), kun er afhængig af den elektroniske komponent, kan de nukleare komponenter adskilles fra overgangsmomentintegralet, der dikterer sandsynligheden for, at overgangen finder sted:
&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\tekst{nuclear overlap}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align}\]
Hvis den nukleare overlapningsintegral er nul for denne overgang, vil overgangen ikke blive observeret, uanset størrelsen af den elektroniske faktor.
\(S_{00}\) overgang evalueret inden for harmonisk Oscillatormodel
den nukleare overlapning for nul-nul-overgangen \(S_{00}\) kan beregnes ganske enkelt ved hjælp af definitionen af den gaussiske form for de harmoniske oscillatorbølgefunktioner.
nulpunktsbølgefunktionen i jordelektronisk tilstand er
\
nulpunktsbølgefunktionen i den ophidsede elektroniske tilstand er
\
hvor
- \(\alpha = \dfrac {\
- \(r_e\) er ligevægtsbindingslængden i jordelektronisk tilstand
- \(k_e\) er Ligevægtsbindingslængden i ophidset elektronisk tilstand
den nukleare overlapningsintegral er
\
eksponenten i ligning\ (\ref{FC1}\) kan udvides som
\
og vi bruger
\
og
\
for at erstatte og fuldføre firkanten inde i integralet. Vi kan udtrykke
\.\]
således er integralet i ligning \(\ref{FC2}\)
\
integralet er en Gaussisk integral. Du kan vise, at hvis vi lader \(S = \S{\alpha}\{R-1/2(R_e + S_e)\}\) så \(S = \S{\alpha} dR\) og integralet bliver
\
denne integral er allerede løst, fra en tabel med integraler bliver ligning \(\ref{FC3}\)
\
Vi ville følge den samme procedure for at beregne overlapningen af nulniveauvibrationen i jorden til det første ophidsede vibrationsniveau i den ophidsede tilstand: \(S_{01}\).
\(S_{01}\) overgang evalueret inden for harmonisk Oscillatormodel
for at beregne overlapningen af nul jordtilstandsniveau (\(v=0\)) med det første ophidsede tilstandsniveau (\(v’=1\)) bruger vi Hermite polynomium \(H_1(h) =2H) til at beskrive den ophidsede tilstandsbølgefunktion (se her for en gennemgang af harmoniske oscillatorbølgefunktioner). Here \(s = \ sv{\alpha} (R – SV)\).
\
med nulpunktsbølgefunktionen i jorden elektronisk tilstand er
\
den første ophidsede tilstandsbølgefunktion i den ophidsede elektroniske tilstand er
\
overlapningen af nul jordtilstandsniveau med det første ophidsede tilstandsniveau (ligning \(\ref{fc01}\)) er derefter
\
og
\
de samme substitutioner kan foretages som ovenfor, så integralet kan skrives som (ikke vist og skal demonstreres i en hjemmearbejde øvelser) og det endelige resultat er
\
Vi kunne fortsætte og beregne den overlapning af nulniveauet i jordtilstanden med alle de højere lysvibrationsniveauer: \(S_{02}\), \(S_{03}\) osv. Hvert udtryk svarer til en overgang med en anden energi, da vibrationsniveauerne har forskellige energier. Absorptionsbåndet ser derefter ud som en progression (en Franck-Condon-progression) af overgange mellem forskellige niveauer hver med sin egen sandsynlighed.
Franck-Condon progressioner
for at forstå betydningen af ovenstående formel for FC-faktoren, lad os undersøge en jord og ophidset tilstand potentiel energioverflade ved \(T = 0\) Kelvin. Nedenfor er to tilstande adskilt af 8.000 cm-1 i energi. Dette er energiseparation mellem bunden af deres potentielle Brønde, men også mellem de respektive nulpunkts energiniveauer. Lad os antage, at bølgenantallet af vibrationstilstanden er 1.000 cm-1, og at bindingslængden øges på grund af det faktum, at en elektron fjernes fra en bindingsbane og placeres i en anti-bindingsbane ved elektronisk ophidselse.
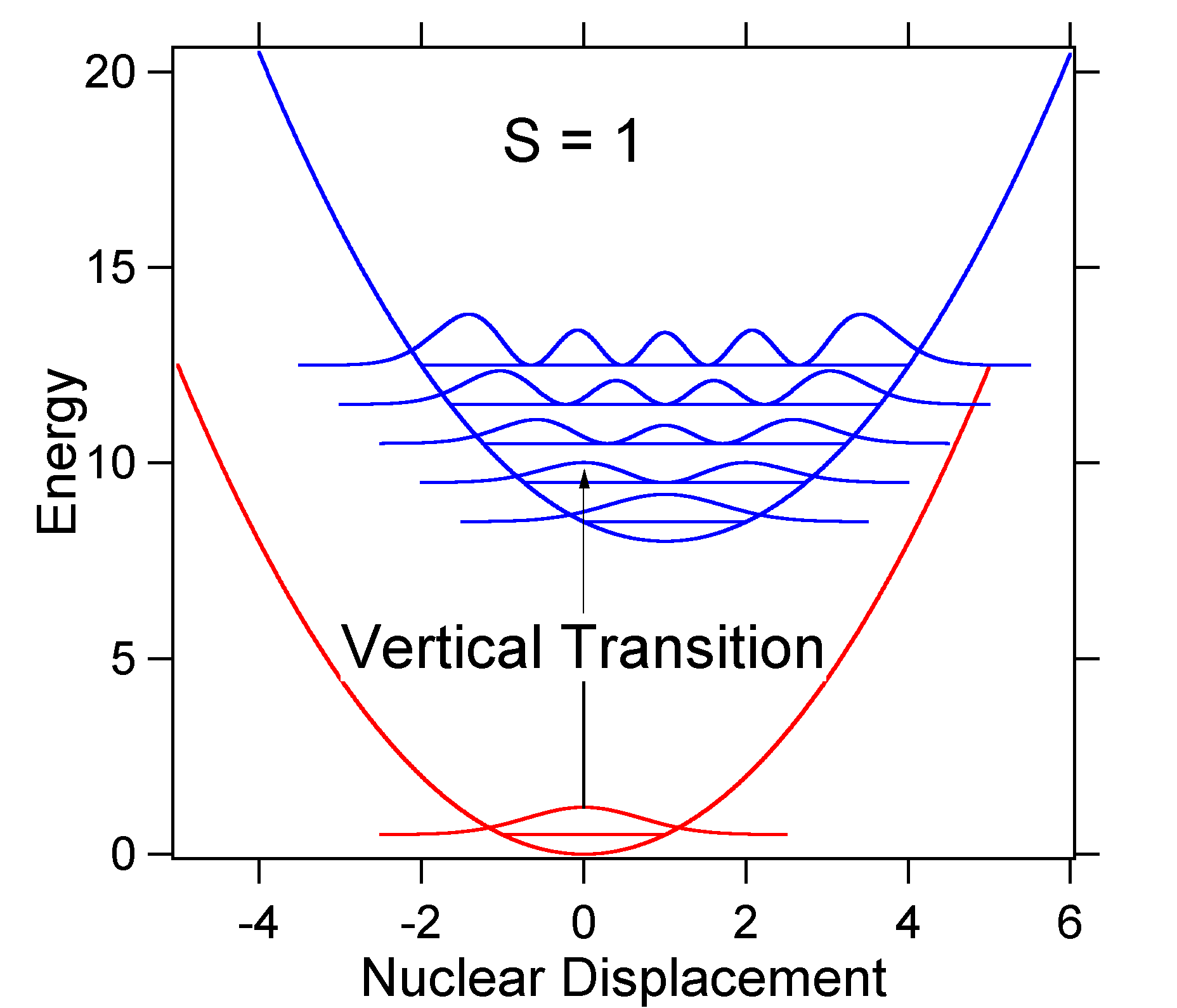
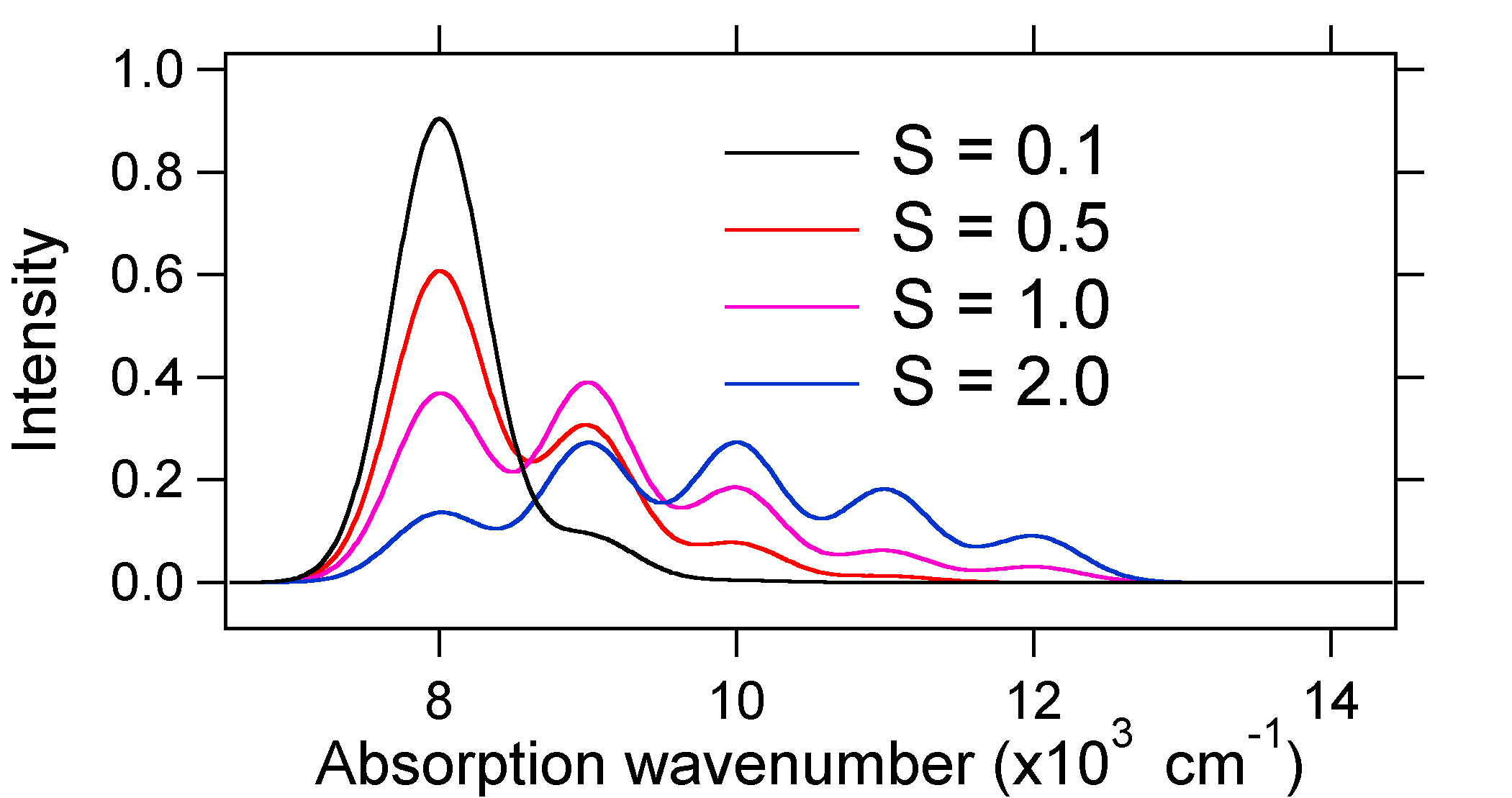
ifølge ovenstående model for Franck-Condon-faktoren ville vi generere et” stick ” – spektrum (figur \(\Sideindeks{3}\)), hvor hver vibrationsovergang er uendelig smal, og overgangen kun kan forekomme, når \(E = h\nu\) nøjagtigt. For eksempel blev de potentielle energioverflader givet til S = 1, og overgangssandsynligheden på hvert niveau er givet af pindene (sort) i nedenstående figur.
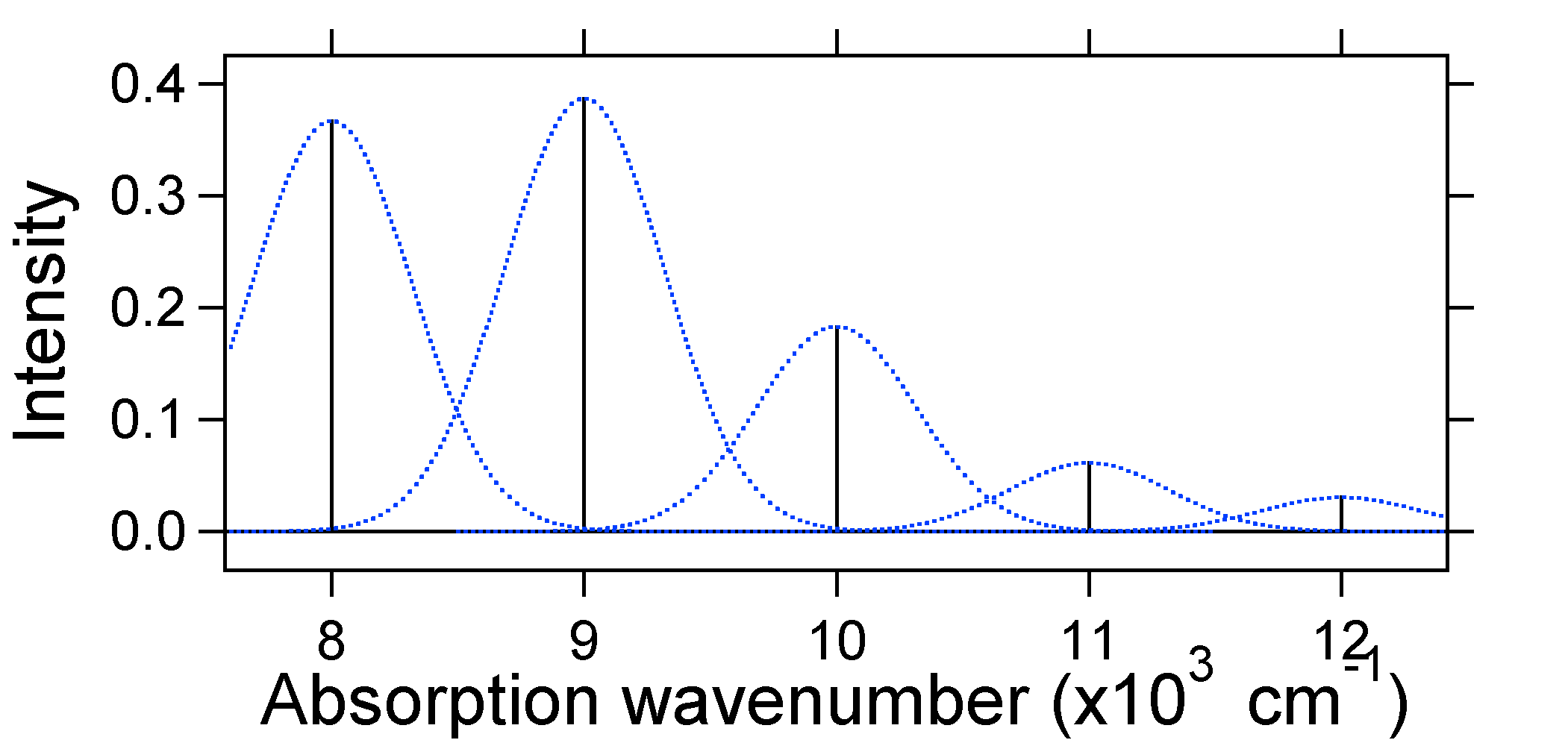
de stiplede Gaussere, der omgiver hver pind, giver et mere realistisk billede af, hvordan absorptionsspektret skal se ud. På dette første sted vil hvert energiniveau (pind) blive givet en vis bredde ved, at staten har en endelig levetid. En sådan udvidelse kaldes homogen udvidelse, da den påvirker alle molekylerne i ensemblet på en lignende måde. Der er også udvidelse på grund af små forskelle i miljøet i hvert molekyle. Denne type udvidelse kaldes inhomogen udvidelse. Uanset oprindelse blev modellen ovenfor oprettet ved hjælp af en Gaussisk udvidelse
den nukleare forskydning mellem jorden og ophidset tilstand bestemmer formen på absorptionsspektret. Lad os undersøge både en mindre og en stor ophidset tilstand forskydning. If \(s = prit\) og de potentielle energiflader i dette tilfælde er:
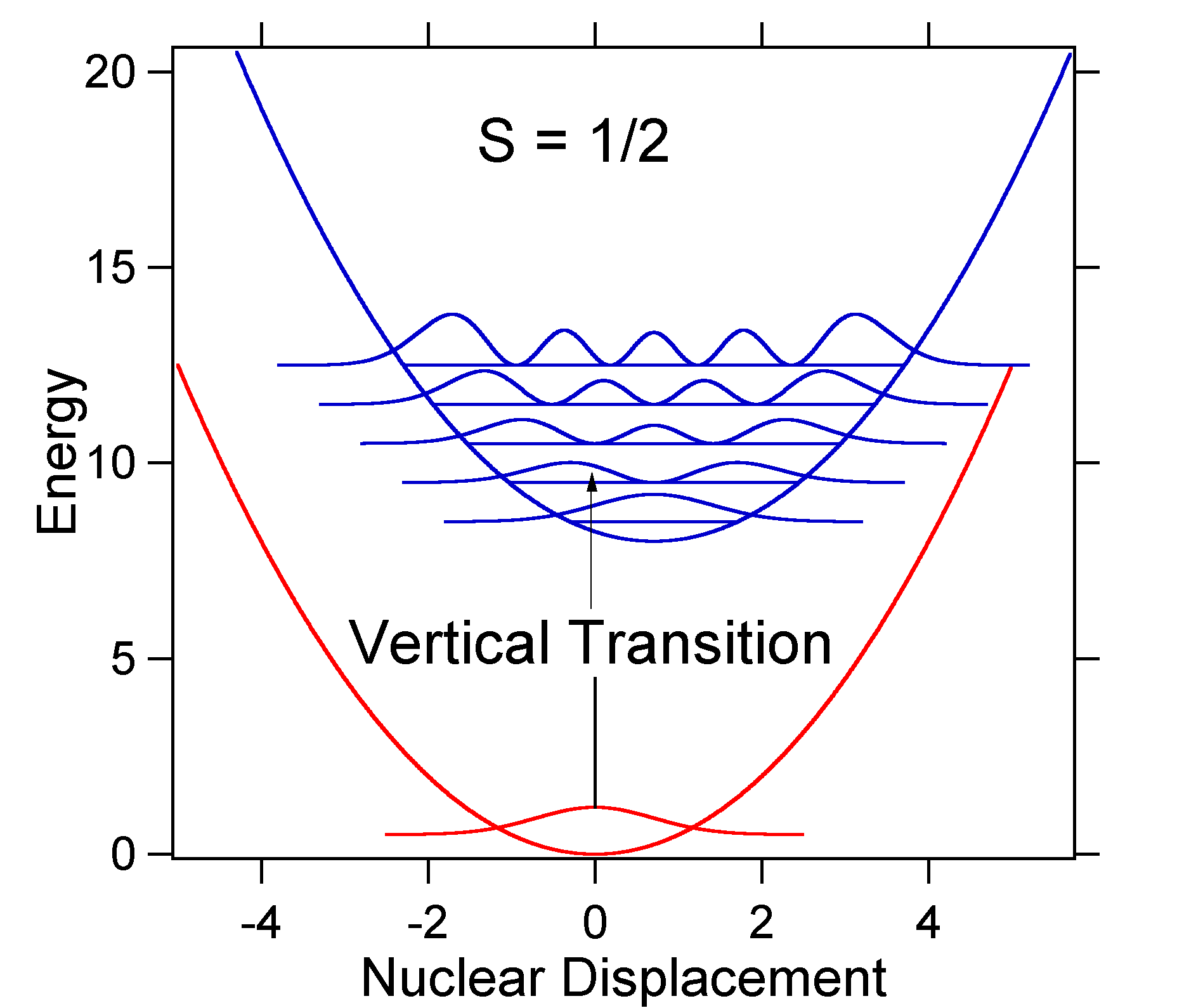
For this case the “stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
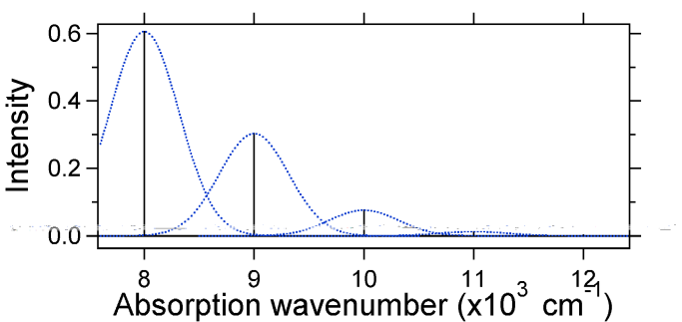
Bemærk, at nul-nul eller \(s_{0,0}\) vibrationsovergang er meget stor i tilfælde, hvor forskydningen er lille.
som en generel tommelfingerregel giver \(S\) konstanten forholdet mellem intensiteten af \(v = 2\) overgangen til \(v = 1\) overgangen. I dette tilfælde siden \(S = 0,5\) er \(v=2\) overgangen 0,5 intensiteten af \(v=1\) overgang.
som et eksempel på en større forskydning er dispositionen af de potentielle energiflader for S = 2 vist nedenfor.
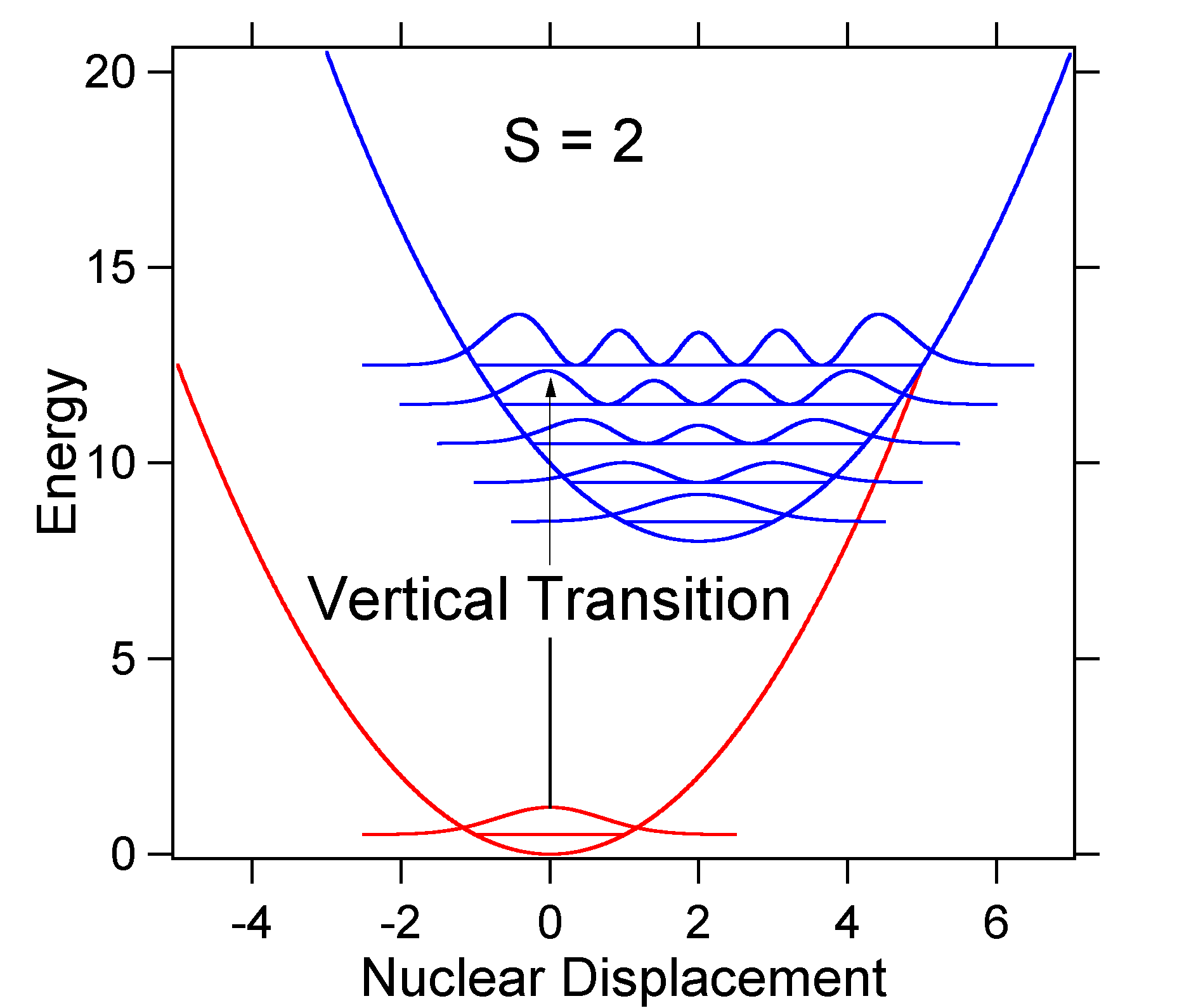
den større forskydning resulterer i nedsat overlapning af jordtilstandsniveauet med V = 0-niveauet for den ophidsede tilstand. Den maksimale intensitet opnås i højere vibrationsniveauer som vist i pindspektret.
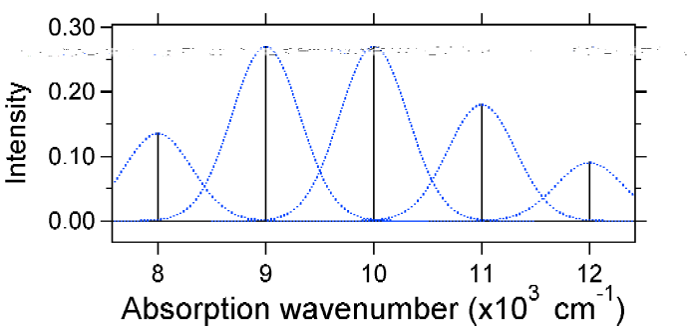
de absorptionsspektre, der er afbildet nedenfor, har alle den samme integrerede intensitet, men deres former ændres på grund af det forskellige omfang af forskydning af den ophidsede tilstandspotentielle energioverflade.
så arten af de relative vibroniske båndintensiteter kan fortælle os, om der er en forskydning af ligevægten nuklear koordinat, der ledsagede en overgang. Hvornår vil der være en stigning i bindingslængden (dvs. \(K_e > R_e\))? Dette sker, når en elektron fremmes fra en bindingsmolekylær orbital til en ikke-bindende eller anti-bindende molekylære orbitaler (dvs.når bindingsrækkefølgen er mindre i ophidset tilstand end jordtilstanden).
- ikke-bonding molecular orbital \(\højre pil\) bonding molecular orbital
- binding molecular orbital
- Anti-bonding molecular orbital \(\højre pil\) ikke-bonding molecular orbital
kort sagt, når bindingsrækkefølgen er lavere i ophidset tilstand end i jordtilstand, så \(K_e > r_e\); en stigning i obligationslængde vil forekomme, når dette sker.
- J. M. Luis, D. M. biskop, B. Kirtman. En anden tilgang til beregning af Franck–Condon faktorer, herunder anharmonicitet. J. Chem. Phys., 120 (2004), s.813-822.
- Atkins, Peter og Julio De Paula. Fysisk kemi til biovidenskab. 2006. Fri mand og kompagni. s.563-564
- Franck-Condon princip. 1996, 68, 2243. IUPAC kompendium af kemisk terminologi 2. udgave (1997). www.iupac.org/goldbook/F02510.pdf
- E. Rabinvitch og Govindjee. Lysabsorption og skæbne af spænding af energi. 1969. Franck-Condon Princip. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
Contributors
- Matthe si lynlås
-
Stefan Fransen (North Carolina State University)