
et kunstigt neuralt netværk (ann) er lavet af mange sammenkoblede neuroner:
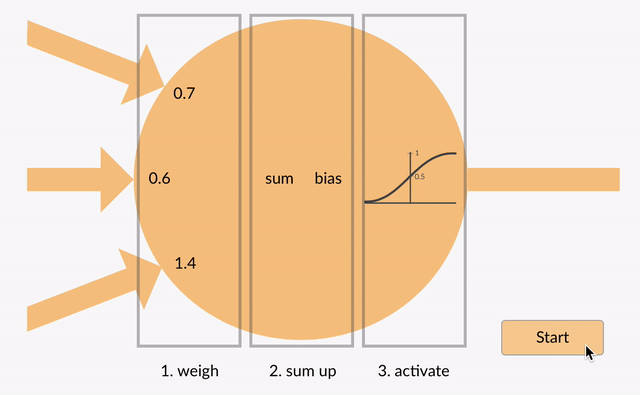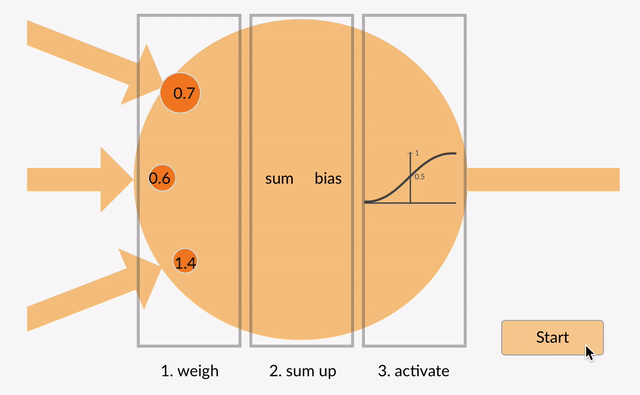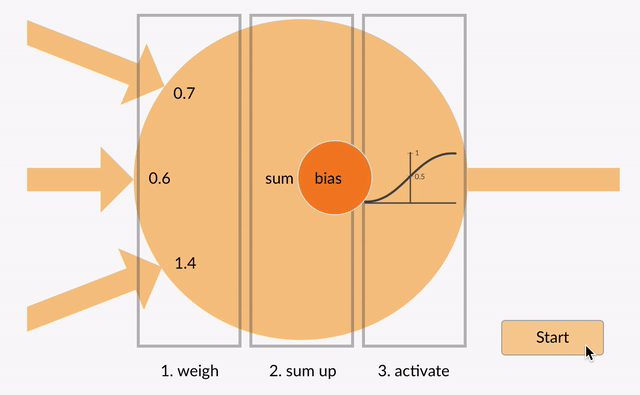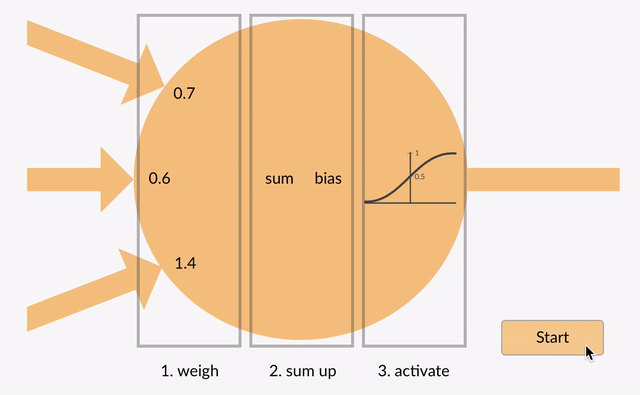
hver neuron tager nogle flydende punktnumre (f.eks. 1,0, 0,5, -1.0) og multiplicerer dem med nogle andre flydende punktnumre (f. eks. 0,7, 0,6, 1,4) kendt som vægte (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Vægtene fungerer som en mekanisme til at fokusere på eller ignorere visse input.

de vægtede indgange bliver derefter opsummeret (f. eks. 0.7 + 0.3 + -1.4 = -0.4) sammen med en bias værdi (f.eks. -0.4 + -0.1 = -0.5).den summerede værdi omdannes nu til en outputværdi (y) i henhold til neuronens aktiveringsfunktion (y = f)). Nogle populære aktiveringsfunktioner er vist nedenfor:

f.eks. -0.5 liter -0.05 hvis vi bruger den utætte korrigerede lineære enhed (utæt relu) aktiveringsfunktion: y = F(H) = F(-0.5) = maks(0.1*-0.5, -0.5) = maks(-0.05, -0.5) = -0.05
neuronens outputværdi (f.eks. -0,05) er ofte et input til en anden neuron.
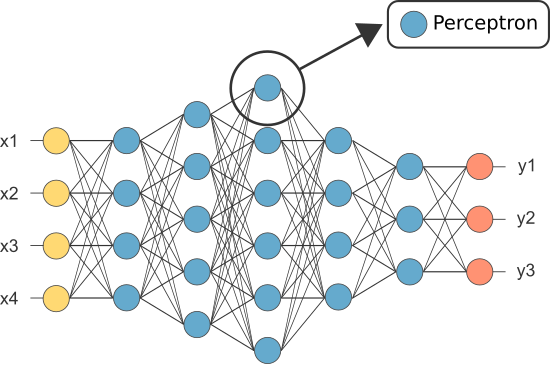
imidlertid var en af de første ann ‘ er kendt som perceptronen, og den bestod af af kun en enkelt neuron.

udgangen af perceptrons (kun) neuron fungerer som den endelige forudsigelse.

lader kode vores egen perceptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Bemærk: Vi har ikke inkluderet nogen læringsalgoritme i vores eksempel ovenfor — vi skal dække læringsalgoritmer i en anden tutorial)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

så hvorfor har vi brug for så mange neuroner i en ANN, hvis nogen vil være tilstrækkelig (som klassifikator)?

desværre er individuelle neuroner kun i stand til at klassificere lineært adskillelige data.

men ved at kombinere neuroner sammen kombinerer vi i det væsentlige deres beslutningsgrænser. Derfor er en ANN sammensat af mange neuroner i stand til at lære komplekse, ikke-lineære beslutningsgrænser.

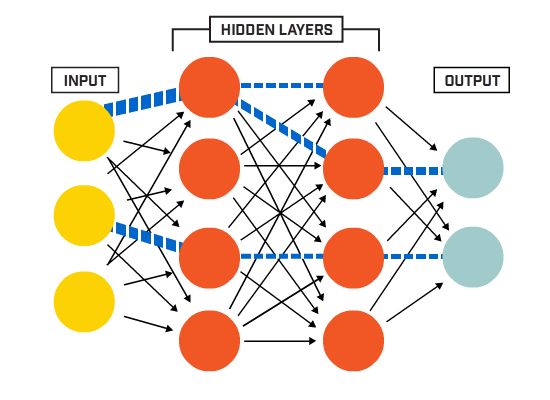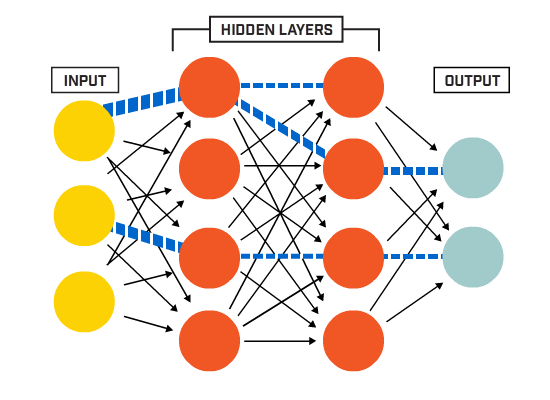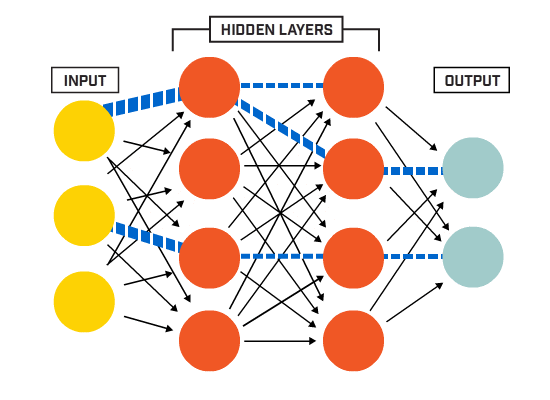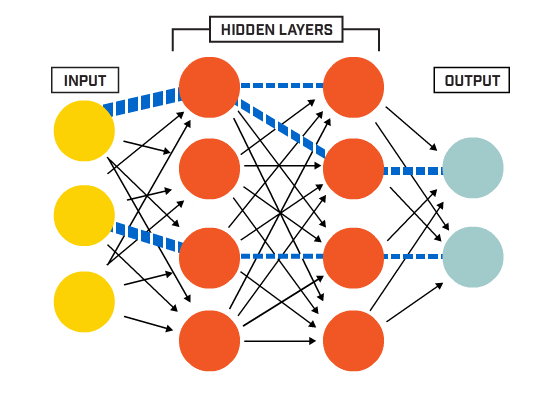
neuroner er forbundet sammen i henhold til en bestemt netværksarkitektur. Selvom der er forskellige arkitekturer, indeholder næsten alle lag. (NB: Neuroner i det samme lag forbinder ikke med hinanden)
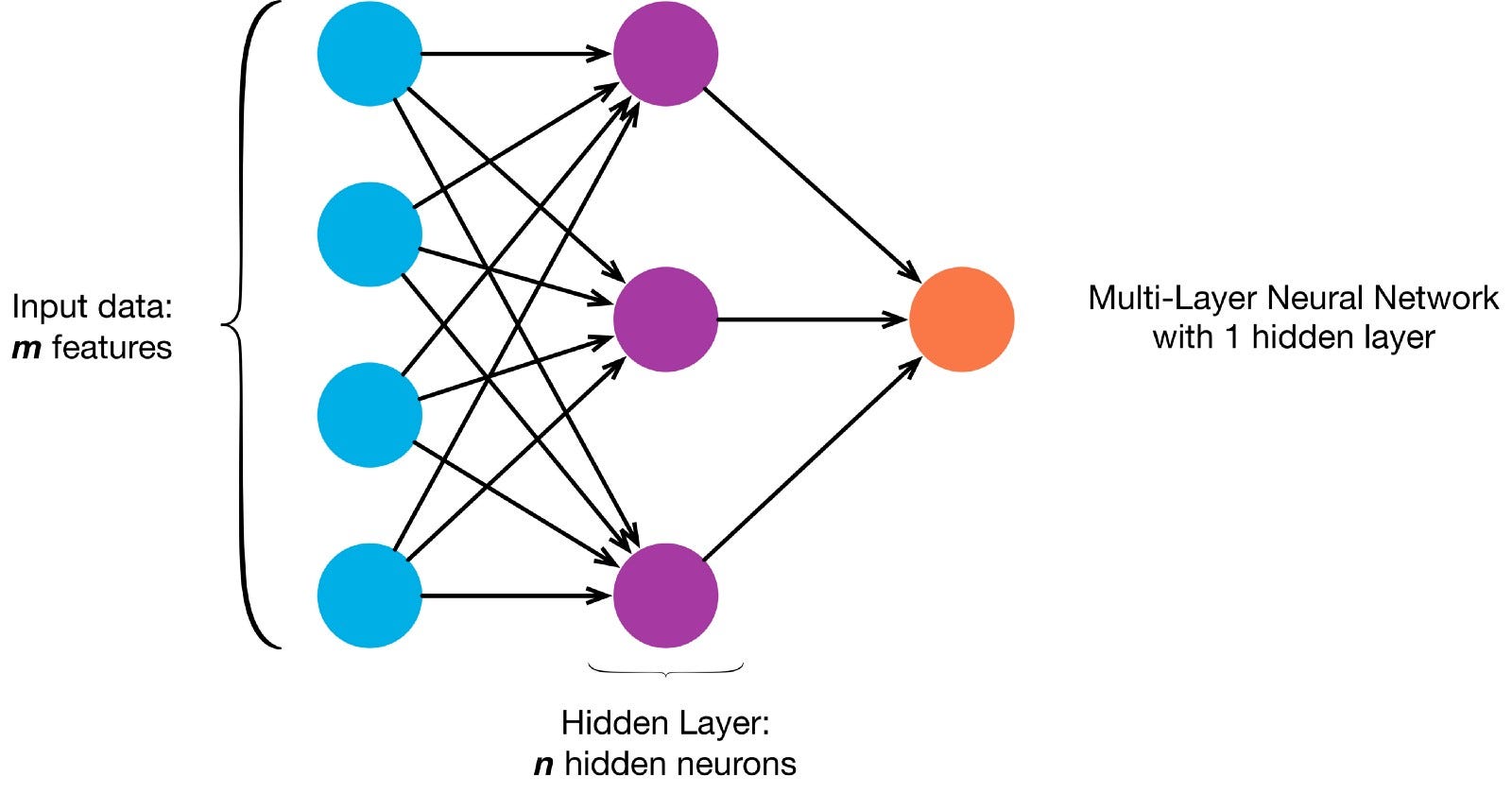
Der er typisk et inputlag (indeholdende et antal neuroner i det samme lag) > antallet af inputfunktioner i dataene), et outputlag (indeholdende et antal neuroner svarende til antallet af klasser) og et skjult lag (indeholdende et hvilket som helst antal neuroner).

der kan være mere end et skjult lag for at tillade det neurale net at lære mere komplekse beslutningsgrænser (enhver neural net med mere end et skjult lag betragtes som et dybt neuralt net).
lad os bygge en dyb NN for at male dette billede:

lad os hente i et array
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
nu lærer vores Ann at male er en overvåget læringsopgave, så vi er nødt til at oprette et mærket træningssæt (vores træningsdata vil have input og forventede OUTPUTETIKETTER for hver indgang). Træningsindgangene har 2 værdier(koordinaterne for hvert punkt).
i betragtning af billedets enkelhed kunne vi faktisk nærme os dette problem på en af to måder. Et klassificeringsproblem (hvor det neurale net forudsiger, om et punktpunkt hører til den” blå “klasse eller den” grå ” klasse, givet dens koordinater) eller et regressionsproblem (hvor det neurale net forudsiger RGB-værdier for et punktpunkt givet dets koordinater).
Hvis du behandler dette som et regressionsproblem: træningsudgangene har 3 værdier (de normaliserede R -, g -, b-værdier for hvert punkt). – Lad os bruge denne metode for nu.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
lad os nu oprette vores Ann:

- det skal have 2 neuroner i inputlaget (da der er 2 værdier at tage ind:& y koordinater).
- det skal have 3 neuroner i outputlaget (da der er 3 værdier at lære: r, g, b).
- antallet af skjulte lag og antallet af neuroner i hvert skjult lag er to hyperparametre at eksperimentere med (såvel som antallet af epoker, vi vil træne det til, aktiveringsfunktionen osv.) — Jeg bruger 10 skjulte lag med 100 neuroner i hvert skjult lag (hvilket gør dette til et dybt neuralt netværk)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
det uddannede netværk kan nu forudsige de normaliserede rgb-værdier for alle koordinater y = 1,1).
ann.predict(])
array(])
lad os bruge ANN til at forudsige rgb — værdierne for hver koordinat og lad os vise de forudsagte rgb-værdier for hele billedet for at se, hvor godt det gjorde (kvalitativt-vi skal forlade evalueringsmålinger til en anden tutorial)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

prøv at ændre hyperparametrene for at få bedre resultater.
Hvis vi i stedet for at behandle dette som et regressionsproblem behandler dette som et klassificeringsproblem, vil træningsudgangene have 2 værdier (sandsynlighederne for billedpunktet, der tilhører hver af de to klasser: “blå” og “grå”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
Vi kan genopbygge vores ANN som en binær klassifikator med 2 neuroner i inputlaget, 2 neuroner i outputlaget og 100 neuroner i det skjulte lag (med 10 skjulte lag)/p>
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
Vi kan nu bruge den trænede Ann til at forudsige den klasse, som hvert punkt tilhører (0: “grå” eller 1: “Blå”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: “grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

