Forståelse af dybe resterende netværk

dybe resterende netværk (ResNet) tog den dybe læringsverden med storm, da Microsoft Research frigav Dyb resterende læring til billedgenkendelse. Disse netværk førte til 1.plads vindende poster i alle fem hovedspor i ImageNet og COCO 2015 konkurrencer, der dækkede billedklassificering, objektdetektering og semantisk segmentering. Resnets robusthed er siden blevet bevist ved forskellige visuelle genkendelsesopgaver og ved ikke-visuelle opgaver, der involverer tale og sprog. Jeg brugte også ResNet ud over andre dybe læringsmodeller i min ph.d. – afhandling forskning.

dette indlæg opsummerer de tre papirer nedenfor, som alle er skrevet eller co-skrevet af Resnets opfinder Kaiming He, fordi jeg tror, at de originale papirer giver den mest intuitive og detaljerede forklaring af modellen / netværkene. Forhåbentlig kan dette indlæg hjælpe dig med at få en bedre forståelse af kernen i resterende netværk.

• Dyb Restlæring til billedgenkendelse
• Identitetskortlægninger i dybe Restnetværk
• aggregeret Resttransformation til dybe neurale netværk

Intuition på dybt Restnetværk (stackoverløb ref)

en restblok vises som følgende:

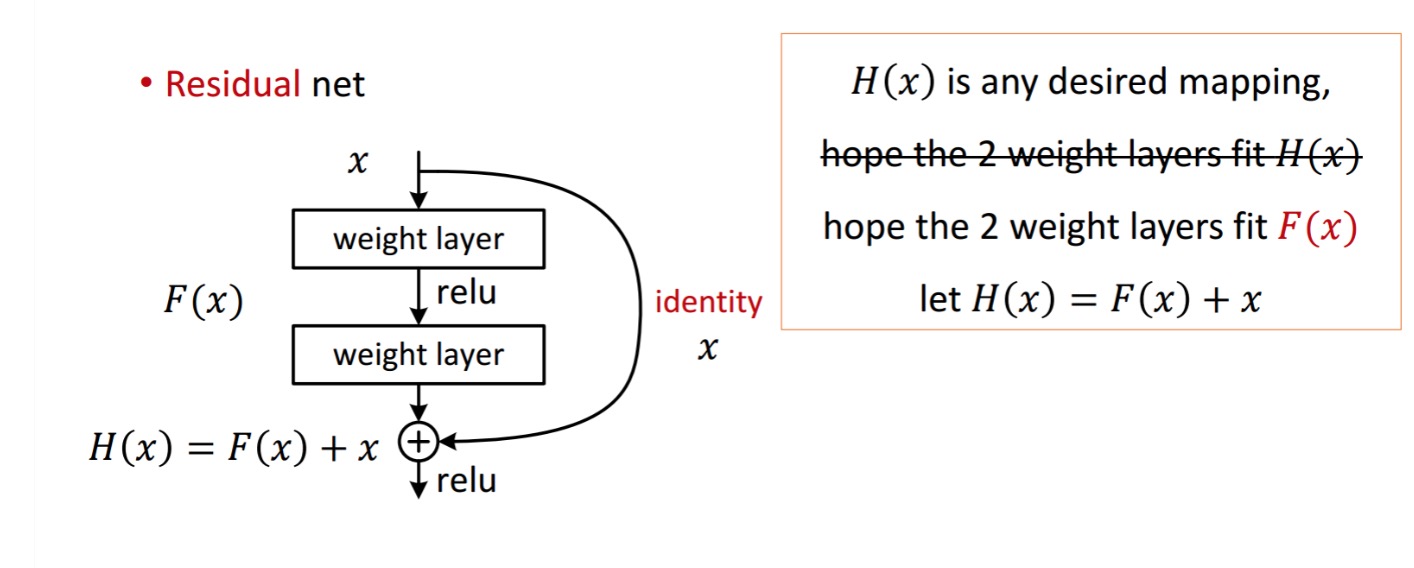
så den viste restenhed opnås ved behandling med to vægtlag. Så tilføjer det til at opnå . Antag nu, at det er dit ideelle forudsagte output, der matcher din grundsandhed. Da opnåelse af det ønskede afhænger af at få det perfekte . Det betyder, at de to vægtlag i den resterende enhed faktisk skal være i stand til at producere det ønskede , så er det garanteret at få det ideelle.

opnås som følger.

opnås som følger.

forfatterne antager, at den resterende kortlægning (dvs.) kan være lettere at optimere end. For at illustrere med et simpelt eksempel, antage, at den ideelle . Så for en direkte kortlægning ville det være svært at lære en identitetskortlægning, da der er en stak af ikke-lineære lag som følger.

så det ville være svært at tilnærme identitetskortlægningen med alle disse vægte og ReLUs i midten.

nu, hvis vi definerer den ønskede kortlægning , så skal vi bare få som følger.

at opnå ovenstående er let. Bare Indstil enhver vægt til nul, så får du en nuludgang. Tilføj tilbage, og du får din ønskede kortlægning.

Dyb Restlæring til billedgenkendelse

Problem

når dybere netværk begynder at konvergere, er et nedbrydningsproblem blevet udsat: med netværksdybden stigende bliver nøjagtigheden mættet og nedbrydes derefter hurtigt.

ser nedværdigende i aktion:

lad os tage et lavt netværk og dets dybere modstykke ved at tilføje flere lag til det.

værste tilfælde: Deeper models tidlige lag kan erstattes med lavt netværk, og de resterende lag kan bare fungere som en identitetsfunktion (Input svarende til output).

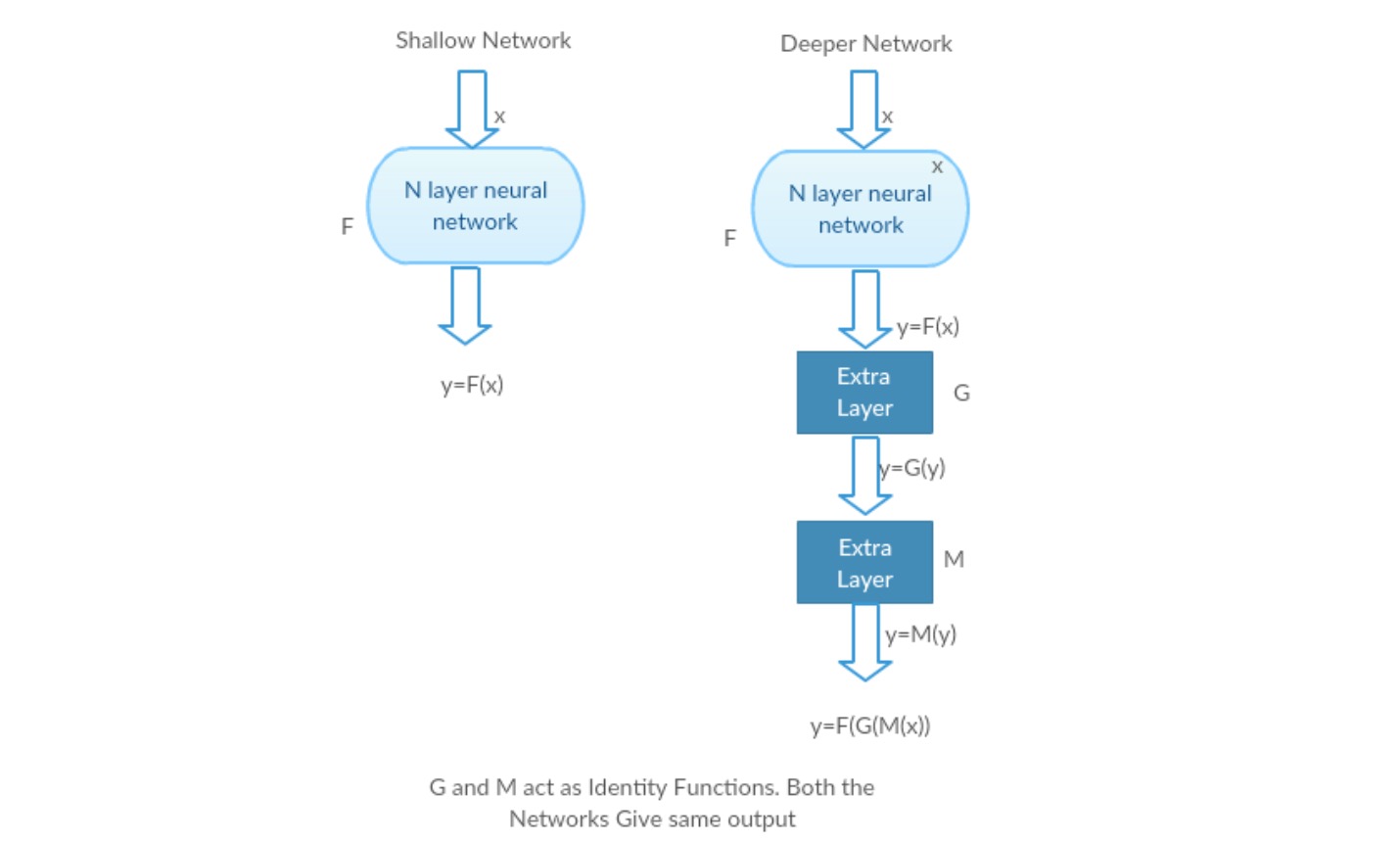
Belønningsscenarie: i det dybere netværk tilnærmer de ekstra lag bedre kortlægningen, end den er lavere moddel og reducerer fejlen med en betydelig margen.

eksperiment: I værste fald skal både det lave netværk og den dybere variant af det give den samme nøjagtighed. I belønningsscenariet skal den dybere model give bedre nøjagtighed, end den er lavere moddel. Men eksperimenter med vores nuværende løsere afslører, at dybere modeller ikke fungerer godt. Så brug af dybere netværk nedbryder modelens ydeevne. Disse papirer forsøger at løse dette problem ved hjælp af dybe resterende læringsrammer.

hvordan man løser?

i stedet for at lære en direkte kortlægning af med en funktion (et par stablede ikke-lineære lag). Lad os definere den resterende funktion ved hjælp af , som kan omformuleres til , hvor og repræsenterer de stablede ikke-lineære lag og identitetsfunktionen(input=output) henholdsvis.

forfatterens hypotese er, at det er let at optimere den resterende kortlægningsfunktion end at optimere den originale, ikke-refererede kortlægning .

Intuition bag resterende blokke:

lad os tage identitetskortlægningen som et eksempel (f.eks.). Hvis identitetskortlægningen er optimal, kan vi let skubbe resterne til nul () end at passe en identitetskortlægning () med en stak ikke-lineære lag. På simpelt sprog er det meget nemt at komme med en løsning som i stedet for at bruge stak af ikke-lineære cnn-lag som funktion (tænk over det). Så denne funktion er, hvad forfatterne kaldte resterende funktion.

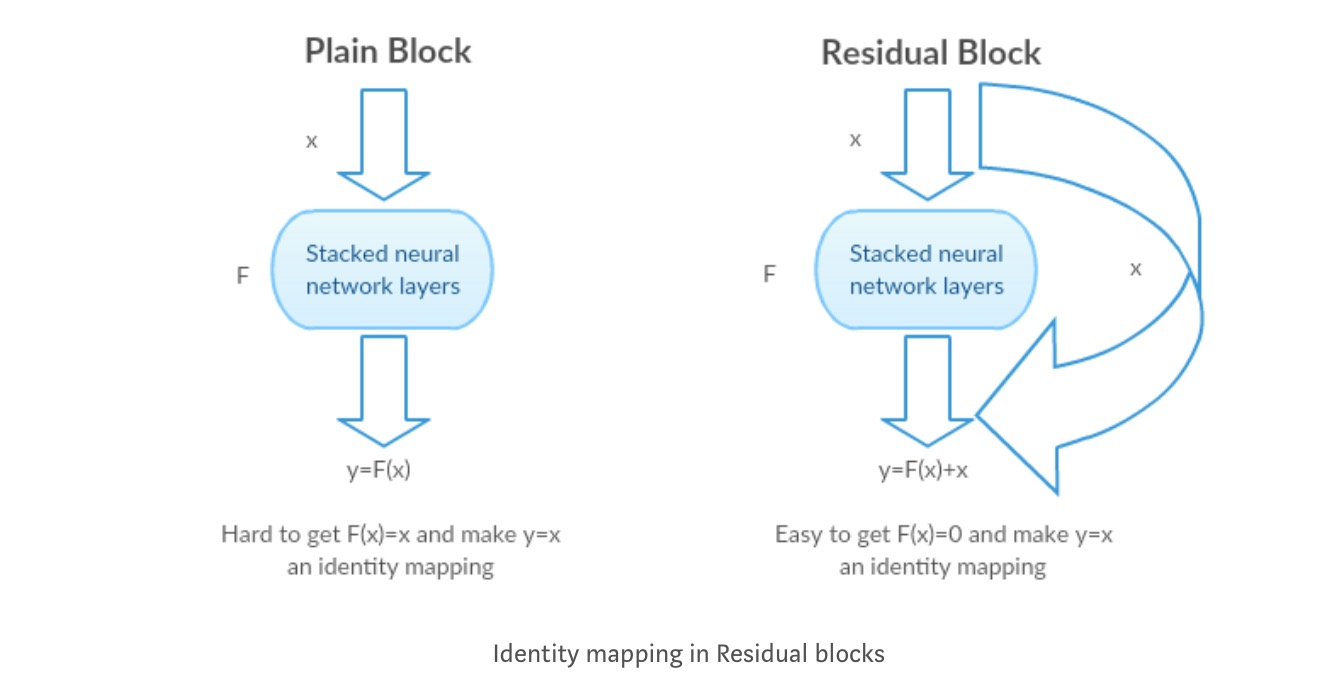
forfatterne lavede flere tests for at teste deres hypotese. Lad os se på hver af dem nu.

Test cases:

Tag et almindeligt netværk (VGG slags 18 lag netværk) (netværk-1) og en dybere variant af det (34-lag, netværk-2) og tilføj resterende lag til netværket-2 (34 lag med resterende forbindelser, netværk-3).

design af netværket:

1. brug 3*3 filtre for det meste.
2. ned prøveudtagning med CNN lag med stride 2.
3. globalt gennemsnitligt poollag og et 1000-vejs fuldt forbundet lag med Softmaks i slutningen.

Der er to slags resterende forbindelser:

I. identitetsgenveje () kan bruges direkte, når input () og output () har samme dimensioner.

II. når dimensionerne ændres, a) genvejen udfører stadig identitetskortlægning med ekstra nulindgange polstret med den øgede dimension. B) projektionsgenvejen bruges til at matche dimensionen (udført af 1*1 conv) ved hjælp af følgende formel

resultater

selvom 18-lagsnetværket kun er underrummet i 34-lagsnetværket, fungerer det stadig bedre. ResNet overgår med en betydelig margin, hvis netværket er dybere

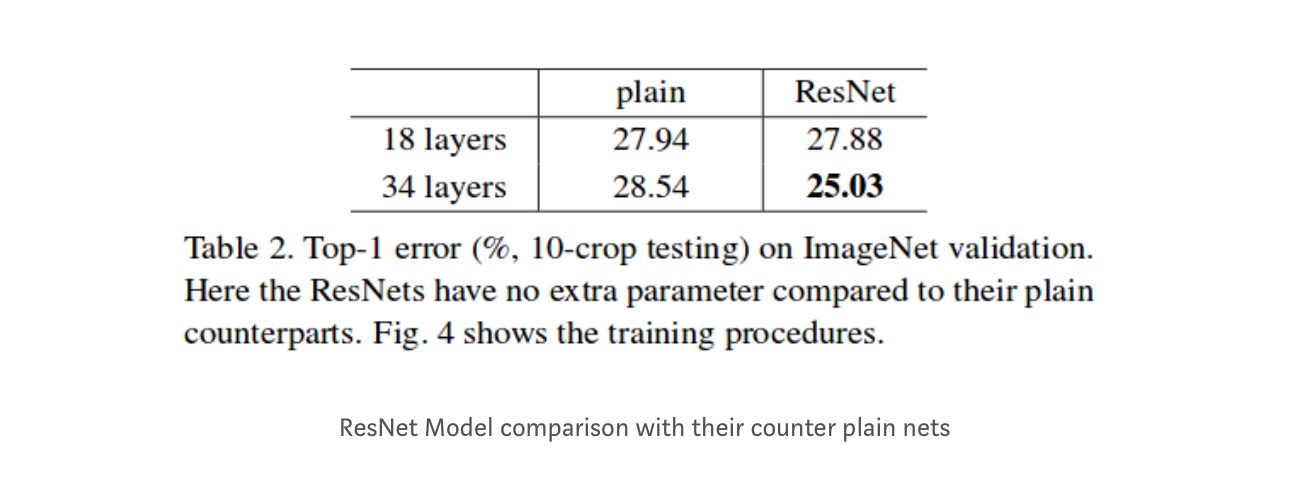
dybere studier

desuden studeres flere netværk:

hver ResNet-blok er enten 2-lags dyb (brugt til i små netværk som resnet 18, 34) eller 3 lag dyb( resnet 50, 101, 152).

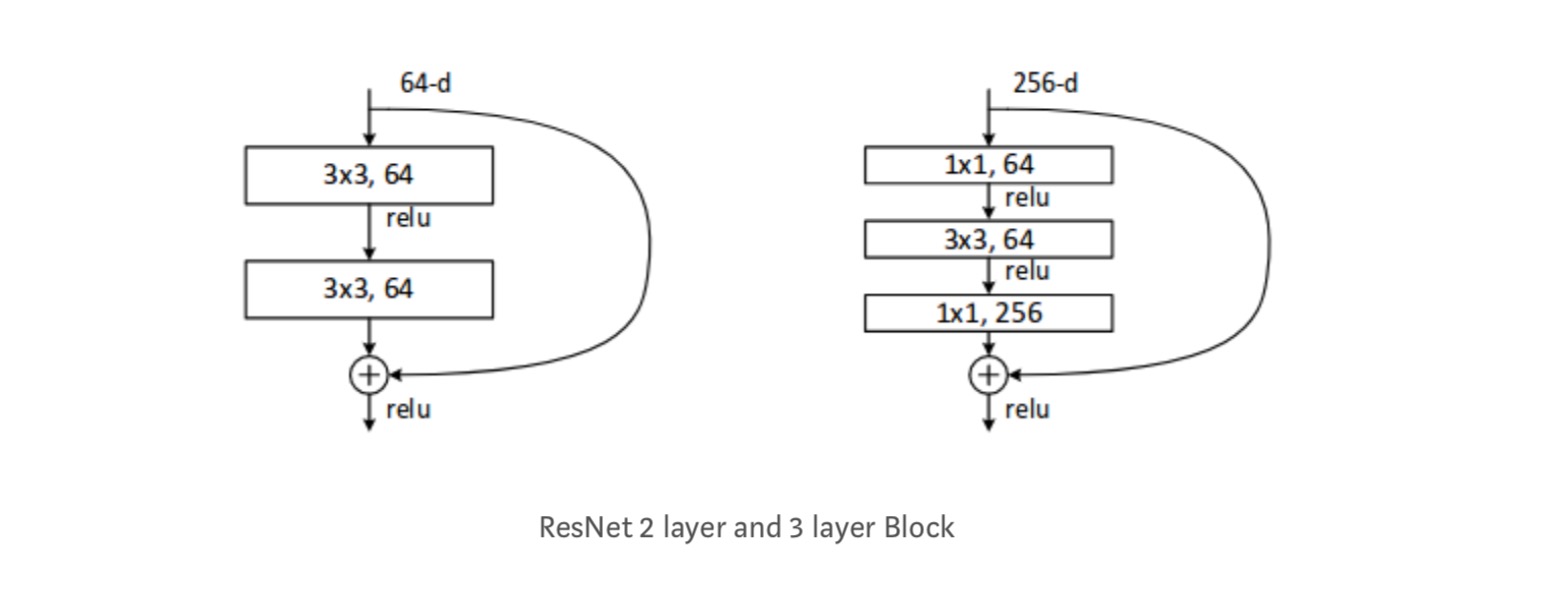
observationer

1. ResNet netværk konvergerer hurtigere i forhold til almindelig tæller del af det.
2. identitet vs projektion shorcuts. Meget små trinvise gevinster ved hjælp af projektionsgenveje (ligning-2) i alle lagene. Så alle ResNet-blokke bruger kun Identitetsgenveje med fremskrivninger, der kun bruges, når dimensionerne ændres.
3. ResNet-34 opnåede en top-5 valideringsfejl på 5,71% bedre end BN-inception og VGG. ResNet-152 opnår en top-5 valideringsfejl på 4,49%. Et ensemble på 6 modeller med forskellige dybder opnår en top-5 valideringsfejl på 3,57%. Vinder 1. pladsen i ILSVRC-2015

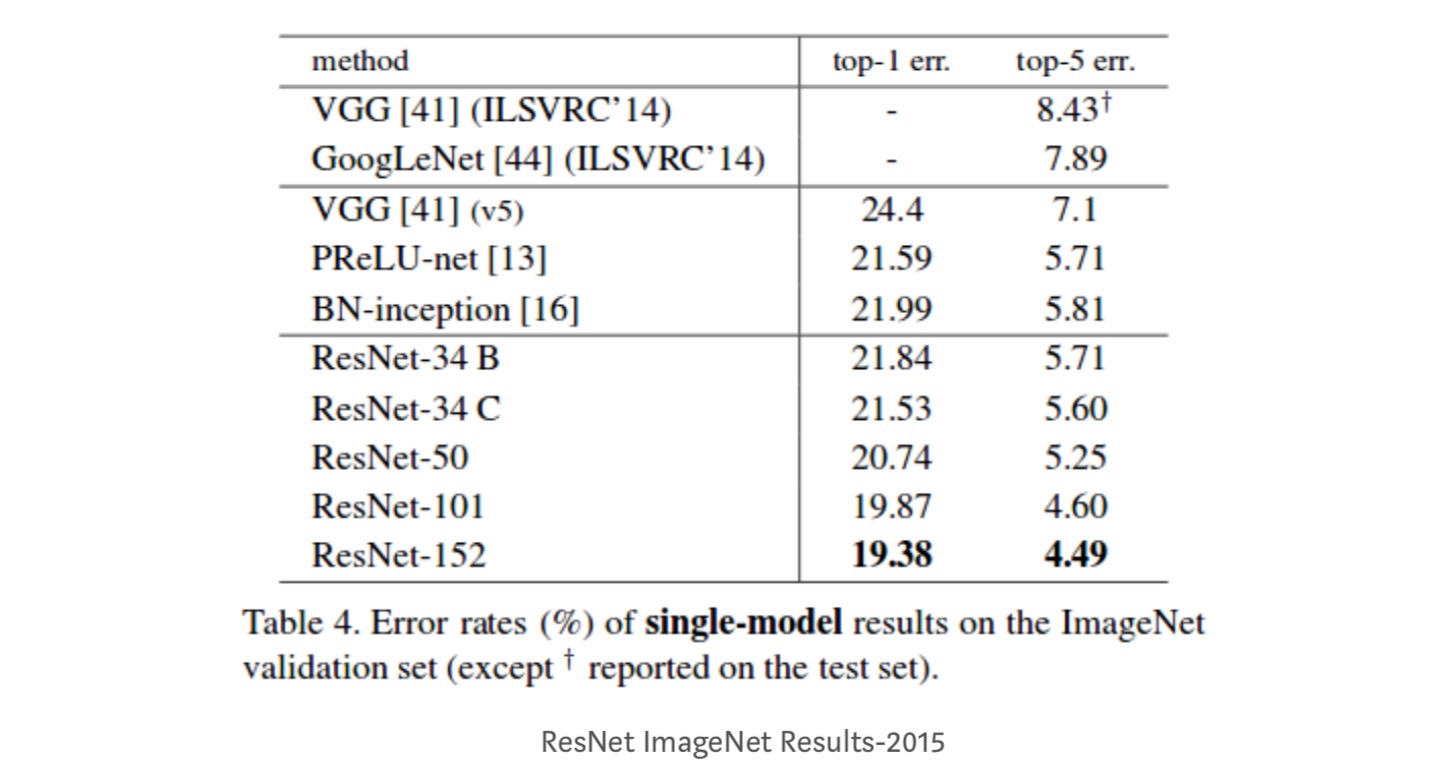
identitetskort i dybe resterende netværk

dette papir giver den teoretiske forståelse af, hvorfor forsvindende gradientproblem ikke er til stede i resterende netværk og rollen som springforbindelser (springforbindelser betyder input eller ) ved at erstatte Identitetskortlægning (h) med forskellige funktioner.

introduktion

dybe resterende netværk består af mange stablede “resterende enheder”. Hver enhed kan udtrykkes i en generel form:

hvor og er input og output af enheden, og er en restfunktion. I det sidste papir, er en identitet kortlægning og er en ReLU funktion.

den centrale ide med ResNets er at lære den additive restfunktion med hensyn til , med et nøglevalg at bruge en identitetskortlægning . Dette realiseres ved at vedhæfte en identity skip-forbindelse (“genvej”).

i dette papir analyserer vi dybe resterende netværk ved at fokusere på at skabe en “direkte” sti til udbredelse af information — ikke kun inden for en resterende enhed, men gennem hele netværket. Vores afledninger afslører, at hvis begge og er identitetskortlægninger, signalet kunne forplantes direkte fra en enhed til andre enheder, i både fremad og bagud. Vores eksperimenter viser empirisk, at træning generelt bliver lettere, når arkitekturen er tættere på ovenstående to betingelser.

for at forstå rollen som springforbindelser analyserer og sammenligner vi forskellige typer af . Vi finder ud af, at den identitetskortlægning, der er valgt i det sidste papir , opnår den hurtigste fejlreduktion og laveste træningstab blandt alle varianter, vi undersøgte, der henviser til, at springforbindelser af skalering, gating, og 1 til 1 vindinger alle fører til højere træningstab og fejl. Disse eksperimenter antyder, at det er nyttigt at holde en “ren” informationssti til at lette optimeringen.

for at konstruere en identitetskortlægning ser vi aktiveringsfunktionerne (ReLU og BN) som “foraktivering” af vægtlagene i modsætning til konventionel visdom om “postaktivering”. Dette synspunkt fører til et nyt resterende enhedsdesign, vist i den følgende figur. Baseret på denne enhed præsenterer vi konkurrencedygtige resultater på CIFAR-10/100 med et 1001-lag ResNet, som er meget lettere at træne og generaliserer bedre end det originale ResNet. Vi rapporterer yderligere forbedrede resultater på ImageNet ved hjælp af et 200-lags ResNet, for hvilket modstykket til det sidste papir begynder at overfit. Disse resultater antyder, at der er meget plads til at udnytte dimensionen af netværksdybde, en nøgle til succes med moderne dyb læring.

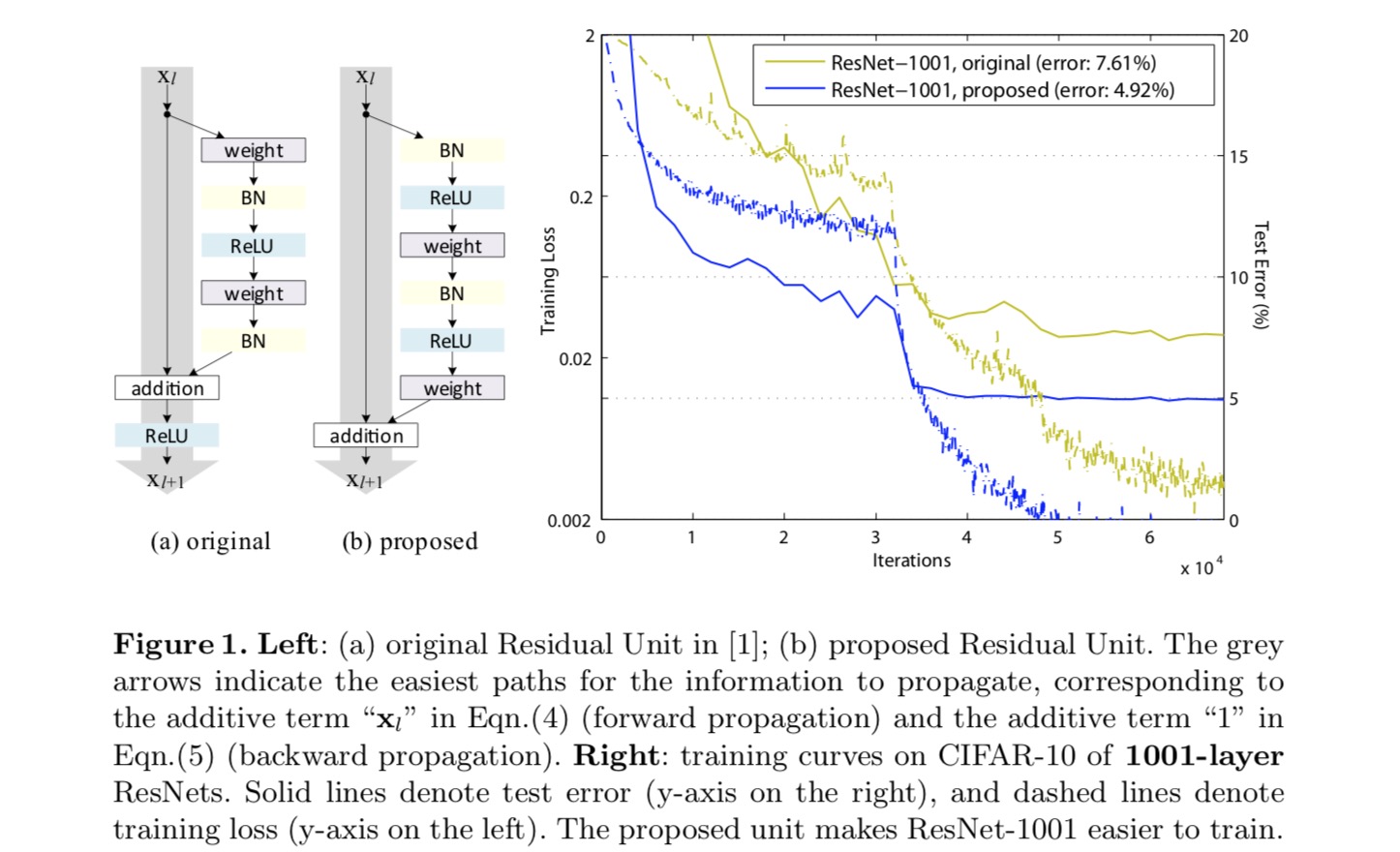
analyse af dybe resterende netværk

ResNets udviklet i det sidste papir er modulariserede arkitekturer, der stabler byggesten med samme forbindelsesform. I dette papir kalder vi disse blokke “resterende enheder”. Den oprindelige Restenhed i det sidste papir udfører følgende beregning:

Her er indtastningsfunktionen til den resterende enhed. er et sæt vægte ( og forstyrrelser) forbundet med den resterende enhed, og er antallet af lag i en resterende enhed (er 2 eller 3 i det sidste papir). angiver den resterende funktion, e.g., en stak med to 3-3-3-konvolutlag i det sidste papir. Funktionen er operationen efter elementvis Tilføjelse, og i det sidste papir er ReLU. Funktionen er indstillet som en identitetskortlægning: .

IF er også en identitetskortlægning:, vi kan få:

rekursivt vil vi have:

for enhver dybere enhed og enhver lavere enhed . Denne ligning udviser nogle pæneegenskaber. (1) træk ved enhver dybere enhed kan repræsenteres som træk ved enhver lavere enhed plus en restfunktion i en form for , hvilket indikerer, at modellen er på en resterende måde mellem enhver enhed og . (2) funktionen for enhver dyb enhed er summen af output fra alle foregående restfunktioner (plus). Dette er i modsætning til et “almindeligt netværk”, hvor en funktion er en serie af matrice-vektorprodukter, siger (ignorerer BN og ReLU).

ovenstående ligning fører også til pæne bagudgående udbredelsesegenskaber. Betegner tabsfunktionen som fra kædereglen for backpropagation har vi:

ovenstående ligning indikerer, at gradienten kan nedbrydes i to additive termer: et udtryk for, at formerer oplysninger direkte uden om nogen vægt lag, og en anden betegnelse for, at formerer sig gennem vægt lag. Additivbetegnelsen for sikrer, at information direkte formeres tilbage til enhver lavere Enhed l. ovenstående ligning antyder også, at det er usandsynligt, at gradienten annulleres for en mini-batch, fordi udtrykket generelt ikke altid kan være -1 for alle prøver i en mini-batch. Dette indebærer, at gradienten af et lag ikke forsvinder, selv når vægten er vilkårligt lille.

ovenstående to ligninger antyder, at signalet kan forplantes direkte fra en hvilken som helst enhed til en anden, både fremad og bagud. Grundlaget for den første ovenstående to ligninger er to identitetskortlægninger: (1) identity skip-forbindelsen og (2) betingelsen , der er en identitetskortlægning.

betydningen af identity skip connections

lad os overveje en simpel ændring, , for at bryde identitetsgenvejen:

hvor er en modulerende skalar (for enkelhed antager vi stadig identitet). Rekursivt anvendelse af denne formulering opnår vi en ligning svarende til ovenstående:

hvor notationen absorberer skalarerne i de resterende funktioner. Tilsvarende har vi backpropagation af følgende form:

I modsætning til den foregående ligning moduleres det første additive udtryk i denne ligning med en faktor . For et ekstremt dybt netværk (er stort), hvis for alle , kan denne faktor være eksponentielt stor; hvis for alle , kan denne faktor være eksponentielt lille og forsvinde, hvilket blokerer det backpropagerede signal fra genvejen og tvinger det til at strømme gennem vægtlagene. Dette resulterer i optimeringsvanskeligheder, som vi viser ved eksperimenter.

i ovenstående analyse erstattes den oprindelige identity skip-forbindelse med en simpel skalering . Hvis skip-forbindelsen repræsenterer mere komplicerede transformationer (såsom gating og 1 liter 1 vindinger), i ovenstående ligning bliver det første udtryk, hvor er derivatet af . Dette produkt kan også hindre informationsformidling og hæmme træningsproceduren, som det fremgår af de følgende eksperimenter.

eksperimenter på Springforbindelser

vi eksperimenterer med 110-lags ResNet på CIFAR-10. Denne ekstremt dybe ResNet – 110 har 54 to-lags resterende enheder (bestående af 3 liter 3 konvolutionslag) og er udfordrende for optimering. Forskellige typer springforbindelser eksperimenteres. Se følgende figur:

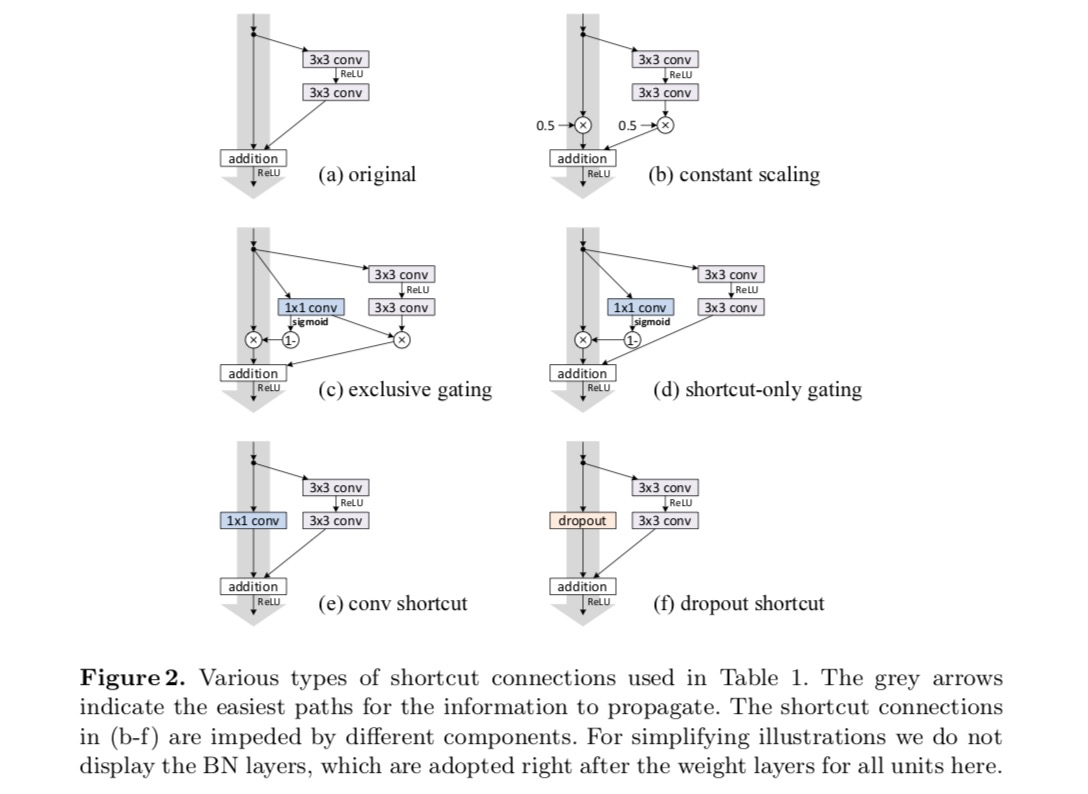
klassificeringsresultaterne vises i følgende tabel:

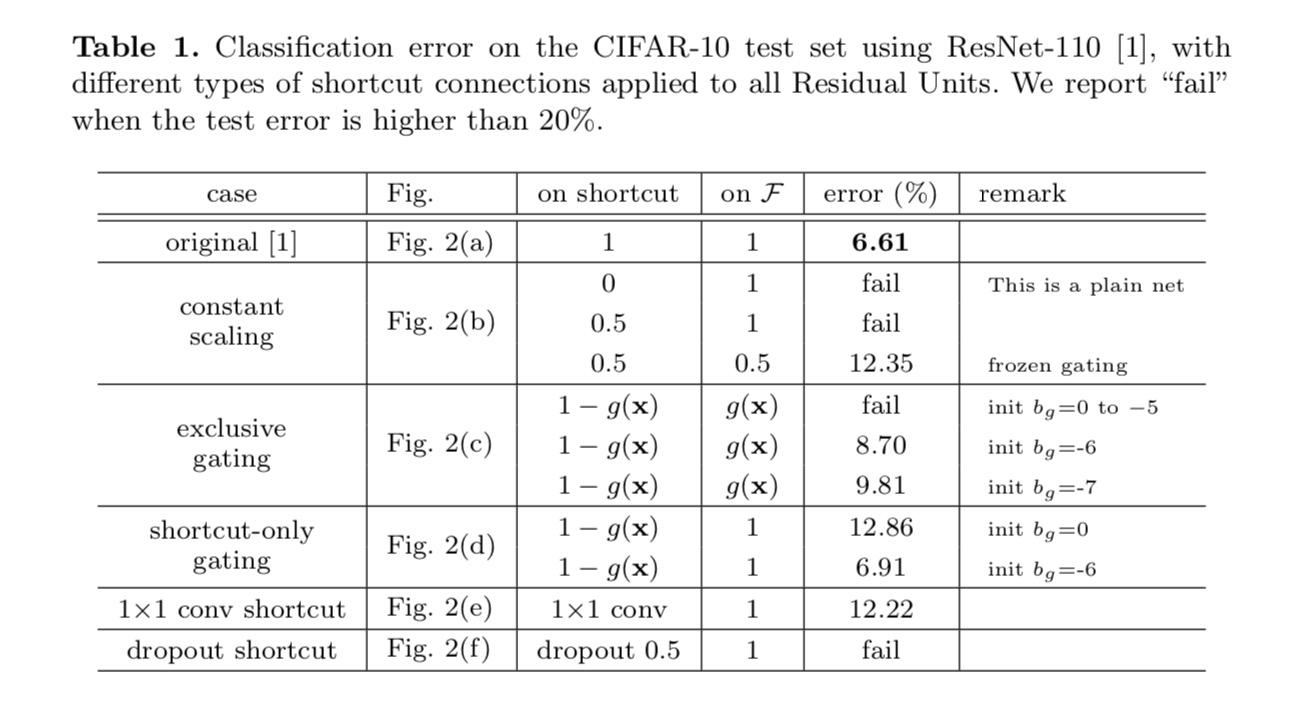
som angivet med de grå pile i ovenstående figur er genvejsforbindelserne de mest direkte stier for informationen at udbrede. Multiplikative manipulationer (skalering, gating, 1 til 1 vindinger og frafald) på genveje kan hæmme informationsudbredelse og føre til optimeringsproblemer.

det er bemærkelsesværdigt, at gating-og 1-venstre 1-konvolutionsgenveje introducerer flere parametre og bør have stærkere repræsentationsevner end identitetsgenveje. Faktisk dækker genvejsgenvejen kun gating og 1 tir 1 convolution løsningsrummet for identitetsgenveje (dvs.de kunne optimeres som identitetsgenveje). Imidlertid er deres træningsfejl højere end identitetsgenveje, hvilket indikerer, at nedbrydningen af disse modeller skyldes optimeringsproblemer i stedet for repræsentative evner.

anvendelse af aktiveringsfunktioner

eksperimenter i ovenstående afsnit er under den antagelse, at aktiveringen efter tilsætning er identitetskortlægningen. Men i ovenstående eksperimenter er ReLU som designet i det første papir. Dernæst undersøger vi virkningen af .

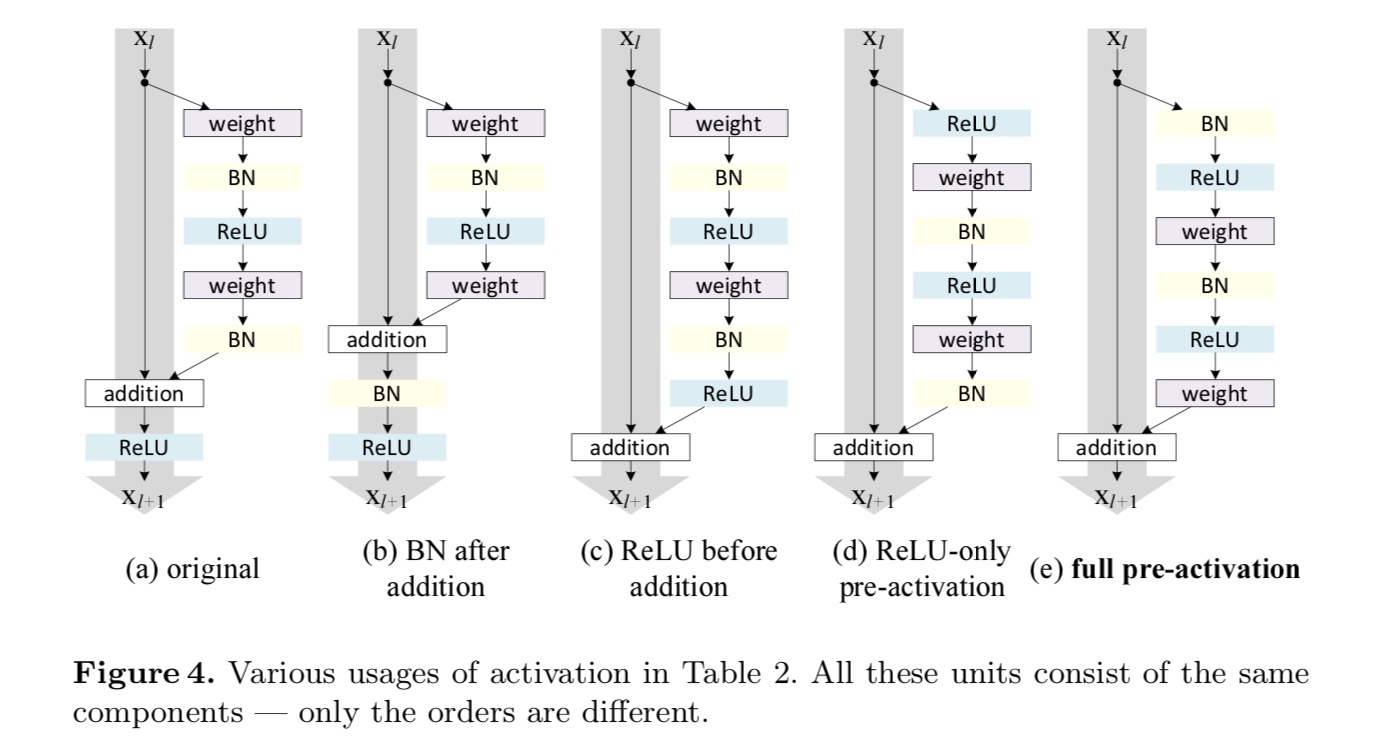
Vi ønsker at lave en identitetskortlægning, som gøres ved at omarrangere aktiveringsfunktionerne (ReLU og/eller BN, batch normalisering). I den følgende figur har den originale Restenhed i det sidste papir en form i Fig. 4 (A) – BN anvendes efter hvert vægtlag, og ReLU vedtages efter BN bortset fra at den sidste ReLU i en Restenhed er efter elementvis tilsætning ( = ReLU). Fig. 4 (b-e) vis de alternativer, vi undersøgte.

eksperimenter med aktivering

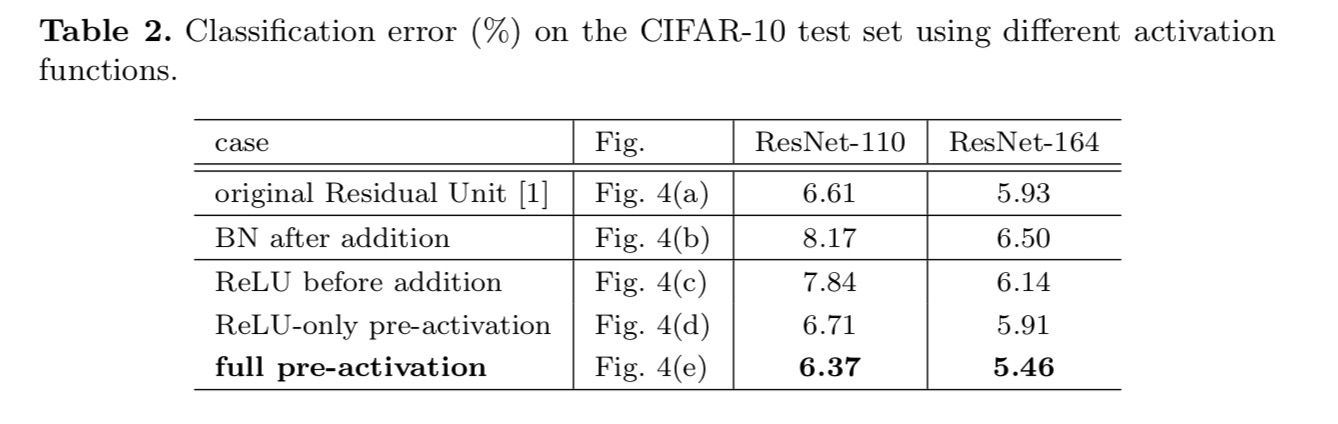
i dette afsnit eksperimenterer vi med ResNet-110 og en 164-lags Flaskehalsarkitektur (betegnet som ResNet-164). En flaskehals resterende enhed består af en 1 liter 1 lag for at reducere dimension, en 3 liter 3 lag, og en 1 liter 1 lag for at genoprette dimension. Som designet i det sidste papir svarer dens beregningskompleksitet til den resterende enhed med to-3 liter 3.

Post-aktivering eller pre-aktivering?

i det oprindelige design påvirker aktiveringen begge stier i den næste resterende enhed: . Dernæst udvikler vi en asymmetrisk form , hvor en aktivering kun påvirker stien:, for enhver . Ved at omdøbe notationerne har vi følgende form:

for denne nye Restenhed som i ovenstående ligning bliver den nye aktivering efter tilføjelse en identitetskortlægning. Dette design betyder, at hvis en ny aktivering efter tilsætning vedtages asymmetrisk, svarer det til omarbejdning som foraktivering af den næste Restenhed. Dette er illustreret i følgende figur:

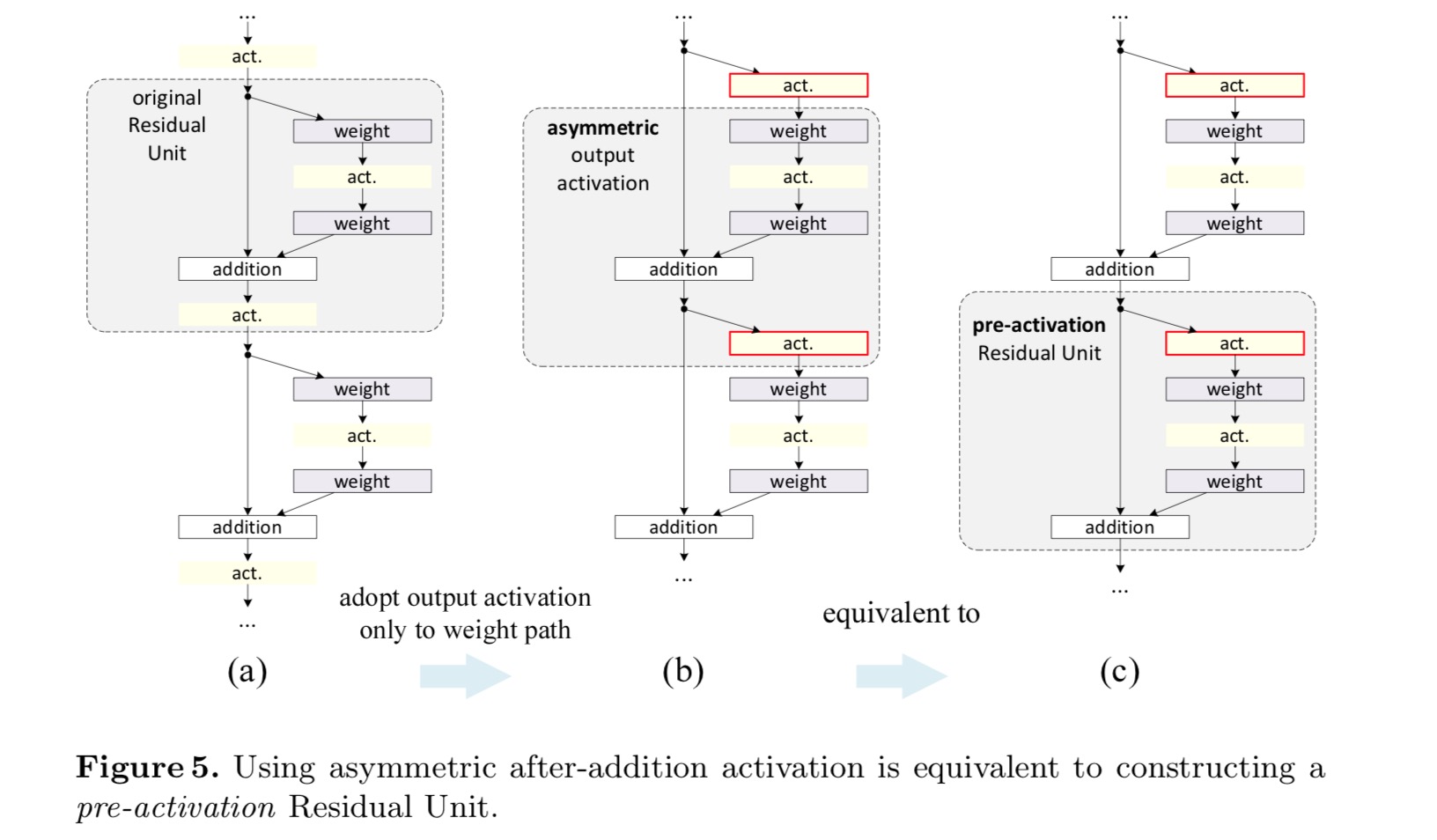
sondringen mellem post-aktivering / pre-aktivering skyldes tilstedeværelsen af den elementvise tilsætning. For et almindeligt netværk, der har n − lag, er der N – 1-aktiveringer (BN/ReLU), og det er ligegyldigt, om vi tænker på dem som post-eller pre-aktiveringer. Men for forgrenede lag fusioneret ved tilsætning betyder aktiveringspositionen noget. De forskellige anvendelser af aktivering vises i figur 4.

vi eksperimenterer med to sådanne designs: (1) ReLU-only pre-activation og (2) fuld pre-activation, hvor BN og ReLU begge er vedtaget før vægtlag. På en eller anden måde overraskende, når BN og ReLU begge bruges som foraktivering, forbedres resultaterne med sunde margener

Vi finder virkningen af foraktivering er dobbelt. For det første bliver optimeringen yderligere lettet (sammenlignet med baseline ResNet), fordi f er en identitetskortlægning. For det andet forbedrer brugen af BN som foraktivering reguleringen af modellerne.

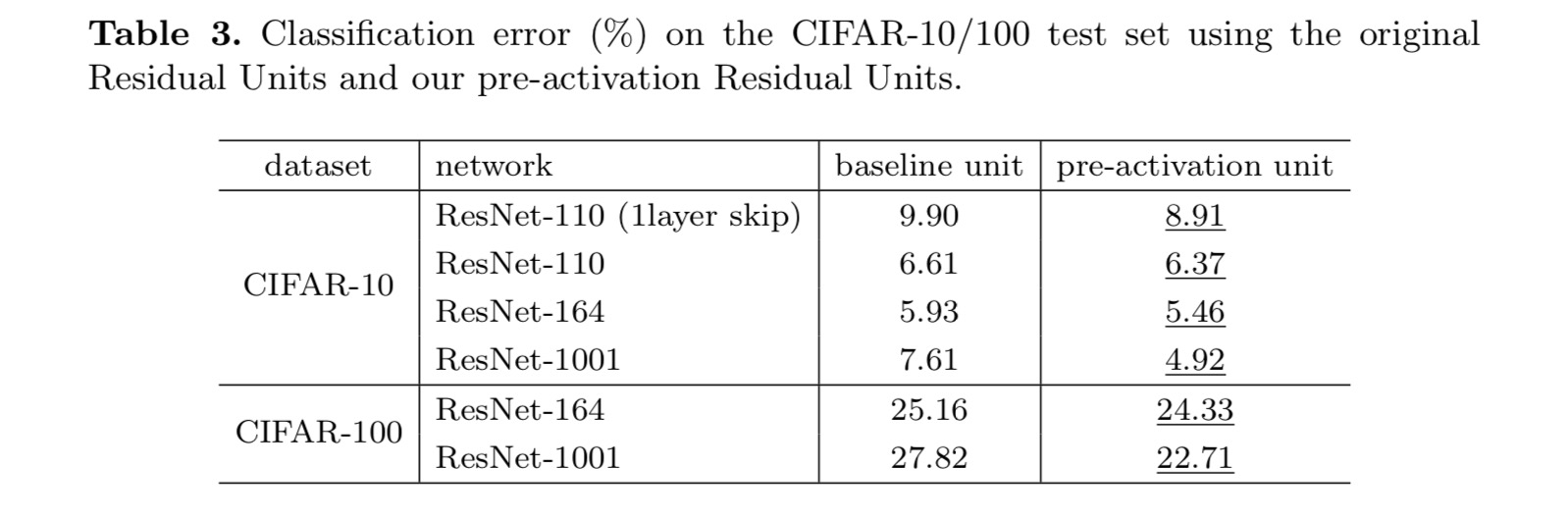
konklusion

dette papir undersøger formeringsformuleringerne bag forbindelsesmekanismerne for dybe resterende netværk. Vores afledninger indebærer, at identitetsgenvejsforbindelser og aktivering af identitet efter tilsætning er afgørende for at gøre informationsudbredelse glat. Ablationseksperimenter demonstrerer phenom – ena, der er i overensstemmelse med vores afledninger. Vi præsenterer også 1000-lags dybe netværk, der let kan trænes og opnå forbedret nøjagtighed.

aggregeret Resttransformation til dybe neurale netværk

introduktion

forskning i visuel genkendelse gennemgår en overgang fra “funktionsteknik” til “netværksteknik”. Menneskelig indsats er blevet flyttet til at designe bedre netværksarkitekturer til læringsrepræsentationer.

design af arkitekturer bliver stadig vanskeligere med det stigende antal hyper-parametre, især når der er mange lag. VGG-nets udviser en enkel, men effektiv strategi for at konstruere meget dybe netværk: stabling af byggesten i samme form. Denne strategi er arvet af ResNets, som stabler moduler af samme topologi. Denne enkle regel reducerer de frie valg af hyperparametre, og dybden udsættes som en væsentlig dimension i neurale netværk. Desuden hævder vi, at enkelheden i denne regel kan reducere risikoen for overtilpasning af hyperparametrene til et specifikt datasæt. Robustheden af VGG-nets og ResNets er blevet bevist ved forskellige visuelle genkendelsesopgaver og ved ikke-visuelle opgaver, der involverer tale og sprog.

I modsætning til VGG-nets har familien af startmodeller vist, at omhyggeligt designede topologier er i stand til at opnå overbevisende nøjagtighed med lav teoretisk kompleksitet. Startmodellerne har udviklet sig over tid, men en vigtig fælles ejendom er en split-transform-merge-strategi. I et Startmodul er indgangen opdelt i et par lavere dimensionelle indlejringer (med 1 liter 1 vindinger), transformeret af et sæt specialiserede filtre (3 liter 3, 5 liter 5 osv.), og fusioneret ved sammenkædning. Det split-transform-merge opførsel af Startmoduler forventes at nærme sig repræsentationskraften i store og tætte lag, men med en betydeligt lavere beregningskompleksitet.

På trods af god nøjagtighed er realiseringen af startmodeller ledsaget af en række komplicerende faktorer. Selvom omhyggelige kombinationer af disse komponenter giver fremragende neurale netværksopskrifter, er det generelt uklart, hvordan man tilpasser Startarkitekturerne til nye datasæt/opgaver, især når der er mange faktorer og hyperparametre, der skal designes.

i dette papir præsenterer vi en simpel arkitektur, der vedtager VGG / ResNets’ strategi om at gentage lag, samtidig med at man udnytter split-transform-merge-strategien på en let, udvidelig måde. Et modul i vores netværk udfører et sæt transformationer, hver på en lavdimensionel indlejring, hvis output aggregeres ved summering. Vi forfølger en simpel realisering af denne ide — de transformationer, der skal aggregeres, er alle af samme topologi. Dette design giver os mulighed for at udvide til ethvert stort antal transformationer uden specialiserede designs.

Vi viser empirisk, at vores aggregerede transformationer overgår det originale ResNet-modul, selv under den begrænsede betingelse for at opretholde beregningskompleksitet og modelstørrelse. Vi understreger, at selvom det er relativt let at øge nøjagtigheden ved at øge kapaciteten (gå dybere eller bredere), er metoder, der øger nøjagtigheden, mens de opretholder (eller reducerer) kompleksitet, sjældne i litteraturen.

vores metode indikerer, at kardinalitet (størrelsen af sæt af transformationer) er en konkret, målbar dimension, der er af central betydning, ud over dimensionerne af bredde og dybde. Eksperimenter viser, at stigende kardinalitet er en mere effektiv måde at opnå nøjagtighed på end at gå dybere eller bredere, især når dybde og bredde begynder at give faldende afkast for eksisterende modeller.

vores neurale netværk, der hedder Resnæste (foreslår den næste dimension), overgår ResNet-101/152, ResNet-200, Inception-v3 og Inception-ResNet-v2 på ImageNet-klassificeringsdatasættet. Især er en 101-lags Resnæste i stand til at opnå bedre nøjagtighed end ResNet-200, men har kun 50% kompleksitet. Desuden udviser Resnæste betydeligt enklere design end alle startmodeller.

metode

Vi vedtager et stærkt modulariseret design efter VGG / ResNets. Vores netværk består af en stak resterende blokke. Disse blokke har samme topologi og er underlagt to enkle regler inspireret af VGG/ResNets: (1) hvis der produceres rumlige kort af samme størrelse, deler blokkene de samme hyperparametre (bredde og filterstørrelser), og (2) hver gang det rumlige kort nedprøves med en faktor 2, multipliceres blokkenes bredde med en faktor 2. Den anden regel sikrer, at beregningskompleksiteten med hensyn til FLOPs (flydende punktoperationer i #af multiplicer-tilføjer) er omtrent den samme for alle blokke.

med disse to regler behøver vi kun at designe et skabelonmodul, og alle moduler i et netværk kan bestemmes i overensstemmelse hermed. Så disse to regler indsnævrer designrummet meget og giver os mulighed for at fokusere på et par nøglefaktorer. De netværk, der er opbygget efter disse regler, er i tabel 1.

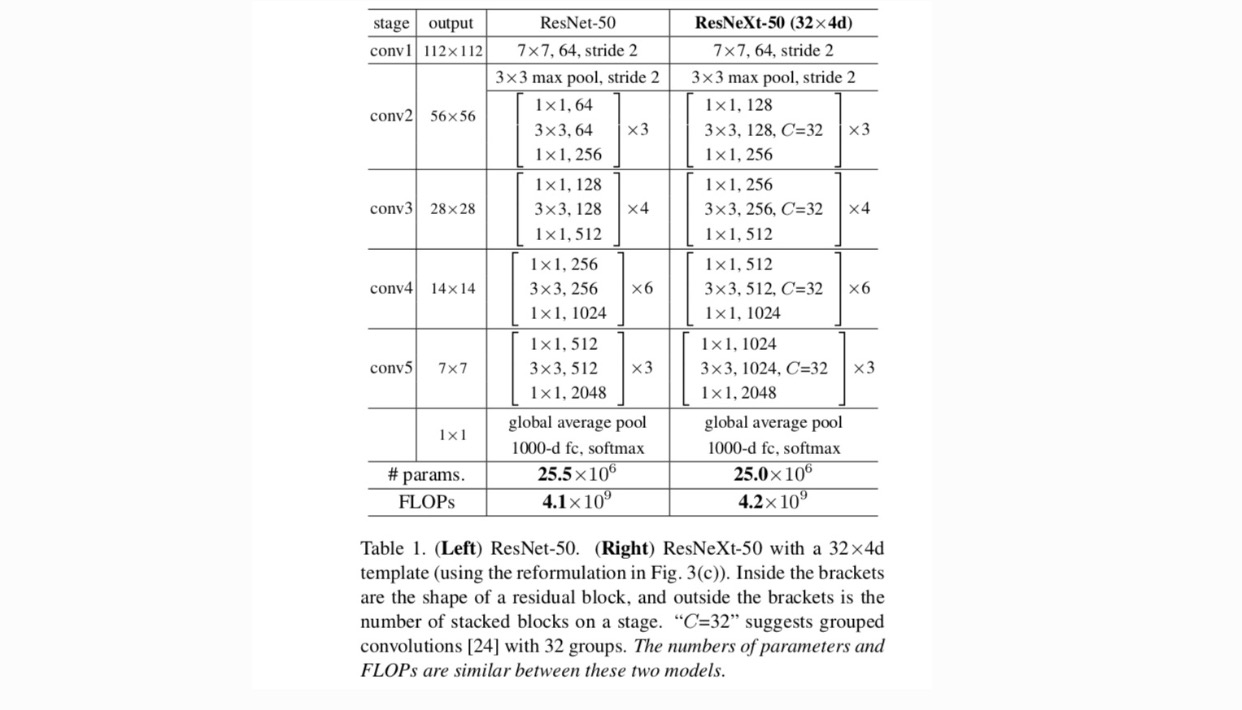
de enkleste neuroner i kunstige neurale netværk udfører indre produkt (vægtet sum), som er den elementære transformation udført af fuldt forbundne og indviklede lag.

ovenstående operation kan omarbejdes som en kombination af opdeling, transformation og aggregering. (1): opdeling: vektoren er skåret som en lavdimensionel indlejring, og i ovenstående er det et underrum med en enkelt dimension (2) Transformering: den lavdimensionelle repræsentation transformeres, og i ovenstående skaleres den simpelthen: (3) aggregering: transformationerne i alle indlejringer aggregeres af .

i betragtning af ovenstående analyse af en simpel neuron overvejer vi at erstatte den elementære transformation (v_i, h_i) med en mere generisk funktion, som i sig selv også kan være et netværk. Formelt præsenterer vi aggregerede transformationer som:

hvor kan være en vilkårlig funktion. Analogt med en simpel neuron, bør projicere i en (eventuelt lavdimensionel) indlejring og derefter omdanne den.

Vi henviser til kardinalitet. er i en position svarende til i, men behøver ikke lige og kan være et vilkårligt antal. Vi viser ved eksperimenter, at kardinalitet er en væsentlig dimension og kan være mere effektiv end dimensionerne af bredde og dybde.

i dette papir overvejer vi en enkel måde at designe transformationsfunktionerne på: alle har samme topologi. Dette udvider VGG-stil strategi for at gentage lag af samme form. Vi indstiller den individuelle transformation til at være den flaskehalsformede arkitektur illustreret i Fig. 1 (højre). I dette tilfælde producerer det første 1 liter 1 lag i hver den lavdimensionelle indlejring.

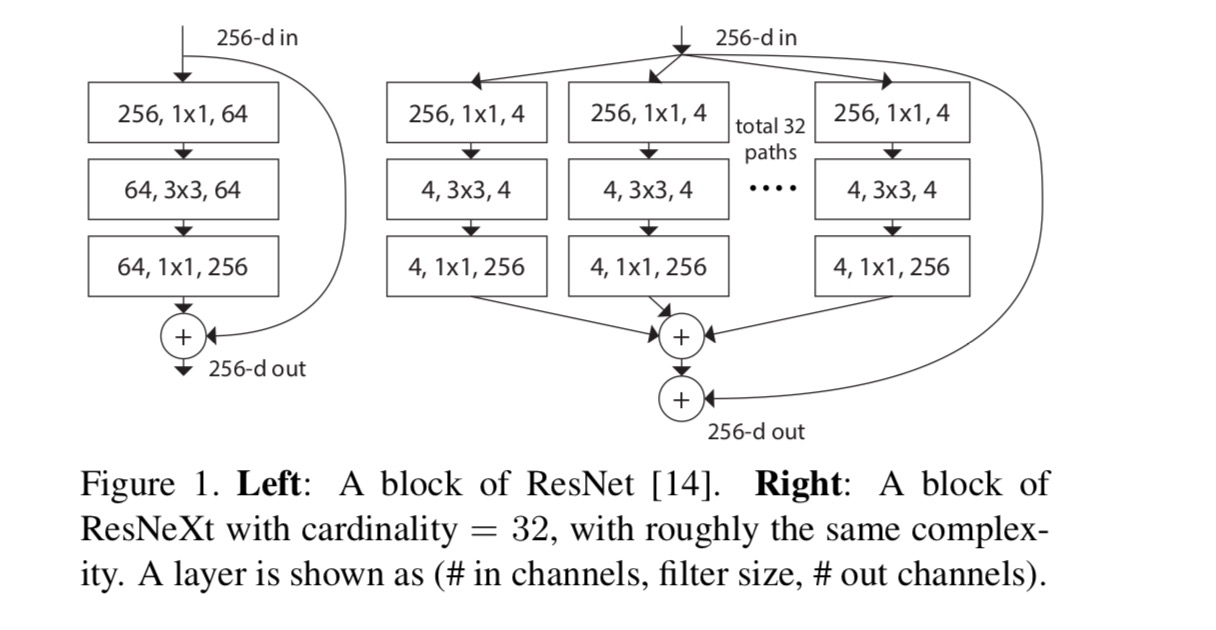
den aggregerede transformation i sidste ligning tjener som restfunktionen:

hvor er output.

forholdet mellem Resnæste og Inception-ResNet / grupperet-vindinger er vist i følgende figur:

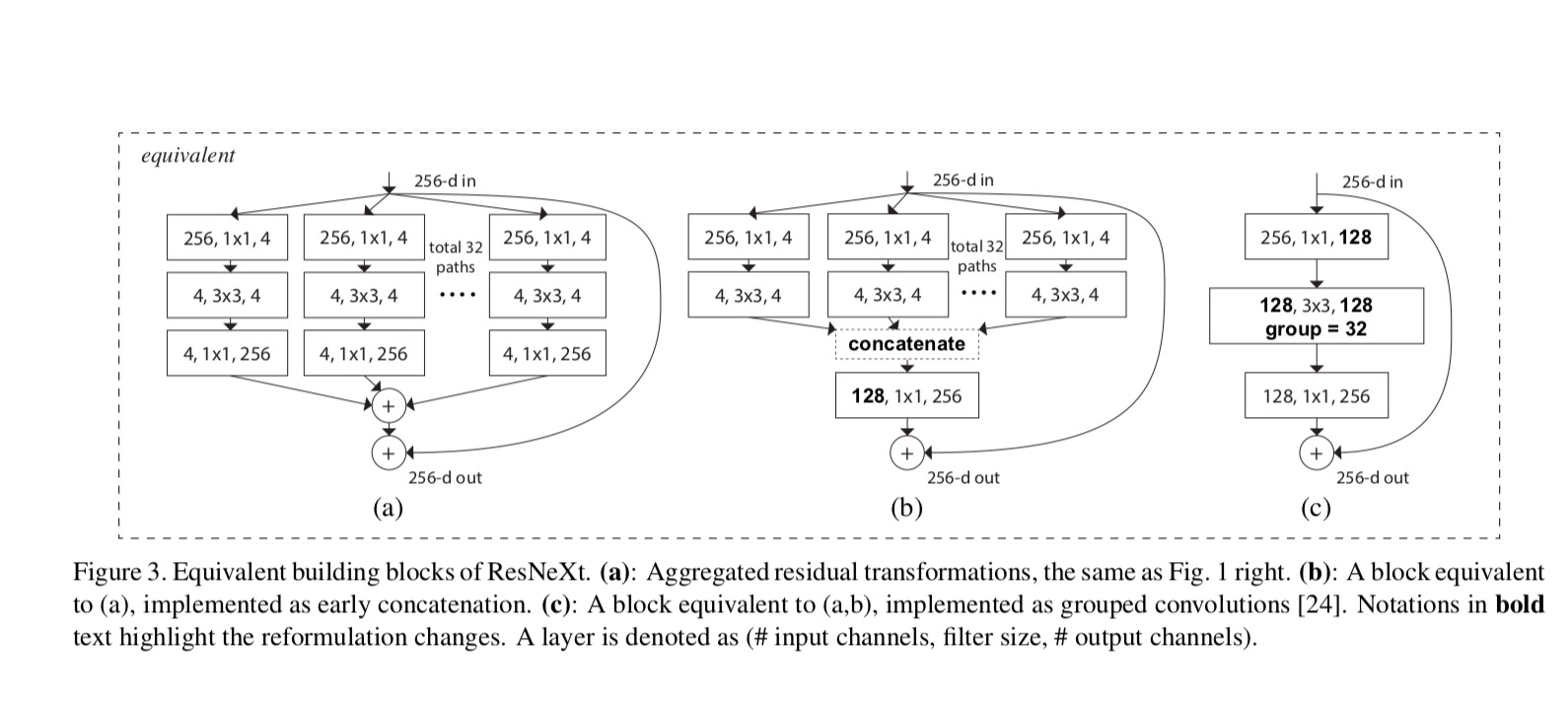
Når vi vurderer forskellige kardinaliteter, mens vi bevarer kompleksiteten, ønsker vi at minimere modifikationen af andre hyper-parametre. Vi vælger at justere bredden af flaskehalsen (f. eks 4-d i Fig 1 (højre)), fordi det kan isoleres fra input og output af blokken. Denne strategi introducerer ingen ændring til andre hyper-parametre (dybde eller input/output bredde af blokke), så er nyttigt for os at fokusere på virkningen af kardinalitet.

i Fig. 1 (Venstre), den oprindelige ResNet flaskehals blok har parametre og proportional FLOPs (på samme funktion kort størrelse). Med flaskehalsbredde , vores skabelon i Fig. 1 (højre) har: parametre og proportionale FLOPs. Hvornår og dette nummer . Følgende tabel viser forholdet mellem kardinalitet og flaskehalsbredde .

eksperimenter

Kardinalitet vs. bredde. Vi vurderer først afvejningen mellem kardinalitet og flaskehalsbredde under bevaret kompleksitet som anført i tabel 2. Tabel 3 viser resultaterne. Sammenlignet med ResNet-50 har 32-4D-50 en valideringsfejl på 22,2%, hvilket er 1,7% lavere end ResNet-baseline ‘ s 23,9%. Da kardinaliteten stiger fra 1 til 32, mens kompleksiteten holdes, reduceres fejlfrekvensen. Desuden har 32-kursen 4d-Næste også en meget lavere træningsfejl end ResNet-tælleparten, hvilket tyder på, at gevinsterne ikke er fra regulering, men fra stærkere repræsentationer.

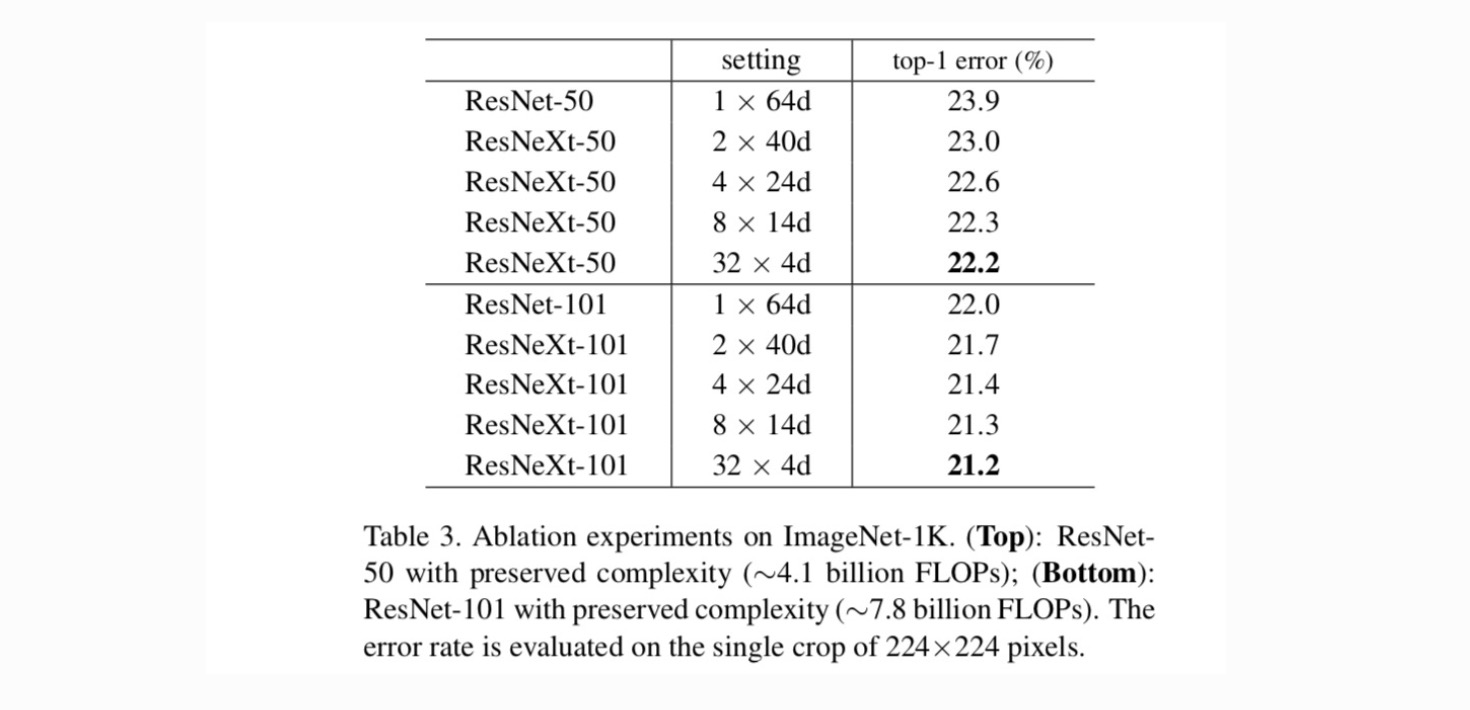
stigende Kardinalitet vs. dybere / bredere.

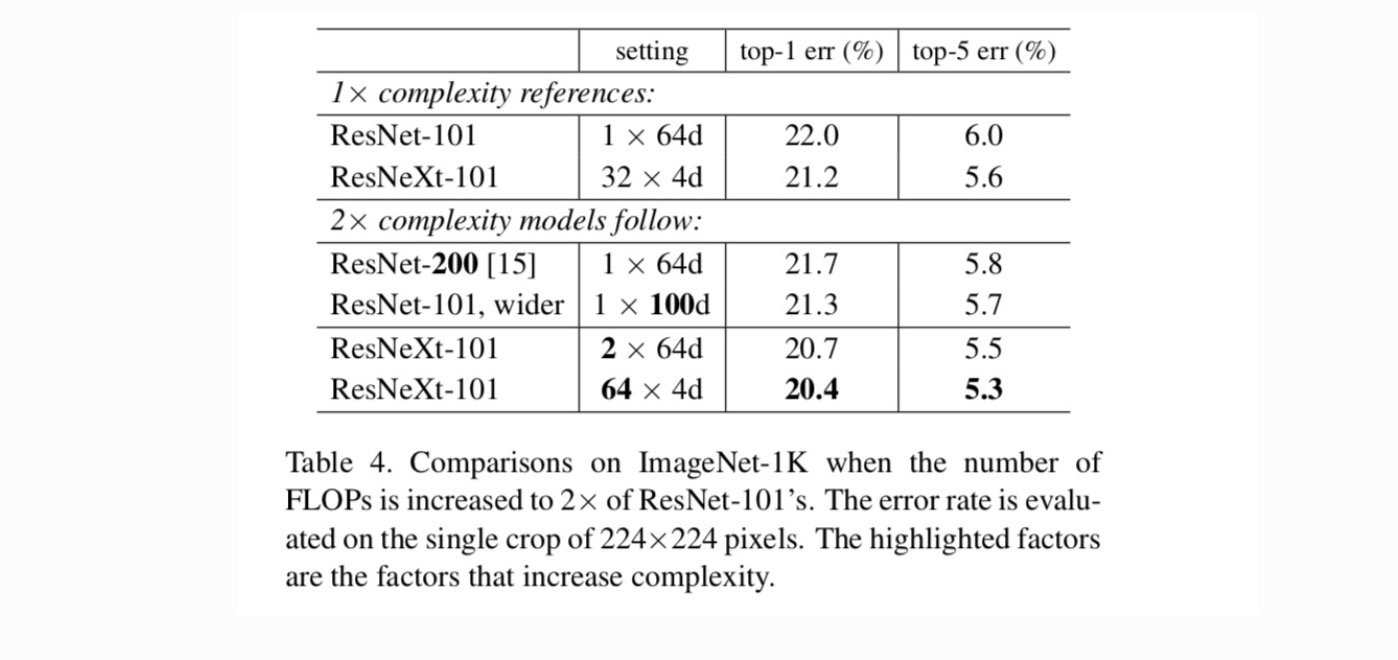
dernæst undersøger vi stigende kompleksitet ved at øge kardinaliteten C eller øge dybden eller bredden. Vi sammenligner følgende varianter (1), der går dybere til 200 lag. Vi vedtager ResNet-200. (2) går bredere ved at øge flaskehalsbredden. (3) forøgelse af kardinaliteten ved fordobling af C.

Tabel 4 viser, at stigende kompleksitet med 2 liter konsekvent reducerer fejl vs. ResNet-101 baseline (22,0%). Men forbedringen er lille, når man går dybere (ResNet-200, med 0,3%) eller bredere (bredere ResNet-101, med 0,7%). Tværtimod viser stigende kardinalitet C meget bedre resultater end at gå dybere eller bredere.

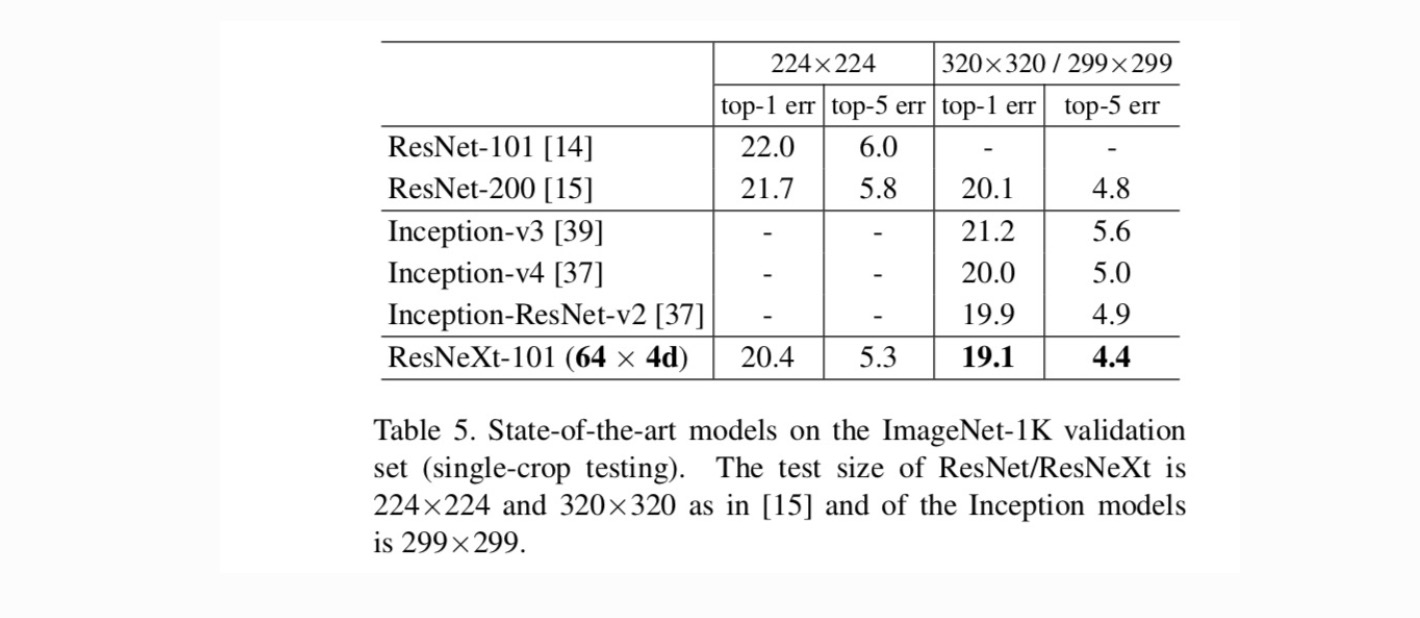
sammenligninger med state-of-the-art resultater. Tabel 5 viser flere resultater af enkeltafgrødetest på ImageNet-valideringssættet. Vores resultater sammenlignes positivt med ResNet, Inception-v3/v4 og Inception-ResNet-v2 og opnår en enkelt afgrøde top-5 fejlrate på 4.4%. Derudover er vores arkitekturdesign meget enklere end alle startmodeller og kræver betydeligt færre hyper-parametre, der skal indstilles manuelt.