Hvad er en dansk model?

Hvad er modellen?

Hvis du har læst vores serie af blog – tutorials om modeller til estimering af tidsseriedata, er du allerede bekendt med 3 store tilgange-autoregression, glidende gennemsnit og integration.

Hvad er det fælles tema i alle disse modeller?

de var udelukkende afhængige af en enkelt variabel.

en model kan dog også tage højde for mere end bare tidligere priser eller tidligere rester.

og disse er de såkaldte “maks” modeller, hvor ARMAKSEN er den ikke-integrerede version og ARIMAKSEN-dens integrerede ækvivalent.

så i denne vejledning skal vi undersøge, hvordan de ser ud og vise dig, hvordan du implementerer dem i Python trin for trin.

lad os komme i gang, skal vi?

Hvorfor hedder ARMAKS “maks” modeller?

navnene kommer som udvidelser af ARMA og ARIMA henholdsvis. I slutningen står “eksogen”. Med andre ord foreslår det at tilføje en separat anden ekstern variabel for at hjælpe med at måle vores endogene variabel.

Modelligningen:

da den eneste forskel mellem ARMAKS og ARIMAKS er, at den ene er integreret, og den anden ikke er, kan vi undersøge en af dem og derefter fremhæve, hvordan den anden ville afvige.

vi udforskede en integreret model i vores sidste blogartikel (ARIMA), så lad os se, hvordan arimaks ligning ser ud.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

selvfølgelig, at ligningen for ARMAX ville være den samme, bortset fra at vi ville bruge den faktiske variable, siger S, i stedet for dens delta.

Pt=c+kr1+kr1 kr1+ kr3

vi kan tænke på ARMAKSEN som et specielt tilfælde af ARIMAKSEN, hvor integrationsrækkefølgen er 0.

så for resten af vejledningen vil vi fokusere på ARIMAKSEN.

og vi begynder med at nedbryde de forskellige dele i den. Til at begynde med repræsenterer Pt og Pt-1 værdierne i henholdsvis den aktuelle periode og 1 periode siden.

på samme måde er krart og krart-1 fejlbetingelserne for de samme to perioder. Og selvfølgelig er c bare en baseline konstant faktor.

de to parametre, lus1 og lus1, udtrykker hvilke dele af værdien Pt-1 og fejl Lust-1 sidste periode er relevante ved estimering af den nuværende.

nu, de to nye tilføjelser til modellen er “H” og dens koefficient. På samme måde som på den anden side er der en koefficient, som vil blive estimeret ud fra modelvalg og data. Men hvad med K?

Hvad er en eksogen variabel?

Nå, det er den eksogene variabel, og det kan være enhver variabel, vi er interesseret i.

det kan være en tidsvarierende måling som inflationen eller prisen på et andet indeks. Eller en kategorisk variabel, der adskiller de forskellige ugedage. Det kan også være en boolsk regnskab for de særlige festlige perioder. Endelig kan det stå for en kombination af flere forskellige eksterne faktorer.

ideen er, at det kan være enhver anden variabel eller variabler, der kan påvirke priserne, så længe vi har de tilgængelige data.

sådanne eksterne faktorer er kendt som eksogene variabler i vores regression. Vi bruger deres værdier til at forudsige og forklare den, vi er interesseret i, hvilket tilfældigvis er aktuelle priser i vores tilfælde.

hvordan implementeres Armaks-og Armaks-modeller i Python?

bekvemt nok kommer statsmodels-pakken ind med en metode kaldet ARIMA, som fuldt ud er i stand til at håndtere sådanne yderligere indgange.

Vi starter med at angive modelens egenskaber og ordrer på modellen:

når vi har gjort det, skal vi også angive det eksogene argument kaldet “eksog”.

den værdi, vi ønsker at passere, skal være en række af en slags, da vi ønsker at have værdier forbundet med hver tidsperiode.

for eksempel kan vi bruge s&p priser som denne eksogene variabel, da vi allerede har dem i vores data.

nu er vi klar til at passe en ARIMAKS (1,1,1) model.

sørg for at navngive din modelvariabel på en måde, der adskiller den fra lignende modeller. I dette tilfælde vælger vi at gøre dette ved at tilføje “i slutningen for at indikere, at den eksogene variabel er S&P.

derefter, som det fremgår af uddragene, sætter vi dette lig med ARIMA-metoden som før, vi tilføjer tidsserien og rækkefølgen, som vi er vant til. Endelig, mellem de to, sætter vi argumentet “eksog” lig med “DF SPC”, som angiver s&p priser.

Hvis vi passer til denne model og udskriver dens oversigtstabel, vil vi se, at vi får en ekstra række til S&p priser.

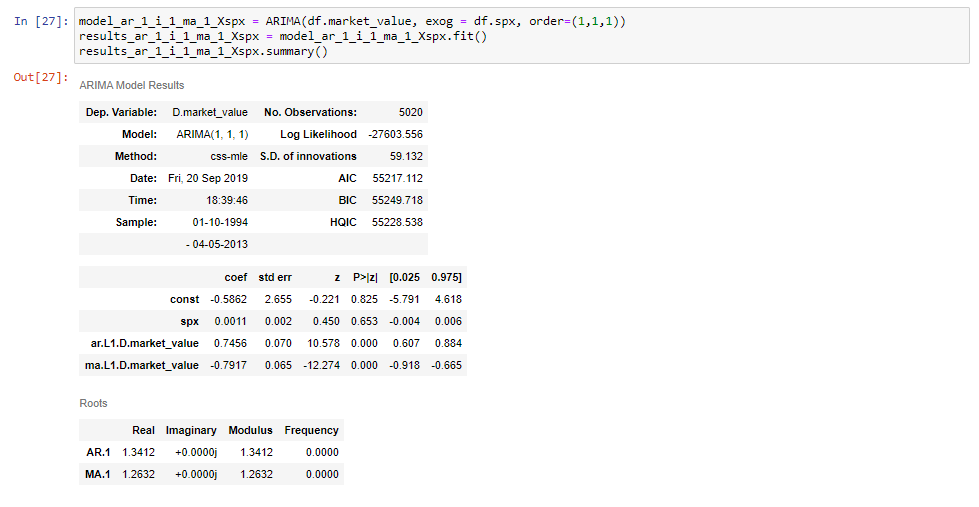
og det er alt der er til det!

vi har med succes set, hvordan man implementerer en Arimaks-model i Python.

Hvis du vil lære mere om Arimak og andre tidsseriemodeller i Python, skal du sørge for at tjekke vores trinvise Python-tutorials. Hvis du er ny til Python, og du er begejstret for at lære mere, vil denne omfattende artikel om læring Python programmering guide dig hele vejen fra installationen, gennem Python IDE ‘ er, Biblioteker og rammer, til de bedste Python karriereveje og Job outlook.

klar til at tage det næste skridt mod en karriere inden for datalogi?

tjek det komplette Datavidenskabsprogram i dag. Start med det grundlæggende med vores statistik, matematik, og udmærke kurser. Opbyg en trinvis oplevelse med Python, R, magt BI og Tableau. Og opgrader dit skillset med maskinlæring, dyb læring, Kreditrisikomodellering, tidsserieanalyse og kundeanalyse i Python. Stadig ikke sikker på, at du vil gøre din interesse for datalogi til en karriere? Du kan udforske læseplanen eller tilmelde dig 15 timers nybegynder til avanceret videoindhold gratis ved at klikke på knappen nedenfor.