ICM Poker: Den eneste Guide, du har brug for

I poker står ICM for “Independent Chip Model”. Det hjælper en pokerspiller på ethvert tidspunkt i en pokerturnering bestemme deres nuværende turnering egenkapital. (Hvor mange penge i præmiepuljen skal i øjeblikket være deres.)

beregningen er baseret på, hvor mange chips de har i øjeblikket i forhold til det samlede antal chips i spil og udbetalingsstrukturen.

disse oplysninger kan bruges til –

• hjælpe spillere i de beslutninger, der skal træffes under en hånd, mens de er i en turnering, især når de er mod de senere eller finalebordsfaser.
• hjælp med at bestemme, hvordan præmiepuljen deles, hvis der er aftalt en “chop” inden afslutningen af en turnering.

Indholdsfortegnelse

ICM-diagram – hvilke faktorer tages i betragtning?

ICM *gør* overveje:	ICM *gør ikke* overvej:
Player’s total size of chip stack	Size of blinds / Stack sizes in blinds
Total # of chips in play	Length of levels
Number of Entrants	Player Skill
Payout structure	Table position
antal resterende spillere	turneringens størrelse

det grundlæggende – hvordan fungerer ICM i poker?

årsagen til at bruge ICM i turneringspoker er, at værdien af hver turneringschip varierer, når hver spiller bliver elimineret og/eller når udbetalingerne fortsætter med at stige. Denne situation er helt ulig i cash games, hvor hvert chipbeløb er fast og repræsentativt for det tilsvarende dollarbeløb.

i et cash game, hvis du fordoble op, du fordoble din egenkapital, fordoble din stak, og fordoble dine penge. I en turnering, du kunne fordoble op på den allerførste hånd, men du stadig ikke har fordoblet din turnering egenkapital.

for at bruge et forenklet eksempel til at hjælpe med at vise dette, lad os antage, at vi har en 10-mand SNG med standardudbetalinger: 1.får 50%, 2. får 30%, og 3. får 20%. Alle spillere får 1.000 turneringschips, hvilket betyder, at der er 10.000 samlede chips i spil.

før turneringen begynder, fortæller ICM os, at (med alle spillere med lige startstakke) har alle spillere den samme EV i turneringen på 10%. (Husk ICM tager ikke dygtighed, bordposition, persienner osv. hensyn. Det tager blot antallet af chips, en spiller har, og relaterer det til det beløb, der er i spil.)

på den allerførste hånd af denne hypotetiske turnering, spiller 1 fordobler op (siddende i big blind) og spiller 10 buster (der sad i small blind). Derfor har Spiller 1 nu 2.000 chips, og alle andre har stadig 1.000 chips.spiller 1 har nu 20% af chips i spil, men har han fordoblet sin turneringskapital fra den oprindelige 10%?

Nej. Hvorfor er dette tilfældet?

på grund af den forskellige struktur i præmiepuljen fordobles fordobling i chips ikke automatisk EV. Havde dette været en vinder-take-all begivenhed, med 20% af chips nu i spil, spiller 1 ville have en 20% skudt på at vinde 100% af præmiepuljen. Derfor ville hans turneringskapital være på 20%.

i denne turnering er præmiepuljen dog også delt mellem 2.og 3. plads. Derfor er det bedste, som enhver spiller kan gøre, at vinde maksimalt 50% samlet egenkapital i turneringen-50% af den samlede præmiepulje. De har også en chance for at tage hjem måske 30% eller 20% af turneringens egenkapital, hvis de placerer i 2.eller 3. Det er for disse ekstra placeringer, at ICM bruges til at beregne en mere nøjagtig gengivelse af ens turneringsværdi.

ved at bruge en ICM-regnemaskine kan vi se, at Player 1s turneringskapital nu er på 18.44%. Derfor, mens fordobling af hans stak øgede sin egenkapital betydeligt i turneringen fra 10% til 18.44%, fordoblede han ikke fuldt ud denne egenkapital.

hvorfor er dette, og hvor gik den resterende egenkapital hen?

de andre otte resterende spillere modtog den ekstra turneringskapital og fik 0,19% egenkapital fra spiller 10 busting. Og de spillede ikke engang en hånd! Denne stigning i egenkapitalen giver mening, da der nu er en spiller mindre at konkurrere mod med samme mængde chips i spil.

Bemærk: Udbetalingen beløb, der anvendes for hvert sted ITM vil også påvirke ICM og beregning turnering aktier. Havde det været en 1.-2.-3. opsætning med udbetalinger på 65% -25% -10% af den samlede præmiepulje, ville spiller 1 ‘ s egenkapital have sprunget til præcist 19% ved at gentage det samme scenario!

flere ICM BASICS: Beregning af ICM (Simple)

for yderligere at illustrere, hvorfor fordobling af ens chipstak ikke fordobler ens turneringsværdi (og også for yderligere at forstå begrebet ICM i turneringspoker) overvej dette:

to spillere forbliver i en 6-mands SNG, hvor hver spiller startede med 1.000 chips. Udbetalingerne er 70% for 1. og 30% for 2. Spiller 1 har en massiv chip lead med 5.900 chips. Spiller 2 har en sølle stak af 100 chips. Efter den ene hånd formår spiller 2 at fordoble sine chips, hvilket betyder, at stakstørrelserne nu er 5.800 og 200.

fordoblede spiller 2 ‘ s turnering egenkapital ved at fordoble sin stak?

nej, nej, det har ikke.

med kun to spillere tilbage, er hver spiller garanteret 30% af præmiepuljen. Denne procentdel repræsenterer det værste resultat hver spiller kunne gå væk med, hvis de taber turneringen.

derfor vil spillere med eventuelle chips tilbage have et sted over 30% egenkapital i turneringen. Som sådan ville de to resterende spillere i dette eksempel konkurrere om de resterende 40% af præmiepuljen. (Ja, det samlede beløb for 1. er 70% af præmiepuljen, men fordi hver spiller har mindst 30% låst op, efterlader dette den resterende turneringskapital på højkant. Og forskellen mellem 1. (70%) og 2. plads (30%) er 40%.)

så længe Spiller 2 stadig har chips, er der en lille chance for, at han kunne komme tilbage og vinde. H har en lille del af egenkapitalen i den resterende 40%.

derfor, med kun 100 chips, spiller 2 ville have turnering egenkapital på 30.67%. Vi ankommer til dette tal ved at tage den basiskapital, han allerede er sikret (30%), og tilføje det til hans sandsynlighed (baseret simpelthen på antallet af chips i hans stak i forhold til det samlede antal i spil) for at vinde den resterende 40% egenkapital:

= 30% garanteret egenkapital + ((100 chips/6.000 samlede chips) * 40% resterende turnering)

= 0.3 + (0.0167 * 0.4)
= 0.3 + 0.0067
= 0.3067

Sådan beregnes ICM i Poker

som du kan se, fordobler en stak i en pokerturnering ikke ens egenkapital. Det er vigtigt at vide, hvordan man beregner ICM, så du kan træffe de tilsvarende beslutninger strategisk, fra hånd til hånd. (Se senere afsnit i denne artikel.)

også, så du ved, hvor meget hver spiller skal få, hvis en “chop” – situation nogensinde opstod ved finalebordet. Imidlertid, i modsætning til i det foregående afsnit med spillere heads-up, beregninger vil få en lille smule mere kompliceret med flere spillere tilføjet i blandingen.

den måde, vi beregner ICM manuelt i et scenarie med flere (3+) spillere tilbage i en turnering, er som følger. Vi tager antallet af chips en spiller har (i forhold til det samlede antal chips i spil) og bruger dette til at beregne sandsynligheden for, at spilleren placerer sig på hvert resterende sted i en turnering.

efter dette vil vi relatere disse procentsatser til de tilsvarende pengepræmier, der er knyttet til hvert sted, og derefter tilføje resultaterne af alle resultaterne sammen.

lad os bruge en virkelig situation med spillerne og deres chiptællinger taget fra starten af Dag 9 (3-hånds spil) under 2019-hovedbegivenheden i Las Vegas:

• Hossein Ensan – 326.800.000 (63,5% chips i spil)
• Dario Sammartino – 67.600.000 (13,1% chips i spil)

Livingston – 120.400.000 (23,4% chips i spil)

samlede chips i spil: 514.800.000

bemærk: Mens en chop aldrig fandt sted i denne turnering, følgende beregninger vises for at illustrere, hvordan man laver manuelle ICM-beregninger for en multiplayer-chop.

med tre spillere tilbage var der seks muligheder for, hvordan turneringen kunne have afsluttet.

disse muligheder vil blive opført her i rækkefølge af 1., 2. og 3. plads:

1) Ensan, Sammartino, Livingston
2) Ensan, Livingston, Sammartino
3) Livingston, Ensan, Sammartino
4) Sammartino, Ensan, Livingston
5) Livingston, Sammartino, Ensan
6) Sammartino, Livingston, Ensan

for vores ICM-beregninger, lad os antage, at vi prøver at finde ICM-turneringens egenkapital for Hossein ensan, dagen 9 Chip leder. Du vil bemærke, at-i ovenstående tabel-Ensan havde to muligheder for at placere 1., to for at placere 2. og to chancer for at placere 3..

for at hjælpe os med at konvertere det hele til ICM-turneringens egenkapital skal vi bestemme sandsynligheden for, at han afslutter turneringen hvert sted (baseret på aktuelle chipstakstørrelser).

Sandsynlighed for at placere 1. — Options 1 + 2

Med Ensan med 63,5% af chips i spil, er der en 63,5% chance for, at han får 1., baseret udelukkende på at tage sit nuværende antal chips i forhold til det samlede beløb i spillet.

Sandsynlighed for at placere 2. — indstillinger 3 + 4

for dette afsnit bliver vi nødt til at beregne indstillingerne separat for at tage højde for de to andre spillers sandsynligheder for at placere 1.foran ham.

for option 3 har Livingston en 23,4% chance for at komme ind 1. For at bestemme sandsynligheden for, at Ensan derefter kommer 2. (mellem ham og Sammartino), skal vi tage (Ensans chips/resterende spilleres chips-i dette tilfælde Ensans + Sammartino’ s).

denne formel giver os svaret på (326,800,000 / (326,800,000 + 67,600,000) = 82.9%, det betyder, at der er en 82.9% chance for Esan kommer 2nd, hvis Livingston placerer 1st.

for at bestemme den samlede sandsynlighed for denne mulighed, skal vi nu multiplicere disse to muligheder sammen (Livingston vindende og Ensan kommer i 2nd): 0.234 * 0.829 = 0.194 = 19.4% chance dette scenario vil forekomme.

For mulighed 4 i tabellen gør vi de samme beregninger, men med Sammartino kommer 1st (13.1% chance). Ved hjælp af den samme matematiske formel (13,1% (328,8 millioner / 447,2 millioner) finder vi, at dette resultat har en 9,6% chance for at forekomme, baseret på ICM og chip stakke.

tilføjelse af sandsynligheden for hvert scenarie (19,4% og 9,6%) ser vi, at der er en 29% chance for, at Ensan kommer på 2.pladsen.

Sandsynlighed for at placere 3. — optioner 5 + 6

den resulterende Sandsynlighed for Ensan kommer 3.ville være 7,5%. Vi ankommer til dette nummer ved at opdage, at der er en 4% af Option 5, der forekommer (23,4% * (67,6 millioner / 394,4 millioner)) og en 3,5% chance for, at Option 6 forekommer (13,1% * (120,4 millioner / 447,2 millioner)).

konvertering af % til $ ved hjælp af ICM

Ved hjælp af disse procenter kan vi derefter beregne den EV, som en spiller i øjeblikket har i $$$ i en turnering, hvilket netop er det, der ville blive brugt til at beregne udbetalinger, hvis der opstod en situation at “hugge”.

så fortsætter vi med vores eksempel, her er hvad de 3 bedste præmieudbetalinger var for 2019 Main Event:

• 1st – $10.000.000
• 2nd – $6.000.000
• 3rd – $4.000.000

Her er $EV Ensan har til efterbehandling i hver sted:

• EV af 1. = 0,635 * $10.000.000 = $6.350.000
• EV af 2. = 0,290 * $6.000.000 = $1.740.000
• EV af 3. = 0,075 * $4.000.000 = $300.000

det sidste trin: beregning af ens egenkapital med flere spillere tilbage

ICM-formel til ICM-beregning

for at opsummere det foregående afsnit om ICM-beregning er her den trinvise formel, der skal bruges til at beregne din turneringskapital baseret på ICM-overvejelser:

1. Bestem størrelsen i chips for hver spillers chipstack

1. relatere dette til det samlede antal chips i spil –

• Chipstack/Total Chip
• denne beregning viser hver spillers Sandsynlighed for at vinde turneringen.

1. Bestem sandsynligheden for alle de forskellige muligheder for, hvordan turneringen ender (med hensyn til hvilket sted hver spiller kan få)-

• Bestem alle de forskellige mulige resultater.
• Bestem sandsynligheden for hvert resultat ved at starte med sandsynligheden for, at vinderen af hvert scenarie får 1.pladsen.
• efter dette, for at bestemme 2. plads Sandsynlighed, flere vinders muligheder for at vinde (deres chip share) ved (2.plads chips/total resterende andre chips, herunder 2. plads).
• for at gøre denne formel for mere end tre spillere skal du kombinere sandsynligheden for 1.og 2. plads (osv.) før beregning for en spiller i en senere position.

1. relaterer disse aktier til det $ beløb, der er knyttet til de betalte steder for at bestemme EV-

ICM-program til ICM-beregninger

som vist i eksemplet ovenfor, selv med kun tre spillere tilbage i en turnering, er mængden af ICM-beregninger, der skal gøres for at beregne EV, allerede ret lang. (Og på det beregnede vi EV / ICM for kun en spiller af de tre pågældende!)

Forestil dig at lave disse beregninger, hvis spillet var 4-håndet eller 5-håndet, eller lige efter at spillerne kom ind i pengene! Antallet af kombinationer for, hvordan hver spiller ville ende med at blive utrolig tidskrævende, hvis det gøres manuelt.

derfor er det på grund af længden og kompleksiteten af disse beregninger ikke ualmindeligt, at spillere / pokerrum bruger ICM – programmer og ICM-regnemaskiner-især hvis spillerne ønsker at hugge.

ICM Gameplay overvejelser: Stack størrelser og ICM pres

kommer på ICM fra en mere strategisk / gameplay perspektiv nu, ICM pres kan komme i mange former og forskellige situationer. Primært henviser dette udtryk til de begrænsninger og ændringer, som en spiller skal foretage i deres håndområder og/eller hvordan de spiller specifikke hænder. Spillere ønsker ikke at miste store mængder egenkapital i en turnering, hvis de overhovedet kan undgå det på grund af ICM og udbetalingsimplikationer.

som et typisk eksempel, se på en fælles situation, der kommer op, når ITM (i pengene) i SNG ‘ s. normalt er der altid en spiller med hver af følgende stakke: 1 stor stak, 1 medium stak og 1 kort stak.

lad os antage, at spillerne har stakstørrelser på 3.000, 6.000 og 9.000 chips.

hvordan disse forskellige stakstørrelser efterfølgende skal relateres og justeres på grund af ICM-tryk og overvejelser er ret ligetil:

1. som medium stack ønsker du ikke at komme ind i episke konfrontationer med big stack, fordi dette kan koste dig egenkapital og/eller dit turneringsliv. Du foretrækker at se short stack buste ud først (efterfølgende stigende i din turnerings egenkapital), før du bliver for stærkt involveret i en stor pot med big stack. Samtidig kan mediestakken tage * nogle * chancer mod den korte stak, selvom den stadig skal udvise forsigtighed. Mens han ikke vil buste og miste al sin egenkapital i turneringen, hvis han tabte en all-in til short stack, ville det sandsynligvis forlade ham på rebene og blive short stack.

1. af ovenstående grund kan du som den store stak anvende et stort pres på både mellemstakken og den korte stak, men især mellemstakken. Han er i håndjern mellem dig og den korte stak. Han vil hellere bevare sin turnering egenkapital og potentielt få nogle, hvis du er i stand til at buste den kortere stak. Og mens short stack * kunne * sætte en lille bule i din stack, selv efter at de fordobles gennem dig, vil du stadig have betydelig egenkapital i turneringen.

ICM Gameplay overvejelser: Boblen

disse” relative stack størrelse “begreber gælder ikke kun, når der er tre personer tilbage; de kan også gælde for hele finalebordet i en MTT (da der normalt er et lønspring for hver eliminering), såvel som når” pengeboblen ” er ved at briste.

boblen er en unik del af en pokerturnering. Afslut ud af pengene, og du har mistet alle turnering egenkapital (og har intet at vise for det). Cruise forbi boblen og ikke kun får du at fortsætte med at spille, men du har også et minimum af turnering egenkapital låst op, som efterfølgende vil have en dejlig, rentabel payday at gå sammen med det!

ICM overvejelser er meget udbredt under boblen i en pokerturnering. Som sådan søger korte stakke i løbet af denne tid normalt at undgå enhver konfrontation og ikke gå i stykker.

ICM katastrofe: En hånd eksempel

en intens hånd fra verden serie af Poker 2010: Main Event Final Table viser fremtrædende ICM overvejelser er, og hvor massiv en skade for ens turneringsresultater, de kan være.

for at sætte scenen, med tre spillere tilbage, var her chiptællingerne, før katastrofen i en hånd begyndte:

• John Racener – 36.450.000 (17% af chips tilbage)
• Jonathan Duhamel – 88.100.000 (40% af chips tilbage)
• Joseph Cheong – 95.050.000 (43% af chips tilbage)

John Racener foldede knappen. Joseph Cheong rejste til 2,9 millioner fra small blind med As7h. Duhamel 3bet til 6,75 millioner med Small blind. Cheong 4bet til 14.25 million. Duhamel 5bet til 22,75 millioner.

og derefter… Cheong 6-bet rippet det for 95,05 millioner, have Duhamel dækket!

før vi kommer til resultaterne af hånden, lad os kort dykke ned i at analysere Cheongs beslutning om at 6bet jam A7o:

• Cheong har et ess i hånden, hvilket hjælper med at reducere antallet af esser, som Duhamel kunne have. (De mulige kombinationer af AK eller AK reducerer fra 16 til 12. Det halverer også antallet af Pocket Aces combos, som Duhamel kunne have fra 6 til 3.)
• Cheong har en lille chipledning over Duhamel, hvilket utvivlsomt er signifikant. Mens begge spillere har omtrent samme turneringskapital i øjeblikket, hvis begge spillere går all-in og Duhamel taber, så er det en temmelig stor aftale. Primært på grund af den nuværende størrelse af Raceners stak i sammenligning med dem begge, såvel som den efterfølgende egenkapital, han ville miste til Racener ved at sprænge.

kort sagt, Cheong satte Duhamel i et fascinerende, meget trykfyldt sted. Ja, Mens der sandsynligvis er et bedre udvalg af ØKSEHÆNDER, som Cheong i sidste ende kunne have besluttet at 6bet bluff skubbe med (enten egnede eller hjul/tilsluttede kombinationer), sætter det utvivlsomt Duhamel på prøve, især når du faktor ICM overvejelser i det (at Duhamel kunne buste bag Racener, hvis han kalder all-in og taber).

når det er sagt, skubber 6bet på lang sigt A7o på dette sted a +EV-spil? Sikkert ikke. (Vi bliver nødt til at dissekere håndområder, håndaktier og turneringsaktier rigeligt for at gøre dette.) Men når man tænker på lang sigt, kan dette spil have kostet Cheong millioner af dollars i egenkapital.

ICM Gameplay overvejelser: strategi og teori

i cash games, hvis du står over for en all-in stedet, for at vise langsigtet profit, bør du:

• Beregn dine pot odds og den egenkapital, du har brug for for at vinde hånden for at foretage et rentabelt opkald.
• Bestem din hånds faktisk egenkapital mod en omtrentlig rækkevidde af din modstander.
• foretag opkaldet, hvis du har de relevante odds (+chipEV-opkald) eller fold, hvis du ikke har tilstrækkelige odds/egenkapital til det pågældende sted.

for turneringssituationer er det dog ikke altid så skåret og tørt på grund af (du gættede det!) ICM overvejelser.

som et eksempel, lad os sige, at vi er på boblen af en 9-hånds SNG (4 spillere forbliver). Alle har lige stakke af 4.500. Blinds er 200/400, og der er en 25 ante, så godt. CO folder, BTN går all-in, SB folder, og vi ser ned på KJ ‘ er i BB.

1. er dette et opkald baseret på ICM (næste spiller til busts blade med ingenting, alle andre gør pengene)?
2. hvor meget egenkapital er vundet / tabt ved at ringe her?

for det første må vi antage, at knappen skubber rækkevidde, som meget vel kunne se sådan ud (42,87% af hænderne):

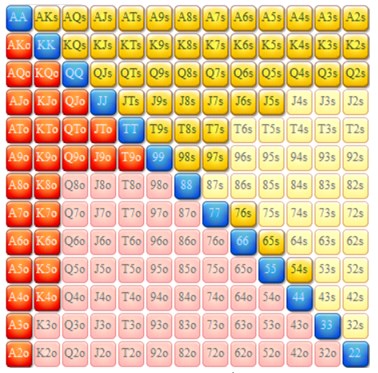
22+,A2+,K2s+,K4o+,2s+,9o+,J5s+,J9o+,T7s+,T9o,97s+,76s,65s,54s

mod dette interval kan vi bruge en egenkapitalberegner til at bestemme, at 47,69% egenkapital for at vinde hånden, 3,10% for at binde og 49,21% egenkapital for at miste hånden i forhold til dette interval. Med vores big blind og ante allerede i midten, ville vi nødt til at aflyse 4,075 chips mere for at vinde de 5,175 chips i midten (small blind + big blind + antes + villain ‘ s shove).

i et cash game ville vi simpelthen bestemme, via pot odds, at vi ville have brug for 44,05% egenkapital for at ringe. Mod den formodede knap, der skubber rækkevidde af vores modstander, synes vores samlede egenkapital (herunder tie muligheder) på 49.24% at gøre det godt, hvilket betyder, at vi skal ringe…hvis dette var et cash game!

fordi dette er en turnering (med efterfølgende ICM implikationer), er svaret ikke så simpelt.

for at afgøre, om vi skal ringe eller folde dette sted i en turnering, skal vi finde ud af turneringen EV for hver mulighed! For at gøre dette skal vi tage sandsynligheden for hvert resultat (vinde, binde, tabe), multiplicere disse med den chip EV, som hvert resultat ville bringe (baseret på nye chipstakke efter hånden).

og derefter tilføje dem sammen for at nå frem til den samlede nye turnering EV for at foretage et opkald:

% Chance for sejr/tab/uafgjort turnering EV (% af præmiepuljen) efter hånden

Vind: 47,69% 38,72%

uafgjort: 3,10% 25,45% (hugge SB/antes af andre spillere)

tabe: 49,21% 0% p ved at tilføje alle disse resultater sammen, kan vi se, at vores turnering EV, baseret på ICM, hvis vi kaldte her ville være 18.47% + 0.79% + 0% = ~19.25%.

nu skal vi sammenligne dette med vores turneringskapital, hvis vi foldede. Efter hånden ville nye stakstørrelser være som følger (på grund af tab af blinds/antes):

• BB (Hero): 4075
• SB: 4,275
• BTN (skurk):, 5175,
• CO: 4,475

Ved at tilslutte disse stakstørrelser til en ICM-lommeregner kan vi se, at vores nye turneringsværdi (som et resultat af foldning) ville være 23,47%. Ved at ringe til JJS her, mister vi en forbløffende (23.47% – 19.25%) = 4.22% af vores turnering egenkapital (i gennemsnit) ved at ringe her, hvilket er ganske betydelig!

som et resultat kan vi se, hvordan det i et cash game baseret på pot odds og den samme situation ville være et let opkald. Imidlertid, med ICM-implikationer i en 9-mands SNG på boblen, denne KJ ‘ er bliver pludselig et let “kast i mucken.”

Bemærk: Bemærk, hvordan et marginalt dårligt opkald (som illustreret her i dette SNG-eksempel) kan forårsage 4.22% tab af turneringens egenkapital? Forestil dig nu en lignende situation med fire spillere tilbage ved finalebordet ved Main Event! Med omkring $23 millioner på højkant i de sidste fire pletter (baseret på 2019 udbetaling struktur), 4.22% egenkapital svarer til et kæmpe $970,600 tab i monetær egenkapital!

ICM-program til ICM-praksis: Push / Fold-spillet

udbetalingsstrukturen i en turnering (ud over at relatere ens nuværende stackstørrelse til alle andres) hjælper bestemt med at bestemme, hvad der vil være den mest rentable måde at spille på.mens ovenstående eksempler viser toppen af isbjerget til manuelle beregninger, er den gode nyhed, at programmer kan hjælpe. Flere programmer er udviklet til at hjælpe spillere med at forbedre deres push/fold spil og overordnede gameplay for ICM pletter som ovenstående.

Mobile apps som SnapShove kan hjælpe dig med at give dig et udgangspunkt for at forbedre dit All-in-or-fold spil. Med tilpassede funktioner som antal spillere, bordposition, effektive stakke, antes og persienner, vil dette uden tvivl hjælpe dig med at få bolden til at rulle i den rigtige retning.

for at tage dit spil et skridt videre, og også at indarbejde sådanne push/fold beregninger specifikt med ICM og udbetaling overvejelser, Icmisator (https://www.icmpoker.com/icmizer/) er en cool værktøj til at undersøge, der vil hjælpe dig med at gøre netop det. (Tilgængelig via computer og til hentning af vinduer.) Det vil også hjælpe med at forenkle mere komplicerede beregninger, der ville være meget tidskrævende, hvis du skulle gøre dem for hånd hver gang.

Når vi ser tilbage på vores sidste eksempel, kunne vi nemt have brugt Icmiser til at vise os resultaterne på et øjeblik!

ICM Resume

forhåbentlig har denne omfattende guide med succes vist dig, hvordan du lærer ICM poker, og hvordan du også studerer det. Mens du bruger ICM, er det bestemt ikke en perfekt løsning (dvs.da det ikke tager dygtighed, spillerpositioner, hvem der sender deres big blind næste osv. i betragtning) tillader det spillere at have en baseline forståelse af deres nuværende turneringskapital.

Ved at studere med det program, der anbefales ovenfor (og måske ved at prøve et par ICM-eksempler), vil det at kende den uafhængige Chipmodel i sidste ende forbedre dit gameplay.

det vil også give dig mulighed for at gøre mere +EV beslutninger, og efterfølgende hjælpe dig med at tjene flere penge på felts i pokerturneringer.