Introduktion til Bevægelsesestimering med optisk strøm

i denne tutorial dykker vi ned i fundamentet for optisk strømning, ser på nogle af dens applikationer og implementerer dens to hovedvarianter (sparsom og tæt). Vi diskuterer også kort nyere tilgange ved hjælp af dyb læring og lovende fremtidige retninger.

nylige gennembrud inden for computersynsforskning har gjort det muligt for maskiner at opfatte sin omgivende verden gennem teknikker såsom objektdetektion til detektering af forekomster af objekter, der tilhører en bestemt klasse og semantisk segmentering til billedvis klassificering.

til behandling af videoinput i realtid adresserer de fleste implementeringer af disse teknikker kun forhold mellem objekter inden for den samme ramme \((h, y)\) bortset fra tidsinformation \((t)\). Med andre ord revurderer de hver ramme uafhængigt, som om de er helt uafhængige billeder, for hvert løb. Men hvad hvis vi har brug for forholdet mellem på hinanden følgende rammer, for eksempel vil vi spore bevægelsen af køretøjer på tværs af rammer for at estimere dens nuværende hastighed og forudsige dens position i den næste ramme?

eller alternativt, hvad hvis vi har brug for information om menneskelige positionsrelationer mellem på hinanden følgende rammer for at genkende menneskelige handlinger som Bueskydning, baseball og basketball?

i denne tutorial lærer vi, hvad optisk strøm er, hvordan man implementerer dens to hovedvarianter (sparsom og tæt), og får også et stort billede af nyere tilgange, der involverer dyb læring og lovende fremtidige retninger.

Hvad er optisk strømning?
implementering af sparsom optisk strøm
implementering af tæt optisk strøm
dyb læring og videre

Hvad er optisk strøm?

lad os begynde med en forståelse på højt niveau af optisk strømning. Optisk strømning er bevægelse af objekter mellem på hinanden følgende sekvensrammer forårsaget af den relative bevægelse mellem objektet og kameraet. Problemet med optisk strømning kan udtrykkes som:

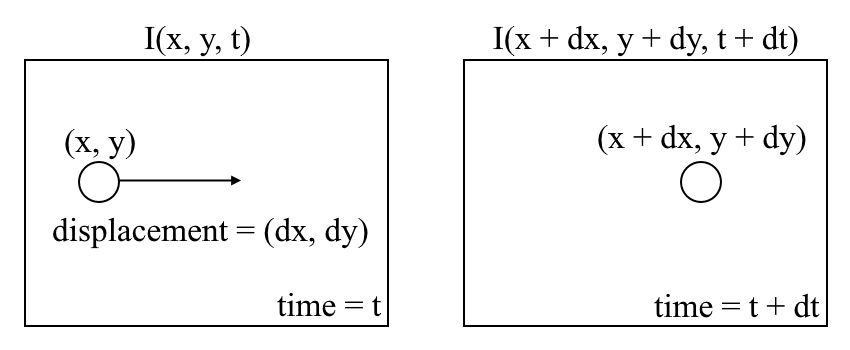
hvor mellem på hinanden følgende rammer kan vi udtrykke billedintensiteten \((I)\) som en funktion af rummet \((H, y)\) og tid \((t)\). Med andre ord, hvis vi tager det første billede \(i(H, y, t)\) og flytter dets billedpunkter med \((DH, dy)\) over \(t\) tid, får vi det nye billede \(I(h + DH, y + dy, t + dt)\).

for det første antager vi, at billedintensiteter af et objekt er konstante mellem på hinanden følgende rammer.

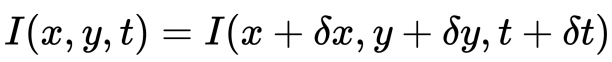
for det andet tager vi Taylor-serien tilnærmelse af RHS og fjerner almindelige udtryk.

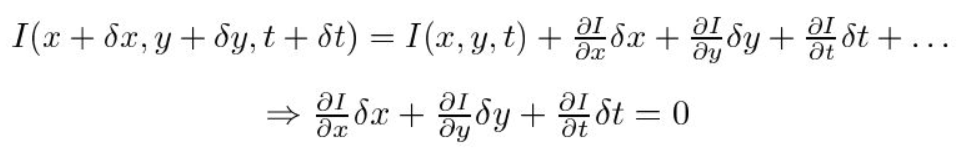
for det tredje deler vi med \(dt\) for at udlede den optiske strømningsligning:

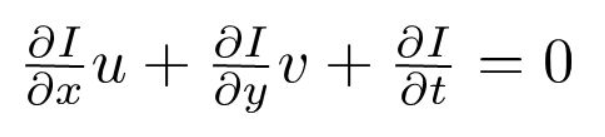
hvor \(u = DH/dt\) og \(v = dy/dt\).

\(dI/ dy, di / dy\) og \(dI/dt\) er billedgradienterne langs den vandrette akse, den lodrette akse og tiden. Derfor konkluderer vi med problemet med optisk strømning, det vil sige at løse \(u (DH/dt)\) og \(v (dy/dt)\) for at bestemme bevægelse over tid. Du bemærker muligvis, at vi ikke direkte kan løse den optiske strømningsligning for \(u\) og \(v\), da der kun er en ligning for to ukendte variabler. Vi vil implementere nogle metoder såsom Lucas-Kanade-metoden til at løse dette problem.

sparsom vs tæt optisk strøm

sparsom optisk strøm giver strømningsvektorerne af nogle “interessante funktioner” (siger få billedpunkter, der viser kanterne eller hjørnerne af et objekt) inden i rammen, mens tæt optisk strømning, som giver strømningsvektorerne for hele rammen (alle billedpunkter) – op til en strømningsvektor pr. Som du ville have gættet, har tæt optisk strømning højere nøjagtighed på bekostning af at være langsom/beregningsmæssigt dyr.

implementering af sparsom optisk strøm

sparsom optisk strøm vælger et sparsomt funktionssæt med billedpunkter (f.eks. interessante funktioner såsom kanter og hjørner) til at spore dens hastighedsvektorer (bevægelse). De ekstraherede funktioner passeres i den optiske strømningsfunktion fra ramme til ramme for at sikre, at de samme punkter spores. Der er forskellige implementeringer af sparsom optisk strømning, herunder Lucas–Kanade–metoden, Horn-Schunck-metoden, Bukstonmetoden og mere. Vi bruger Lucas – Kanade-metoden med OpenCV, et open source-bibliotek med computervisionalgoritmer, til implementering.

opsætning af dit miljø

Hvis du ikke allerede har OpenCV installeret, skal du åbne Terminal og køre:

pip install opencv-python

nu klone tutorial repository ved at køre:

git clone https://github.com/chuanenlin/optical-flow.git

næste, åbn sparse-starter.py med din teksteditor. Vi skriver al koden i denne Python-fil.

konfiguration af OpenCV til at læse en video og opsætning af parametre

Shi-Tomasi Hjørnedetektor – valg af billedpunkter til at spore

til implementering af sparsom optisk strømning sporer vi kun bevægelsen af et funktionssæt med billedpunkter. Funktioner i billeder er interessepunkter, der præsenterer rig billedindholdsinformation. For eksempel kan sådanne funktioner være punkter i billedet, der er uforanderlige for ændringer i oversættelse, skala, rotation og intensitet, såsom hjørner.

shi-Tomasi-Hjørnedetektoren ligner meget den populære Harris-Hjørnedetektor, som kan implementeres ved hjælp af følgende tre procedurer:

1. Bestem vinduer (små billedpatcher) med store gradienter (variationer i billedintensitet), når de oversættes i både \(h\) og \(y\) retninger.
2. for hvert vindue skal du beregne en score \(R\).
3. afhængigt af værdien af \(R\) klassificeres hvert vindue som en flad, kant eller hjørne.

Hvis du gerne vil vide mere om en trinvis matematisk forklaring af Harris Corner Detector, er du velkommen til at gå gennem disse dias.

Shi og Tomasi lavede senere en lille, men effektiv ændring af Harris Corner Detector i deres papir gode funktioner til at spore.

modifikationen er til ligningen, hvor score \(R\) beregnes. I Harris Hjørnedetektoren er scoringsfunktionen givet af:

$$
\begin{array}{c}{R=\operatorname{det} m-k(\operatorname{trace} M)^{2}}\ny linje \
{\operatorname{det} m=\lambda_{1} \lambda_{2}}\ny linje \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\end{array}
$$

i stedet foreslog shi-Tomasi scoringsfunktionen som:

$$
r=\min \Left(\lambda_{1}, \lambda_{2}\right)
$$

hvilket grundlæggende betyder, at hvis \(r\) er større end en tærskel, klassificeres den som et hjørne. I det følgende sammenlignes scoringsfunktionerne for Harris (venstre) og Shi-Tomasi(højre) i \(LR1-lrr2\) plads.

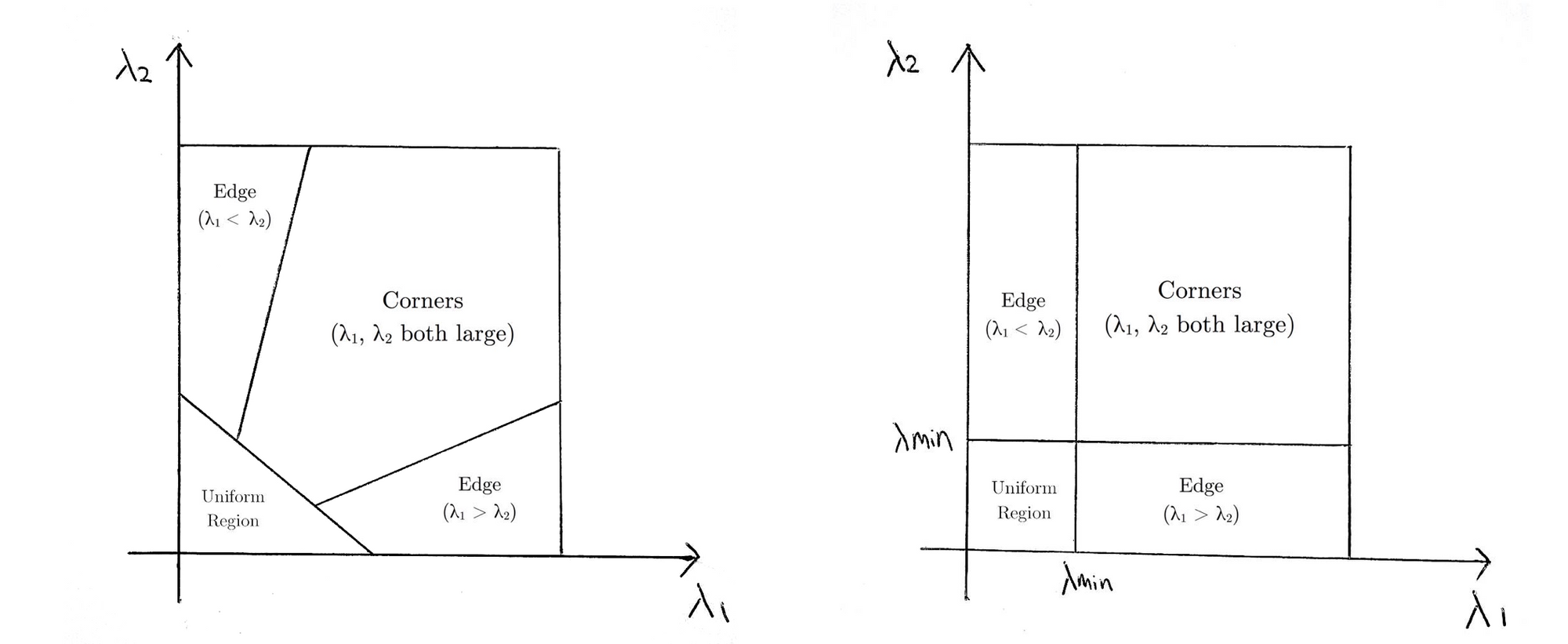
for Shi-Tomasi er vinduet kun klassificeret som et hjørne, når \(larr1\) og \(larr2\) er over en minimumstærskel \(larrmin\).

dokumentationen af Opencvs implementering af Shi-Tomasi via goodFeaturesToTrack() kan findes her.

sporing af specifikke objekter

der kan være scenarier, hvor du kun vil spore et bestemt objekt af interesse (f.eks. Du kan nemt ændre koden for at spore billedpunkterne for det eller de objekter, du ønsker, ved at ændre prev variablen.

Du kan også kombinere objektdetektering med denne metode til kun at estimere strømmen af billedpunkter inden for de detekterede afgrænsningsbokse. På denne måde kan du spore alle objekter af en bestemt type/kategori i videoen.

Lucas-Kanade: sparsom optisk strøm

Lucas og Kanade foreslog en effektiv teknik til at estimere bevægelsen af interessante funktioner ved at sammenligne to på hinanden følgende rammer i deres papir en iterativ Billedregistreringsteknik med en applikation til Stereo Vision. Lucas-Kanade-metoden fungerer under følgende antagelser:

1. to på hinanden følgende rammer adskilles med en lille tidsforøgelse (\(dt\)), således at objekter ikke forskydes signifikant (med andre ord fungerer metoden bedst med langsomt bevægelige objekter).
2. en ramme skildrer en “naturlig” scene med teksturerede objekter, der udviser gråtoner, der ændrer sig glat.

for det første kan vi under disse antagelser tage et lille 3H3-vindue (kvarter) omkring de funktioner, der er registreret af Shi-Tomasi, og antage, at alle ni punkter har samme bevægelse.

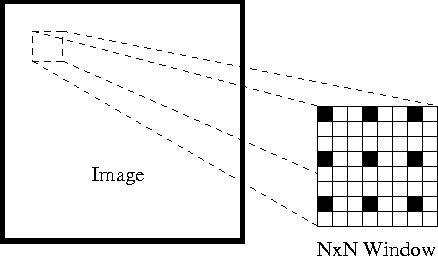
dette kan repræsenteres som

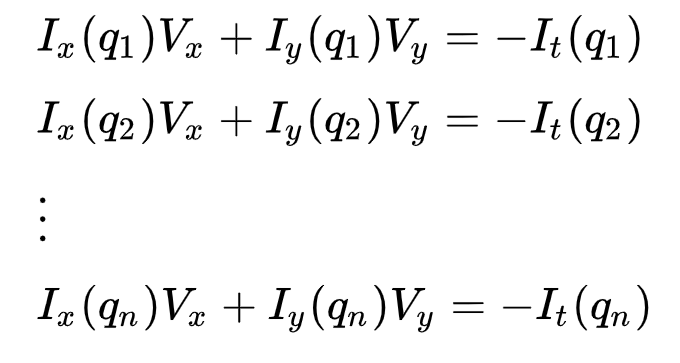
hvor \(k_1, k_2, …, k_n\) angiver billedpunkterne inde i vinduet (f.eks. \(N\) = 9 for et 3H3-vindue) og \(i_k(k_i)\), \(i_y(k_i)\) og \(i_t(k_i)\) angiver de partielle derivater af billedet \(i\) med hensyn til position \((K, Y)\) og tid \(t\), for punkt \(k_i\) på det aktuelle tidspunkt.

Dette er kun den optiske Strømningsligning (som vi beskrev tidligere) for hver af N-billedpunkterne.

sættet af ligninger kan være repræsenteret i følgende matricsform, hvor \(Av = b\):

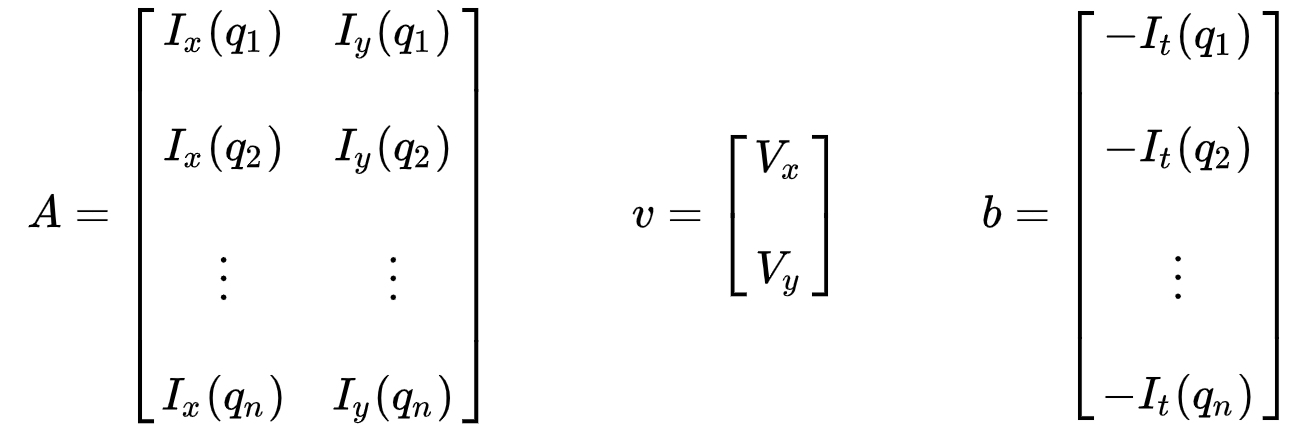
vær opmærksom på det tidligere (se “hvad er optisk strømning?”sektion) stod vi over for spørgsmålet om at skulle løse for to ukendte variabler med en ligning. Vi står nu over for at skulle løse for to ukendte (\(V_h\) og \(V_y\)) med ni ligninger, som er overbestemt.

for det andet, for at løse det overbestemte problem, anvender vi mindst kvadrater, der passer til at opnå følgende to-ligning-to-ukendt problem:

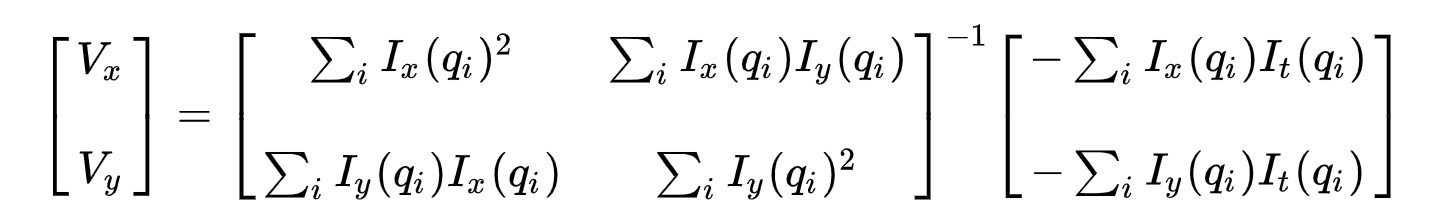
hvor \(VH = u = DH/dt\) angiver bevægelsen af \(H\) over tid og \(vy = v = dy/dt\) angiver bevægelsen af Y over tid. Løsning for de to variabler fuldender det optiske strømningsproblem.

i en nøddeskal identificerer vi nogle interessante funktioner til at spore og iterativt beregne de optiske strømningsvektorer for disse punkter. Imidlertid fungerer vedtagelsen af Lucas-Kanade-metoden kun for små bevægelser (fra vores oprindelige antagelse) og mislykkes, når der er stor bevægelse. Derfor vedtager OpenCV-implementeringen af Lucas-Kanade-metoden pyramider.

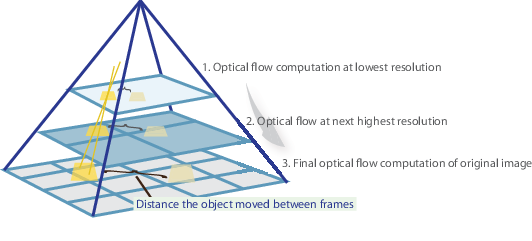
i en visning på højt niveau forsømmes små bevægelser, når vi går op ad pyramiden, og store bevægelser reduceres til små bevægelser-vi beregner optisk strømning sammen med skala. En omfattende matematisk forklaring på opencvs implementering kan findes i Bouguets noter, og dokumentationen til Opencvs implementering af Lucas-Kanade-metoden via calcOpticalFlowPyrLK() kan findes her.

visualisering

og det er det! Åbn Terminal og kør

python sparse-starter.py

for at teste din sparsomme optiske strømningsimplementering. hvis du har gået glip af nogen kode, kan den fulde kode findes i sparse-solution.py.

implementering af tæt optisk strøm

Vi har tidligere beregnet den optiske strøm for et sparsomt funktionssæt af billedpunkter. Tæt optisk strøm forsøger at beregne den optiske strømningsvektor for hvert punkt i hver ramme. Mens en sådan beregning kan være langsommere, giver den et mere nøjagtigt resultat og et tættere resultat, der er egnet til applikationer såsom læringsstruktur fra bevægelse og videosegmentering. Der er forskellige implementeringer af tæt optisk strømning. Vi bruger Farneback-metoden, en af de mest populære implementeringer, med at bruge OpenCV, et open source-bibliotek med computervisionalgoritmer, til implementering.

opsætning af dit miljø

Hvis du ikke allerede har gjort det, skal du følge trin 1 i implementeringen af sparsom optisk strøm for at konfigurere dit miljø.

næste, åben dense-starter.py med din teksteditor. Vi skriver al koden i denne Python-fil.

konfiguration af OpenCV til at læse en video

Farneback optisk strøm

Gunnar Farneback foreslog en effektiv teknik til at estimere bevægelsen af interessante funktioner ved at sammenligne to på hinanden følgende rammer i hans papir to-Frame Bevægelsesestimering baseret på polynomisk ekspansion.

først tilnærmer metoden vinduerne (se Lucas Kanade sektion af sparsom optisk strømningsimplementering for flere detaljer) af billedrammer ved kvadratiske polynomer gennem polynomisk ekspansionstransformation. For det andet ved at observere, hvordan polynomet transformeres under oversættelse (bevægelse), defineres en metode til at estimere forskydningsfelter fra polynomekspansionskoefficienter. Efter en række forbedringer beregnes tæt optisk strømning. Farnebacks papir er ret kortfattet og ligetil at følge, så jeg anbefaler stærkt at gå gennem papiret, hvis du gerne vil have en større forståelse af dens matematiske afledning.

til opencvs implementering beregner den størrelsen og retningen af optisk strømning fra et 2-kanals array af strømningsvektorer \((DH/dt, dy/dt)\), det optiske strømningsproblem. Det visualiserer derefter vinklen (retning) af strømning efter nuance og afstanden (størrelse) af strømning efter værdi af HSV-farvepræsentation. Styrken af HSV er altid indstillet til maksimalt 255 for optimal synlighed. Dokumentationen af opencvs implementering af Farneback-metoden via calcOpticalFlowFarneback() kan findes her.

visualisering

og det er det! Åbn Terminal og kør

python dense-starter.py

for at teste din tætte optiske strømningsimplementering. hvis du har gået glip af nogen kode, kan den fulde kode findes i dense-solution.py.

optisk strøm ved hjælp af dyb læring

mens problemet med optisk strømning historisk har været et optimeringsproblem, har nylige tilgange ved anvendelse af dyb læring vist imponerende resultater. Generelt tager sådanne tilgange to videobilleder som input til output af den optiske strømning (farvekodet billede), som kan udtrykkes som:

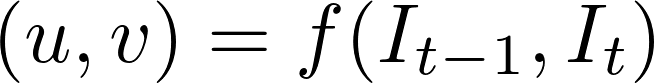
hvor \(u\) er bevægelsen i \(Y\) retningen, \(v\) er bevægelsen i \(y\) retningen, og \(f\) er et neuralt netværk, der tager i to på hinanden følgende rammer \(I_{t-1}\) (ramme på tid = \(t-1)\) og \(I_t\) (ramme på tid = \(t)\) som input.

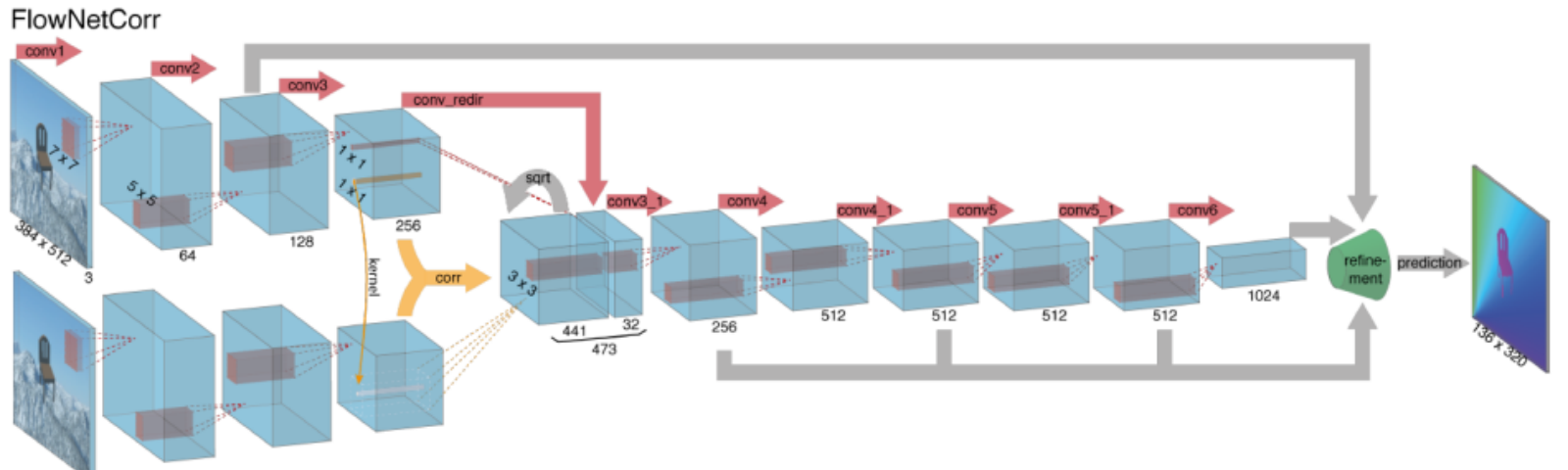
beregning af optisk strømning med dybe neurale netværk kræver store mængder træningsdata, som er særligt vanskelige at opnå. Dette skyldes, at mærkning af videooptagelser til optisk strømning kræver nøjagtigt at finde ud af den nøjagtige bevægelse af hvert punkt i et billede til subpikselnøjagtighed. For at løse spørgsmålet om mærkning af træningsdata brugte forskere computergrafik til at simulere massive realistiske verdener. Da verdener genereres ved instruktion, er bevægelsen af hvert punkt i et billede i en videosekvens kendt. Nogle eksempler på sådanne inkluderer MPI-Sintel, en open source CGI-film med optisk strømningsmærkning gengivet til forskellige sekvenser, og flyvende stole, et datasæt med mange stole, der flyver over Tilfældige baggrunde også med optisk strømningsmærkning.

løsning af optiske strømningsproblemer med dyb læring er et ekstremt varmt emne i øjeblikket med varianter af strømnet, SPyNet, PV-Net og mere, der hver især overgår hinanden på forskellige benchmarks.

optisk Strømningsapplikation: semantisk segmentering

det optiske strømningsfelt er en stor mine af information til den observerede scene. Efterhånden som teknikkerne til nøjagtig bestemmelse af optisk strømning forbedres, er det interessant at se anvendelser af optisk strømning i krydset med flere andre grundlæggende computervisionsopgaver. For eksempel er opgaven med semantisk segmentering at opdele et billede i en række regioner svarende til unikke objektklasser, men alligevel er tæt placerede objekter med identiske strukturer ofte vanskelige for segmenteringsteknikker med en ramme. Hvis objekterne placeres separat, kan objekternes forskellige bevægelser imidlertid være meget nyttige, hvor diskontinuitet i det tætte optiske strømningsfelt svarer til grænser mellem objekter.

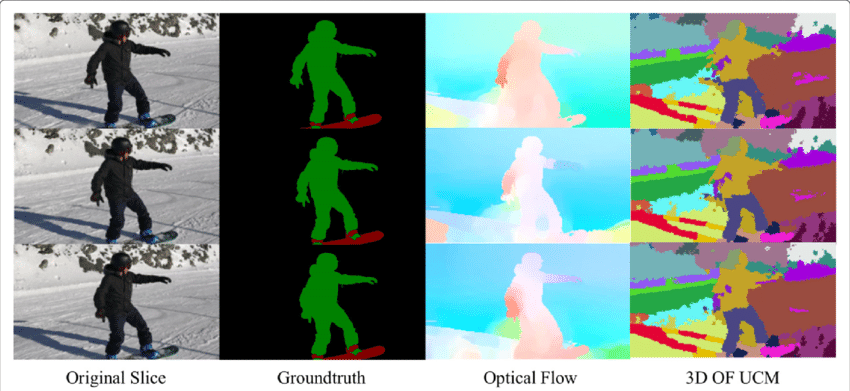
optisk Strømningsapplikation: objektdetektering & sporing

en anden lovende anvendelse af optisk strømning kan være med objektdetektering og-sporing eller i en form på højt niveau mod opbygning af realtids køretøjssporings-og trafikanalysesystemer. Da sparsom optisk strømning bruger sporing af interessepunkter, kan sådanne realtidssystemer udføres ved hjælp af funktionsbaserede optiske strømningsteknikker fra enten fra et stationært kamera eller kameraer, der er fastgjort til køretøjer.

konklusion

grundlæggende fungerer optiske strømningsvektorer som input til et utal af opgaver på højere niveau, der kræver sceneforståelse af videosekvenser, mens disse opgaver yderligere kan fungere som byggesten til endnu mere komplekse systemer såsom ansigtsudtryk analyse, autonom køretøjsnavigation og meget mere. Nye applikationer til optisk strømning, der endnu ikke er opdaget, er kun begrænset af dets designers opfindsomhed.

doven til kode, vil du ikke bruge på GPU ‘ er? Gå over til Nanonets og bygg computer vision Modeller Gratis!