uden opsyn Bayesiansk Inferens (reduktion af dimensioner og opgravning funktioner)
Lav-niveau feature detection ved hjælp af kanter

Endelig, i det øjeblik du har alle ventet på, den næste i vores uovervåget Bayesiansk inferens serie: Vores (ikke så) dybt dyk ned i den Sobel Operatør.
en virkelig magisk kantdetekteringsalgoritme, det muliggør ekstraktion på lavt niveau og dimensionalitetsreduktion, hvilket i det væsentlige reducerer støj i billedet. Det har været særligt nyttigt i ansigtsgenkendelsesapplikationer.1968-kærlighedsbarnet til Irvin Sobel og Gary Feldman (Stanford Artificial Intelligence Laboratory), denne algoritme var inspiration fra mange moderne kantdetekteringsteknikker. Ved at samle to modstående kerner eller masker over et givet billede (f. eks. se nedenfor-venstre) (hver i stand til at detektere enten vandrette eller lodrette kanter), kan vi skabe en mindre støjende, udglattet repræsentation (se nedenfor-højre).
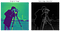
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel værdier (normalt luminans) ved at differentiere forskellen mellem hvert punktpunkt (ankerpunktet) og dets omgivende punkter (i det væsentlige tilnærme derivatet af et billede).
dette resulterer i udjævning af det originale billede og producerer en lavere dimension output, hvor geometriske funktioner på lavt niveau kan ses tydeligere. Disse udgange kan derefter bruges som input til mere komplekse klassificeringsalgoritmer eller som eksempler, der bruges til uovervåget probabilistisk klyngedannelse via Kullback-Leibler divergens (KLD) (som det ses i min nylige blog på LBP).
generering af vores lavere dimension output kræver, at vi tager derivatet af billedet. For det første beregner vi derivatet i både K og y retninger. Vi skaber to 3H3 kerner (se matricer) med nuller langs midten af den tilsvarende akse, to i midterfirkanterne vinkelret på det centrale nul og dem i hvert af hjørnerne. Hver af de ikke-nulværdier skal være positiv øverst / til højre for nullerne (afhængig af akse) og negativ på deres tilsvarende side. Disse kerner er opkaldt GH og Gy.
disse vises i formatet:
disse kerner vil derefter samle sig over vores billede og placere det centrale punkt på hver kerne over hvert punkt på billedet. Vi bruger multiplikation af matricen til at beregne intensitetsværdien af et nyt tilsvarende billedpunkt i et outputbillede for hver kerne. Derfor ender vi med to outputbilleder (en for hver kartesisk retning).
målet er at finde forskellen/ændringen mellem billedpunktet i billedet og alle billedpunkter i gradientmatricen (kerne) (GH og Gy). Mere matematisk kan dette udtrykkes som.
side note:
Vi er teknisk set ikke convolving noget. Selvom vi gerne henviser til ‘omvæltninger’ i AI-og maskinindlæringskredse, ville en omvæltning involvere at vende det originale billede. Matematisk set, når vi henviser til svingninger, beregner vi virkelig krydskorrelationen mellem hvert 3H3-område af input og masken for hvert punkt. Outputbilledet er den samlede kovarians mellem masken og input. Sådan registreres kanterne.
tilbage til vores Sobel forklaring …
de beregnede værdier for hver matrice-multiplikation mellem masken og 3H3-sektionen af indgangen summeres for at producere den endelige værdi for billedpunktet i outputbilledet. Dette genererer et nyt billede, som indeholder oplysninger om tilstedeværelsen af lodrette og vandrette kanter til stede i det oprindelige billede. Dette er en geometrisk funktion repræsentation af det originale billede. Da denne operatør garanteres at producere den samme output hver gang, giver denne teknik mulighed for stabil kantdetektering til billedsegmenteringsopgaver.
fra disse udgange kan vi beregne både gradientstørrelsen og gradientretningen (ved hjælp af arctangentoperatøren) ved et givet punkt (H, y):
herfra kan vi konstatere,at disse billedpunkter med store størrelser er mere tilbøjelige til at være en kant i billedet, mens retningen informerer os om kantretningen (selvom retningen ikke er nødvendig for at generere vores output).
en simpel implementering:
Her er en simpel implementering af Sobel-operatøren i python (ved hjælp af NumPy) for at give dig en fornemmelse for processen (for alle jer spirende kodere derude).
denne implementering er en python-variant af Pseudokodeeksemplet, der sigter mod at vise, hvordan du muligvis implementerer denne algoritme, samtidig med at du demonstrerer de forskellige trin i processen.
Hvorfor er vi ligeglade?
selvom gradienttilnærmelsen produceret af denne operatør er relativt rå, giver den en ekstremt beregningseffektiv metode til beregning af kanter, hjørner og andre geometriske træk ved billeder. Til gengæld har det banet vejen for en række dimensionalitetsreduktion og funktionsekstraktionsteknikker, såsom lokale binære mønstre (se min anden blog for flere detaljer om denne teknik).at stole på udelukkende geometriske funktioner risikerer at miste vigtige oplysninger under kodningen af vores data, men afvejningen er det, der muliggør hurtig forbehandling af dataene og til gengæld hurtig træning. Derfor er denne teknik især nyttig i scenarier, hvor tekstur og geometriske træk kan betragtes som meget vigtige for at definere input. Dette er grunden til, at ansigtsgenkendelse kan afsluttes med en relativt høj grad af nøjagtighed ved hjælp af Sobel-operatøren. Imidlertid er denne teknik muligvis ikke det bedste valg, hvis man prøver at klassificere eller gruppere input, der bruger farve som deres vigtigste differentierende faktor.
denne metode er stadig ekstremt effektiv til at opnå en lavdimensionel repræsentation af geometriske træk og et fremragende udgangspunkt for dimensionalitet og støjreduktion, inden du bruger andre klassifikatorer eller til brug i Bayesian inferensmetoder.