sendt juni 2008.
den anden af to kolonner på matematik af opmåling (den første er her). …
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
John Eggers
University of California, San Diego
jeggers ved ucsd.edu
 Mail til en ven Mail til en ven |
 Mail til en ven Mail til en ven |
 udskriv denne artikel udskriv denne artikel |
et planimeter er et bordinstrument til måling af områder, normalt områder med uregelmæssige regioner på et kort eller fotografi. De var engang almindelige, men er nu stort set blevet erstattet af digitale værktøjer.
følgende billede giver en ide om opsætningen. Polarmen roterer frit rundt om stangen, som er fastgjort på bordet. Sporarmen roterer rundt om drejetappen, hvor den forbinder polararmen. Du sporer en kurve i urets retning med sporeren, og når du gør det, ruller målehjulet sammen, og den samlede afstand, det ruller, akkumuleres på drejeknappen. Støttehjulet holder sagen fra at floppe over. I slutningen læser du et nummer fra skiven, og efter multiplikation med en faktor, der kun afhænger af planimeterets særlige konfiguration, får du området inde i kurven.

Den næste figur giver dig et bedre overblik over mekanismen.

vi kalder vognen samling af hjul, urskive og pivot. På det næste billede får du et bedre kig på det og kan se ormdrevet, der får skiven til at rotere, når målehjulet bevæger sig.

Her er diagrammet af det oprindelige planimeter, fra artiklen af Jakob Amsler, der introducerede det:
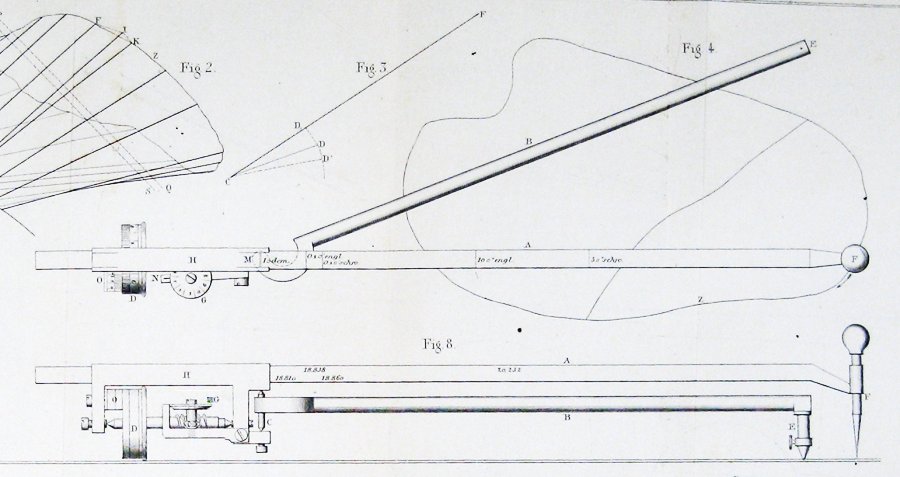
hvordan kan en sådan simpel ting måle områder?
Planimeterets geometri
planimeterets bevægelse med uret er den modsatte retning af, hvad matematikere har besluttet, skal være positiv rotation. I stedet for at overtræde denne konvention skal vi fra nu af arbejde med en matematikers planimeter, hvor du bevæger dig mod uret. Ligesom andre matematikeres fantasier er der ingen på planeten!
der er nogle begrænsninger for, hvordan du placerer planimeteret i forhold til den kurve, du vil spore. Vognen kan glide langs sporarmen, men i alle tilfælde er længden l af sporarmen mindre end længden r af polarmen. Dette betyder, at sporstoffet aldrig kan komme inden for en afstand r – l af stangen. På den anden side, når den er helt udvidet, kan sporeren aldrig nå ud over r + l. så kurven, der skal spores, skal ligge inden for ringringen mellem to cirkler, den ene med radius r – l, den anden r + l.

faktisk skal det blive klart i et øjeblik, at armene aldrig skal forlænges helt, så kurven, der skal spores, skal ligge helt inde i annulus. Desuden er stangen normalt placeret på ydersiden af kurven.

for et givet punkt i annulus er der nøjagtigt to mulige konfigurationer af planimeteret, der placerer sporeren på det punkt. At vælge et punkt eller det andet betyder at vælge et tegn til en kvadratrod. Vi kalder dette at vælge en orientering for planimeteret. Det er positivt, hvis kvadratroden er positiv. Når en orientering er valgt, forbliver den den samme, medmindre armen er helt udstrakt. Dette må aldrig ske. Så længe din kurve er helt inden for annulus, vil planimeterets konfigurationer variere jævnt og unikt med sporets sti.
den næste ting at gøre er at forstå et par ting om målehjulets bevægelse. Som det følgende billede viser, hvis hjulet bevæger sig i en lige linje en afstand C, roterer hjulet gennem en vinkel, hvor R er dens radius.

så det er virkelig sandt, at rotationen af hjulet og den tilbagelagte afstand af sporarmen har noget forhold til hinanden. Men dette forhold er lidt subtilt. Hvis armen bare bevæger sig lige frem en afstand C, området fejet ud vil være lC, men hvis det skifter parallelt med sig selv området fejet ud vil være 0. I det første tilfælde bevæger et punkt på hjulets omkreds afstand C. I det andet tilfælde bevæger hjulet sig slet ikke. Og hvis armen oversætter skråt, vil hjulet rotere en afstand svarende til højden af parallelogrammet, der er dækket af armen. I alle tilfælde, hvor armen oversættes parallelt med sig selv, vil det område, der fejes ud af den del af sporarmen mellem drejetappen og sporvognen, være lig med lC, hvor C er afstanden målt ved hjulets rotation. Dette er den grundlæggende kendsgerning, der vedrører armens bevægelse til målehjulets bevægelse.

vejen til at sætte dette præcist er, at uanset hvordan armen bevæger sig, er afstanden målt af hjulet stiintegralen

hvor Krishna er den sti, der er rejst ved armens punkt, hvor målehjulet er fastgjort, n er enhedsvektoren vinkelret på det punkt, hvor målehjulet er fastgjort, og hvor det er arm til enhver tid, og t er enhedsvektoren, der peger i kørselsretningen (således at for eksempel hvis armen bevæger sig parallelt med sig selv, er prikproduktet af N og T 0).
Guldins sætning
Dernæst skal vi forsøge at gøre planimeterets opførsel intuitivt klar, men først skal vi se på en speciel slags planimeter og i dette tilfælde bevise et mere generelt resultat. Antag, at vi tager en enkelt frit bevægelig arm med længde l og fastgør det et målehjul med radius R lige i midten.

så bevæger vi armen rundt på flyet. Hvis målehjulet roterer gennem en totalvinkel på karrus radianer, når armen bevæger sig rundt, er afstanden et punkt på omkredsen C = kr.
Guldins sætning. I denne situation er det samlede areal fejet ud af armen produktet lC.
område her fortolkes med et tegn. Hvis armen bare roterer rundt om midten, går den ene halvdel af armen fremad og den anden bagud, og de to annullerer.
Vi har allerede set, at Guldins påstand er gyldig i tilfælde af, at armen bare oversætter. Selvfølgelig sker det ikke altid – armen kan rotere, når den bevæger sig såvel som oversætter. Men vi kan se, hvad der sker ved at hugge det fejede område op som følger:

fordi målehjulet er i midten af armen, når armen roterer, klemmer den de små blokke på den ene side, når den udvider dem på den anden. Disse effekter annullerer hinanden nøjagtigt.
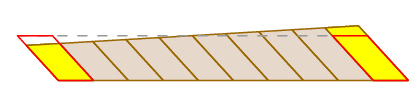
et fuldstændigt strengt bevis kan gives ved hjælp af formlen til ændring af variabler i et dobbelt integreret og udtrykket for hjulkørsel som en stiintegral.
Antag nu, at hjulet er placeret et andet sted. Sig, at dens position er c + v, hvor c er midten af armen, og v en vektor langs armen. Længden af v vil forblive fast, siger på kr. Stien, som hjulet følger, er c ( t) + v(t). Stiintegralet er nu
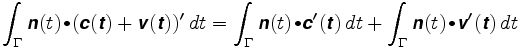
den første integral er den afstand, hjulet ville køre, hvis det var i midten af armen. I det andet er vektoren v(t) altid vinkelret på n, og v (t) har konstant længde. Vektoren v (t) bevæger sig rundt på en cirkel med radius svarende til kr. Derfor er prikkeproduktet af n og v'(t) kun den underskrevne længde af v'(t), og det andet integral er lig med kilogram gange armens samlede rotation. Derfor:
hvis hjulet er i afstand fra midten af armen, er afstanden C, som hjulet måler, C0, den afstand, der ville blive målt, hvis hjulet var i midten, plus liter gange den samlede vinkel, som armen roterer.
Du kan straks se et enkelt tilfælde af dette ved at dreje armen rundt om midten. Ved at kombinere dette med Guldins sætning ser vi det i alle tilfælde:
C = C0 + liter
område fejet ud = l C0 = l c – l liter
det fulde resultat
guldins formel giver et underskrevet område – hvis du fejer baglæns over et område, går hjulet baglæns, og du annullerer det område, du allerede har dækket. Hvis vi anvender dette på det tilfælde, hvor den frie arm kommer tilbage nøjagtigt til, hvor den startede, ser vi, at lC er lig med det område af det lukkede område, der spores ud af højre ende af armen minus det område, der fejes ud af den venstre.
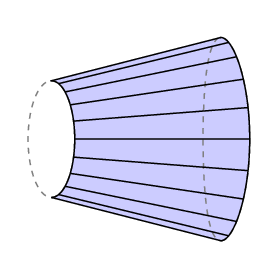
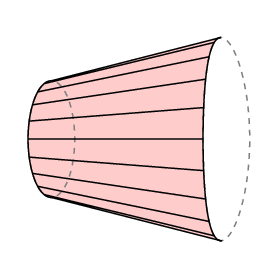

i tilfælde af polar planimeter er bunden af armen begrænset til en bue af cirklen af radius r med center ved stangen, derfor er l C området for den polære planimeter, der er sporet af sporeren. Desuden ligger stangen normalt uden for det område, der skal måles, og i dette tilfælde skal armens samlede rotationsmængde være 0. Så i dette tilfælde har vi
område af regionen sporet = lC
Her er figuren inkluderet af Jakob Amsler, opfinderen, i hans originale papir om det instrument, han opfandt:
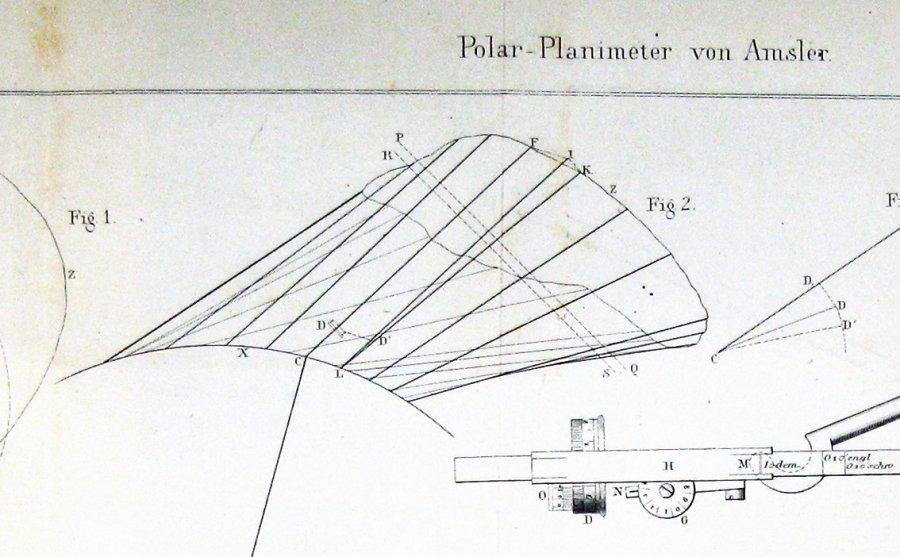
det ser ud til, at Amsler afledte sin konstruktion gennem en eller anden form for Guldins sætning.
Planimetre og greens sætning
som vi allerede har nævnt, har vi valgt planimeterets orientering, planimeterkonfigurationen er en kontinuerlig funktion af sporingspositionen. Sig, at vi vælger den positive orientering. Derefter kan vi vedhæfte til hvert punkt i annulus en enhedsvektor n, den ene peger mod uret og vinkelret på sporarmen ved sporeren.
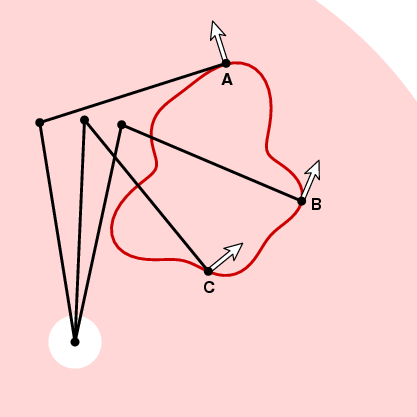
hvordan målehjulet skal reagere på bevægelse langs kurven i det næste øjeblik afhænger af vinklen mellem denne vektor og enhedens tangentvektor af kurven. På A i billedet ovenfor vil målehjulet ikke bevæge sig, fordi bevægelsen langs kurven er parallel med sporarmen. Ved B hvis sporeren bevæger sig en lille afstand ds, så vil målehjulet. Og ved C vil målehjulet bevæge sig en vis afstand mellem 0 og ds. For at være præcis skal du antage, AT t er enhedens tangentvektor på et eller andet tidspunkt i kurven. Hvis sporeren bevæger afstand ds langs kurven, bevæger målehjulet på det tidspunkt en afstand d ds, hvor d = n . t, prikproduktet af enhedsvektorerne t og n. med andre ord, hvis vi bevæger os rundt om kurven, vil målehjulet bevæge sig en samlet afstand svarende til integralet af n . t ds (dot product) eller

Men da hvert punkt i annulus svarer til en unik positiv konfiguration af planimeteret, kan vi tildele en vektor n til hvert indre punkt i annulus, og det definerer derfor et vektorfelt. Kurven er grænsen for dens indre, og ved en af vores antagelser er dette udelukkende indeholdt i det område, hvor n er defineret. Green ‘ s sætning fortæller os, at stien integreret omkring grænsen for denne region også er lig med en bestemt integral over Kristus: Derfor
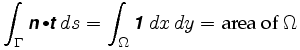
mere præcist fortæller Greens sætning os, at
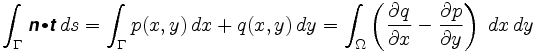
hvor n = er vektorfeltet involveret. Integranden i dobbeltintegralet kaldes vektorfeltets krølle.
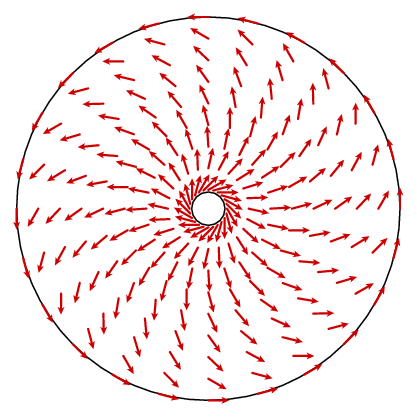
Dette synes ikke at få os meget langt. Hvad der burde ske er, at krøllen er en konstant 1. I princippet kunne vi finde en formel for vektorfeltet n og beregne dens krølle, men det er ikke meget oplysende. Vi kan dog drage fordel af en anden kendsgerning. Vektorfeltet har cirkulær symmetri, hvilket betyder, at det bestemmes af, hvad det er på en radius. Cosinus-loven giver os en simpel formel for den perifere komponent.
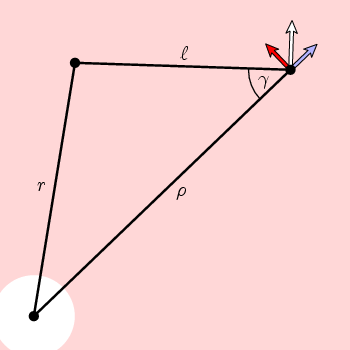
Det følger af simpel geometri i denne figur, at den periferiske komponent af n er
f(kr) = cos(kr) = (kr 2 + l 2 – r 2)/(2 kr)
det virkelige punkt i Greens sætning er, at for at kontrollere, at integranden er 1, er det tilstrækkeligt at kontrollere, at stien er integreret omkring egnede små stier er det samme som området. Til dette vælger vi vores regioner at være som her:
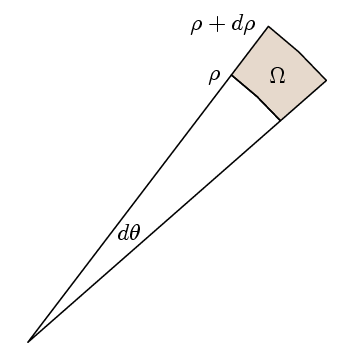
Da l gange path integral
l (ρ+dp)( f(ρ+ ∆ p)- f(ρ) ) dθ
eller
(θ/2) ( (ρ + dp) 2 – ρ 2)
der er det område i regionen Ω.
andre former for planimetre
Guldins sætning indebærer, at bevægelsen af et målehjul vil fortælle dig det område, der spores af sporeren, når armen med et målehjul på det sporer en kurve, men har den ene ende begrænset til en endimensionel kurve. Dette sker for eksempel med det rullende planimeter, hvor drejetappen er begrænset til en lige linje ved at være på en rullende cylinder.

for at finde ud af mere
-
 stadig gør og sælger planimetre.
stadig gør og sælger planimetre. - differentiel og integreret beregning Bind II, R. Courant, Blackie & Søn, 1936. Afsnittet om Guldins Formel (s.294-298) giver en forklaring på, hvordan planimeteret fungerer.
- Amslers oprindelige artikel, Vierteljahresschrift der Naturforschenden Gesellschaft i 1856. Dette mangler diagrammerne, men de er her:
- Amslers første diagram
- Amslers andet diagram
vores tak til Donna Sammis fra Stony Brook University Library for at finde artiklen og til hendes mand Robert for at levere fotografier af figurerne.
det firma, som Amsler grundlagde, producerede instrumenter langt ind i det 20.århundrede. Dette fotografi viser logoet på en strømaftagerversion af planimeteret:

- “om Planimetre”, Ingeniørforsyning. Virksomheden har også lagt en video på YouTube.
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
John Eggers
University of California, San Diego
jeggers at ucsd.edu
de, der kan få adgang til JSTOR, kan finde nogle af de ovennævnte papirer der. For dem med adgang kan American Mathematical Society ‘ s MathSciNet bruges til at få yderligere bibliografiske oplysninger og anmeldelser af nogle af disse materialer. Nogle af ovenstående emner kan fås via ACM-portalen, som også leverer bibliografiske tjenester.