introduktion
Principal Components Analysis (PCA) er en dimensionalitetsreduktionsalgoritme, der kan bruges til at fremskynde din unsupervised feature learning algoritme betydeligt. Endnu vigtigere er det, at forståelse af PCA gør det muligt for os senere at implementere blegning, hvilket er et vigtigt forbehandlingstrin for mange algoritmer.
Antag, at du træner din algoritme på billeder. Derefter vil input være noget overflødigt, fordi værdierne for tilstødende billedpunkter i et billede er stærkt korrelerede. Konkret, Antag, at vi træner på 16h16 gråtonebilleder. 256} er 256 dimensionelle vektorer, med en funktion \tekststil h_j svarende til intensiteten af hvert punkt. På grund af sammenhængen mellem tilstødende billedpunkter vil PCA give os mulighed for at tilnærme input med en meget lavere dimensionel, mens der opstår meget lidt fejl.
eksempel og matematisk baggrund
for vores løbende eksempel bruger vi et datasæt \tekststil \{1)},^{(2)}, \ldots,^{(m)}\} med \tekststil n=2 dimensionelle indgange, så \tekststil \^{(i)} \I \ Re^2. Antag, at vi vil reducere dataene fra 2 dimensioner til 1. (I praksis vil vi måske reducere data fra 256 til 50 dimensioner, siger; men ved at bruge lavere dimensionelle data i vores eksempel kan vi visualisere algoritmerne bedre.) Her er vores datasæt:
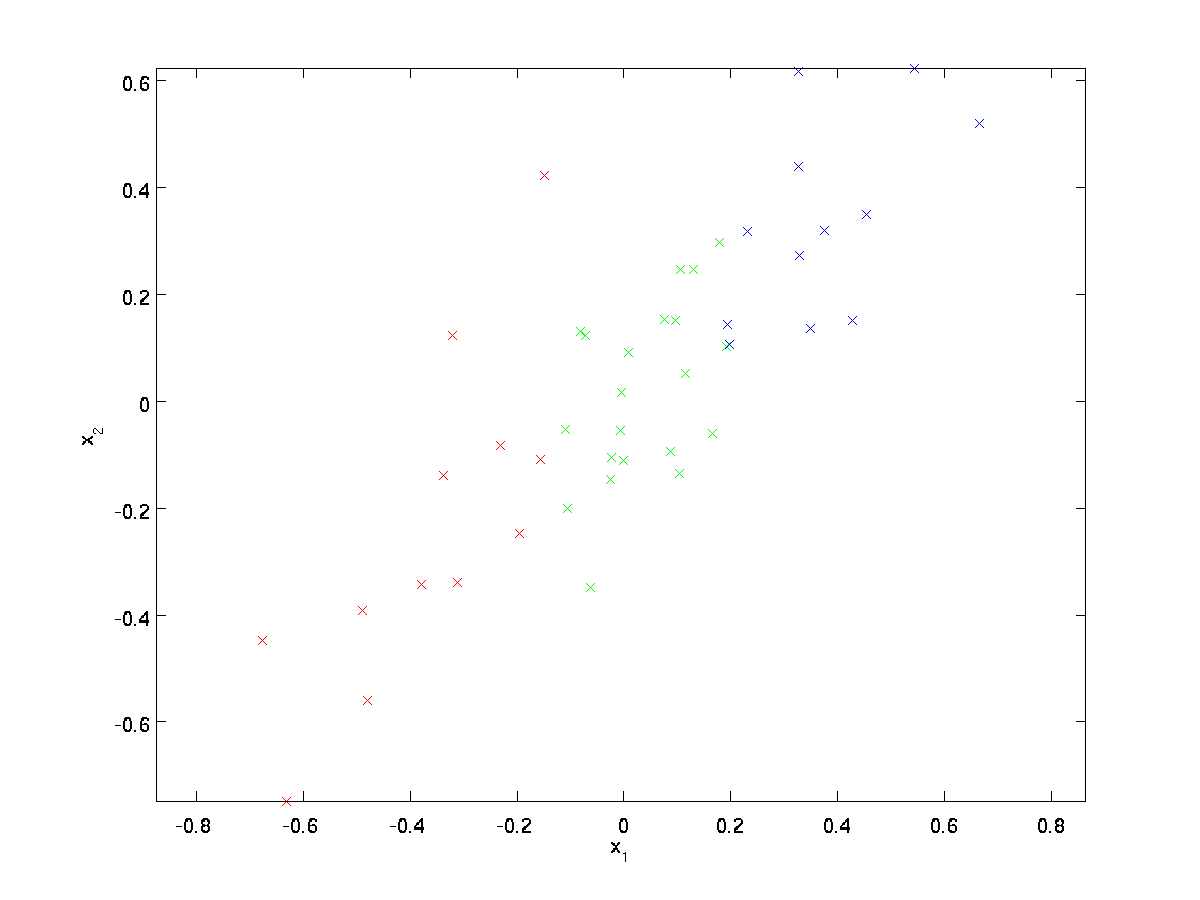
disse data er allerede forbehandlet, så hver af funktionerne \tekststyle H_1 og \tekststyle h_2 har omtrent det samme middel (nul) og varians.
med henblik på illustration har vi også farvet hvert af punkterne en af tre farver afhængigt af deres \ tekststil H_1 værdi; disse farver bruges ikke af algoritmen, og er kun til illustration.
PCA finder et lavere dimensionelt underrum, hvorpå vi kan projicere vores data.
fra visuelt at undersøge dataene ser det ud til, at \tekststyle u_1 er hovedretningen for variation af dataene, og \tekststyle u_2 den sekundære retning af variation:
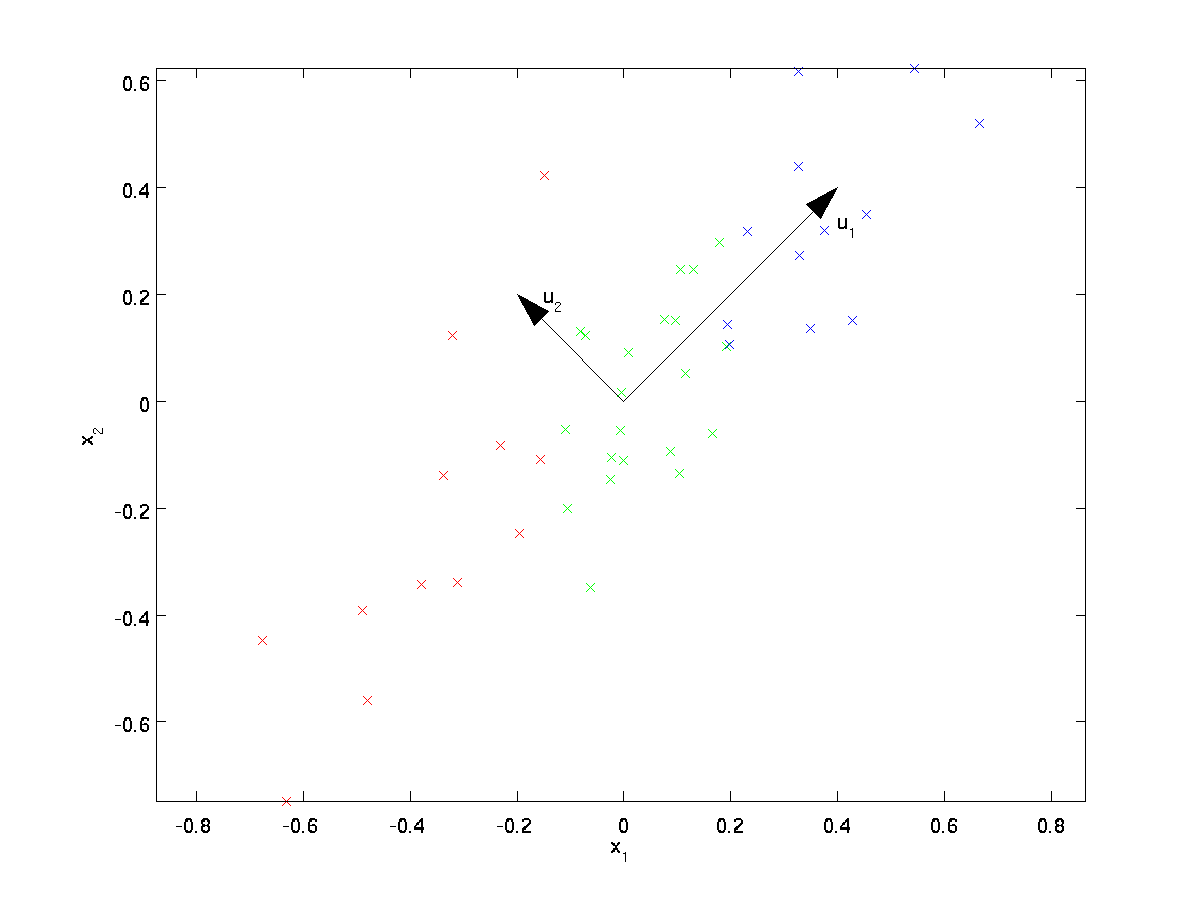
dvs., dataene varierer meget mere i retningen \tekststyle u_1 end \tekststyle u_2. For mere formelt at finde anvisningerne \ tekststyle u_1 og \ tekststyle u_2 beregner vi først matricen \ tekststyle \ Sigma som følger:
\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (h^{(i)})(H^{(i)})^T. \end{align}
Hvis \tekststyle har nul middelværdi, så er \tekststyle \Sigma nøjagtigt kovariansmatricen for \tekststyle h. (symbolet “\tekststyle \Sigma”, udtalt “Sigma”, er standardnotationen til at betegne kovariansmatricen. Desværre ser det ud som summationssymbolet, som i \sum_{i=1}^n i; men det er to forskellige ting.)
det kan derefter vises, at \ tekststyle u_1—hovedretningen for variation af dataene-er den øverste (hoved) egenvektor af \tekststyle \Sigma, og \tekststyle u_2 er den anden egenvektor.
Bemærk: Hvis du er interesseret i at se en mere formel matematisk afledning/begrundelse for dette resultat, se cs229 (Machine Learning) forelæsningsnotater om PCA (link nederst på denne side). Du behøver dog ikke at gøre det for at følge dette kursus.
Du kan bruge standard numerisk lineær algebra til at finde disse egenvektorer (se Implementeringsnotater). Konkret, lad os beregne egenvektorerne af \ tekststyle \ Sigma og stable egenvektorerne i kolonner for at danne matricen \ tekststyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
vektorerne \tekststyle u_1 og \tekststyle u_2 i vores eksempel danner et nyt grundlag, hvor vi kan repræsentere dataene. Konkret, lad \ tekststil \ i \ Re^2 være et træningseksempel. Derefter er \ tekststyle u_1^længden (størrelsen) af projektionen af \tekststyle på vektoren \tekststyle u_1.
på samme måde er \tekststyle u_2^størrelsen af \tekststyle projiceret på vektoren \tekststyle u_2.
rotation af dataene
således kan vi repræsentere \tekststil i \tekststil (u_1, u_2)-basis ved at beregne
\begin{align}H_{\rm rot} = u^t = \begin{bmatriks} u_1^TKS \\ u_2^TKS \end{bmatriks} \end{align}
(abonnementet “rot” kommer fra observationen om, at dette svarer til en rotation (og muligvis refleksion) af de oprindelige data.) Lad os tage hele træningssættet og beregne \tekststil_{\rm rot}^{(i)} = U^TK^{(i)} for hver \tekststil i. planlægning af denne transformerede data \ tekststil_ {\rm rot}, får vi:

Dette er træningssættet roteret til \tekststyle u_1,\tekststyle u_2 basis. I det generelle tilfælde vil \tekststyle U^tk være træningssættet roteret til basis \ tekststyle u_1, \ tekststyle u_2,…, \tekststyle u_n.
en af egenskaberne ved \tekststyle U er, at det er en “ortogonal” matrice, hvilket betyder, at den opfylder \tekststyle u^TU = UU^T = I. Så hvis du nogensinde har brug for at gå fra de roterede vektorer \tekststil\{\rm rot} tilbage til de originale data \tekststil\, kan du beregne
\begin{align} = u_ {\rm rot},\end{align}
fordi \tekststil U_ {\rm rot} = UU^T = H.
reduktion af Datadimensionen
Vi ser,at den primære retning for variation af dataene er datadimensionen første dimension \ tekststil_ {\rm rot, 1} af disse roterede data. Hvis vi således ønsker at reducere disse data til en dimension, kan vi indstille
\begin{align}\tilde{h}^{(i)} = H_{\rm rot,1}^{(i)} = u_1^HS^{(i)} \In \Re.\end{align}
mere generelt, hvis \tekststyle \i \Re^n og vi ønsker at reducere det til en \tekststyle k dimensionel repræsentation \tekststyle \tilde {\} \i \Re^k (hvor k < n), ville vi tage de første \tekststyle k komponenter af\tekststyle H_ {\rm rot}, som svarer til de øverste \ tekststyle k retninger af variation.
en anden måde at forklare PCA på er, at \tekststil H_{\rm rot} er en \tekststil n dimensionel vektor, hvor de første få komponenter sandsynligvis vil være store (f. eks., i vores eksempel så vi,at \tekststyle H_{\rm rot, 1}^{(i)} = u_1^TH^{(I)} tager rimeligt store værdier for de fleste eksempler \tekststyle i), og de senere komponenter er sandsynligvis små (f.eks. i vores eksempel \tekststyle H_{\rm rot, 2}^{(i)} = u_2^TH^{(i)} var mere tilbøjelige til at være små). Hvad PCA gør det det falder de senere (mindre) komponenter i \tekststyle H_{\rm rot}, og tilnærmer dem bare med 0 ‘ er. konkret kan vores definition af \tekststyle \tilde også nås ved hjælp af en tilnærmelse til \tekststyle H_ {\rm rot}, hvor alle undtagen de første \tekststyle k-komponenter er nuller. Med andre ord har vi:
\begin{align}\tilde {{\RM rot, 1}\\\vdots \ \ \ {\rm rot,k} \\0 \\ \vdots \ \ \ 0 \ \\slut {\RM rot}\ca \begin {\rm rot,1} \ \ \ vdots\\\{\rm rot,k} \\\0 \ \ \vdots \\\{\rm rot,K+1} \\ \ vdots \ \ \ {\rm rot,n} \ end {\rm rot} \ end {align}
i vores eksempel giver dette OS følgende plot af \ tekststil \ tilde{h} (ved hjælp af \ tekststil N = 2,K= 1):

da de endelige \tekststyle n-k-komponenter i \tekststyle \tilde som defineret ovenfor altid ville være nul, er der ingen grund til at holde disse nuller rundt, og derfor definerer vi \tekststyle \tilde{som en \tekststyle k-dimensionel vektor med kun de første \tekststyle k (ikke-nul) komponenter.
Dette forklarer også, hvorfor vi ønskede at udtrykke vores data i \tekststyle u_1, u_2, \ldots, u_n basis: at beslutte, hvilke komponenter der skal opbevares, bliver bare at holde de øverste \tekststyle k-komponenter. Når vi gør dette, siger vi også, at vi “bevarer de øverste \tekststyle k PCA (eller hoved) komponenter.”
Gendannelse af en tilnærmelse af dataene
nu er \ tekststyle \tilde{h} \ In \ Re^k en lavere dimensionel,” komprimeret ” repræsentation af den originale \tekststyle \in \Re^n. givet \tekststyle \tilde{h}, Hvordan kan vi gendanne en tilnærmelse \tekststyle \hat{h} til den oprindelige værdi af \tekststyle \ N? Fra et tidligere afsnit ved vi, at \tekststyle er = U ER_{\rm rot}. Desuden kan vi tænke på \ tekststyle \ tilde som en tilnærmelse til \ tekststyle \ {\rm rot}, hvor vi har indstillet de sidste \tekststyle n-k komponenter til nuller. Således kan vi med \tekststyle \tilde {\} \i \Re^k pad det ud med \tekststyle n-k nuller for at få vores tilnærmelse til\tekststyle n_ {\rm rot} \i \Re^n. endelig multiplicerer vi med \tekststyle U for at få vores tilnærmelse til \tekststyle n. konkret får vi
\begin{align} \hat{h} = u \begin{bmatriks} \ tilde{h}_1 \ \ \ vdots \ \ \ tilde{s}_k \ \ \ 0 \ \ \ vdots \\0 \ende{bmatriks} = \ sum_{i=1}^K u_i \ tilde{s}_i. \end{align}
den endelige lighed ovenfor kommer fra definitionen af \tekststil U givet tidligere. (I en praktisk implementering ville vi faktisk ikke nulpude \ tekststyle \ tilde og derefter multiplicere med \ tekststyle U, da det ville betyde at multiplicere mange ting med nuller; i stedet ville vi bare multiplicere \tekststyle \tilde \i \Re^k med de første \tekststyle k kolonner af \tekststyle U som i det endelige udtryk ovenfor.) Ved at anvende dette på vores datasæt får vi følgende plot for \ tekststyle \ hat:
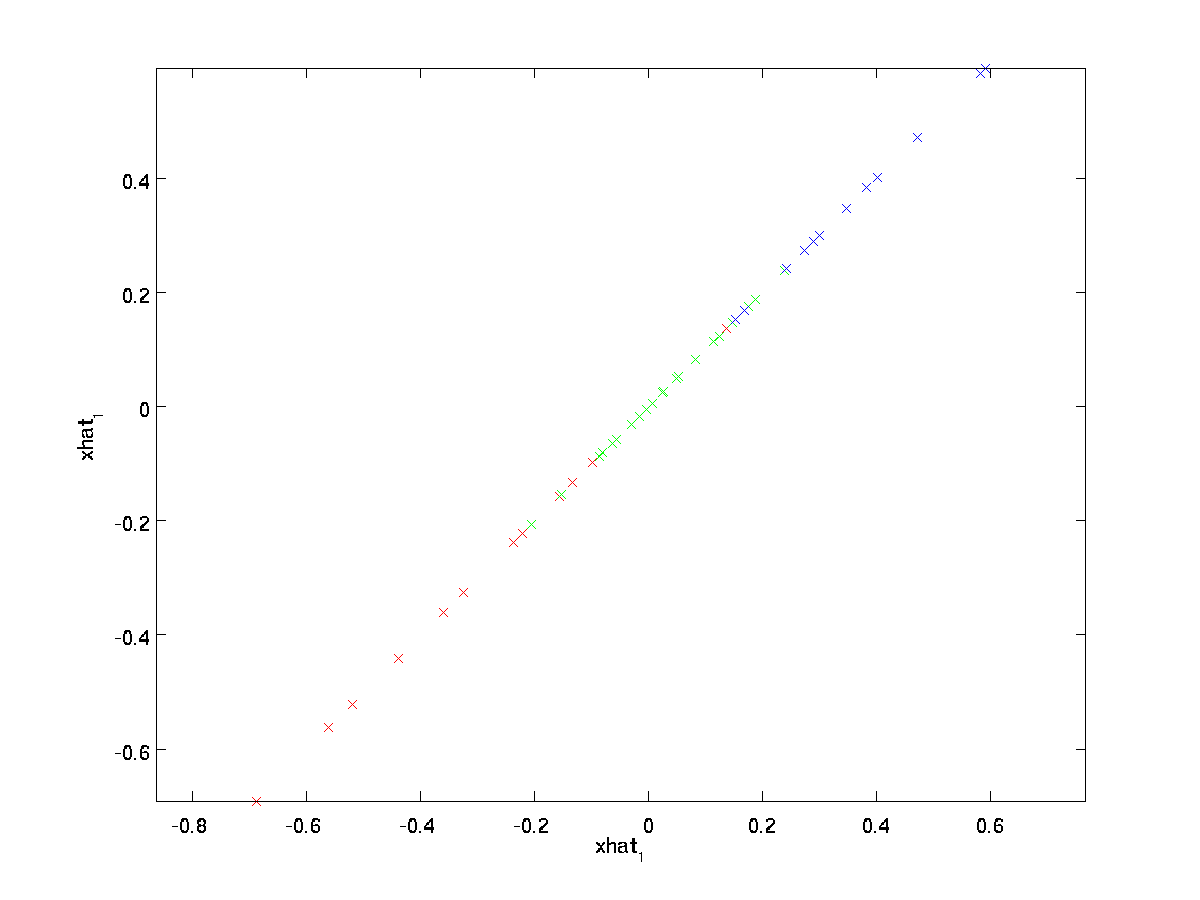
Vi bruger således en 1 dimensionel tilnærmelse til det oprindelige datasæt.
Hvis du træner en autoencoder eller en anden ikke-overvåget funktionslæringsalgoritme, afhænger driftstiden for din algoritme af inputets dimension. Hvis du fodrer \ tekststyle \ tilde\in \ Re^k ind i din læringsalgoritme i stedet for \ tekststyle, så træner du på et lavere dimensionelt input, og dermed kan din algoritme køre betydeligt hurtigere. For mange datasæt kan den lavere dimensionelle \tekststyle \tilde repræsentation være en ekstremt god tilnærmelse til originalen, og brug af PCA på denne måde kan betydeligt fremskynde din algoritme, mens du introducerer meget lidt tilnærmelsesfejl.
antal komponenter, der skal bevares
Hvordan indstiller vi \tekststil k; dvs. hvor mange PCA-komponenter skal vi beholde? I vores enkle 2 dimensionelle eksempel syntes det naturligt at beholde 1 ud af de 2 komponenter, men for højere dimensionelle data er denne beslutning mindre triviel. Hvis \ tekststyle k er for stor, vil vi ikke komprimere dataene meget; i grænsen for \tekststyle k=n, så bruger vi bare de originale data (men roteres til et andet grundlag). Omvendt, hvis \ tekststyle k er for lille, så bruger vi muligvis en meget dårlig tilnærmelse til dataene.
for at bestemme, hvordan man indstiller \tekststyle k, vil vi normalt se på “‘procentdel af varians bevaret”‘ for forskellige værdier af \tekststyle k. konkret, hvis \tekststyle k=n, så har vi en nøjagtig tilnærmelse til dataene, og vi siger, at 100% af variansen bevares. Dvs., alle variationen af de oprindelige data bevares. Omvendt, hvis \tekststyle k=0, så tilnærmer vi alle data med nulvektoren, og således bevares 0% af variansen.
mere generelt, lad \ tekststyle \ lambda_1, \ lambda_2, \ ldots, \ lambda_n være egenværdierne for \ tekststyle \ Sigma (sorteret i faldende rækkefølge), således at \ tekststyle \ lambda_j er egenværdien svarende til egenvektoren \ tekststyle u_j. så hvis vi bevarer \ tekststyle k hovedkomponenter, er procentdelen af variansen bevaret af:
\ begynd{juster} \ frac {\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}.\end{align}
i vores enkle 2D eksempel ovenfor, \tekststyle \ lambda_1 = 7.29, og \tekststyle \lambda_2 = 0.69. Ved at holde kun \tekststyle k=1 hovedkomponenter bevarede vi \tekststyle 7.29/(7.29+0.69) = 0.913, eller 91,3% af variansen.
en mere formel definition af den tilbageholdte procentdel af varians ligger uden for anvendelsesområdet for disse noter. Det er dog muligt at vise,at \tekststil \lambda_j =\sum_{i=1}^m H_{\rm rot, j}^2. 0, viser det, at \ tekststyle \ {\rm rot, j} normalt er nær 0 alligevel, og vi mister relativt lidt ved at tilnærme det med en konstant 0. Dette forklarer også, hvorfor vi bevarer de øverste hovedkomponenter (svarende til de større værdier af \tekststyle \lambda_j) i stedet for de nederste. De øverste hovedkomponenter \ RM rot, J} er dem, der er mere variable, og som får større værdier, og som vi ville pådrage os en større tilnærmelsesfejl, hvis vi skulle indstille dem til nul.
i tilfælde af billeder er en almindelig heuristisk at vælge \tekststil k for at bevare 99% af variansen. Med andre ord vælger vi den mindste værdi af \tekststil k, der opfylder
\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \gek 0.99. \end{align}
afhængigt af applikationen, hvis du er villig til at pådrage dig en ekstra fejl, bruges også værdier i området 90-98% undertiden. Når du beskriver for andre, hvordan du anvendte PCA, siger du, at du valgte \tekststyle k for at bevare 95% af variansen, vil det også være en meget lettere fortolkelig beskrivelse end at sige, at du bevarede 120 (eller hvad som helst andet antal) komponenter.
PCA på billeder
for at PCA skal fungere, ønsker vi normalt, at hver af funktionerne \tekststil H_1, h_2, \ldots, h_n skal have et lignende interval af værdier som de andre (og at have et gennemsnit tæt på nul). Hvis du har brugt PCA på andre applikationer før, kan du derfor have behandlet hver funktion separat for at have nul middelværdi og enhedsvarians ved separat at estimere middelværdien og variansen for hver funktion. Dette er dog ikke den forbehandling, som vi vil anvende på de fleste typer billeder. Med “naturlige billeder” mener vi uformelt den type billede, som et typisk dyr eller en person kan se i løbet af deres levetid.
Bemærk: Normalt bruger vi billeder af udendørs scener med græs, træer osv. 16h16) billede patches tilfældigt fra disse til at træne algoritmen. Men i praksis er de fleste funktionslæringsalgoritmer ekstremt robuste over for den nøjagtige type billede, den trænes på, så de fleste billeder taget med et normalt kamera, så længe de ikke er overdrevent slørede eller har mærkelige artefakter, skal fungere.
Når du træner på naturlige billeder, giver det ikke mening at estimere et separat gennemsnit og varians for hvert punkt, fordi statistikken i en del af billedet (teoretisk) skal være den samme som enhver anden.
denne egenskab af billeder kaldes “‘ stationaritet.”‘
for at PCA skal fungere godt, kræver vi uformelt, at (i) funktionerne har ca.nul gennemsnit, og (ii) de forskellige funktioner har lignende afvigelser til hinanden. Med naturlige billeder, (ii) er allerede tilfreds selv uden varians normalisering, og så vil vi ikke udføre nogen varians normalisering.
(Hvis du træner på lyddata-sige, på spektrogrammer—eller på tekstdata-sige, taske-af—ord vektorer-vi vil normalt ikke udføre varians normalisering enten.)
faktisk PCA er invariant til skalering af data, og vil returnere de samme egenvektorer uanset skalering af input. Mere formelt, hvis du multiplicerer hver funktionsvektor med et positivt tal (således skalerer hver funktion i hvert træningseksempel med det samme nummer), ændres PCA ‘ s output-egenvektorer ikke.
så vi bruger ikke varians normalisering. Den eneste normalisering, vi skal udføre, er gennemsnitlig normalisering for at sikre, at funktionerne har et gennemsnit omkring nul. Afhængigt af applikationen er vi ofte ikke interesserede i, hvor lyst det samlede inputbillede er. For eksempel i objektgenkendelsesopgaver påvirker billedets samlede lysstyrke ikke, hvilke objekter der er i billedet. Mere formelt er vi ikke interesserede i den gennemsnitlige intensitetsværdi af et billedplaster; således kan vi trække denne værdi ud som en form for gennemsnitlig normalisering.
konkret, hvis \tekststil^{(i)} \I \Re^{n} er (gråtoner) intensitetsværdierne for en 16h16 billedplaster (\tekststil n=256), kan vi normalisere intensiteten af hvert billede \tekststil^{(i)} som følger:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n * ^{(i)}_j^{(i)}_j : bemærk, at de to trin ovenfor udføres separat for hvert billede \tekststil \^{(i)}, og at \tekststil \mu^{(i)} her er den gennemsnitlige intensitet af billedet \ tekststil \ ^{(i)}. Dette er især ikke det samme som at estimere en middelværdi separat for hver tekststil.
Hvis du træner din algoritme på andre billeder end naturlige billeder (for eksempel billeder af håndskrevne tegn eller billeder af enkelt isolerede objekter centreret mod en hvid baggrund), kan andre typer normalisering være værd at overveje, og det bedste valg kan være applikationsafhængigt. Men når man træner på naturlige billeder, ville det være en rimelig standard at bruge den gennemsnitlige normaliseringsmetode pr.billede som angivet i ligningerne ovenfor.
hvidtning
Vi har brugt PCA til at reducere dimensionen af dataene. Der er et nært beslægtet forbehandlingstrin kaldet blegning (eller i nogle andre litteraturer sfæring), som er nødvendigt for nogle algoritmer. Hvis vi træner på billeder, er det rå input overflødigt, da tilstødende billedværdier er stærkt korrelerede. Målet med hvidtning er at gøre input mindre overflødigt; mere formelt er vores desiderata, at vores læringsalgoritmer ser et træningsinput, hvor (i) funktionerne er mindre korrelerede med hinanden, og (ii) funktionerne har alle samme varians.
2D eksempel
vi vil først beskrive blegning ved hjælp af vores tidligere 2D eksempel. Vi vil derefter beskrive, hvordan dette kan kombineres med udjævning, og endelig hvordan man kombinerer dette med PCA.
hvordan kan vi gøre vores inputfunktioner ukorrelerede med hinanden? Vi havde allerede gjort dette ved beregning af \tekststyle{\rm rot}^{(i)} = U^th^{(i)}.
gentagelse af vores tidligere figur, vores plot for \tekststil_{\rm rot} var:

kovariansmatricen af disse data er givet af:
\begin{align}\begin{bmatriks}7.29 && 0.69\ende{bmatriks}.\end{align}
(Bemærk: Teknisk set vil mange af udsagnene i dette afsnit om “kovarians” kun være sande, hvis dataene har nul gennemsnit. I resten af dette afsnit vil vi tage denne antagelse som implicit i vores udsagn. Men selvom dataens gennemsnit ikke er nøjagtigt nul, er de intuitioner, vi præsenterer her, stadig sande, og det er derfor ikke noget, du bør bekymre dig om.)
det er ikke tilfældigt, at de diagonale værdier er \tekststyle \lambda_1 og \tekststyle \lambda_2. Endvidere er de off-diagonale poster nul; således er \ tekststyle H_{\rm rot,1} og\tekststyle H_ {\rm rot,2} ukorrelerede, hvilket opfylder en af vores ønsker for hvide data (at funktionerne er mindre korrelerede).
for at få hver af vores inputfunktioner til at have enhedsvarians, kan vi simpelthen omskalere hver funktion \tekststil_{\rm rot,i} ved \tekststil 1/\kvm{\lambda_i}. Konkret definerer vi vores hvide data \ tekststil \ \RM Pcahvid} \ i \ Re^n som følger:
\begynd{juster}H_{\RM Pcahvid,i} = \frac{H_{\rm rot,i} }{\KVRT{\lambda_i}}. \end{align}
Plotting \tekststil_ {\RM Pcahvid}, vi får:

disse data har nu kovarians svarende til identitetsmatricen \tekststyle I. vi siger, at \tekststyle H_{\RM Pcahvid} er vores PCA-hvide version af dataene: de forskellige komponenter i \tekststyle H_{\rm Pcahvid} er ukorrelerede og har enhedsvarians.
blegning kombineret med dimensionalitetsreduktion. Hvis du vil have data, der er hvide, og som er lavere dimensionelle end den oprindelige indgang, kan du også eventuelt kun beholde de øverste \tekststyle k-komponenter i \tekststyle H_{\RM Pcahvid}. Når vi kombinerer PCA-blegning med regulering (beskrevet senere), vil de sidste par komponenter i \tekststil H_{\rm Pcahvid} alligevel være næsten nul og kan således sikkert tabes.endelig viser det sig, at denne måde at få dataene til at have kovariansidentitet \tekststil I ikke er unik. Konkret, hvis \tekststyle R er en ortogonal matrice, så den opfylder \tekststyle RR^T = R^TR = I (mindre formelt, hvis \tekststyle R er en rotation/refleksionsmatrice), så vil \tekststyle R\, H_{\rm Pcahvid} også have identitetskovarians.
vi vælger \tekststil R = U. vi definerer
\begin{align}S_{\rm Pcahvid} = u S_{\RM Pcahvid}\end{align}
Plotting \tekststil S_{\rm Hvid}, vi får:

det kan vises, at ud af alle mulige valg for \tekststyle r, forårsager dette valg af rotation \tekststyle H_{\RM hhv} at være så tæt som muligt på de originale inputdata \tekststyle H.
når vi bruger JSC-hvidtning (i modsætning til PCA-hvidtning), beholder vi normalt alle \Tekststyle n-dimensioner af dataene og forsøger ikke at reducere dens dimension.
Regularisaton
ved implementering af PCA-hvidtning eller SCA-hvidtning i praksis vil nogle gange Nogle af egenværdierne \tekststil \lambda_i være numerisk tæt på 0, og dermed vil skaleringstrinnet, hvor vi deler med \KVRT{\lambda_i} involvere opdeling med en værdi tæt på nul; dette kan få dataene til at sprænge (påtage sig store værdier) eller på anden måde være numerisk ustabile. I praksis implementerer vi derfor dette skaleringstrin ved hjælp af en lille mængde regulering og tilføjer en lille konstant \ tekststil \epsilon til egenværdierne, før de tager deres kvadratrod og inverse:
\begynd {{\RM Pcahvid,i} = \frac {{\rm rot,i}} {\RRT{\lambda_i + \epsilon}}.\end{align}
når \tekststyle tager værdier omkring \tekststyle , kan en værdi på \tekststyle \epsilon \ ca.10^{-5} være typisk.
i tilfælde af billeder har Tilføjelse af \tekststyle \epsilon her også effekten af let udjævning (eller lavpasfiltrering) inputbilledet. Dette har også en ønskelig effekt ved at fjerne aliasing-artefakter forårsaget af den måde, hvorpå billedpunkter er lagt ud i et billede, og kan forbedre de lærte funktioner (detaljer ligger uden for disse noter).det er en form for forbehandling af de data, der kortlægger det fra \tekststyle til \tekststyle. Det viser sig, at dette også er en grov model for, hvordan det biologiske øje (nethinden) behandler billeder. Specifikt, når dit øje opfatter billeder, vil de fleste tilstødende “billedpunkter” i dit øje opfatte meget lignende værdier, da tilstødende dele af et billede har en tendens til at være stærkt korreleret i intensitet. Det er således spild for dit øje at skulle overføre hvert punkt separat (via din optiske nerve) til din hjerne. I stedet udfører din nethinden en decorrelation operation (dette gøres via retinale neuroner, der beregner en funktion kaldet “on center, off surround/off center, on surround”), som ligner den, der udføres af SCA. Dette resulterer i en mindre overflødig repræsentation af inputbilledet, som derefter overføres til din hjerne.
implementering af PCA-blegning
i dette afsnit opsummerer vi PCA -, PCA-blegnings-og CCA-blegningsalgoritmerne og beskriver også, hvordan du kan implementere dem ved hjælp af effektive lineære algebrabiblioteker.
først skal vi sikre, at dataene har (ca.) nul-middelværdi. For naturlige billeder opnår vi dette (CA.) ved at trække middelværdien af hvert billedplaster.
Vi opnår dette ved at beregne gennemsnittet for hver patch og trække det fra for hver patch. I Matlab kan vi gøre dette ved at bruge
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);Dernæst skal vi beregne \tekststil \Sigma = \frac{1}{m} \sum_{i=1}^m (h^{(i)})(H^{(i)})^T. hvis du implementerer dette i Matlab (eller endda hvis du implementerer dette i C++ Java osv., men har adgang til et effektivt lineært algebrabibliotek), at gøre det som en eksplicit sum er ineffektivt. I stedet kan vi beregne dette i et fald som
sigma = x * x' / size(x, 2);(kontroller matematikken selv for korrekthed.) Her antager vi, at S er en datastruktur, der indeholder et træningseksempel pr.
dernæst beregner PCA egenvektorerne af \Sigma. Man kunne gøre dette ved hjælp af Matlab eig-funktionen. Men fordi \Sigma er en symmetrisk positiv semi-bestemt matrice, er det mere numerisk pålideligt at gøre dette ved hjælp af svd-funktionen. Konkret, hvis du implementerer
= svd(sigma);så vil matricen u indeholde egenvektorerne af \Sigma (en egenvektor pr.kolonne sorteret i rækkefølge fra top til bund egenvektor), og de diagonale poster i matricen s vil indeholde de tilsvarende egenværdier (også sorteret i faldende rækkefølge). Matricen V vil være lig med U, og kan sikkert ignoreres.
(Bemærk: Svd-funktionen beregner faktisk entalvektorerne og entalværdierne for en matrice, som for det specielle tilfælde af en symmetrisk positiv semi-bestemt matrice—hvilket er alt, hvad vi er bekymrede for her—er lig med dens egenvektorer og egenværdier. En fuldstændig diskussion af entalvektorer vs. egenvektorer er uden for disse notes anvendelsesområde.)
endelig kan du beregne \tekststil H_ {\rm rot} og \tekststil \ tilde{H} som følger:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepdette giver din PCA-repræsentation af dataene i form af \tekststil \tilde{h} \in \Re^k. I øvrigt, hvis det er en \tekststyle n-by-\tekststyle m-matrice, der indeholder alle dine træningsdata, er dette en vektoriseret implementering, og udtrykkene ovenfor fungerer også til beregning af{\rm rot} og \tilde{tilde} for hele din træning indstilles alt på en gang. Den resulterende H_{\rm rot} og \tilde{h} vil have en kolonne svarende til hvert træningseksempel.
for at beregne PCA-hvide data \ tekststil \ {\RM Pcahvid}, brug
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;da S ‘ S diagonal indeholder egenværdierne \tekststil \lambda_i, viser det sig at være en kompakt måde at beregne \tekststil på\{\RM Pcahvid,i} = \
endelig kan du også beregne de hvide data\tekststil\{\RM hvid} som:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;