Das Franck-Condon-Prinzip beschreibt die Intensitäten von vibronischen Übergängen oder die Absorption oder Emission eines Photons. Es besagt, dass, wenn ein Molekül einen elektronischen Übergang durchläuft, wie Ionisation, Die Kernkonfiguration des Moleküls erfährt keine signifikante Änderung. Dies liegt daran, dass Kerne viel massereicher sind als Elektronen und der elektronische Übergang schneller stattfindet, als die Kerne reagieren können. Wenn sich der Kern an die neue elektronische Konfiguration anpasst, besagt die Theorie, dass er einer Vibration ausgesetzt sein muss.
Wenn wir uns den vertikalen Übergang vom Boden zum angeregten elektronischen Zustand so vorstellen, dass er von einer Schwingungswellenfunktion ausgeht, die eine Wahrscheinlichkeitsverteilung für das Auffinden der Kerne in einem bestimmten Raumbereich ergibt, können wir die Wahrscheinlichkeit eines gegebenen Schwingungsniveaus aus dem Überlappungsintegral \(S_ {v‘,v}\) bestimmen, das die Überlappung der Schwingungswellenfunktion im Boden- und angeregten Zustand ergibt. Die \(v\) Quantenzahlen beziehen sich auf den Grundzustand und die \(v\) Quantenzahlen beziehen sich auf den angeregten Zustand. Die Übergangswahrscheinlichkeit kann mit der Condon-Approximation in elektronische und nukleare Teile getrennt werden.
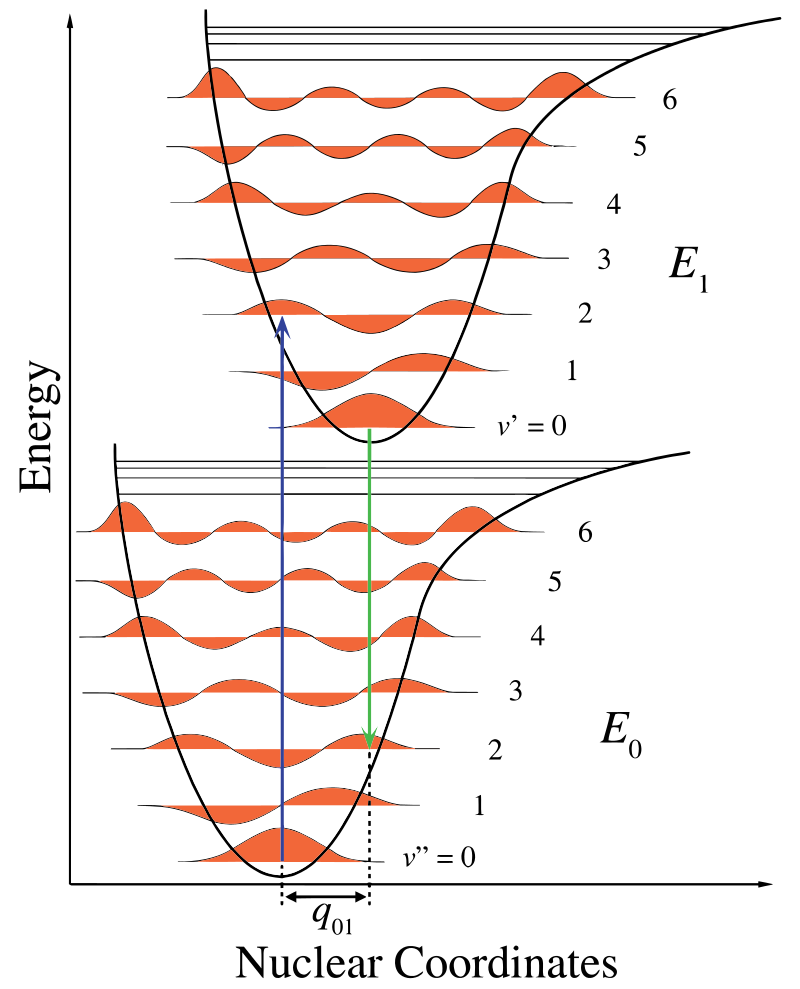
In Abbildung \(\pageIndex{1}\) zeigt die Kernachse eine Folge der internuklearen Trennung und der vibronische Übergang wird durch die blauen und grünen vertikalen Pfeile angezeigt. Diese Abbildung zeigt drei Dinge:
- Eine Absorption führt zu einem höheren Energiezustand,
- Fluoreszenz führt zu einem niedrigeren Energiezustand und
- Die Verschiebung der Kernkoordinaten zwischen dem angeregten und dem angeregten Zustand weist auf eine neue Gleichgewichtsposition für das nukleare Wechselwirkungspotential hin. Die Tatsache, dass der Fluoreszenzpfeil kürzer als die Absorption ist, zeigt an, dass er weniger Energie hat oder dass seine Wellenlänge länger ist.
Die klassische Condon-Approximation
Die Condon-Approximation ist die Annahme, dass der elektronische Übergang auf einer im Vergleich zur Kernbewegung kurzen Zeitskala stattfindet, so dass die Übergangswahrscheinlichkeit an einer festen Kernposition berechnet werden kann.
Diese Schwingungsänderung wird während eines Zustands aufrechterhalten, der als schnelle elektronische Erregung bezeichnet wird. Die resultierenden coulombschen Kräfte erzeugen ein Gleichgewicht, wie in der Abbildung für die Kerne gezeigt, die als Wendepunkt bezeichnet werden. Der Wendepunkt kann durch Zeichnen einer vertikalen Linie vom Minimum der unteren Kurve bis zum Schnittpunkt des höheren elektronischen Zustands abgebildet werden. Dieses Verfahren wird als vertikaler Übergang bezeichnet und wurde zuvor im Zusammenhang mit der Photoelektronenspektroskopie (einer anderen elektronischen Spektroskopie) diskutiert..
Das Franck-Condon-Prinzip erklärt die relativen Intensitäten von vibronischen Übergängen, indem es die Wahrscheinlichkeit eines Schwingungsübergangs mit der Überlappung der Schwingungswellenfunktionen in Beziehung setzt. Sie besagt, dass die Wahrscheinlichkeit eines auftretenden Schwingungsübergangs durch das Franck-Condon-Überlappungsintegral gewichtet wird:
\
Innerhalb der Franck-Condon-Approximation werden die Kerne während elektronischer Übergänge als „fest“ betrachtet. Somit können elektronische Übergänge als vertikale Übergänge auf elektronischen potentiellen Energiekurven betrachtet werden (vierische Übergänge in Abbildung \(\pageIndex {1}\)).
Das Quanten-Franck-Condon-Prinzip
Das Franck-Condon-Prinzip hat sowohl eine klassische als auch eine Quantenanwendung. Klassisch ist das Franck-Condon-Prinzip die Annäherung, dass ein elektronischer Übergang am wahrscheinlichsten ohne Änderungen der Positionen der Kerne in der molekularen Einheit und ihrer Umgebung auftritt. Der resultierende Zustand wird als Franck–Condon-Zustand bezeichnet, und der betreffende Übergang ist ein vertikaler Übergang. Die quantenmechanische Formulierung dieses Prinzips ist, dass die Intensität eines vibronischen Übergangs proportional zum Quadrat des Überlappungsintegrals zwischen den Schwingungswellenfunktionen der beiden am Übergang beteiligten Zustände ist.
Das Franck-Condon-Prinzip basiert auf der Born-Oppenheimer-Approximation, die die Trennung der elektronischen \(q\) und nuklearen \(Q\) Wellenfunktionen bei der Gesamtwellenfunktion ermöglicht.
\
Da der Übergangsoperator \(\hat{\mu}(q)\) nur von der elektronischen Komponente abhängig ist, können die Kernkomponenten vom Übergangsmomentintegral getrennt werden, das die Wahrscheinlichkeit des Übergangs bestimmt:
&= \Unterbügel{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nuclear overlap}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} / \psi_{el , i} \rangle \end{align}\]
Wenn das Kernüberlappungsintegral für diesen Übergang Null ist, wird der Übergang unabhängig von der Größe des elektronischen Faktors nicht beobachtet.
\(S_{00}\) Transition Evaluated within Harmonic Oscillator Model
Die Kernüberlappung für den Null-Null-Übergang \(S_{00}\) kann ganz einfach mit Hilfe der Definition der Gaußschen Form der harmonischen Oszillator-Wellenfunktionen berechnet werden.
Die Nullpunkt-Wellenfunktion im elektronischen Grundzustand ist
\
Die Nullpunkt-Wellenfunktion im angeregten elektronischen Zustand ist
\
wobei
- \(\alpha = \dfrac{\sqrt{mk}} {\hbar}\)
- \(R_e\) ist die Gleichgewichtsbindungslänge im angeregten elektronischen Zustand
- \(Q_e\) ist die Gleichgewichtsbindungslänge im angeregten elektronischen Zustand
Das Kernüberlappungsintegral ist
\
Der Exponent in Gleichung \(\ref{FC1}\) kann erweitert werden als
\
und wir verwenden
\
und
\
, um das Quadrat innerhalb des Integrals zu ersetzen und zu vervollständigen. Wir können ausdrücken
\.\]
Somit ist das Integral in Gleichung \(\ref{FC2}\)
\
Das Integral ist ein Gaußsches Integral. Sie können zeigen, dass, wenn wir \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) dann \(dz = \sqrt{\alpha} dR\) und das Integral wird
\
dieses Integral wurde bereits gelöst, aus einer Tabelle von Integralen, Gleichung \(\ref{FC3}\) wird
\
Wir würden das gleiche Verfahren anwenden, um die Überlappung der Nullenschwingung im Boden mit dem ersten angeregten Schwingungspegel des angeregten Zustands zu berechnen: \(S_{01}\).
\(S_{01}\) Übergang innerhalb des harmonischen Oszillatormodells ausgewertet
Um die Überlappung des nullten Grundzustandspegels (\(v=0\)) mit dem ersten angeregten Zustandspegel (\(v’=1\)) zu berechnen, verwenden wir das Hermite-Polynom \(H_1(x) =2x\) zur Beschreibung der angeregten Zustandswellenfunktion (siehe hier für eine Übersicht über harmonische Oszillatorwellenfunktionen). Hier \(x = \sqrt{\alpha}(R – Q_e)\).
\
mit die null-punkt wellenfunktion in die boden elektronische zustand ist
\
Die erste aufgeregt-zustand wellenfunktion in die aufgeregt elektronische zustand ist
\
Die überlappung des nullten Grundzustandsniveaus mit dem ersten angeregten Zustandsniveau (Gleichung \(\ref{FC01}\)) ist dann
\
und
\
Die gleichen Substitutionen können wie oben gemacht werden, so dass das Integral geschrieben werden kann wie (nicht gezeigt und in einer Hausaufgabe demonstriert werden Übungen) und das Endergebnis ist
\
Wir könnten fortfahren und die Überlappung der nullten Ebene im Grundzustand mit allen höheren Lichtschwingungsebenen berechnen: \(S_{02}\), \(S_{03}\) usw. Jeder Term entspricht einem Übergang mit einer anderen Energie, da die Schwingungsebenen unterschiedliche Energien haben. Die Absorptionsbande hat dann den Anschein einer Progression (einer Franck-Condon-Progression) von Übergängen zwischen verschiedenen Ebenen mit jeweils eigener Wahrscheinlichkeit.
Franck-Condon-Progressionen
Um die Bedeutung der obigen Formel für den FC-Faktor zu verstehen, untersuchen wir eine potentielle Energiefläche im Erd- und angeregten Zustand bei \(T = 0\) Kelvin. Unten sind zwei Zustände dargestellt, die durch 8.000 cm-1 Energie getrennt sind. Dies ist eine Energietrennung zwischen den Böden ihrer Potentialbrunnen, aber auch zwischen den jeweiligen Nullpunkt-Energieniveaus. Nehmen wir an, dass die Wellenzahl des Schwingungsmodus 1.000 cm-1 beträgt und dass die Bindungslänge dadurch erhöht wird, dass ein Elektron aus einem Bindungsorbital entfernt und bei elektronischer Anregung in ein Anti-Bindungsorbital gebracht wird.
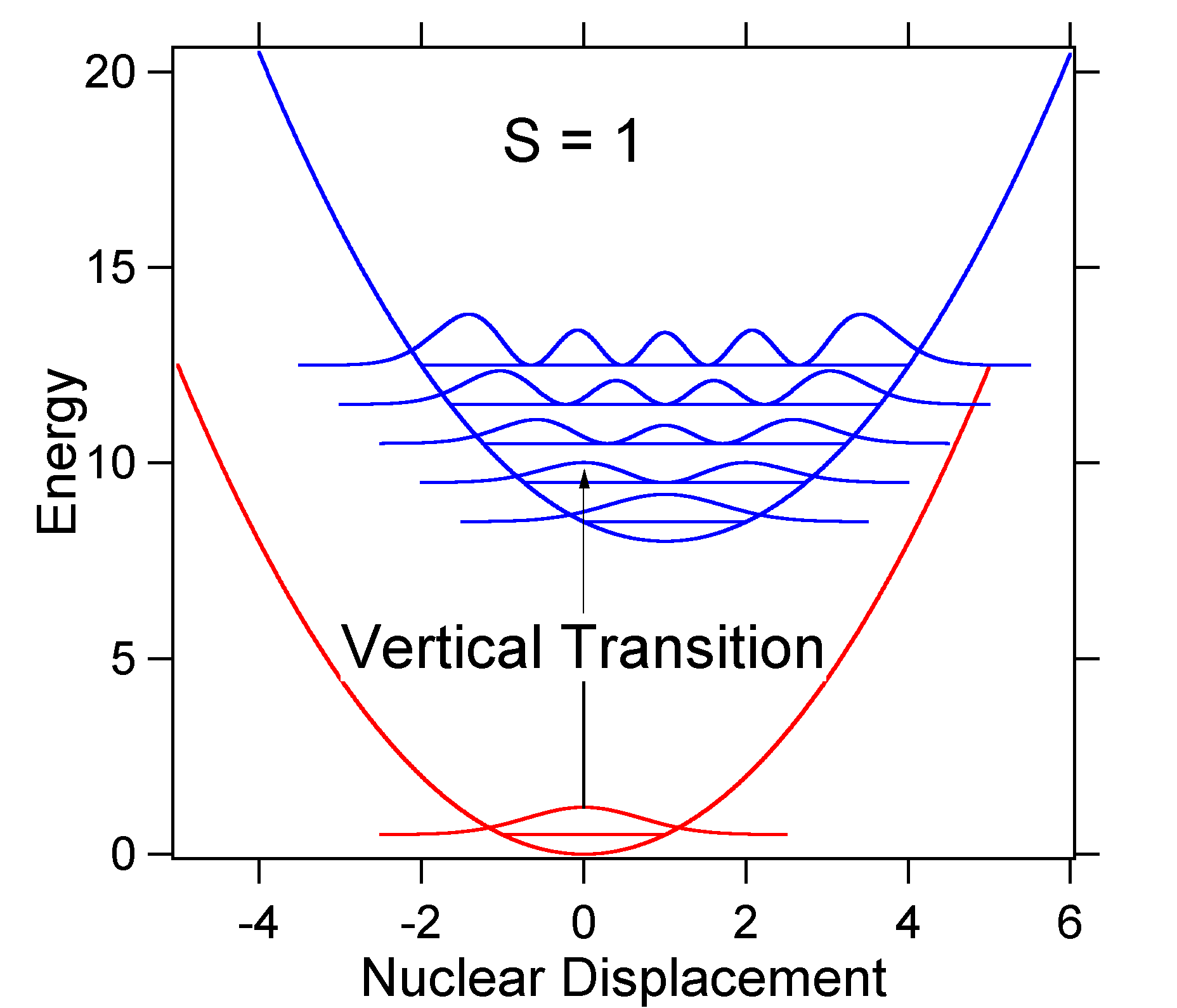
Nach dem obigen Modell für den Franck-Condon-Faktor würden wir ein „Stick“ -Spektrum erzeugen (Abbildung \(\pageIndex{3}\)), bei dem jeder Schwingungsübergang unendlich schmal ist und der Übergang nur auftreten kann, wenn \(E = h\nu\) genau. Zum Beispiel wurden die potentiellen Energieflächen für S = 1 angegeben und die Übergangswahrscheinlichkeit auf jeder Ebene wird durch die Stöcke (schwarz) in der folgenden Abbildung angegeben.
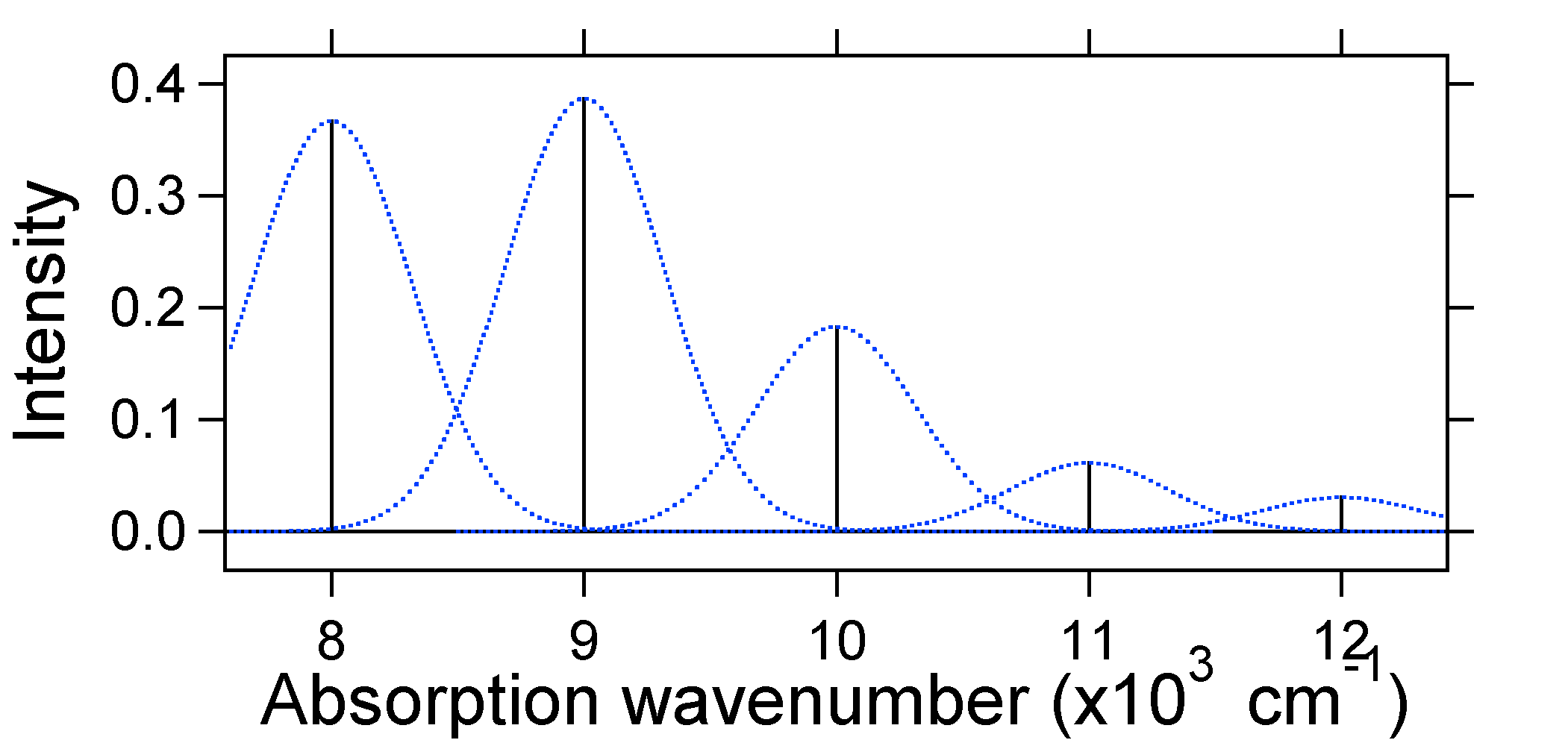
Die gepunkteten Gaußschen, die jeden Stab umgeben, geben ein realistischeres Bild davon, wie das Absorptionsspektrum aussehen sollte. An dieser ersten Stelle wird jedem Energieniveau (Stick) eine gewisse Breite durch die Tatsache gegeben, dass der Zustand eine endliche Lebensdauer hat. Eine solche Verbreiterung wird als homogene Verbreiterung bezeichnet, da sie alle Moleküle im Ensemble auf ähnliche Weise beeinflusst. Es gibt auch eine Verbreiterung aufgrund kleiner Unterschiede in der Umgebung jedes Moleküls. Diese Art der Verbreiterung wird als inhomogene Verbreiterung bezeichnet. Unabhängig vom Ursprung wurde das obige Modell unter Verwendung einer Gaußschen Verbreiterung
Die Kernverschiebung zwischen dem Grund- und angeregten Zustand bestimmt die Form des Absorptionsspektrums. Lassen Sie uns sowohl eine kleinere als auch eine große erregte Zustandsverschiebung untersuchen. If \(S = ½\) und die potentiellen Energieflächen sind in diesem Fall:
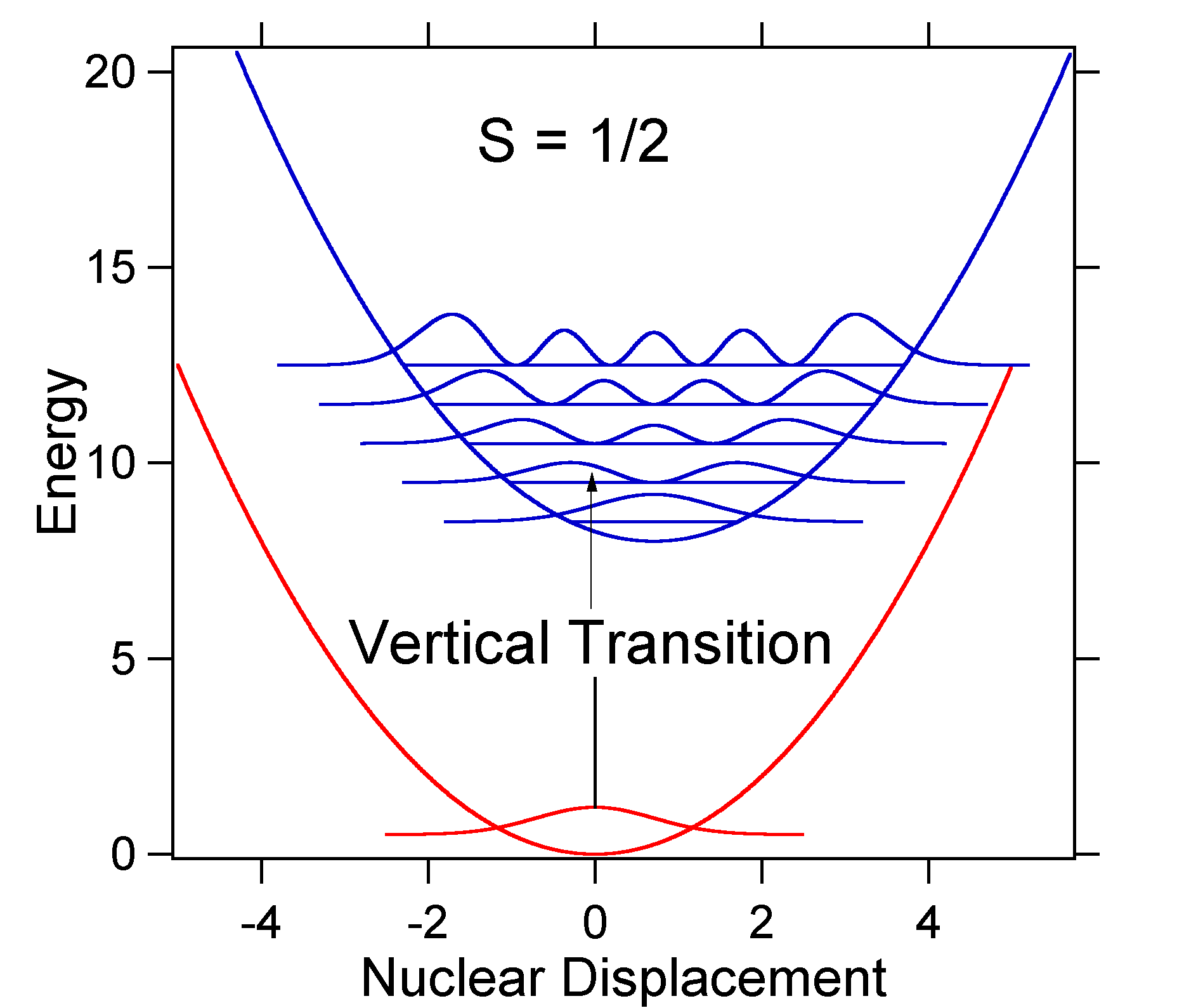
For this case the „stick“ spectrum has the appearance in Figure \(\PageIndex{5}\)
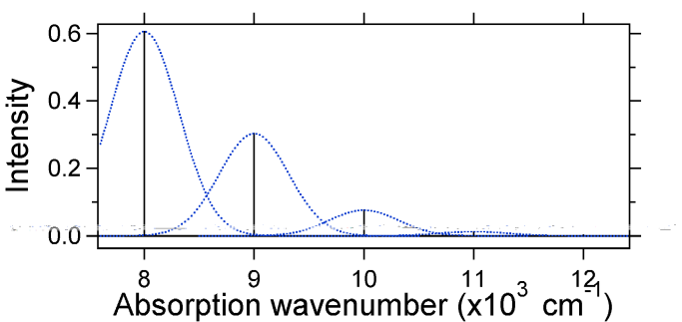
Beachten Sie, dass der Schwingungsübergang Null-Null oder \(S_{0,0}\) in dem Fall, in dem die Verschiebung klein ist, sehr groß ist.
Als allgemeine Faustregel gibt die \(S\) Konstante das Verhältnis der Intensität des \(v = 2\) Übergangs zum \(v = 1\) Übergang an. In diesem Fall ist seit \(S = 0,5\) der \(v = 2\) Übergang 0,5 die Intensität des \(v = 1\) Übergangs.
Als Beispiel für eine größere Verschiebung ist nachfolgend die Anordnung der potentiellen Energieflächen für S = 2 dargestellt.
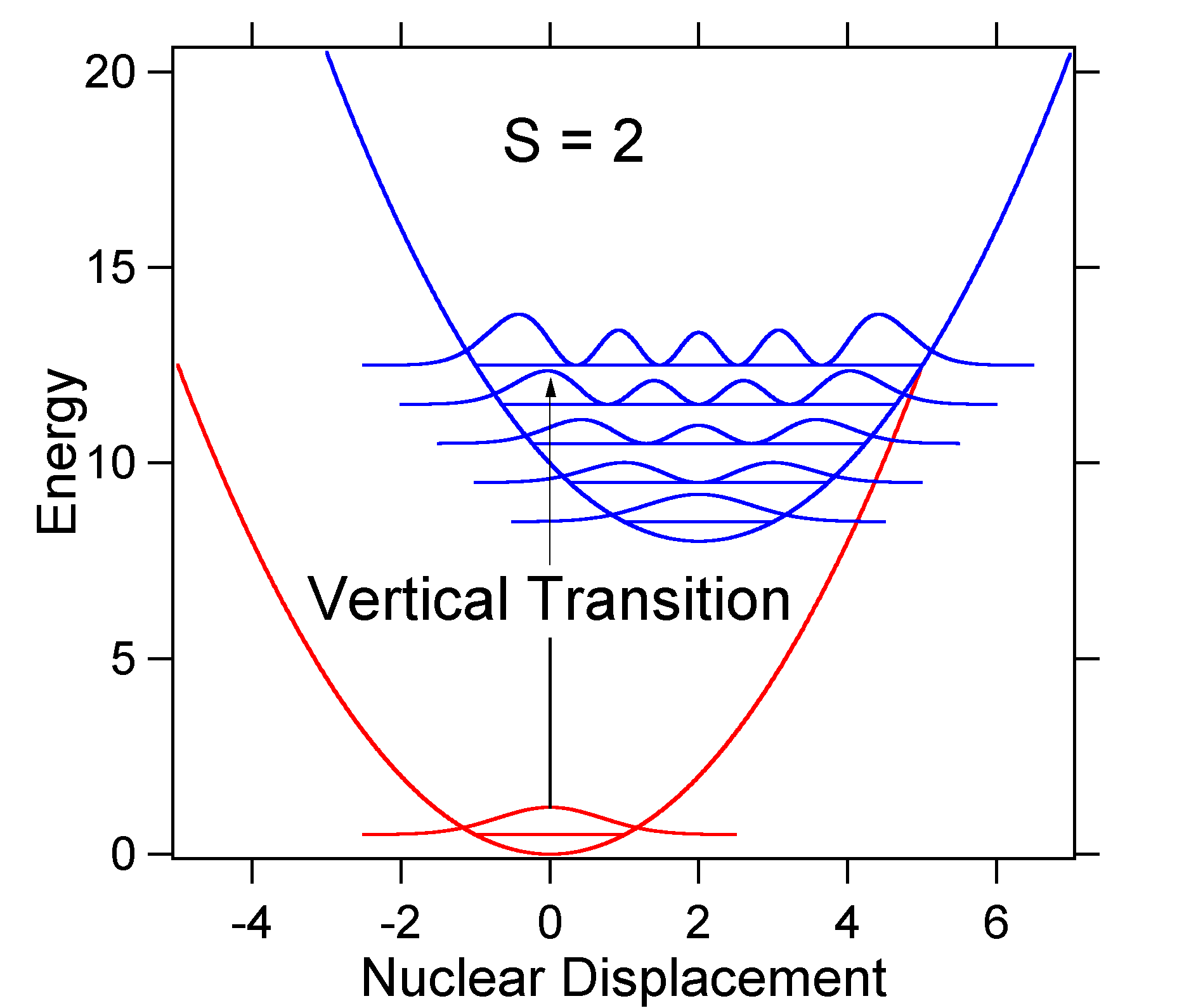
Die größere Verschiebung führt zu einer verringerten Überlappung des Grundzustandsniveaus mit dem v = 0-Niveau des angeregten Zustands. Die maximale Intensität wird in höheren Schwingungsniveaus erreicht, wie im Stockspektrum gezeigt.
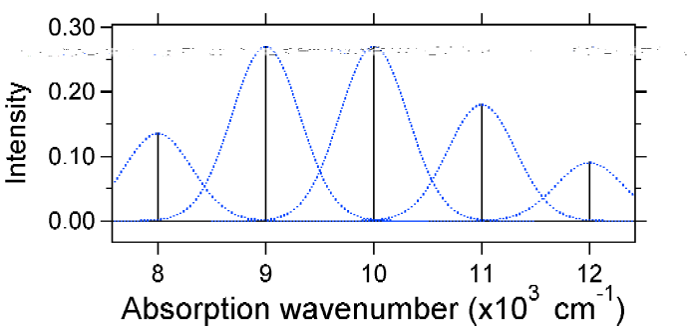
Die unten dargestellten Absorptionsspektren haben alle die gleiche integrierte Intensität, ihre Form ändert sich jedoch aufgrund des unterschiedlichen Ausmaßes der Verschiebung der potentiellen Energiefläche im angeregten Zustand.
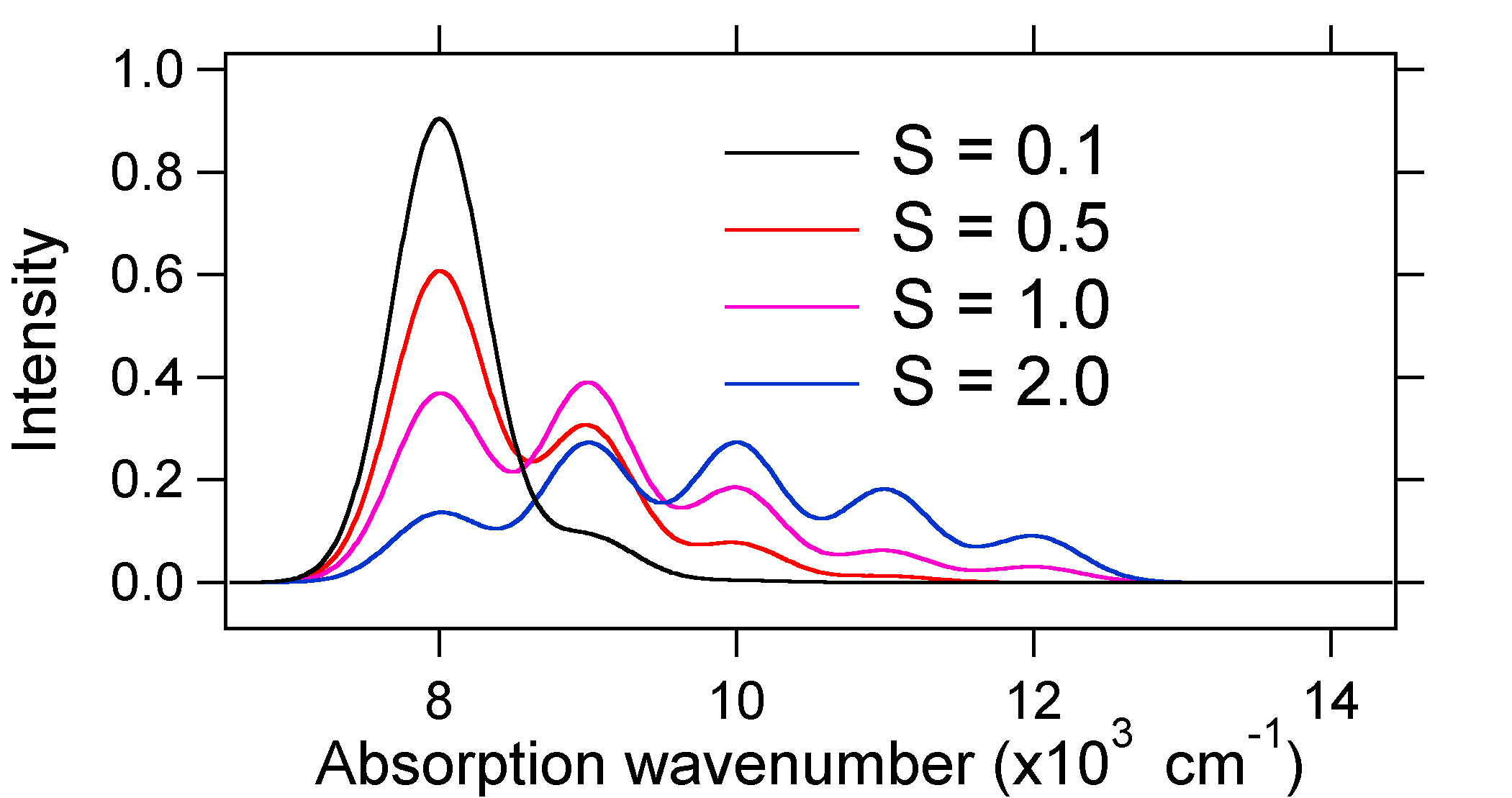
Die Art der relativen vibronischen Bandintensitäten kann uns also sagen, ob es eine Verschiebung der Gleichgewichtskernkoordinate gibt, die einen Übergang begleitet hat. Wann wird es eine Zunahme der Bindungslänge geben (dh \(Q_e > R_e\))? Dies tritt auf, wenn ein Elektron von einem Bindungsmolekülorbital zu einem nichtbindenden oder antibindenden Molekülorbital befördert wird (d. H. Wenn die Bindungsordnung im angeregten Zustand geringer ist als im Grundzustand).
- Nicht bindendes Molekülorbital \(\rightarrow\) bindendes Molekülorbital
- Anti-bindendes Molekülorbital \(\rightarrow\) bindendes Molekülorbital
- Anti-bindendes Molekülorbital \(\rightarrow\) nicht bindendes Molekülorbital
Kurz gesagt, wenn die Bindungsordnung im angeregten Zustand niedriger ist als im Grundzustand, dann \(Q_e > R_e\); In diesem Fall tritt eine Erhöhung der Bondlänge auf.In diesem Fall ist es wichtig, dass Sie sich an uns wenden. Ein anderer Ansatz zur Berechnung von Franck-Condon-Faktoren einschließlich Anharmonizität. In: J. Chem. Phys., 120 (2004), S. 813-822.
Contributors
- Matthe @ Ziering
-
Stefan Franzen (North Carolina State Universit