Deep Residual Networks verstehen

Deep Residual Networks (ResNet) eroberte die Deep Learning-Welt im Sturm, als Microsoft Research Deep Residual Learning für die Bilderkennung veröffentlichte. Diese Netzwerke führten zu 1st-Platz-Gewinnern in allen fünf Hauptstrecken der ImageNet- und COCO 2015-Wettbewerbe, die Bildklassifizierung, Objekterkennung und semantische Segmentierung abdeckten. Die Robustheit von ResNets wurde seitdem durch verschiedene visuelle Erkennungsaufgaben und durch nicht-visuelle Aufgaben mit Sprache und Sprache bewiesen. Ich habe ResNet auch zusätzlich zu anderen Deep-Learning-Modellen in meiner Dissertationsforschung verwendet.

Dieser Beitrag fasst die drei folgenden Artikel zusammen, die alle von Resnets Erfinder Kaiming He geschrieben oder mitgeschrieben wurden, da ich glaube, dass die Originalartikel die intuitivste und detaillierteste Erklärung des Modells / der Netzwerke geben. Hoffentlich könnte dieser Beitrag Ihnen helfen, den Kern von sozialen Netzwerken besser zu verstehen.

• Deep Residual Learning für die Bilderkennung
• Identity Mappings in Deep Residual Networks
• Aggregierte Residualtransformation für Deep Neural Networks

Intuition auf Deep Residual Network (Stackoverflow ref)

Ein Residual Block wird wie folgt angezeigt:

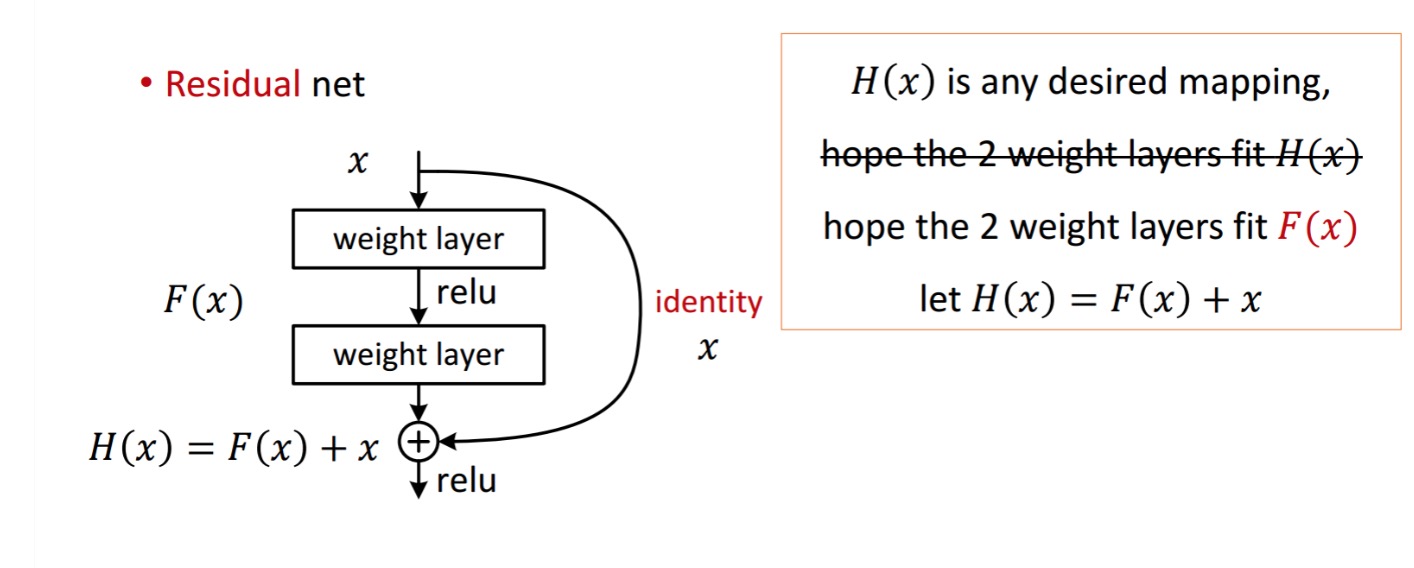
die gezeigte Resteinheit erhält man durch Verarbeitung mit zwei Gewichtsschichten. Dann fügt es hinzu, um zu erhalten . Angenommen, dies ist Ihre ideale vorhergesagte Ausgabe, die mit Ihrer Grundwahrheit übereinstimmt. Da das Erhalten des gewünschten davon abhängt, das Perfekte zu erhalten . Das bedeutet, dass die beiden Gewichtsschichten in der Resteinheit tatsächlich in der Lage sein sollten, das gewünschte zu erzeugen, dann ist das Erreichen des Ideals garantiert.

wird wie folgt erhalten.

wird wie folgt erhalten.

Die Autoren nehmen an, dass das restliche Mapping (dh ) möglicherweise einfacher zu optimieren ist als . Um mit einem einfachen Beispiel zu veranschaulichen, nehmen wir an, dass das Ideal . Für eine direkte Zuordnung wäre es dann schwierig, eine Identitätszuordnung zu erlernen, da es einen Stapel nichtlinearer Ebenen wie folgt gibt.

Es wäre also schwierig, die Identitätszuordnung mit all diesen Gewichtungen und ReLUs in der Mitte anzunähern.

Wenn wir nun das gewünschte Mapping definieren, brauchen wir nur get wie folgt.

Das oben Genannte zu erreichen ist einfach. Stellen Sie einfach ein beliebiges Gewicht auf Null und Sie erhalten eine Nullausgabe. Fügen Sie zurück und Sie erhalten Ihre gewünschte Zuordnung.

Deep Learning für die Bilderkennung

Problem

Wenn tiefere Netzwerke konvergieren, wurde ein Degradationsproblem aufgedeckt: Mit zunehmender Netzwerktiefe wird die Genauigkeit gesättigt und verschlechtert sich dann schnell.

Degradierung in Aktion sehen:

Nehmen wir ein flaches Netzwerk und sein tieferes Gegenstück, indem wir ihm mehr Ebenen hinzufügen.Worst-Case-Szenario: Die frühen Schichten eines tieferen Modells können durch ein flaches Netzwerk ersetzt werden, und die verbleibenden Schichten können nur als Identitätsfunktion fungieren (Eingabe gleich Ausgabe).

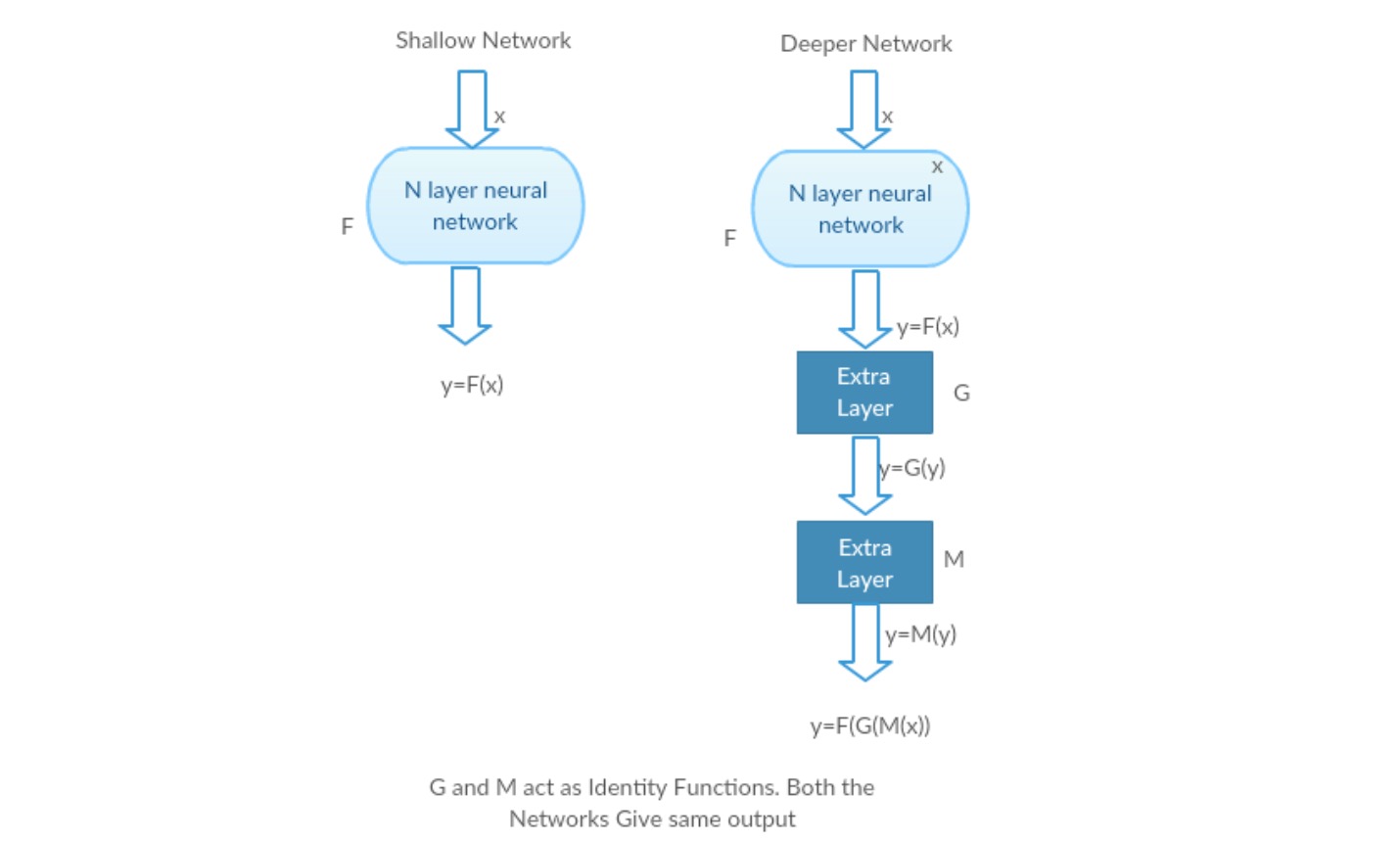
Lohnendes Szenario: Im tieferen Netzwerk nähern sich die zusätzlichen Schichten dem Mapping besser an als der flachere Gegenteil und reduzieren den Fehler erheblich.

Experiment: Im schlimmsten Fall sollten sowohl das flache Netzwerk als auch die tiefere Variante die gleiche Genauigkeit aufweisen. Im Belohnungsszenario sollte das tiefere Modell eine bessere Genauigkeit bieten als das flachere Gegenstück. Aber Experimente mit unseren gegenwärtigen Lösern zeigen, dass tiefere Modelle nicht gut funktionieren. Die Verwendung tieferer Netzwerke beeinträchtigt also die Leistung des Modells. Diese Arbeiten versuchen, dieses Problem mithilfe eines Deep-Learning-Frameworks zu lösen.

Wie zu lösen?

Anstatt eine direkte Abbildung von mit einer Funktion zu lernen (einige gestapelte nichtlineare Ebenen). Definieren wir die Restfunktion mit , die umformuliert werden kann , wobei und die gestapelten nichtlinearen Schichten bzw. die Identitätsfunktion (Eingabe = Ausgabe) darstellt.

Die Hypothese des Autors ist, dass es einfacher ist, die Restzuordnungsfunktion zu optimieren, als die ursprüngliche, nicht referenzierte Zuordnung zu optimieren .

Intuition hinter Restblöcken:

Nehmen wir das Identity Mapping als Beispiel (z.B. ). Wenn die Identitätszuordnung optimal ist, können wir die Residuen leicht auf Null setzen (), um eine Identitätszuordnung () durch einen Stapel nichtlinearer Schichten anzupassen. In einfacher Sprache ist es sehr einfach, eine Lösung zu finden, anstatt einen Stapel nichtlinearer CNN-Ebenen als Funktion zu verwenden (denken Sie darüber nach). Diese Funktion nannten die Autoren also Restfunktion.

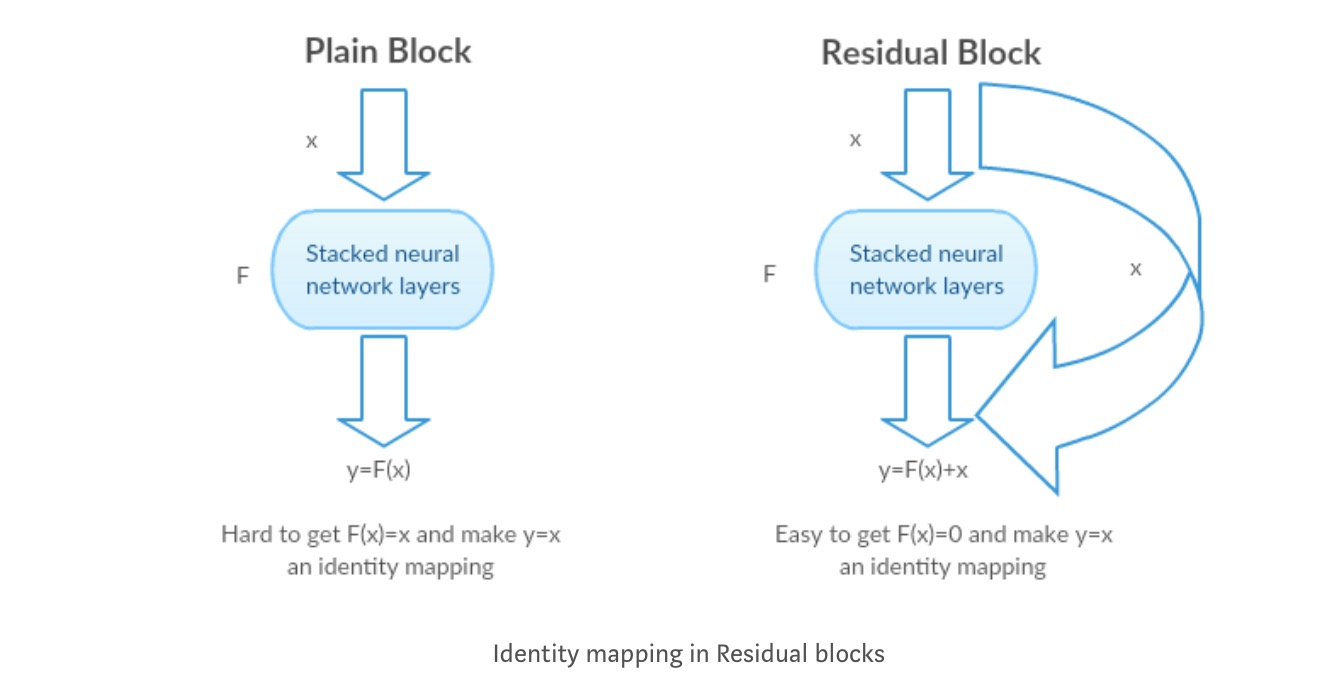
Die Autoren führten mehrere Tests durch, um ihre Hypothese zu testen. Schauen wir uns jetzt jeden von ihnen an.

Testfälle:

Nehmen Sie ein einfaches Netzwerk (VGG-18-Layer-Netzwerk) (Network-1) und eine tiefere Variante davon (34-Layer, Network-2) und fügen Sie dem Network-2 Restschichten hinzu (34-Layer mit Restverbindungen, Network-3).

Entwerfen des Netzwerks:

1. Verwenden Sie meistens 3 * 3 Filter.
2. Downsampling mit CNN-Schichten mit Stride 2.
3. Globale durchschnittliche Pooling-Schicht und am Ende eine 1000-Fach vollständig verbundene Schicht mit Softmax.

Es gibt zwei Arten von Restverbindungen:

I. Die Identity shortcuts () können direkt verwendet werden, wenn input () und output () die gleichen Abmessungen haben.

II. Wenn sich die Dimensionen ändern, A) Führt die Verknüpfung weiterhin eine Identitätszuordnung durch, wobei zusätzliche Nulleinträge mit der vergrößerten Dimension aufgefüllt werden. B) Die Projektionsverknüpfung wird verwendet, um die Dimension (durch 1 * 1 conv) unter Verwendung der folgenden Formel

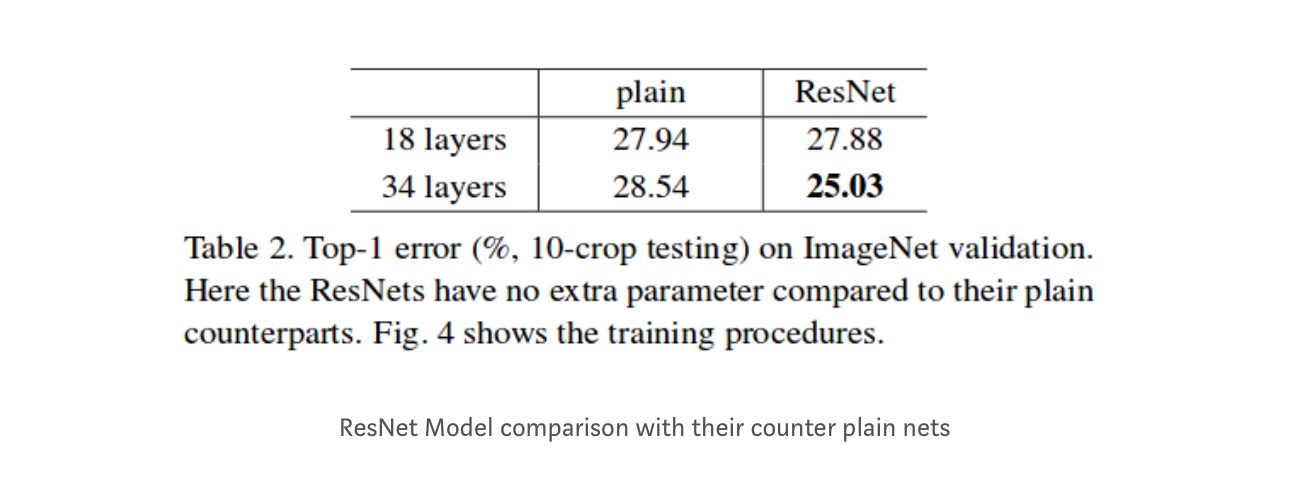
Ergebnisse

Obwohl das 18-Layer-Netzwerk nur der Unterraum im 34-Layer-Netzwerk ist, ist es immer noch besser. ResNet schneidet bei einem tieferen Netzwerk deutlich besser ab

Tiefere Studien

Darüber hinaus werden mehr Netzwerke untersucht:

Jeder ResNet-Block ist entweder 2-schichttief (Wird in kleinen Netzwerken wie ResNet 18, 34) oder 3 Schicht tief ( ResNet 50, 101, 152).

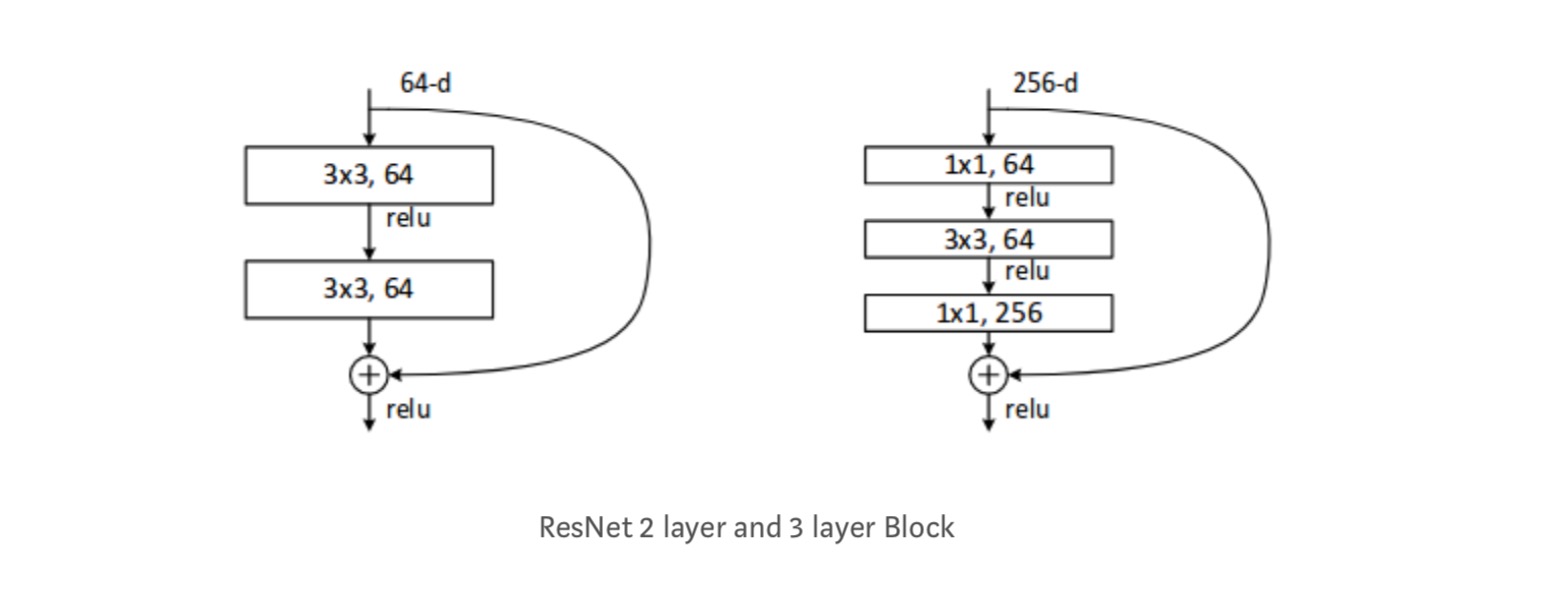
Beobachtungen

1. Das ResNet-Netzwerk konvergiert schneller als der einfache Gegenteil.
2. Identität vs. Shorcuts. Sehr kleine inkrementelle Gewinne mit Projektionsverknüpfungen (Gleichung-2) in allen Ebenen. Daher verwenden alle ResNet-Blöcke nur Identitätsverknüpfungen, wobei Projektionsverknüpfungen nur verwendet werden, wenn sich die Abmessungen ändern.ResNet-34 erreichte einen Top-5-Validierungsfehler von 5,71% besser als BN-3 und VGG. ResNet-152 erreicht einen Top-5-Validierungsfehler von 4,49%. Ein Ensemble von 6 Modellen mit unterschiedlichen Tiefen erreicht einen Top-5-Validierungsfehler von 3,57%. Gewinn des 1. Platzes in ILSVRC-2015

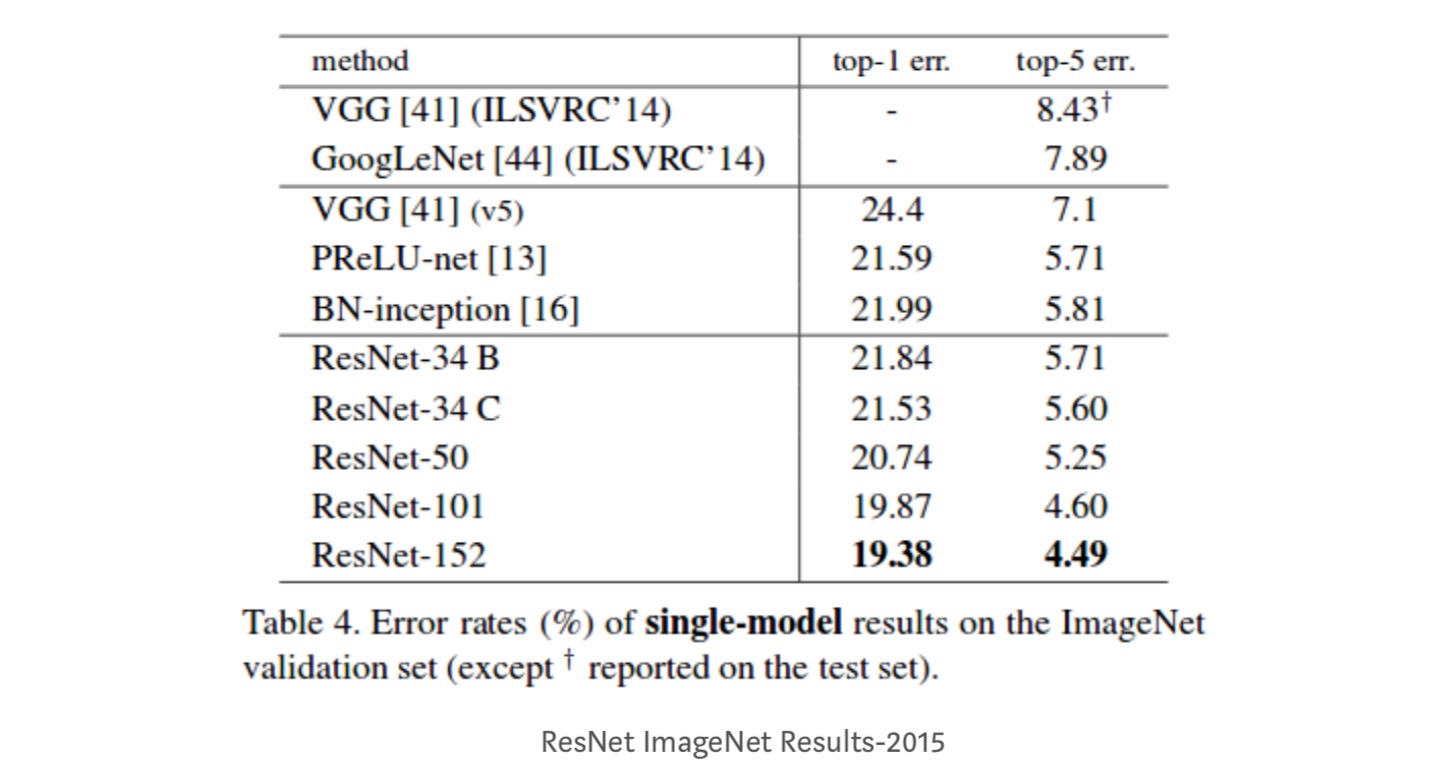
Identity Mappings in Deep Residual Networks

Dieser Beitrag vermittelt das theoretische Verständnis, warum das Problem des verschwindenden Gradienten in Residual Networks nicht vorhanden ist, und die Rolle von Skip-Verbindungen (Skip-Verbindungen bedeuten die Eingabe oder), indem Identity Mapping (x) durch verschiedene Funktionen ersetzt wird.

Einleitung

Tiefe Restnetzwerke bestehen aus vielen gestapelten „Resteinheiten“. Jede Einheit kann in einer allgemeinen Form ausgedrückt werden:

wobei und Eingabe und Ausgabe der Einheit sind und eine Restfunktion ist. Im letzten Papier, ist eine Identitätszuordnung und ist eine ReLU-Funktion.

Die zentrale Idee von ResNets ist es, die additive Restfunktion in Bezug auf zu lernen , mit der Schlüsselwahl, ein Identitätsmapping zu verwenden . Dies wird durch Anhängen einer Identity Skip-Verbindung („Verknüpfung“) realisiert.

In diesem Artikel analysieren wir tiefe Restnetzwerke, indem wir uns darauf konzentrieren, einen „direkten“ Pfad für die Verbreitung von Informationen zu schaffen — nicht nur innerhalb einer Resteinheit, sondern durch das gesamte Netzwerk. Unsere Ableitungen zeigen, dass, wenn beide und Identitätszuordnungen sind, Das Signal sowohl in Vorwärts- als auch in Rückwärtsgängen direkt von einer Einheit zu einer anderen Einheit propagiert werden kann. Unsere Experimente zeigen empirisch, dass das Training im Allgemeinen einfacher wird, wenn die Architektur näher an den beiden oben genannten Bedingungen liegt.

Um die Rolle von Skip-Verbindungen zu verstehen, analysieren und vergleichen wir verschiedene Arten von . Wir stellen fest, dass die im letzten Artikel gewählte Identitätszuordnung unter allen von uns untersuchten Varianten die schnellste Fehlerreduzierung und den niedrigsten Trainingsverlust erzielt, während die Verbindungen von Skalierung, Gating und 1 × 1-Faltungen alle zu höheren Trainingsverlusten und Fehlern führen. Diese Experimente legen nahe, dass ein „sauberer“ Informationspfad hilfreich ist, um die Optimierung zu erleichtern.

Um ein Identitätsmapping zu konstruieren, betrachten wir die Aktivierungsfunktionen (ReLU und BN) als „Voraktivierung“ der Gewichtsschichten, im Gegensatz zur herkömmlichen Weisheit der „Nachaktivierung“. Dieser Gesichtspunkt führt zu einer neuen Resteinheit Design, in der folgenden Abbildung dargestellt. Basierend auf dieser Einheit präsentieren wir wettbewerbsfähige Ergebnisse auf CIFAR-10/100 mit einem 1001-Layer-ResNet, das viel einfacher zu trainieren ist und besser verallgemeinert als das ursprüngliche ResNet. Wir berichten weiter über verbesserte Ergebnisse in ImageNet mit einem 200-Lagen-ResNet, für das das Gegenstück des letzten Papiers zu überpassen beginnt. Diese Ergebnisse legen nahe, dass es viel Raum gibt, die Dimension der Netzwerktiefe zu nutzen, ein Schlüssel zum Erfolg des modernen Deep Learning.

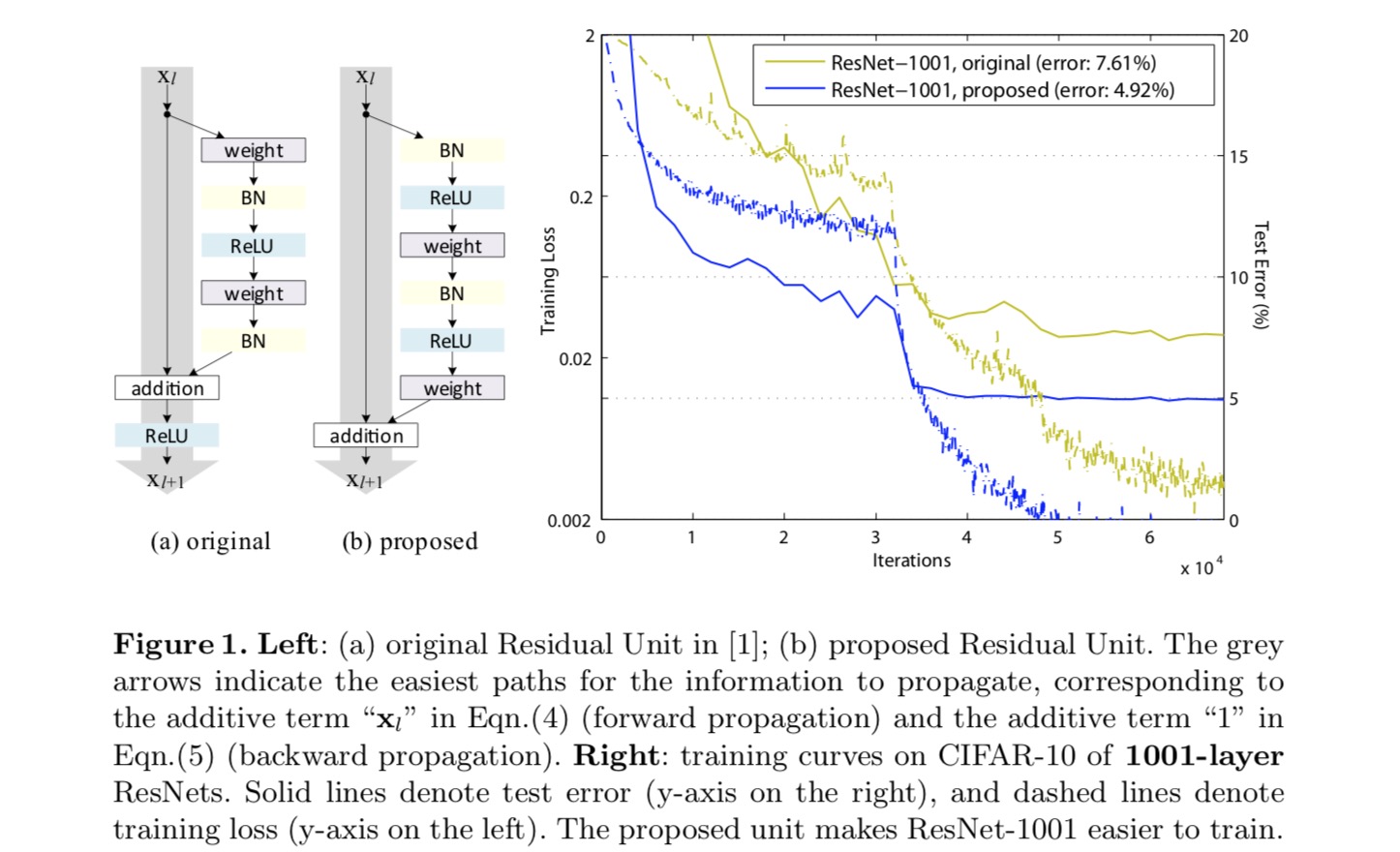
Analyse tiefer Restnetzwerke

Die im letzten Artikel entwickelten ResNets sind modularisierte Architekturen, die Bausteine derselben Verbindungsform stapeln. In diesem Papier nennen wir diese Blöcke „Resteinheiten“. Die ursprüngliche Resteinheit im letzten Papier führt die folgende Berechnung durch:

Hier ist das Eingabefeature für die -te Resteinheit. ist ein Satz von Gewichten (und Vorspannungen), die der -ten Resteinheit zugeordnet sind, und ist die Anzahl der Schichten in einer Resteinheit (ist 2 oder 3 im letzten Papier). bezeichnet die Restfunktion, e.g., ein Stapel von zwei 3 × 3 Faltungsschichten im letzten Papier. Die Funktion ist die Operation nach elementweiser Addition, und im letzten Papier ist ReLU. Die Funktion wird als Identitätszuordnung festgelegt: .

If ist auch eine Identitätszuordnung: , wir können erhalten:

Rekursiv haben wir:

für jede tiefere Einheit und jede flachere Einheit . Diese Gleichung zeigt einige schöneeigenschaften. (1) Das Merkmal einer tieferen Einheit kann als das Merkmal einer flacheren Einheit plus einer Restfunktion in Form von dargestellt werden , Dies zeigt an, dass sich das Modell in einer Restart zwischen beliebigen Einheiten befindet und . (2) Das Merkmal jeder Tiefeneinheit ist die Summation der Ausgänge aller vorhergehenden Restfunktionen (plus). Dies steht im Gegensatz zu einem „einfachen Netzwerk“, bei dem ein Merkmal beispielsweise eine Reihe von Matrix-Vektor-Produkten ist (wobei BN und ReLU ignoriert werden).

Die obige Gleichung führt auch zu schönen Rückwärtsausbreitungseigenschaften. Bezeichnen wir die Verlustfunktion als , aus der Kettenregel der Rückpropagation haben wir:

Die obige Gleichung zeigt an, dass der Gradient in zwei additive Terme zerlegt werden kann: ein Term davon propagiert Informationen direkt, ohne irgendwelche Gewichtsschichten zu betreffen, und ein anderer Term davon propagiert durch die Gewichtsschichten. Die obige Gleichung legt auch nahe, dass es unwahrscheinlich ist, dass der Gradient für eine Mini-Charge aufgehoben wird, da der Term im Allgemeinen nicht immer -1 für alle Proben in einer Mini-Charge sein kann. Dies bedeutet, dass der Gradient einer Schicht auch dann nicht verschwindet, wenn die Gewichte beliebig klein sind.

Die obigen zwei Gleichungen legen nahe, dass das Signal direkt von jeder Einheit zu einer anderen propagiert werden kann, sowohl vorwärts als auch rückwärts. Die Grundlage der ersten beiden obigen Gleichungen sind zwei Identitätszuordnungen: (1) die Identitätssprungverbindung und (2) die Bedingung, die eine Identitätszuordnung ist.

Bedeutung der Identität Verbindungen überspringen

Betrachten wir eine einfache Modifikation, , um die Identitätsknüpfung zu brechen:

wo ist ein modulierender Skalar (der Einfachheit halber nehmen wir immer noch Identität an). Wenn wir diese Formulierung rekursiv anwenden, erhalten wir eine Gleichung ähnlich der obigen:

wobei die Notation die Skalare in die Restfunktionen aufnimmt. In ähnlicher Weise haben wir eine Rückpropagation der folgenden Form:

Im Gegensatz zur vorherigen Gleichung wird in dieser Gleichung der erste additive Term um einen Faktor moduliert . Für ein extrem tiefes Netzwerk (ist groß), wenn für alle , kann dieser Faktor exponentiell groß sein; Wenn für alle , kann dieser Faktor exponentiell klein sein und verschwinden, was das rückpropagierte Signal von der Verknüpfung blockiert und es zwingt, durch die Gewichtsschichten zu fließen. Dies führt zu Optimierungsschwierigkeiten, wie wir durch Experimente zeigen.

In der obigen Analyse wird die ursprüngliche Identitätssprungverbindung durch eine einfache Skalierung ersetzt . Wenn die Skip-Verbindung kompliziertere Transformationen darstellt (wie Gating und 1×1-Faltungen), wird in der obigen Gleichung der erste Term where is the derivative of . Dieses Produkt kann auch die Informationsverbreitung behindern und den Trainingsprozess behindern, wie in den folgenden Experimenten gezeigt.

Experimente mit Skip-Verbindungen

Wir experimentieren mit dem 110-Layer ResNet auf CIFAR-10. Dieses extrem tiefe ResNet-110 hat 54 zweischichtige Resteinheiten (bestehend aus 3 × 3 Faltungsschichten) und ist eine Herausforderung für die Optimierung. Verschiedene Arten von Skip-Verbindungen werden experimentiert. Siehe folgende Abbildung:

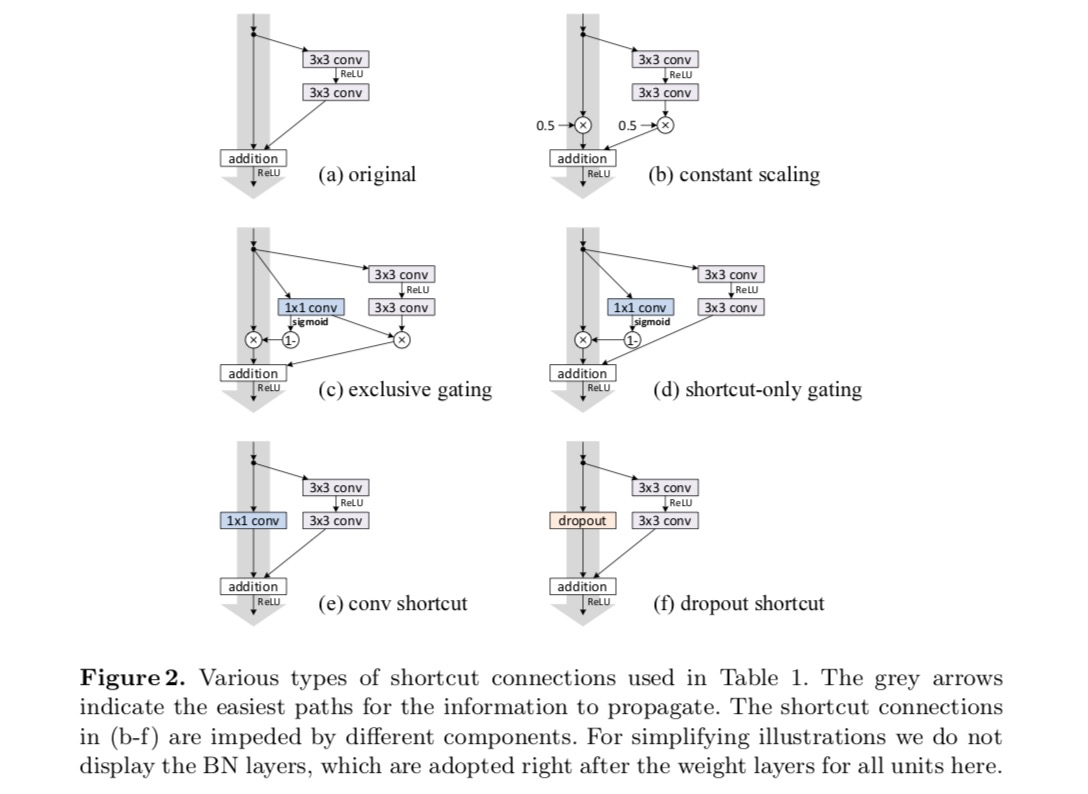
Die Klassifizierungsergebnisse werden in der folgenden Tabelle angezeigt:

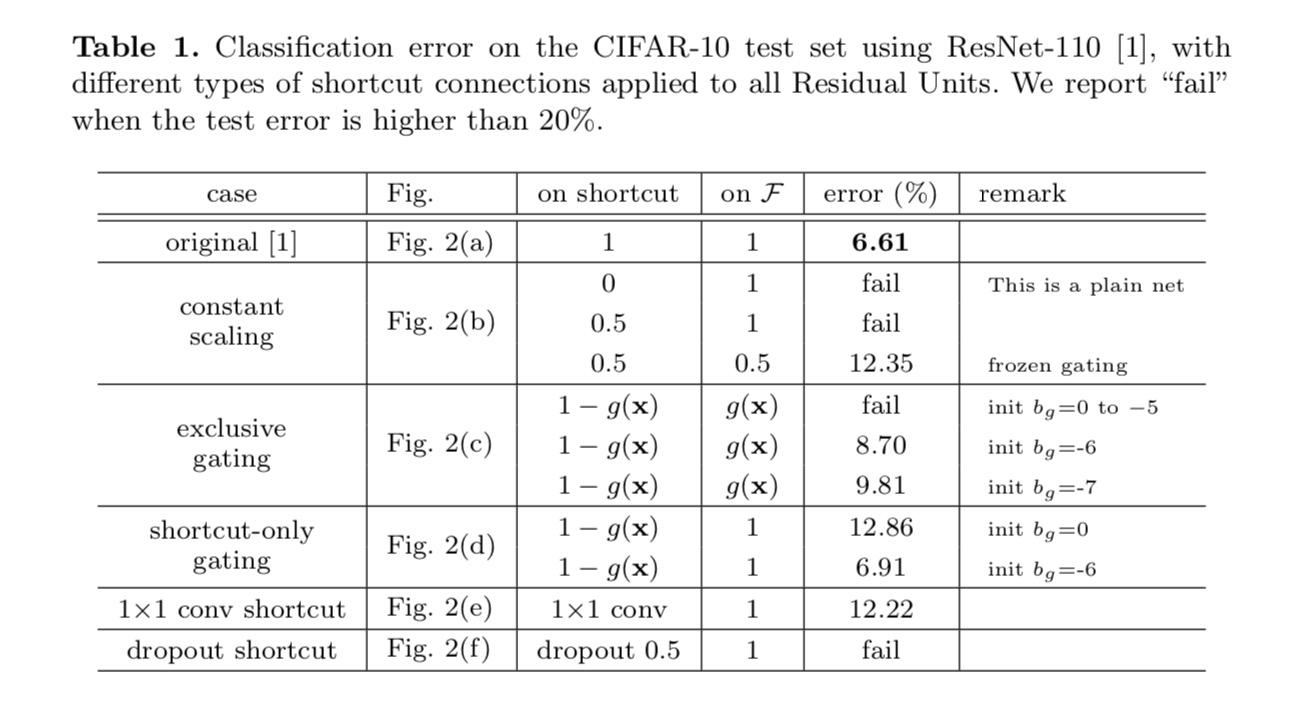
Wie durch die grauen Pfeile in der obigen Abbildung angedeutet, sind die Verknüpfungsverbindungen die direktesten Pfade für die Weitergabe der Informationen. Multiplikative Manipulationen (Skalierung, Gating, 1 × 1-Faltungen und Dropout) auf den Verknüpfungen können die Informationsausbreitung behindern und zu Optimierungsproblemen führen.

Es ist bemerkenswert, dass die Gating- und 1 × 1-Faltungsverknüpfungen mehr Parameter einführen und stärkere Repräsentationsfähigkeiten als Identitätsknüpfungen haben sollten. Tatsächlich decken das Gating nur für Verknüpfungen und die 1 × 1-Faltung den Lösungsraum von Identitätsverknüpfungen ab (dh sie könnten als Identitätsverknüpfungen optimiert werden). Ihr Trainingsfehler ist jedoch höher als der von Identitätsmodellen, was darauf hinweist, dass die Verschlechterung dieser Modelle durch Optimierungsprobleme anstelle von Darstellungsfähigkeiten verursacht wird.

Verwendung von Aktivierungsfunktionen

Experimente im obigen Abschnitt gehen davon aus, dass die Aktivierung nach der Addition die Identitätszuordnung ist. Aber in den obigen Experimenten ist ReLU wie in dem ersten Papier entworfen. Als nächstes untersuchen wir die Auswirkungen von .

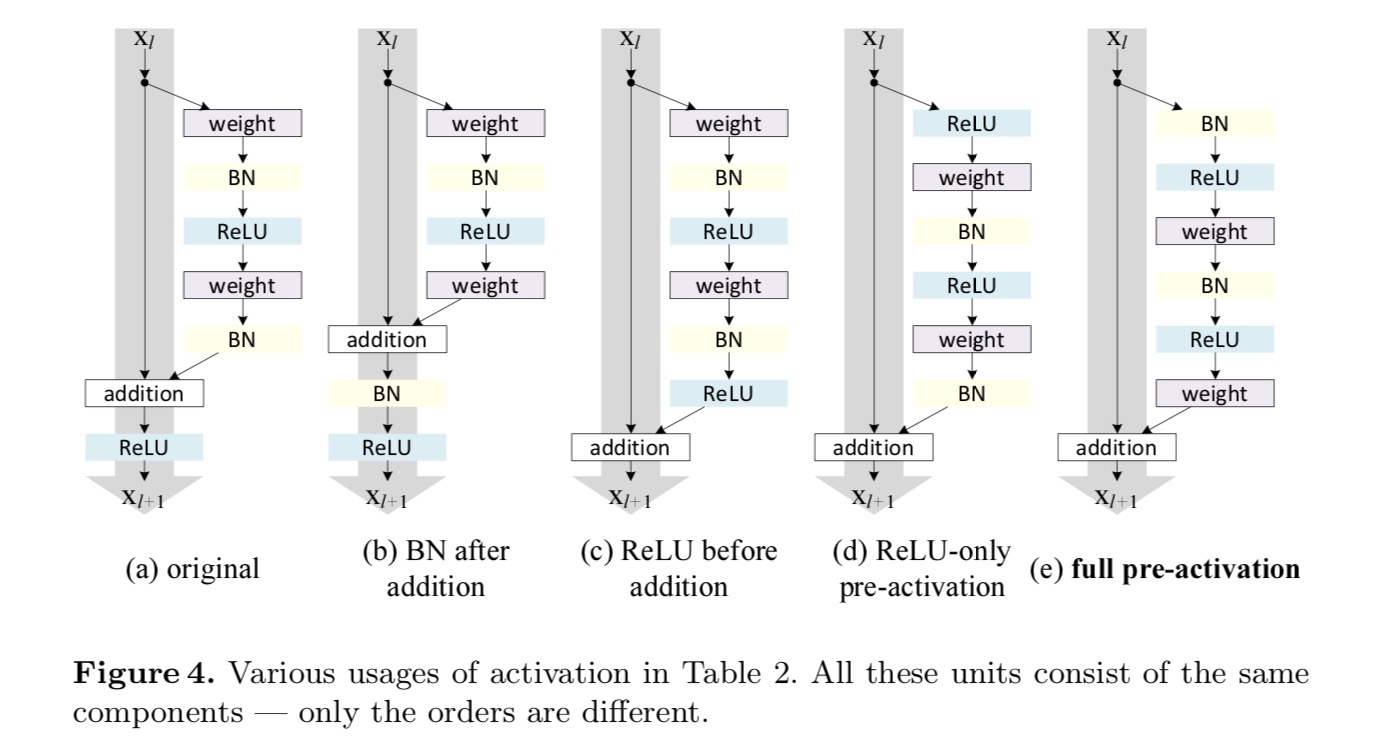
Wir möchten eine Identitätszuordnung vornehmen, die durch Neuanordnung der Aktivierungsfunktionen (ReLU und / oder BN, Batch-Normalisierung) erfolgt. In der folgenden Abbildung hat die ursprüngliche Resteinheit im letzten Papier eine Form in Fig. 4(a) – BN wird nach jeder Gewichtsschicht verwendet, und ReLU wird nach BN übernommen, mit der Ausnahme, dass das letzte ReLU in einer Resteinheit nach elementweiser Addition (= ReLU) erfolgt. Abb. 4(b-e) zeigen die von uns untersuchten Alternativen.

Experimente zur Aktivierung

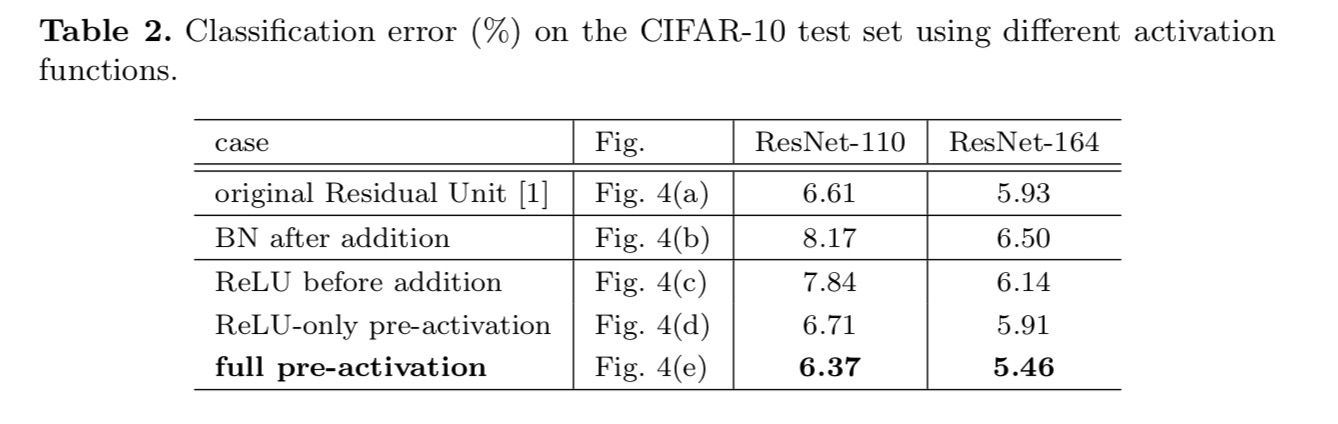
In diesem Abschnitt experimentieren wir mit ResNet-110 und einer 164-Layer-Bottleneck-Architektur (bezeichnet als ResNet-164). Eine Engpass-Resteinheit besteht aus einer 1 × 1-Schicht zum Reduzieren der Dimension, einer 3 × 3-Schicht und einer 1 × 1-Schicht zum Wiederherstellen der Dimension. Wie im letzten Artikel beschrieben, ähnelt seine Rechenkomplexität der Zwei-3 × 3-Resteinheit.

Nachaktivierung oder Voraktivierung?

Im ursprünglichen Entwurf wirkt sich die Aktivierung auf beide Pfade in der nächsten Resteinheit aus: . Als nächstes entwickeln wir eine asymmetrische Form, bei der eine Aktivierung nur den Pfad betrifft: , für alle . Durch Umbenennen der Notationen haben wir die folgende Form:

Für diese neue Resteinheit wie in der obigen Gleichung wird die neue Nachadditionsaktivierung zu einer Identitätszuordnung. Diese Ausgestaltung bedeutet, dass, wenn eine neue Nachaktivierung asymmetrisch übernommen wird, diese einer Neucastierung als Voraktivierung der nächsten Resteinheit gleichkommt. Dies ist in der folgenden Abbildung dargestellt:

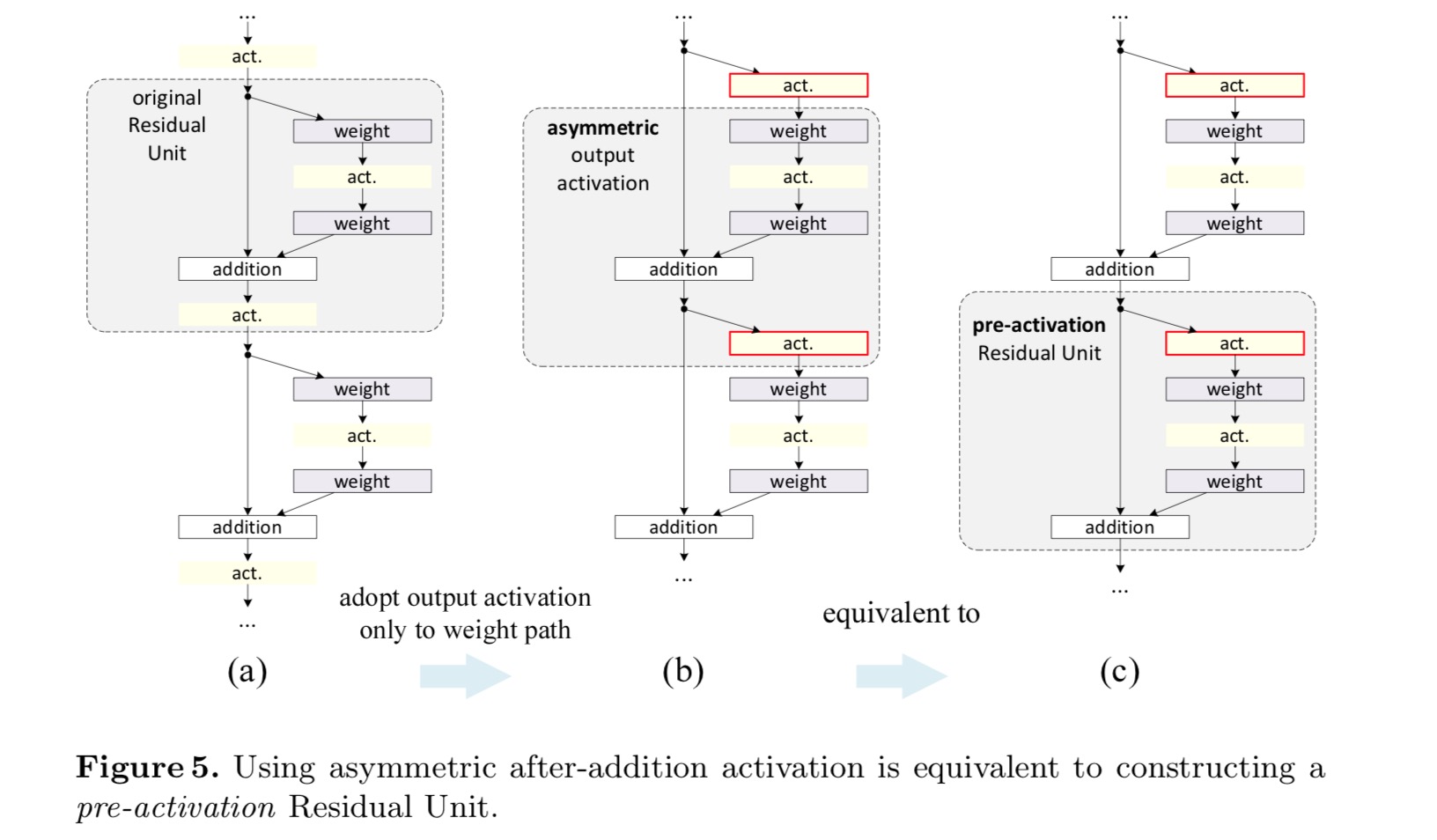
Die Unterscheidung zwischen Post-Aktivierung/Pre-Aktivierung wird durch das Vorhandensein der elementweisen Addition verursacht. Für ein einfaches Netzwerk mit N Schichten gibt es N − 1-Aktivierungen (BN / ReLU), und es spielt keine Rolle, ob wir sie als Post- oder Präaktivierungen betrachten. Aber für verzweigte Schichten, die durch Addition zusammengeführt werden, ist die Position der Aktivierung wichtig. Die verschiedenen Verwendungen der Aktivierung sind in Abbildung 4 dargestellt.

Wir experimentieren mit zwei solchen Designs: (1) ReLU-nur Voraktivierung und (2) vollständige Voraktivierung, wobei BN und ReLU beide vor Gewichtsschichten übernommen werden. Irgendwie überraschend, wenn BN und ReLU beide als Voraktivierung verwendet werden, werden die Ergebnisse durch gesunde Margen verbessert

Wir finden, dass die Auswirkungen der Voraktivierung zweifach sind. Erstens wird die Optimierung weiter vereinfacht (im Vergleich zum Baseline-ResNet), da es sich bei f um ein Identitätsmapping handelt. Zweitens verbessert die Verwendung von BN als Voraktivierung die Regularisierung der Modelle.

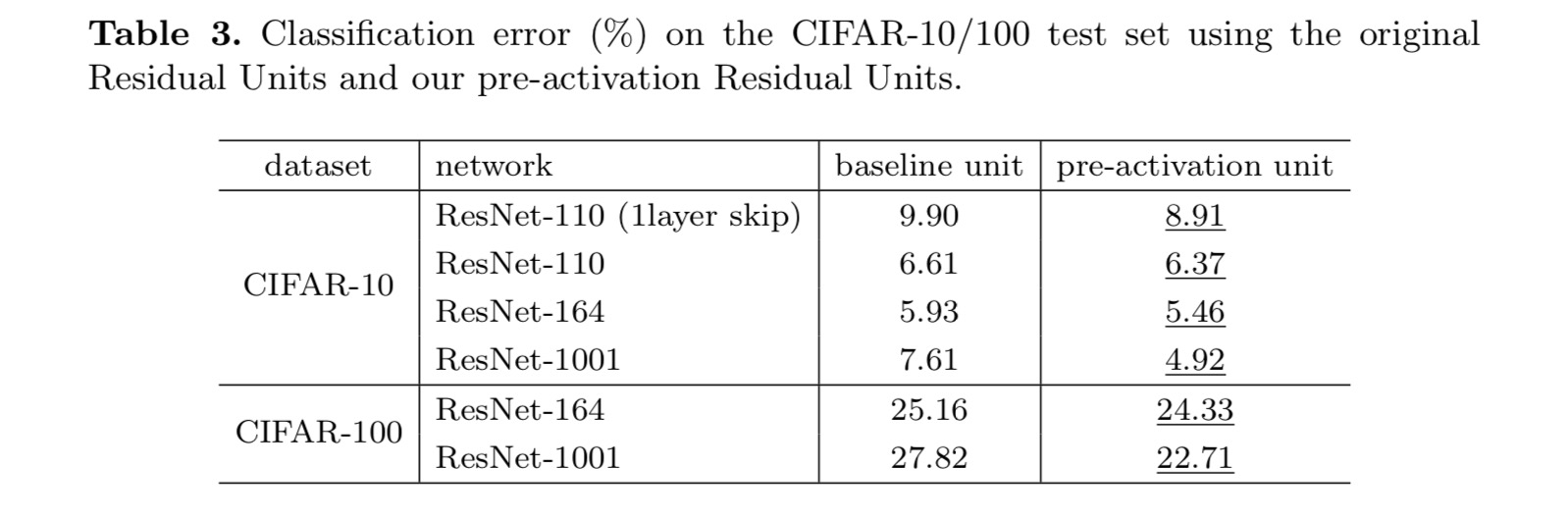
Fazit

Dieser Beitrag untersucht die Ausbreitungsformulierungen hinter den Verbindungsmechanismen tiefer Restnetzwerke. Unsere Ableitungen implizieren, dass Identitätsverkürzungsverbindungen und Identitätsnachadditionsaktivierung für eine reibungslose Informationsverbreitung unerlässlich sind. Ablationsexperimente zeigen Phänomene, die mit unseren Ableitungen übereinstimmen. Wir präsentieren auch tiefe 1000-Layer-Netzwerke, die leicht trainiert werden können und eine verbesserte Genauigkeit erzielen.

Aggregierte Residualtransformation für tiefe neuronale Netze

Einleitung

Die Forschung zur visuellen Erkennung befindet sich in einem Übergang vom „Feature Engineering“ zum „Network Engineering“. Die menschlichen Anstrengungen wurden auf die Entwicklung besserer Netzwerkarchitekturen für Lernrepräsentationen verlagert.

Das Entwerfen von Architekturen wird mit der wachsenden Anzahl von Hyper-Parametern immer schwieriger, insbesondere wenn es viele Ebenen gibt. Die VGG-Netze zeigen eine einfache, aber effektive Strategie zum Aufbau sehr tiefer Netzwerke: das Stapeln von Bausteinen gleicher Form. Diese Strategie wird von ResNets geerbt, die Module derselben Topologie stapeln. Diese einfache Regel reduziert die freie Auswahl von Hyperparametern, und die Tiefe wird als wesentliche Dimension in neuronalen Netzen offengelegt. Darüber hinaus argumentieren wir, dass die Einfachheit dieser Regel das Risiko einer übermäßigen Anpassung der Hyperparameter an einen bestimmten Datensatz verringern kann. Die Robustheit von VGG-Netzen und ResNets wurde durch verschiedene visuelle Erkennungsaufgaben und durch nicht-visuelle Aufgaben mit Sprache und Sprache bewiesen.

Im Gegensatz zu VGG-Netzen hat die Familie der Inception-Modelle gezeigt, dass sorgfältig entworfene Topologien in der Lage sind, eine überzeugende Genauigkeit bei geringer theoretischer Komplexität zu erreichen. Die Inception-Modelle haben sich im Laufe der Zeit weiterentwickelt, aber eine wichtige gemeinsame Eigenschaft ist eine Split-Transform-Merge-Strategie. In einem Inception-Modul wird die Eingabe in einige niederdimensionale Einbettungen (durch 1 × 1-Faltungen) aufgeteilt, die durch einen Satz spezialisierter Filter (3 × 3, 5 × 5 usw.) transformiert werden.), und durch Verkettung zusammengeführt. Es wird erwartet, dass sich das Split-Transform-Merge-Verhalten dieser Module der Darstellungskraft großer und dichter Schichten nähert, jedoch mit einer erheblich geringeren Rechenkomplexität.

Trotz guter Genauigkeit war die Realisierung von Inception-Modellen mit einer Reihe komplizierter Faktoren verbunden. Obwohl sorgfältige Kombinationen dieser Komponenten hervorragende neuronale Netzwerkrezepte ergeben, ist es im Allgemeinen unklar, wie die Inception-Architekturen an neue Datensätze / Aufgaben angepasst werden können, insbesondere wenn viele Faktoren und Hyper-Parameter entworfen werden müssen.

In diesem Beitrag stellen wir eine einfache Architektur vor, die die Strategie von VGG / ResNets übernimmt, Ebenen zu wiederholen, während die Split-Transform-Merge-Strategie auf einfache und erweiterbare Weise ausgenutzt wird. Ein Modul in unserem Netzwerk führt eine Reihe von Transformationen durch, jede auf einer niedrigdimensionalen Einbettung, deren Ausgaben durch Summation aggregiert werden. Wir verfolgen eine einfache Realisierung dieser Idee — die zu aggregierenden Transformationen haben alle dieselbe Topologie. Dieses Design ermöglicht es uns, auf eine große Anzahl von Transformationen ohne spezielle Designs zu erweitern.

Wir zeigen empirisch, dass unsere aggregierten Transformationen das ursprüngliche ResNet-Modul übertreffen, selbst unter der eingeschränkten Bedingung, die Rechenkomplexität und Modellgröße beizubehalten. Wir betonen, dass es zwar relativ einfach ist, die Genauigkeit durch Erhöhung der Kapazität (tiefer oder breiter) zu erhöhen, Methoden, die die Genauigkeit erhöhen und gleichzeitig die Komplexität beibehalten (oder verringern), in der Literatur jedoch selten sind.

Unsere Methode zeigt, dass die Kardinalität (die Größe der Menge der Transformationen) eine konkrete, messbare Dimension ist, die neben den Dimensionen Breite und Tiefe von zentraler Bedeutung ist. Experimente zeigen, dass die Erhöhung der Kardinalität ein effektiverer Weg ist, um Genauigkeit zu erlangen, als tiefer oder breiter zu gehen, insbesondere wenn Tiefe und Breite für bestehende Modelle abnehmende Erträge bringen.

Unsere neuronalen Netze mit dem Namen ResNeXt (was auf die nächste Dimension hindeutet) übertreffen ResNet-101/152, ResNet-200, Inception-v3 und Inception-ResNet-v2 im ImageNet-Klassifizierungsdatensatz. Insbesondere ein ResNeXt mit 101 Schichten kann eine bessere Genauigkeit als ResNet-200 erreichen, weist jedoch nur eine Komplexität von 50% auf. Darüber hinaus weist ResNeXt wesentlich einfachere Designs auf als alle anderen Modelle.

Methode

Wir verwenden ein stark modularisiertes Design nach VGG/ResNets. Unser Netzwerk besteht aus einem Stapel von Restblöcken. Diese Blöcke haben die gleiche Topologie und unterliegen zwei einfachen Regeln, die von VGG / ResNets inspiriert sind: (1) Wenn räumliche Karten derselben Größe erstellt werden, haben die Blöcke dieselben Hyperparameter (Breite und Filtergröße), und (2) Jedes Mal, wenn die räumliche Karte um den Faktor 2 heruntergesampelt wird, wird die Breite der Blöcke mit dem Faktor 2 multipliziert. Die zweite Regel stellt sicher, dass die Rechenkomplexität in Bezug auf FLOPs (Gleitkommaoperationen, in Anzahl der Multiplikationsadditionen) für alle Blöcke ungefähr gleich ist.

Mit diesen beiden Regeln müssen wir nur ein Template-Modul entwerfen, und alle Module in einem Netzwerk können entsprechend bestimmt werden. Diese beiden Regeln schränken den Gestaltungsraum stark ein und ermöglichen es uns, uns auf einige Schlüsselfaktoren zu konzentrieren. Die nach diesen Regeln erstellten Netzwerke sind in Tabelle 1 aufgeführt.

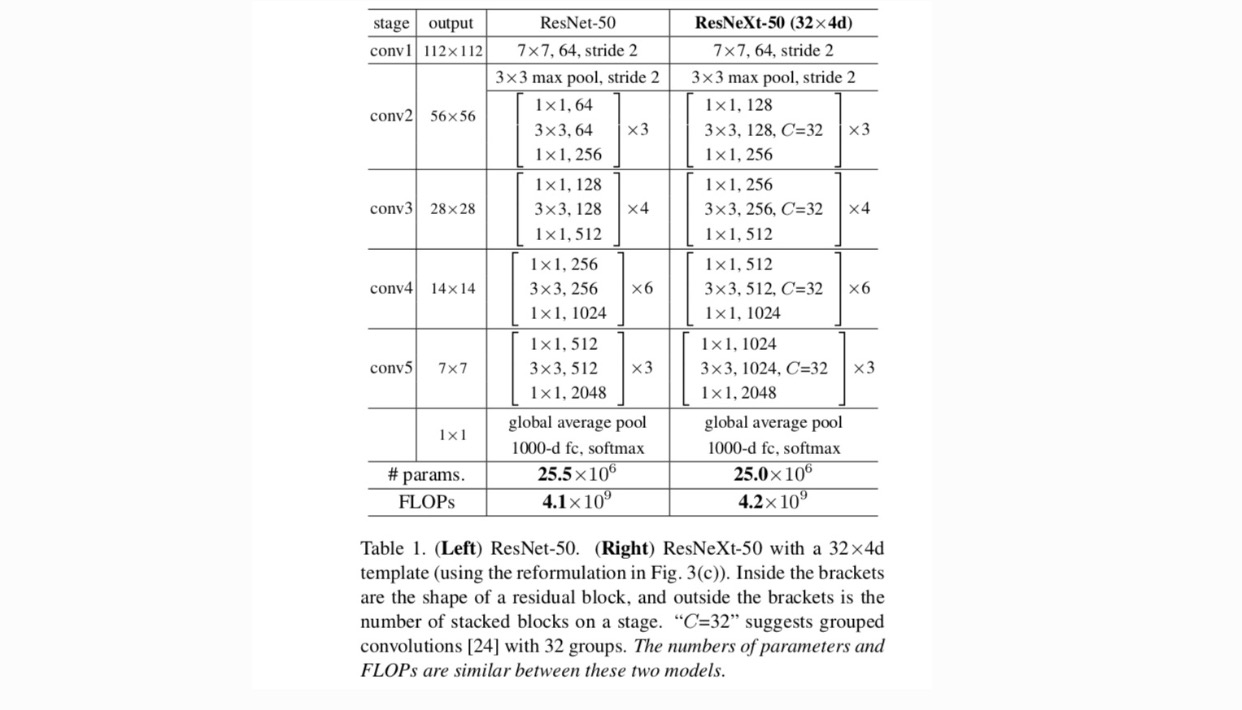
Die einfachsten Neuronen in künstlichen neuronalen Netzen führen ein inneres Produkt (gewichtete Summe) durch, dh die elementare Transformation, die durch vollständig verbundene und Faltungsschichten durchgeführt wird.

Die obige Operation kann als eine Kombination aus Teilen, Transformieren und Aggregieren neu gefasst werden. (1): Teilen: Der Vektor wird als niedrigdimensionale Einbettung geschnitten und im obigen Fall ist es ein eindimensionaler Unterraum (2) Transformieren: Die niedrigdimensionale Darstellung wird transformiert und im obigen Fall wird sie einfach skaliert: (3) Aggregieren: Die Transformationen in allen Einbettungen werden durch aggregiert .

Angesichts der obigen Analyse eines einfachen Neurons erwägen wir, die Elementartransformation (w_i, x_i) durch eine allgemeinere Funktion zu ersetzen, die an sich auch ein Netzwerk sein kann. Formal präsentieren wir aggregierte Transformationen als:

wobei eine beliebige Funktion sein kann. Analog zu einem einfachen Neuron, in eine (gegebenenfalls niedrigdimensionale) Einbettung projizieren und dann transformieren.

Wir sprechen von Kardinalität. ist in einer ähnlichen Position wie in , muss aber nicht gleich sein und kann eine beliebige Zahl sein. Wir zeigen durch Experimente, dass Kardinalität eine wesentliche Dimension ist und effektiver sein kann als die Dimensionen Breite und Tiefe.

In diesem Artikel betrachten wir eine einfache Möglichkeit, die Transformationsfunktionen zu entwerfen: Alle haben die gleiche Topologie. Dies erweitert die Strategie im VGG-Stil, Ebenen derselben Form zu wiederholen. Wir setzen die individuelle Transformation auf die in Abb. 1 (rechts). In diesem Fall erzeugt jeweils die erste 1×1-Schicht die niedrigdimensionale Einbettung.

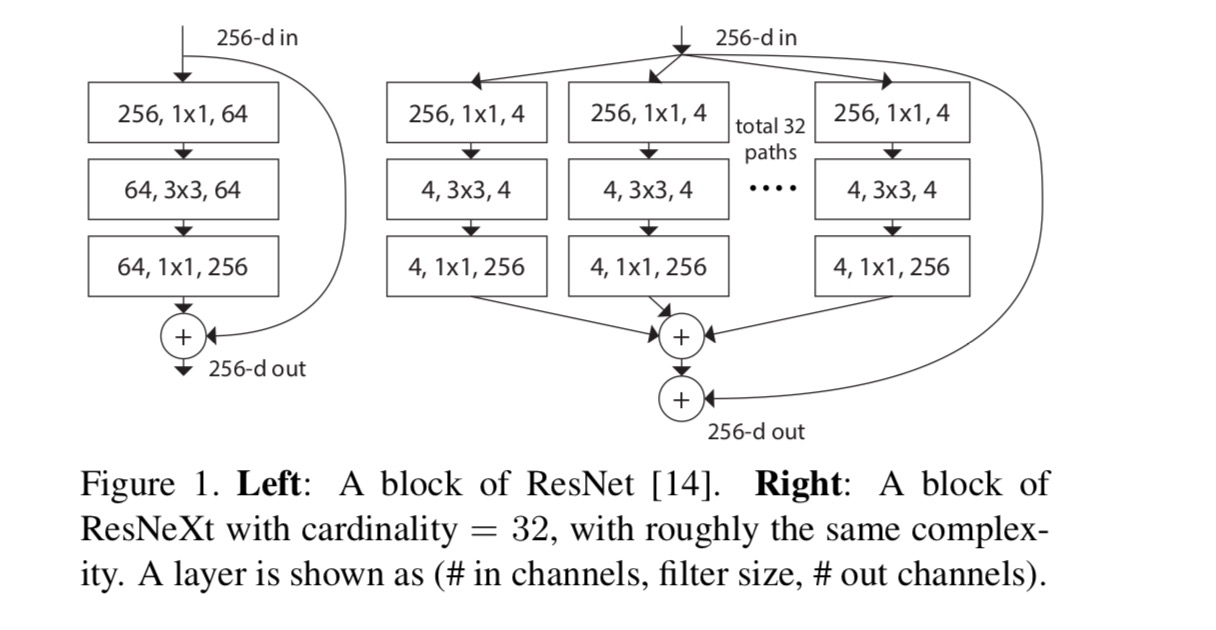
Die aggregierte Transformation in der letzten Gleichung dient als Restfunktion:

Wo ist die Ausgabe.

Die Beziehungen zwischen ResNeXt und Inception-ResNet/Grouped-Convolutions sind in der folgenden Abbildung dargestellt:

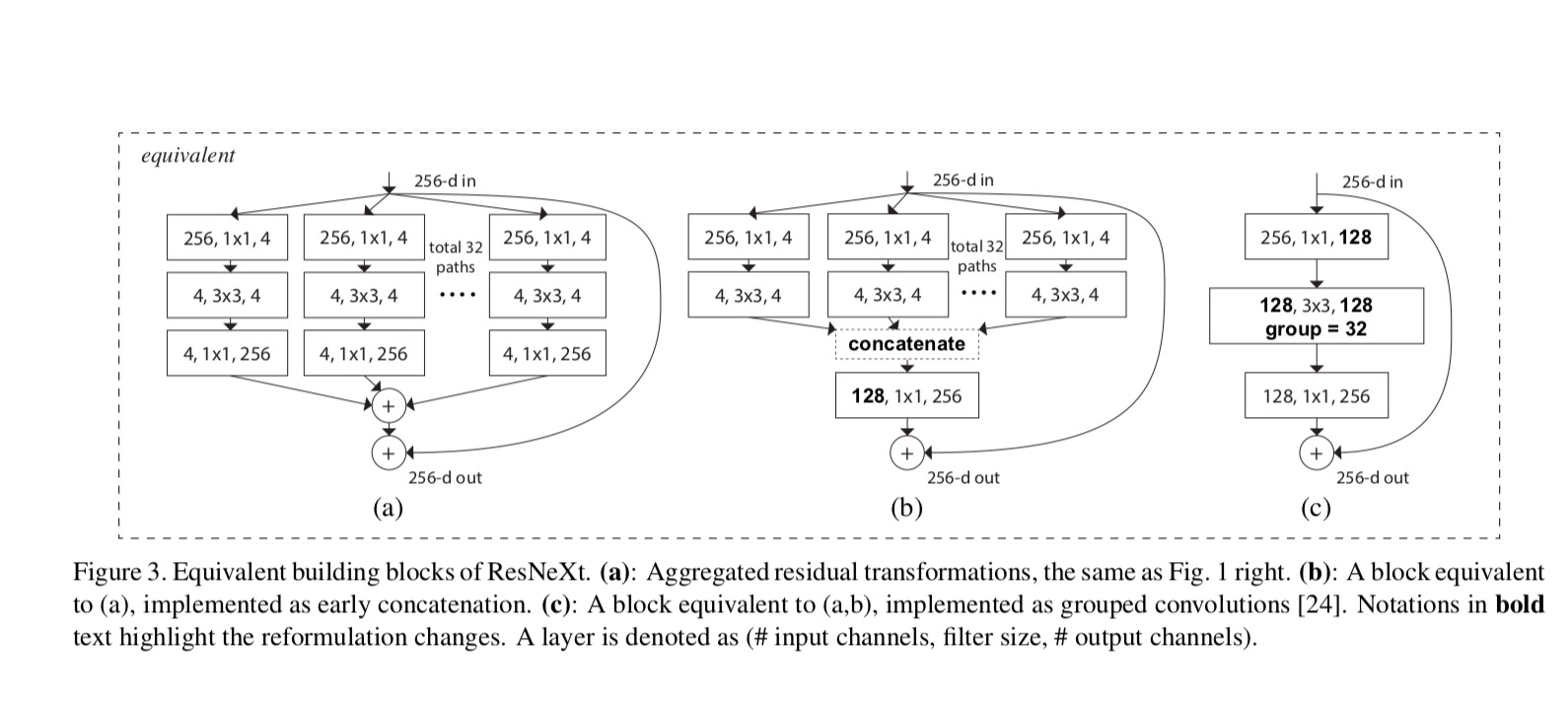
Wenn wir verschiedene Kardinalitäten unter Beibehaltung der Komplexität bewerten, möchten wir die Änderung anderer Hyper-Parameter minimieren. Wir entscheiden uns, die Breite des Engpasses anzupassen (z. B. 4-d in Abb. 1 (rechts)), da er vom Eingang und Ausgang des Blocks isoliert werden kann. Diese Strategie führt keine Änderung an anderen Hyperparametern (Tiefe oder Eingabe- / Ausgabebreite von Blöcken) ein und ist daher hilfreich, um uns auf die Auswirkungen der Kardinalität zu konzentrieren.

In Fig. 1 (links) hat der ursprüngliche ResNet-Engpassblock Parameter und proportionale FLOPs (auf derselben Feature-Map-Größe). Bei Engpassbreite zeigt unsere Schablone in Abb. 1(rechts) hat: Parameter und proportionale FLOPs. Wann und , diese Nummer . Die folgende Tabelle zeigt die Beziehung zwischen Kardinalität und Engpassbreite .

Experimente

Kardinalität vs. Breite. Wir bewerten zunächst den Kompromiss zwischen Kardinalität und Engpassbreite unter Berücksichtigung der Komplexität, wie in Tabelle 2 aufgeführt. Tabelle 3 zeigt die Ergebnisse. Im Vergleich zu ResNet-50 weist das 32 × 4d ResNeXt-50 einen Validierungsfehler von 22,2% auf, was 1,7% niedriger ist als die 23,9% der ResNet-Baseline. Da die Kardinalität von 1 auf 32 steigt und gleichzeitig die Komplexität erhalten bleibt, nimmt die Fehlerrate weiter ab. Darüber hinaus hat der 32 × 4d ResNeXt auch einen viel geringeren Trainingsfehler als der ResNet countetpart, was darauf hindeutet, dass die Gewinne nicht aus der Regularisierung, sondern aus stärkeren Darstellungen stammen.

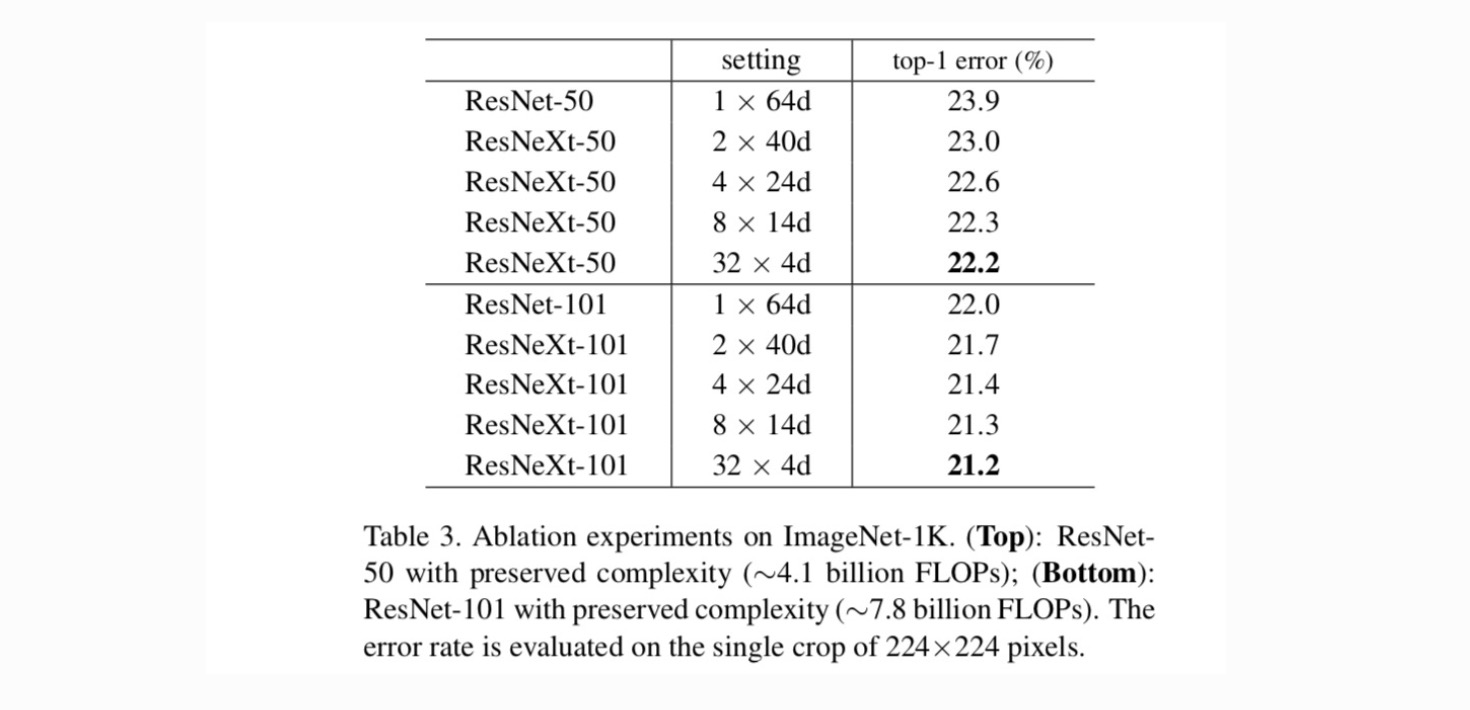
Zunehmende Kardinalität vs. Tiefer /Breiter.

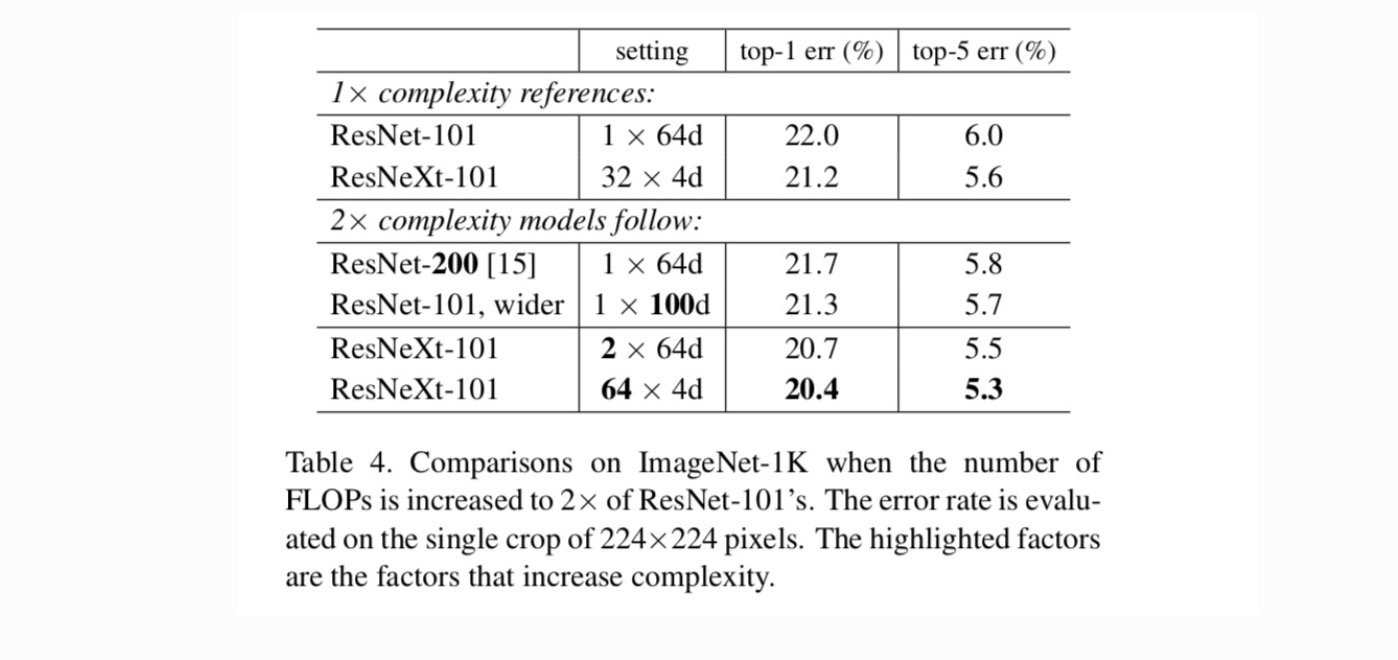
Als nächstes untersuchen wir die zunehmende Komplexität durch Erhöhung der Kardinalität C oder Erhöhung der Tiefe oder Breite. Wir vergleichen die folgenden Varianten (1), die tiefer zu 200 Schichten gehen. Wir nehmen das ResNet-200 an. (2) Gehen Sie breiter, indem Sie die Engpassbreite erhöhen. (3) Erhöhung der Kardinalität durch Verdoppelung von C.

Tabelle 4 zeigt, dass eine Erhöhung der Komplexität um 2 × den Fehler gegenüber der ResNet-101-Baseline (22,0%) konsistent reduziert. Die Verbesserung ist jedoch gering, wenn sie tiefer (ResNet-200 um 0, 3%) oder breiter (breiteres ResNet-101 um 0, 7%) geht. Im Gegenteil, zunehmende Kardinalität C zeigt viel bessere Ergebnisse als tiefer oder breiter zu gehen.

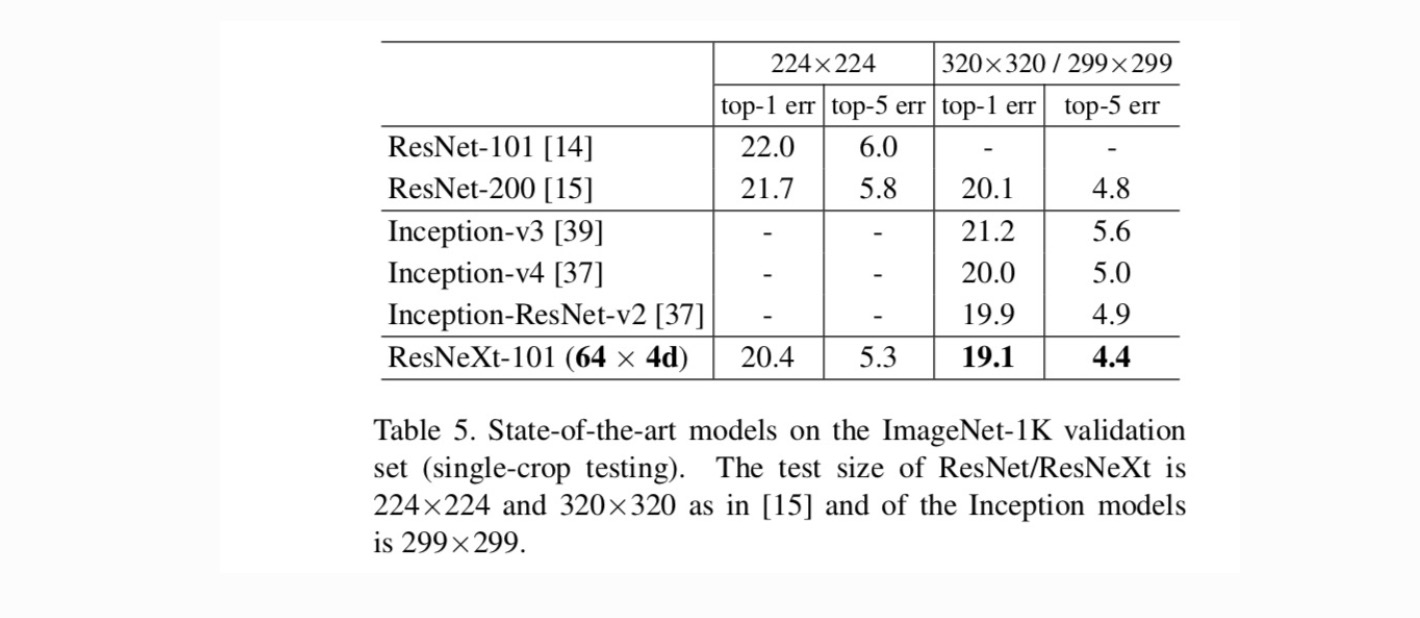
Vergleiche mit State-of-the-art Ergebnissen. Tabelle 5 zeigt weitere Ergebnisse von Single-Crop-Tests mit dem ImageNet-Validierungsset. Unsere Ergebnisse sind im Vergleich zu ResNet, Inception-v3 / v4 und Inception-ResNet-v2 günstig und erreichen eine Single-Crop-Top-5-Fehlerrate von 4,4%. Darüber hinaus ist unser Architekturdesign viel einfacher als alle Inception-Modelle und erfordert erheblich weniger Hyper-Parameter, die von Hand eingestellt werden müssen.