Posted Juni 2008.
Die zweite von zwei Spalten über die Mathematik der Vermessung (die erste ist hier). …
Bill Casselman
Universität von British Columbia, Vancouver, Kanada
cass at math.ubc.ca 
John Eggers
Universität von Kalifornien, San Diego
jeggers an der ucsd.edu
 E-Mail an einen Freund E-Mail an einen Freund |
 Diesen Artikel drucken Diesen Artikel drucken |
Ein Planimeter ist ein Tischgerät zum Messen von Bereichen, normalerweise die Bereiche unregelmäßiger Regionen auf einer Karte oder einem Foto. Sie waren einst üblich, wurden aber inzwischen weitgehend durch digitale Tools ersetzt.
Das folgende Bild gibt einen Eindruck vom Setup. Der Stangenarm dreht sich frei um die Stange, die auf dem Tisch befestigt ist. Der Tracerarm dreht sich um den Drehpunkt, an dem er sich mit dem Polararm verbindet. Sie verfolgen eine Kurve im Uhrzeigersinn mit dem Tracer, und während Sie dies tun, rollt das Messrad entlang, und die Gesamtstrecke, die es rollt, wird auf dem Zifferblatt akkumuliert. Das Stützrad verhindert, dass das Ding umkippt. Am Ende lesen Sie eine Zahl vom Zifferblatt ab und nach Multiplikation mit einem Faktor, der nur von der jeweiligen Konfiguration des Planimeters abhängt, erhalten Sie den Bereich innerhalb der Kurve.

Die nächste Abbildung gibt Ihnen einen besseren Überblick über den Mechanismus.

Wir nennen den Wagen die Montage von Rädern, Zifferblatt und Drehpunkt. Im nächsten Bild sehen Sie es sich besser an und können den Schneckenantrieb sehen, der bewirkt, dass sich das Zifferblatt dreht, wenn sich das Messrad bewegt.

Hier ist das Diagramm des ursprünglichen Planimeters aus dem Artikel von Jakob Amsler, der es vorstellte:
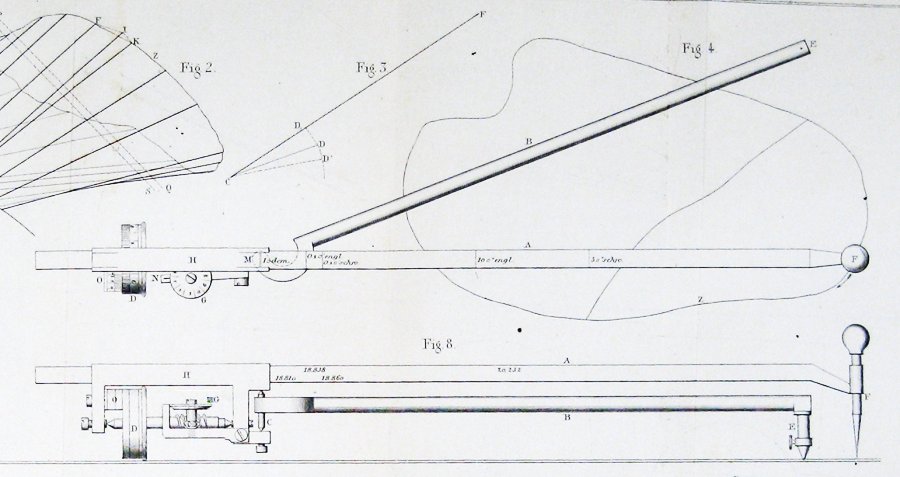
Wie kann so eine einfache Sache Flächen messen?
Geometrie des Planimeters
Die Bewegung des Planimeters im Uhrzeigersinn ist die entgegengesetzte Richtung zu dem, was Mathematiker entschieden haben, sollte positive Rotation sein. Anstatt gegen diese Konvention zu verstoßen, werden wir von nun an mit einem Mathematiker-Planimeter arbeiten, in dem Sie sich gegen den Uhrzeigersinn bewegen. Wie die Fantasien anderer Mathematiker gibt es keine auf dem Planeten!
Es gibt einige Einschränkungen bei der Platzierung des Planimeters in Bezug auf die Kurve, die Sie verfolgen möchten. Der Schlitten kann entlang des Tastarms geschoben werden, jedoch ist in allen Fällen die Länge l des Tastarms kleiner als die Länge r des Polarms. Dies bedeutet, dass der Tracer niemals in eine Entfernung r – l des Pols gelangen kann. Die zu verfolgende Kurve muss also innerhalb des Ringraums zwischen zwei Kreisen liegen, einer mit dem Radius r – l, der andere r + l.

Tatsächlich sollte in einem Moment klar werden, dass die Arme niemals vollständig ausgestreckt werden sollten, sodass die zu verfolgende Kurve vollständig innerhalb des Ringraums liegen muss. Außerdem wird normalerweise der Pfosten auf die Außenseite der Kurve gesetzt.

Für einen gegebenen Punkt im Annulus gibt es genau zwei mögliche Konfigurationen des Planimeters, die den Tracer an diesem Punkt platzieren. Die Wahl des einen oder anderen Punktes bedeutet, ein Zeichen für eine Quadratwurzel zu wählen. Wir nennen dies die Wahl einer Orientierung für das Planimeter. Es ist positiv, wenn die Quadratwurzel positiv ist. Sobald eine Ausrichtung gewählt wurde, bleibt sie dieselbe, es sei denn, der Arm ist vollständig ausgefahren. Das darf niemals passieren. Solange sich Ihre Kurve vollständig innerhalb des Ringraums befindet, variieren die Konfigurationen des Planimeters reibungslos und eindeutig mit dem Pfad des Tracers.
Als nächstes müssen Sie ein paar Dinge über die Bewegung des Messrades verstehen. Wie das folgende Bild zeigt, dreht sich das Rad, wenn das Rad in einer geraden Linie eine Strecke C zurücklegt, um einen Winkel θ = C / R, wobei R sein Radius ist.

Es ist also wirklich wahr, dass die Drehung des Rades und die vom Tastarm zurückgelegte Strecke in irgendeiner Beziehung zueinander stehen. Aber diese Beziehung ist ein bisschen subtil. Wenn sich der Arm nur eine Strecke C geradeaus bewegt, ist der überstrichene Bereich lC, aber wenn er sich parallel zu sich selbst verschiebt, ist der überstrichene Bereich 0. Im ersten Fall bewegt sich ein Punkt am Umfang des Rades um C. Im zweiten Fall bewegt sich das Rad überhaupt nicht. Und wenn der Arm schräg übersetzt, dreht sich das Rad um eine Strecke, die der Höhe des Parallelogramms entspricht, das der Arm zurücklegt. In allen Fällen, in denen sich der Arm parallel zu sich selbst bewegt, ist die Fläche, die von dem Teil des Tastarms zwischen dem Drehpunkt und dem Taststift weggefegt wird, gleich lC, wobei C der Abstand ist, der durch die Drehung des Rades gemessen wird. Dies ist die grundlegende Tatsache, die die Bewegung des Arms mit der Bewegung des Messrades in Beziehung setzt.

Die Art und Weise, dies genau zu formulieren, ist, dass, egal wie sich der Arm bewegt, der vom Rad gemessene Abstand das Pfadintegral ist

wobei Γ der Weg ist, den der Punkt des Arms zurücklegt, an dem das Messrad befestigt ist, n ist der Einheitsvektor senkrecht zum Arm zu jedem Zeitpunkt , und t ist der Einheitsvektor, der in Fahrtrichtung zeigt (so dass beispielsweise, wenn sich der Arm parallel zu sich selbst bewegt, das Punktprodukt von n und t 0 ist).
Guldins Theorem
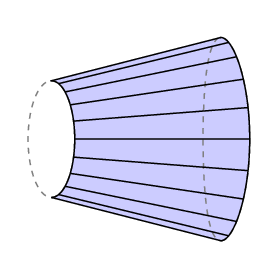
Als nächstes werden wir versuchen, das Verhalten des Planimeters intuitiv klar zu machen, aber zuerst werden wir uns eine spezielle Art von Planimeter ansehen und in diesem Fall ein allgemeineres Ergebnis beweisen. Angenommen, wir nehmen einen einzelnen frei beweglichen Arm der Länge l und befestigen daran ein Messrad mit dem Radius R genau in seiner Mitte.

Dann bewegen wir den Arm im Flugzeug. Wenn sich das Messrad bei der Bewegung des Arms um einen Gesamtwinkel von θ Bogenmaß dreht, beträgt die Strecke, die ein Punkt auf dem Umfang zurücklegt, C = θR.
Satz von Guldin. In dieser Situation ist die Gesamtfläche, die vom Arm weggefegt wird, das Produkt lC.
Bereich wird hier mit einem Vorzeichen interpretiert. Wenn sich der Arm nur um seine Mitte dreht, geht eine Hälfte des Arms vorwärts und die andere rückwärts, und die beiden brechen ab.
Wir haben bereits gesehen, dass Guldins Behauptung für den Fall gültig ist, dass der Arm gerade übersetzt. Natürlich passiert das nicht immer – der Arm kann sich drehen, wenn er sich bewegt, und übersetzen. Aber wir können sehen, was passiert, indem wir den überstrichenen Bereich wie folgt zerhacken:

Da sich das Messrad in der Mitte des Arms befindet, zerquetscht es beim Drehen des Arms die kleinen Blöcke auf der einen Seite, während es sie auf der anderen erweitert. Diese Effekte heben sich genau auf.
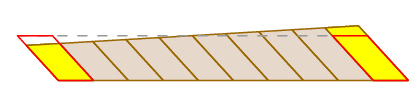
Ein völlig rigoroser Beweis kann durch Verwendung der Formel für die Änderung von Variablen in einem Doppelintegral und des Ausdrucks für den Radweg als Pfadintegral gegeben werden.
Angenommen, das Rad ist woanders platziert. Angenommen, seine Position ist c + v, wobei c die Mitte des Arms und v ein Vektor entlang des Arms ist. Die Länge von v bleibt fest, sagen wir bei ρ. Der Pfad, dem das Rad folgt, ist c (t) + v (t). Das Pfadintegral ist jetzt
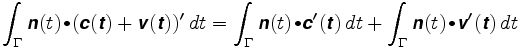
Das erste Integral ist die Strecke, die das Rad zurücklegen würde, wenn es in der Mitte des Arms wäre. Im zweiten Fall ist der Vektor v (t) immer senkrecht zu n und v (t) hat eine konstante Länge. Der Vektor v(t) bewegt sich auf einem Kreis mit dem Radius ρ. Daher ist das Punktprodukt von n und v'(t) nur die vorzeichenbehaftete Länge von v'(t), und das zweite Integral ist gleich ρ mal der Gesamtrotation des Arms. Daher:
Wenn das Rad einen Abstand ρ von der Mitte des Arms hat, ist der Abstand C, den das Rad misst, C0 , der Abstand, der gemessen würde, wenn das Rad in der Mitte wäre, plus ρ mal dem Gesamtwinkel θ, den der Arm dreht.
Sie können sofort einen einfachen Fall davon sehen, indem Sie den Arm um seine Mitte drehen. Wenn wir dies mit dem Satz von Guldin kombinieren, sehen wir, dass in allen Fällen:
C = C0 + ρ θ
Area swept out = l C0 = l C – l ρ θ
Das vollständige Ergebnis
Guldins Formel gibt einen vorzeichenbehafteten Bereich an – wenn Sie rückwärts über einen Bereich streichen, geht das Rad rückwärts und Sie stornieren den Bereich, den Sie bereits abgedeckt haben. Wenn wir dies auf den Fall anwenden, dass der freie Arm genau dorthin zurückkehrt, wo er begonnen hat, sehen wir, dass lC gleich der Fläche des geschlossenen Bereichs ist, der vom rechten Ende des Arms verfolgt wird, minus der Fläche des vom linken überstrichenen Bereichs.

Im Falle des Polarplanimeters ist die Unterseite des Arms auf einen Kreisbogen des Radius r mit Zentrum am Pol beschränkt, daher ist lc der vom Tracer verfolgte Bereich. Außerdem liegt der Pol normalerweise außerhalb des zu messenden Bereichs, und in diesem Fall muss der Gesamtumdrehungsbetrag des Arms 0 sein. In diesem Fall haben wir also
Area of the region traced = lC
Hier ist die Zahl, die Jakob Amsler, der Erfinder, in seiner Originalarbeit über das von ihm erfundene Instrument aufgenommen hat:
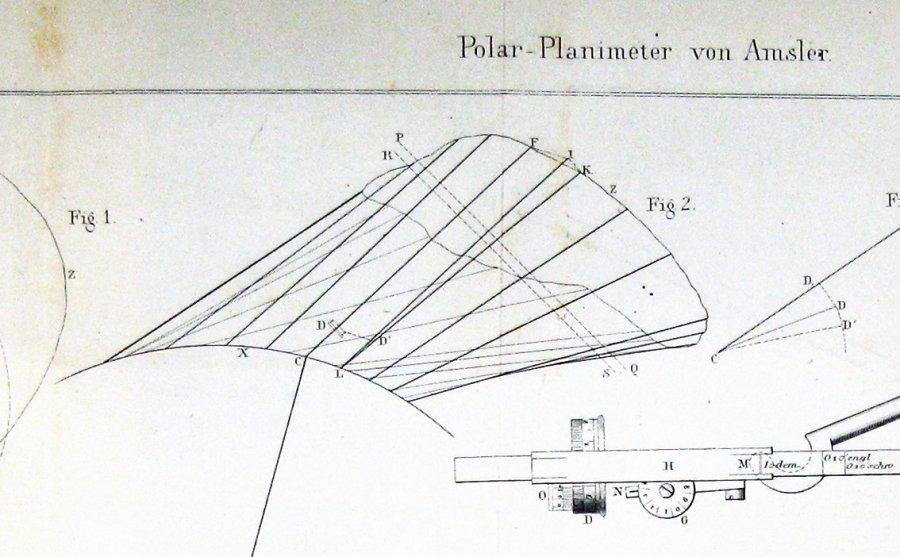
Daraus scheint ziemlich klar zu sein, dass Amsler seine Konstruktion durch eine Form von Guldins Theorem abgeleitet hat.
Planimeter und Green’s Theorem
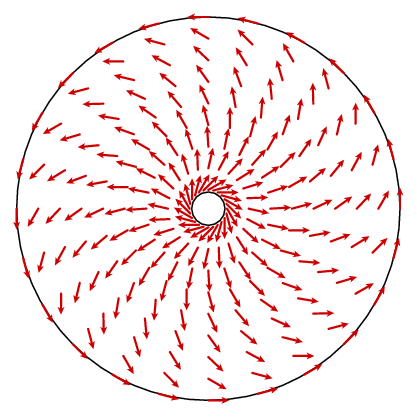
Wie bereits erwähnt, ist die Planimeterkonfiguration nach Wahl der Ausrichtung des Planimeters eine stetige Funktion der Tracerposition. Sagen wir, wir wählen die positive Orientierung. Dann können wir an jedem Punkt des Ringes einen Einheitsvektor n anbringen, der gegen den Uhrzeigersinn und senkrecht zum Tracerarm am Tracer zeigt.
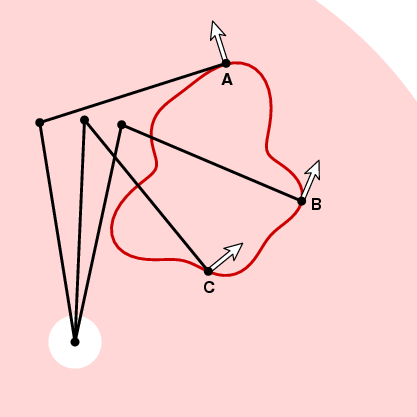
Wie das Messrad im nächsten Moment auf eine Bewegung entlang der Kurve reagiert, hängt vom Winkel zwischen diesem Vektor und dem Einheits-Tangentenvektor der Kurve ab. Bei A im Bild oben bewegt sich das Messrad nicht, da die Bewegung entlang der Kurve parallel zum Tastarm verläuft. Bei B bewegt sich der Tracer eine kleine Strecke ds, so bewegt sich auch das Messrad. Und bei C bewegt sich das Messrad etwas zwischen 0 und ds. Um genau zu sein, angenommen, t ist der Einheitstangensvektor an einem bestimmten Punkt der Kurve. Wenn der Tracer die Strecke ds entlang der Kurve bewegt, bewegt das Messrad an diesem Punkt eine Strecke d ds, wobei d = n ist. t, das Punktprodukt der Einheitsvektoren t und n. Mit anderen Worten, wenn wir uns um die Kurve Γ bewegen, bewegt sich das Messrad um eine Gesamtstrecke, die dem Integral von n entspricht . t ds (Punktprodukt) oder

Da jedoch jeder Punkt des Ringes einer eindeutigen positiven Konfiguration des Planimeters entspricht, können wir jedem inneren Punkt des Ringes einen Vektor n zuweisen, der daher ein Vektorfeld definiert. Die Kurve Γ ist die Grenze ihres Inneren Ω, und nach einer unserer Annahmen ist diese vollständig in dem Bereich enthalten, in dem n definiert ist. Der Satz von Green sagt uns, dass das Pfadintegral um die Grenze dieser Region auch gleich einem bestimmten Integral über Ω ist: Daher
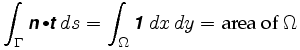
Genauer gesagt sagt uns Green’s Theorem, dass
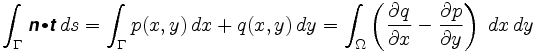
wobei n = das Vektorfeld ist. Der Integrande im Doppelintegral wird als Curl des Vektorfeldes bezeichnet.
Das scheint uns nicht sehr weit zu bringen. Was passieren sollte, ist, dass die Locke eine konstante 1 ist. Im Prinzip könnten wir eine Formel für das Vektorfeld n finden und seine Krümmung berechnen, aber das ist nicht sehr aufschlussreich. Wir können jedoch eine andere Tatsache ausnutzen. Das Vektorfeld hat eine Kreissymmetrie, was bedeutet, dass es durch das bestimmt wird, was es auf einem Radius ist. Das Kosinusgesetz gibt uns eine einfache Formel für die Umfangskomponente.
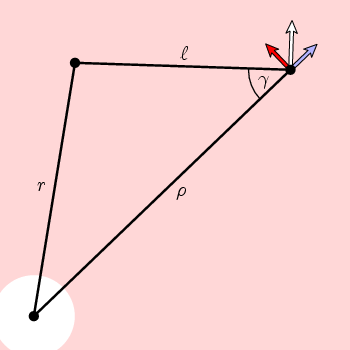
Aus der einfachen Geometrie in dieser Abbildung folgt, dass die Umfangskomponente von n
f(ρ) = cos(γ) = (ρ 2 + l 2 – r 2)/(2 ρ l)
Der eigentliche Punkt von Greens Theorem ist, dass es ausreicht, um zu überprüfen, ob der Integrande 1 ist, zu überprüfen, ob das Pfadintegral um geeignete kleine Pfade gleich ist wie das Gebiet. Dafür wählen wir unsere Regionen wie hier aus:
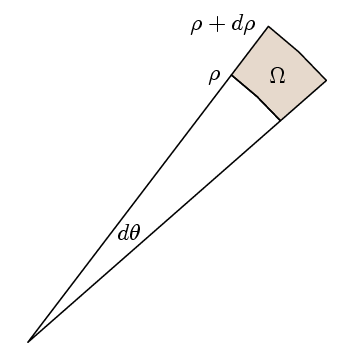
Dann ist l mal das Pfadintegral
l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ
oder
(θ/2) ( (ρ + dp) 2 – ρ 2)
Das ist die Fläche der Region Ω.
Andere Arten von Planimetern
Guldins Theorem impliziert, dass die Bewegung eines Messrades den vom Tracer verfolgten Bereich angibt, wenn der Arm mit einem Messrad eine Kurve nachzeichnet, aber ein Ende auf eine eindimensionale Kurve beschränkt ist. Dies geschieht beispielsweise mit dem Rollhobel, bei dem der Drehpunkt auf einer Geraden beschränkt ist, indem er sich auf einem Rollzylinder befindet.

Um mehr zu erfahren
-
 produziert und verkauft immer noch Planimeter.
produziert und verkauft immer noch Planimeter. - Differential- und Integralrechnung Band II, R. Courant, Blackie & Sohn, 1936. Der Abschnitt über Guldins Formel (S. 294-298) bietet eine Erklärung der Funktionsweise des Planimeters.
- Amslers Originalartikel, Vierteljahresschrift der Naturforschenden Gesellschaft in Zürich, 1856. Hier fehlen die Diagramme, aber sie sind hier:
- Amslers erstes Diagramm
- Amslers zweites Diagramm
Unser Dank geht an Donna Sammis von der Stony Brook University Library für das Auffinden des Artikels und an ihren Ehemann Robert für die Bereitstellung von Fotos der Figuren.
Das von Amsler gegründete Unternehmen produzierte Instrumente bis weit ins 20.Jahrhundert hinein. Dieses Foto zeigt das Logo auf einer Pantograph-Version des Planimeters:

- „About Planimeters,“ EngineerSupply. Das Unternehmen hat auch ein Video auf YouTube gepostet.
Bill Casselman
Universität von British Columbia, Vancouver, Kanada
cass at math.ubc.ca 
John Eggers
Universität von Kalifornien, San Diego
jeggers bei ucsd.edu 
Diejenigen, die auf JSTOR zugreifen können, finden dort einige der oben genannten Artikel. Für diejenigen mit Zugang kann das MathSciNet der American Mathematical Society verwendet werden, um zusätzliche bibliografische Informationen und Rezensionen einiger dieser Materialien zu erhalten. Auf einige der oben genannten Elemente kann über das ACM-Portal zugegriffen werden , das auch bibliografische Dienste bereitstellt.