Einführung in die Bewegungsschätzung mit optischem Fluss

In diesem Tutorial tauchen wir in die Grundlagen des optischen Flusses ein, betrachten einige seiner Anwendungen und implementieren seine zwei Hauptvarianten (sparse und dense). Wir diskutieren auch kurz neuere Ansätze mit Deep Learning und vielversprechende zukünftige Richtungen.

Jüngste Durchbrüche in der Computer-Vision-Forschung haben es Maschinen ermöglicht, ihre umgebende Welt durch Techniken wie Objekterkennung zum Erkennen von Instanzen von Objekten, die zu einer bestimmten Klasse gehören, und semantische Segmentierung zur pixelweisen Klassifizierung wahrzunehmen.Für die Verarbeitung von Echtzeit-Videoeingängen adressieren die meisten Implementierungen dieser Techniken jedoch nur Beziehungen von Objekten innerhalb desselben Frames \((x, y)\), wobei Zeitinformationen \((t)\) außer Acht gelassen werden. Mit anderen Worten, sie bewerten jeden Frame für jeden Lauf unabhängig voneinander neu, als wären es völlig unabhängige Bilder. Was ist jedoch, wenn wir die Beziehungen zwischen aufeinanderfolgenden Frames benötigen, um beispielsweise die Bewegung von Fahrzeugen über Frames hinweg zu verfolgen, um die aktuelle Geschwindigkeit zu schätzen und ihre Position im nächsten Frame vorherzusagen?

Oder, alternativ, was ist, wenn wir Informationen über menschliche Pose-Beziehungen zwischen aufeinanderfolgenden Frames benötigen, um menschliche Aktionen wie Bogenschießen, Baseball und Basketball zu erkennen?

In diesem Tutorial erfahren wir, was Optischer Fluss ist, wie seine beiden Hauptvarianten (sparse und Dense) implementiert werden können, und erhalten ein umfassendes Bild von neueren Ansätzen mit Deep Learning und vielversprechenden zukünftigen Richtungen.

Was ist optischer Fluss?
Implementierung eines spärlichen optischen Flusses
Implementierung eines dichten optischen Flusses
Deep Learning und darüber hinaus

Was ist optischer Fluss?

Beginnen wir mit einem allgemeinen Verständnis des optischen Flusses. Der optische Fluss ist die Bewegung von Objekten zwischen aufeinanderfolgenden Sequenzbildern, die durch die Relativbewegung zwischen Objekt und Kamera verursacht wird. Das Problem des optischen Flusses kann ausgedrückt werden als:

wobei wir zwischen aufeinanderfolgenden Bildern die Bildintensität \((I)\) als Funktion von Raum \((x, y)\) und Zeit \((t)\((t)\)\(( )\). Mit anderen Worten, wenn wir das erste Bild \(I(x, y, t)\) nehmen und seine Pixel um \((dx, dy)\) über \(t\) Zeit verschieben, erhalten wir das neue Bild \(I(x + dx, y + dy, t + dt)\) .

Zunächst nehmen wir an, dass die Pixelintensitäten eines Objekts zwischen aufeinanderfolgenden Frames konstant sind.

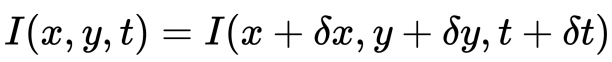
Zweitens nehmen wir die Taylor-Reihen-Approximation der RHS und entfernen gebräuchliche Begriffe.

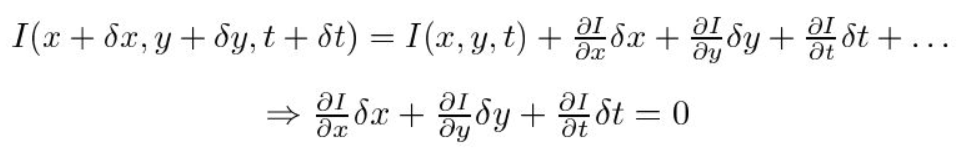
Drittens dividieren wir durch \(dt\), um die optische Flussgleichung abzuleiten:

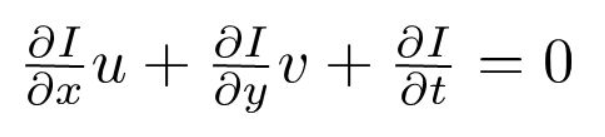
wobei \(u = dx/dt\) und \(v = dy/dt\).

\(dI/dx, dI/dy\) und \(dI/dt\) sind die Bildverläufe entlang der horizontalen Achse, der vertikalen Achse und der Zeit. Daher schließen wir mit dem Problem des optischen Flusses, das heißt, Lösen \ (u (dx / dt) \) und \(v (dy / dt) \), um die Bewegung über die Zeit zu bestimmen. Sie werden feststellen, dass wir die optische Flussgleichung für \ (u \) und \ (v \) nicht direkt lösen können, da es nur eine Gleichung für zwei unbekannte Variablen gibt. Wir werden einige Methoden wie die Lucas-Kanade-Methode implementieren, um dieses Problem zu beheben.

Sparse vs Dense Optical Flow

Sparse optical Flow liefert die Flussvektoren einiger „interessanter Merkmale“ (z. B. wenige Pixel, die die Kanten oder Ecken eines Objekts darstellen) innerhalb des Rahmens, während Dense optical Flow die Flussvektoren des gesamten Rahmens (alle Pixel) liefert – bis zu einem Flussvektor pro Pixel. Wie Sie vermutet haben, hat der dichte optische Fluss eine höhere Genauigkeit auf Kosten von langsam / rechenintensiv.

Sparse Optical Flow implementieren

Sparse optical flow wählt einen Sparse-Feature-Satz von Pixeln (z. B. interessante Features wie Kanten und Ecken) aus, um seine Geschwindigkeitsvektoren (Bewegung) zu verfolgen. Die extrahierten Merkmale werden in der optischen Flussfunktion von Bild zu Bild übergeben, um sicherzustellen, dass dieselben Punkte verfolgt werden. Es gibt verschiedene Implementierungen des spärlichen optischen Flusses, einschließlich der Lucas-Kanade-Methode, der Horn-Schunck-Methode, der Buxton–Buxton-Methode und mehr. Wir werden die Lucas-Kanade-Methode mit OpenCV, einer Open-Source-Bibliothek von Computer-Vision-Algorithmen, für die Implementierung verwenden.

Einrichten Ihrer Umgebung

Wenn Sie OpenCV noch nicht installiert haben, öffnen Sie das Terminal und führen Sie Folgendes aus:

pip install opencv-python

Klonen Sie nun das Tutorial-Repository, indem Sie Folgendes ausführen:

git clone https://github.com/chuanenlin/optical-flow.git

parse-starter.py mit Ihrem Texteditor. Wir werden den gesamten Code in diese Python-Datei schreiben.

Konfigurieren von OpenCV zum Lesen eines Videos und Einrichten von Parametern

Shi-Tomasi Corner Detector – Auswählen der zu verfolgenden Pixel

Für die Implementierung eines spärlichen optischen Flusses verfolgen wir nur die Bewegung eines Feature-Sets von Pixeln. Merkmale in Bildern sind Points of Interest, die reichhaltige Bildinhaltsinformationen enthalten. Beispielsweise können solche Merkmale Punkte im Bild sein, die für Translations-, Skalierungs-, Rotations- und Intensitätsänderungen wie Ecken invariant sind.

Der Shi-Tomasi Corner Detector ist dem beliebten Harris Corner Detector sehr ähnlich, der durch die folgenden drei Verfahren implementiert werden kann:

1. Bestimmen Sie Fenster (kleine Bildflecken) mit großen Gradienten (Variationen in der Bildintensität), wenn sie in \ (x \) und \(y\) Richtungen übersetzt werden.
2. Berechnen Sie für jedes Fenster eine Punktzahl \(R\).
3. Abhängig vom Wert von \(R\) wird jedes Fenster als Flach, Kante oder Ecke klassifiziert.

Wenn Sie mehr über eine schrittweise mathematische Erklärung des Harris Corner Detector erfahren möchten, können Sie diese Folien gerne durchgehen.

Shi und Tomasi machten später eine kleine, aber effektive Modifikation des Harris Corner Detector in ihrem Papier Good Features to Track.

Die Modifikation bezieht sich auf die Gleichung, in der score \(R\) berechnet wird. Im Harris Corner Detector ist die Scoring-Funktion gegeben durch:

$$
\beginnen{array}{c}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\Zeilenumbruch \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\Zeilenumbruch \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\Ende{array}
$$

Stattdessen schlug Shi-Tomasi die Bewertungsfunktion wie folgt vor:

$$
R=\min \left(\lambda_{1}, \lambda_{2}\right)
$$

was im Grunde bedeutet, wenn \(R\) größer als ein Schwellenwert ist, wird es als Ecke klassifiziert. Im Folgenden werden die Bewertungsfunktionen von Harris (links) und Shi-Tomasi (rechts) im Raum \ (λ1-λ2\) verglichen.

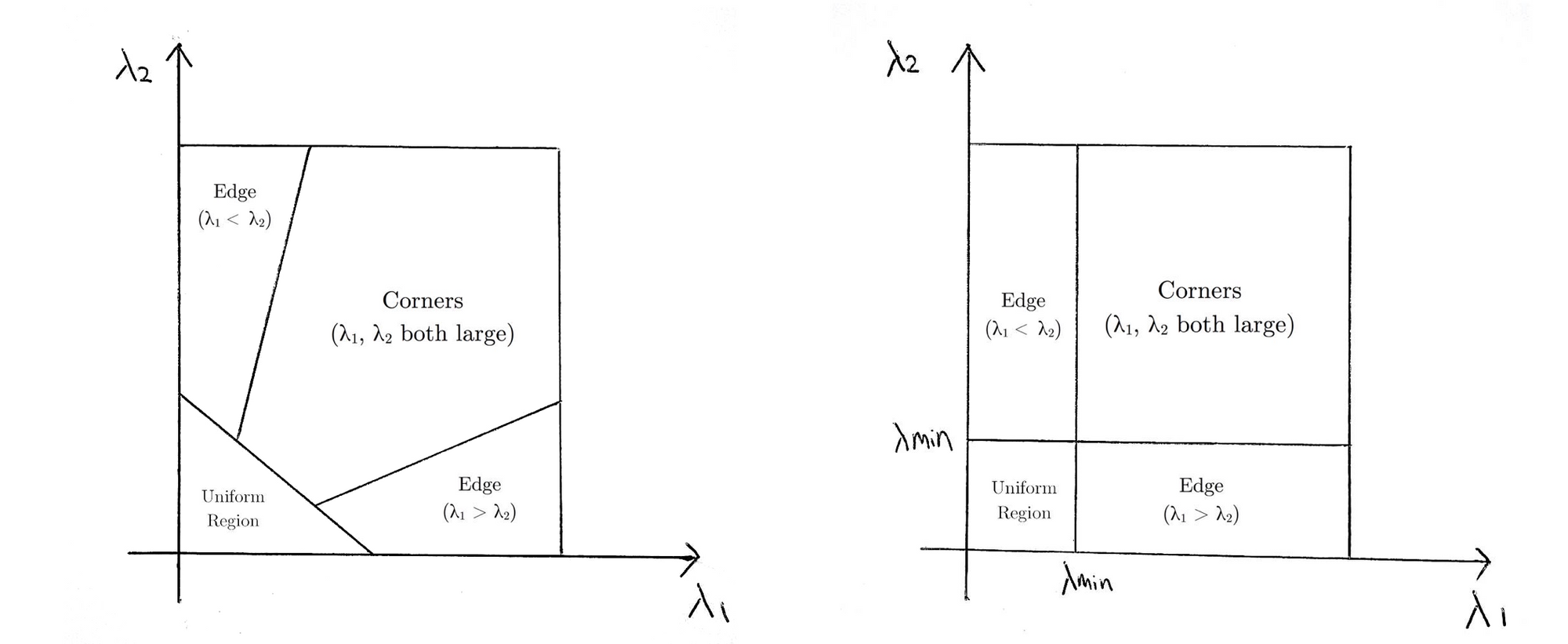
Für Shi-Tomasi wird das Fenster nur dann als Ecke klassifiziert, wenn \(λ1\) und \(λ2\) über einem Mindestschwellenwert \(λmin\) liegen.

Die Dokumentation der OpenCV-Implementierung von Shi-Tomasi über goodFeaturesToTrack() finden Sie hier .

Verfolgung bestimmter Objekte

Es kann Szenarien geben, in denen Sie nur ein bestimmtes Objekt von Interesse (z. B. Verfolgung einer bestimmten Person) oder eine Kategorie von Objekten (z. B. alle 2-Wheeler-Fahrzeuge im Verkehr) verfolgen möchten. Sie können den Code einfach ändern, um die Pixel der gewünschten Objekte zu verfolgen, indem Sie die Variable prev ändern.

Sie können die Objekterkennung auch mit dieser Methode kombinieren, um nur den Pixelfluss innerhalb der erkannten Begrenzungsrahmen zu schätzen. Auf diese Weise können Sie alle Objekte eines bestimmten Typs / einer bestimmten Kategorie im Video verfolgen.

Lucas-Kanade: Sparse Optical Flow

Lucas und Kanade schlugen eine effektive Technik vor, um die Bewegung interessanter Merkmale abzuschätzen, indem sie zwei aufeinanderfolgende Frames in ihrem Papier Eine iterative Bildregistrierungstechnik mit einer Anwendung auf Stereovision verglichen. Die Lucas-Kanade-Methode arbeitet unter folgenden Annahmen:

1. Zwei aufeinanderfolgende Frames werden durch ein kleines Zeitinkrement (\(dt\)) getrennt, so dass Objekte nicht signifikant verschoben werden (mit anderen Worten, die Methode funktioniert am besten mit sich langsam bewegenden Objekten).
2. Ein Rahmen zeigt eine „natürliche“ Szene mit strukturierten Objekten, die Grautöne aufweisen, die sich sanft ändern.

Zunächst können wir unter diesen Annahmen ein kleines 3×3-Fenster (Nachbarschaft) um die von Shi-Tomasi erkannten Merkmale nehmen und annehmen, dass alle neun Punkte die gleiche Bewegung haben.

Lucas-Kanade: Der optische Fluss wird für die schwarzen Pixel geschätzt

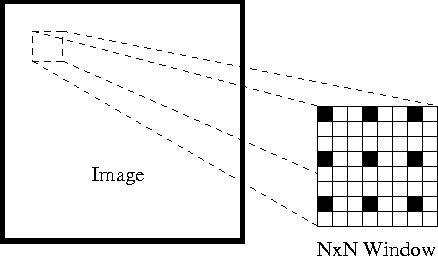
Dies kann dargestellt werden als

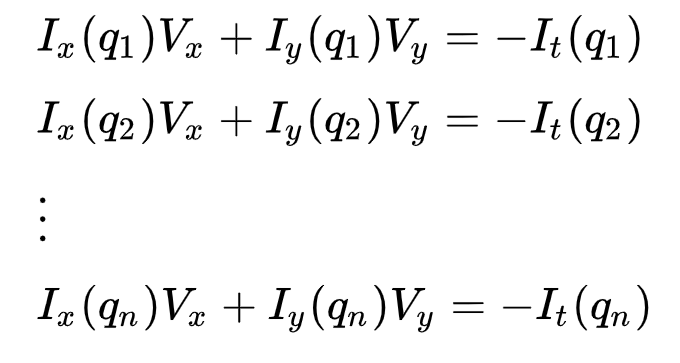
wobei \(q_1, q_2, …, q_n\) die Pixel innerhalb des Fensters bezeichnen (z. B. \(n\) = 9 für ein 3×3-Fenster) und \(I_x(q_i)\), \(I_y(q_i)\) und \(I_t(q_i)\) die partiellen Ableitungen des Bildes \(I\) in Bezug auf die Position \((x, y)\ ) und Zeit \(t\), für Pixel \(q_i\) zur aktuellen Zeit.

Dies ist nur die optische Flussgleichung (die wir zuvor beschrieben haben) für jedes der n Pixel.

Der Satz von Gleichungen kann in der folgenden Matrixform dargestellt werden, wobei \(Av = b\):

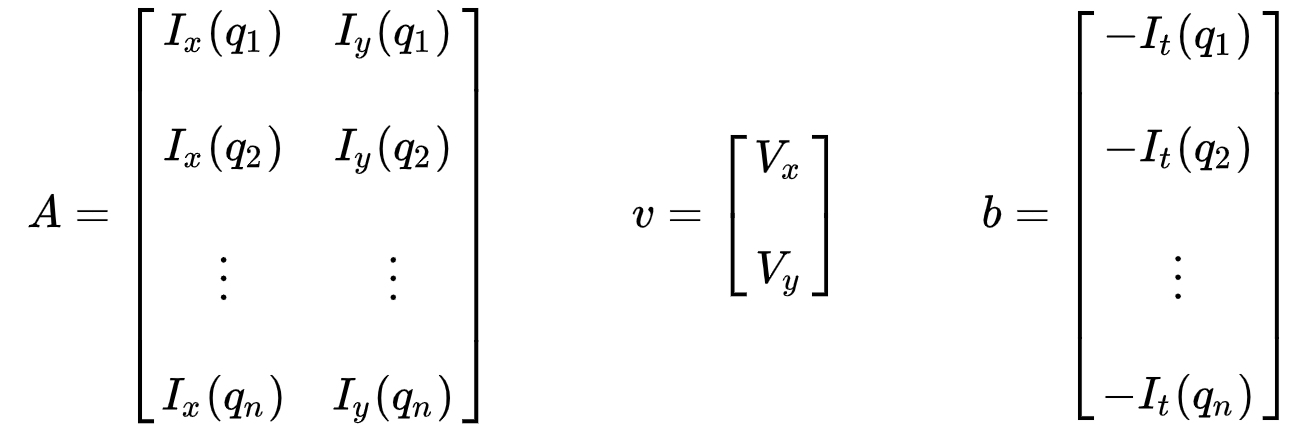
Beachten Sie, dass zuvor (siehe „Was ist optischer Fluss?“ Abschnitt) standen wir vor dem Problem, zwei unbekannte Variablen mit einer Gleichung lösen zu müssen. Wir müssen nun mit neun Gleichungen nach zwei Unbekannten (\(V_x \) und \ (V_y \)) lösen, was überbestimmt ist.

Zweitens, um das überbestimmte Problem anzugehen, wenden wir die Anpassung der kleinsten Quadrate an, um das folgende Zwei-Gleichungen-Zwei-Unbekannte-Problem zu erhalten:

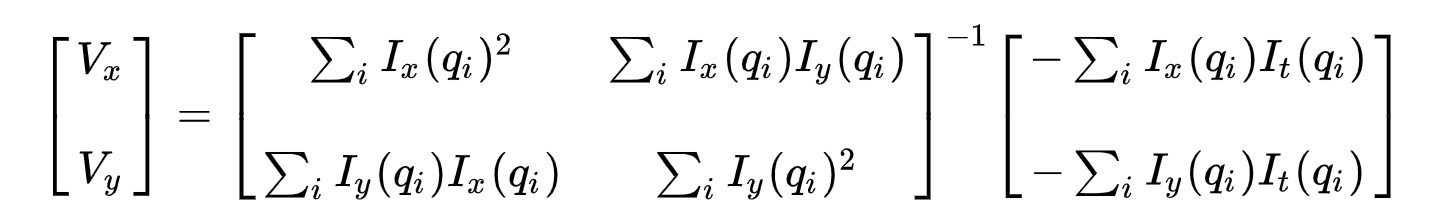
wobei \(Vx = u = dx/dt\) die Bewegung von \(x\) über die Zeit und \(Vy = v = dy/dt\) die Bewegung von y über die Zeit bezeichnet. Die Lösung für die beiden Variablen vervollständigt das Problem des optischen Flusses.

Kurz gesagt, wir identifizieren einige interessante Funktionen, um die optischen Flussvektoren dieser Punkte zu verfolgen und iterativ zu berechnen. Die Lucas-Kanade-Methode funktioniert jedoch nur für kleine Bewegungen (aus unserer ursprünglichen Annahme) und schlägt fehl, wenn große Bewegungen vorliegen. Daher übernimmt die OpenCV-Implementierung der Lucas-Kanade-Methode Pyramiden.

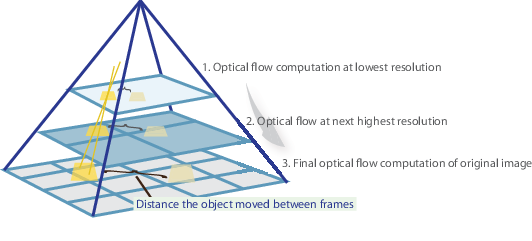
In einer High-Level-Ansicht werden kleine Bewegungen vernachlässigt, wenn wir die Pyramide hinaufgehen, und große Bewegungen werden auf kleine Bewegungen reduziert – wir berechnen den optischen Fluss zusammen mit der Skalierung. Eine umfassende mathematische Erklärung der OpenCV-Implementierung finden Sie in Bouguets Notizen und die Dokumentation der OpenCV-Implementierung der Lucas-Kanade-Methode über calcOpticalFlowPyrLK() finden Sie hier .

Visualisieren

Und das war’s! Öffnen Sie das Terminal und führen Sie

python sparse-starter.py

aus, um Ihre Implementierung des spärlichen optischen Flusses zu testen. 👏

Falls Sie einen Code verpasst haben, finden Sie den vollständigen Code in sparse-solution.py.

Implementieren eines dichten optischen Flusses

Wir haben zuvor den optischen Fluss für einen spärlichen Feature-Set von Pixeln berechnet. Dense Optical Flow versucht, den optischen Flussvektor für jedes Pixel jedes Frames zu berechnen. Während eine solche Berechnung langsamer sein kann, liefert sie ein genaueres Ergebnis und ein dichteres Ergebnis, das für Anwendungen wie das Lernen von Strukturen aus Bewegung und Videosegmentierung geeignet ist. Es gibt verschiedene Implementierungen des dichten optischen Flusses. Wir werden die Farneback-Methode, eine der beliebtesten Implementierungen, mit OpenCV, einer Open-Source-Bibliothek von Computer-Vision-Algorithmen, für die Implementierung verwenden.

Einrichten Ihrer Umgebung

Wenn Sie dies noch nicht getan haben, folgen Sie bitte Schritt 1 der Implementierung von Sparse Optical Flow, um Ihre Umgebung einzurichten.

Weiter, öffnen dense-starter.py mit Ihrem Texteditor. Wir werden den gesamten Code in diese Python-Datei schreiben.

Konfigurieren von OpenCV zum Lesen eines Videos

Farneback Optical Flow

Gunnar Farneback schlug in seiner Arbeit Two-Frame Motion Estimation Based on Polynomial Expansion eine effektive Technik zur Schätzung der Bewegung interessanter Merkmale vor, indem er zwei aufeinanderfolgende Frames vergleicht.Zunächst approximiert die Methode die Fenster (siehe Lucas Kanade Abschnitt der Sparse Optical Flow Implementierung für weitere Details) von Bildrahmen durch quadratische Polynome durch Polynomexpansionstransformation. Zweitens wird durch Beobachtung, wie sich das Polynom unter Translation (Bewegung) transformiert, eine Methode zur Schätzung von Verschiebungsfeldern aus Polynomausdehnungskoeffizienten definiert. Nach einer Reihe von Verfeinerungen wird der dichte optische Fluss berechnet. Farneback Papier ist ziemlich prägnant und einfach zu folgen, so empfehle ich durch das Papier gehen, wenn Sie ein besseres Verständnis seiner mathematischen Ableitung möchten.

Für die Implementierung von OpenCV berechnet es die Größe und Richtung des optischen Flusses aus einem 2-Kanal-Array von Flussvektoren \((dx/ dt, dy/dt)\), dem optischen Flussproblem. Es visualisiert dann den Winkel (Richtung) des Flusses nach Farbton und den Abstand (Größe) des Flusses nach Wert der HSV-Farbdarstellung. Die Stärke des HSV ist für optimale Sichtbarkeit immer auf maximal 255 eingestellt. Die Dokumentation der OpenCV-Implementierung der Farneback-Methode über calcOpticalFlowFarneback() finden Sie hier .

Visualisieren

Und das war’s! Öffnen Sie das Terminal und führen Sie

python dense-starter.py

aus, um Ihre Implementierung des dichten optischen Flusses zu testen. 👏

Falls Sie einen Code verpasst haben, finden Sie den vollständigen Code in dense-solution.py .

Optischer Fluss mit Deep Learning

Während das Problem des optischen Flusses in der Vergangenheit ein Optimierungsproblem war, haben neuere Ansätze durch Anwendung von Deep Learning beeindruckende Ergebnisse gezeigt. Im Allgemeinen nehmen solche Ansätze zwei Videobilder als Eingabe, um den optischen Fluss (farbcodiertes Bild) auszugeben, was ausgedrückt werden kann als:

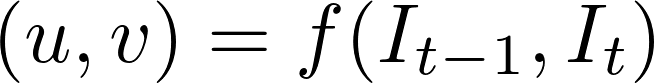
wobei \(u\) die Bewegung in der \(x\) -Richtung ist, \(v\) die Bewegung in der \(y\) -Richtung ist und \(f\) ein neuronales Netzwerk ist, das zwei aufeinanderfolgende Frames \(I_{t-1}\) (frame at time = \(t-1)\) und \(I_t\) (frame at time = \(t)\).

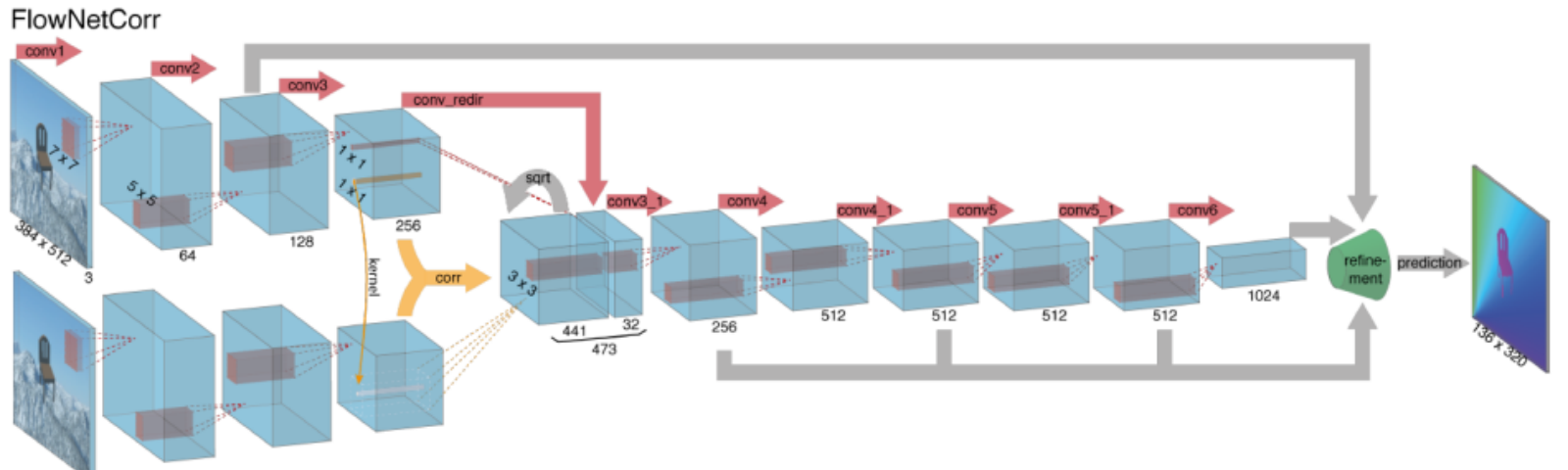
Die Berechnung des optischen Flusses mit tiefen neuronalen Netzen erfordert große Mengen an Trainingsdaten, die besonders schwer zu erhalten sind. Dies liegt daran, dass das Beschriften von Videomaterial für den optischen Fluss eine genaue Ermittlung der genauen Bewegung jedes einzelnen Punkts eines Bildes mit Subpixelgenauigkeit erfordert. Um das Problem der Kennzeichnung von Trainingsdaten anzugehen, verwendeten die Forscher Computergrafiken, um massive realistische Welten zu simulieren. Da die Welten durch Anweisung erzeugt werden, ist die Bewegung jedes einzelnen Punktes eines Bildes in einer Videosequenz bekannt. Einige Beispiele hierfür sind MPI-Sintel, ein Open-Source-CGI-Film mit optischer Flussbeschriftung, der für verschiedene Sequenzen gerendert wurde, und Flying Chairs, ein Datensatz vieler Stühle, die über zufällige Hintergründe fliegen, ebenfalls mit optischer Flussbeschriftung.

Die Lösung von Problemen mit dem optischen Fluss mit Deep Learning ist derzeit ein äußerst heißes Thema, wobei sich Varianten von FlowNet, SPyNet, PWC-Net und mehr in verschiedenen Benchmarks gegenseitig übertreffen.

Anwendung des optischen Flusses: Semantische Segmentierung

Das optische Flussfeld ist eine riesige Informationsquelle für die beobachtete Szene. Da sich die Techniken zur genauen Bestimmung des optischen Flusses verbessern, ist es interessant, Anwendungen des optischen Flusses in Verbindung mit mehreren anderen grundlegenden computergestützten Aufgaben zu sehen. Zum Beispiel besteht die Aufgabe der semantischen Segmentierung darin, ein Bild in eine Reihe von Regionen zu unterteilen, die eindeutigen Objektklassen entsprechen, aber eng platzierte Objekte mit identischen Texturen sind für Single-Frame-Segmentierungstechniken oft schwierig. Wenn die Objekte jedoch getrennt platziert werden, können die unterschiedlichen Bewegungen der Objekte sehr hilfreich sein, wenn Diskontinuitäten im dichten optischen Flussfeld Grenzen zwischen Objekten entsprechen.

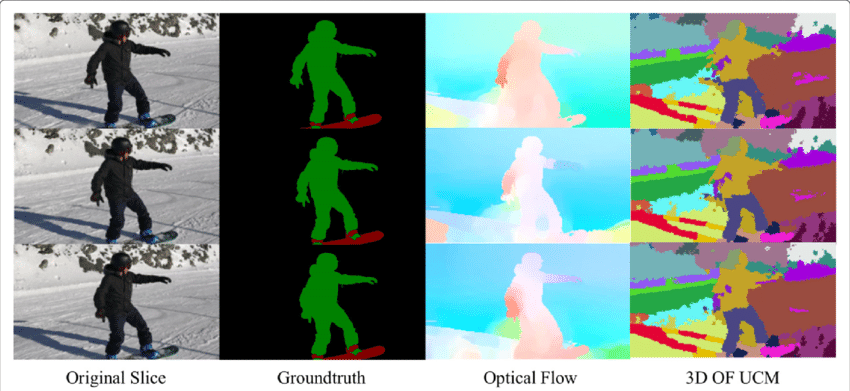
Anwendung des optischen Flusses: Objekterkennung & Tracking

Eine weitere vielversprechende Anwendung des optischen Flusses kann bei der Objekterkennung und -verfolgung oder in einer übergeordneten Form beim Aufbau von Echtzeit-Fahrzeugverfolgungs- und Verkehrsanalysesystemen liegen. Da der spärliche optische Fluss die Verfolgung von Punkten von Interesse verwendet, können solche Echtzeitsysteme durch merkmalsbasierte optische Flusstechniken entweder von einer stationären Kamera oder von an Fahrzeugen angebrachten Kameras durchgeführt werden.

Fazit

Grundsätzlich dienen optische Flussvektoren als Eingabe für eine Vielzahl von übergeordneten Aufgaben, die das Verständnis von Videosequenzen erfordern, während diese Aufgaben als Bausteine für noch komplexere Systeme wie Gesichtsausdrucksanalyse, autonome Fahrzeugnavigation und vieles mehr fungieren können. Neue Anwendungen für den optischen Fluss, die noch entdeckt werden müssen, sind nur durch den Einfallsreichtum seiner Designer begrenzt.

Lazy to Code, willst du nicht für GPUs ausgeben? Gehen Sie zu Nanonets und bauen Sie kostenlos Computer-Vision-Modelle!