In der Praxis des maschinellen und tiefen Lernens sind Modellparameter die Eigenschaften von Trainingsdaten, die während des Trainings durch den Klassifikator oder ein anderes ML-Modell von selbst lernen. Zum Beispiel Gewichte und Verzerrungen oder geteilte Punkte im Entscheidungsbaum.
Modellhyperparameter sind stattdessen Eigenschaften, die den gesamten Trainingsprozess steuern. Dazu gehören Variablen, die die Netzwerkstruktur bestimmen (z. B. Anzahl der versteckten Einheiten), und Variablen, die bestimmen, wie das Netzwerk trainiert wird (z. B. Lernrate). Modellhyperparameter werden vor dem Training festgelegt (bevor die Gewichte und die Vorspannung optimiert werden).
Hier sind zum Beispiel einige im Modell integrierte Konfigurationsvariablen:
- Lernrate
- Anzahl der Epochen
- Versteckte Ebenen
- Versteckte Einheiten
- Aktivierungsfunktionen
Hyperparameter sind wichtig, da sie das Verhalten des Trainingsalgo direkt steuern und einen wichtigen Einfluss auf die Leistung des zu trainierenden Modells haben.Die Auswahl geeigneter Hyperparameter spielt angesichts der Auswirkungen auf das gelernte Modell eine Schlüsselrolle für den Erfolg neuronaler Netzwerkarchitekturen. Zum Beispiel, wenn die Lernrate zu niedrig ist, wird das Modell die wichtigen Muster in den Daten vermissen; umgekehrt, wenn es hoch ist, kann es Kollisionen haben.
Die Auswahl guter Hyperparameter bietet zwei Hauptvorteile:
- Effiziente Suche im gesamten Bereich möglicher Hyperparameter; und
- Einfachere Verwaltung einer großen Anzahl von Experimenten zur Hyperparameterabstimmung.
Hyperparameter lassen sich grob in 2 Kategorien einteilen:
1. Optimierer Hyperparameter,
2. Modellspezifische Hyperparameter
Sie beziehen sich mehr auf den Optimierungs- und Trainingsprozess.
1.1. Lernrate:
Wenn die Modelllernrate viel zu klein als die optimalen Werte ist, dauert es viel länger (Hunderte oder Tausende) von Epochen, um einen idealen Zustand zu erreichen. Wenn andererseits die Lernrate viel größer als der optimale Wert ist, würde sie den Idealzustand überschreiten und der Algorithmus konvergiert möglicherweise nicht. Eine angemessene Anfangslernrate = 0,001.
Wichtig um das zu berücksichtigen:
a) Das Modell wird Hunderte und Tausende von Parametern mit jeweils einer eigenen Fehlerkurve haben. B) Fehlerkurven sind keine sauberen U-Formen; Stattdessen neigen sie dazu, komplexere Formen mit lokalen Minima zu haben.
1.2. Mini-Losgröße:
Die Stapelgröße wirkt sich auf nicht triviale Weise auf den Ressourcenbedarf des Trainingsprozesses, die Geschwindigkeit und die Anzahl der Iterationen aus.
In der Vergangenheit gab es eine Debatte über ein stochastisches Training, bei dem Sie ein einzelnes Beispiel des Datensatzes an das Modell anpassen und anhand nur eines Beispiels einen Vorwärtsdurchlauf durchführen und den Fehler berechnen / backpropagate & Legen Sie angepasste Werte für alle Hyperparameter fest. Führen Sie dies dann für jedes Beispiel im Datensatz erneut aus.
Oder vielleicht besser, die gesamten Daten in den Trainingsschritt einzuspeisen und den Gradienten anhand des Fehlers zu berechnen, der durch Betrachten aller Beispiele im Datensatz erzeugt wird. Dies nennt man Batch-Training.
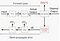
batch-Größe. Stochastisches Training ist, wenn die Minibatch-Größe = 1 ist, und Batch-Training ist, wenn die Mini-Batch-Größe = Anzahl der Beispiele im Trainingssatz. Empfohlene Startwerte für Experimente: 1, 2, 4, 8, 16, 32, 64, 128, 256.
Eine größere Mini-Batch-Größe ermöglicht rechnerische Boosts, die die Matrixmultiplikation in den Trainingsberechnungen verwenden . Dies geht jedoch zu Lasten der Notwendigkeit von mehr Speicher für den Trainingsprozess. Eine kleinere Mini-Batch-Größe führt zu mehr Rauschen bei Fehlerberechnungen , was häufig nützlicher ist, um zu verhindern, dass der Trainingsprozess bei lokalen Minima anhält. Ein fairer Wert für Mini-Batch-Größe = 32.
Während der rechnerische Schub uns dazu treibt, die Mini-Batch-Größe zu erhöhen, ist dieser praktische algorithmische Vorteil ein Anreiz, sie tatsächlich kleiner zu machen.
1.3. Anzahl der Epochen:
Um die richtige Anzahl von Epochen für den Trainingsschritt auszuwählen, sollten wir auf den Validierungsfehler achten.
in intuitiver manueller Weg besteht darin, das Modell für so viele Iterationen trainieren zu lassen, wie der Validierungsfehler abnimmt.
Es gibt eine Technik, die verwendet werden kann, genannt Early Stopping, um zu bestimmen, wann das Training des Modells beendet werden soll; Es geht darum, den Trainingsprozess zu stoppen, falls sich der Validierungsfehler in den letzten 10 oder 20 Epochen nicht verbessert hat.
2. Modellhyperparameter
Sie sind stärker an der Struktur des Modells beteiligt:
2.1. Anzahl versteckter Einheiten:
Die Anzahl versteckter Einheiten ist einer der mysteriöseren Hyperparameter. Denken wir daran, dass neuronale Netze universelle Funktionsannäherungen sind, und damit sie lernen können, eine Funktion (oder eine Vorhersageaufgabe) zu approximieren, müssen sie über genügend Kapazität verfügen, um die Funktion zu lernen. Die Anzahl der versteckten Einheiten ist das Hauptindikator für die Lernfähigkeit des Modells.
Für eine einfache Funktion benötigt sie möglicherweise weniger versteckte Einheiten. Je komplexer die Funktion, desto mehr Lernkapazität benötigt das Modell.
Eine etwas größere Anzahl von Einheiten als die optimale Anzahl ist kein Problem, aber eine viel größere Anzahl führt zu einer Überanpassung (dh wenn Sie ein Modell mit zu viel Kapazität bereitstellen, neigt es möglicherweise zu einer Überanpassung und versucht, den Datensatz zu „speichern“, wodurch die Verallgemeinerungsfähigkeit beeinträchtigt wird)
2.2. Erste versteckte Ebene:
Eine weitere Heuristik, die die erste versteckte Ebene betrifft, besteht darin, dass die Einstellung der Anzahl der versteckten Einheiten größer als die Anzahl der Eingaben tendenziell bessere Ergebnisse bei der Anzahl der Aufgaben ermöglicht, so die empirische Beobachtung.
2.3. Anzahl der Schichten:
Es ist oft der Fall, dass ein 3-lagiges neuronales Netz ein 2-lagiges Netz übertrifft. Aber noch tiefer zu gehen hilft selten viel mehr. (Ausnahme sind faltungsneurale Netze, bei denen je tiefer sie sind, desto besser sind sie).
Hyperparameter-Optimierungstechniken
Der Prozess des Findens optimaler Hyperparameter im maschinellen Lernen wird als Hyperparameter-Optimierung bezeichnet.
Gängige Algorithmen sind:
- Gittersuche
- Zufallssuche
- Bayes-Optimierung
Gittersuche
Die Gittersuche ist eine traditionelle Technik zur Implementierung von Hyperparametern. Es ist etwas über Brute-Force alle Kombinationen. Rastersuche erfordert creatingtwo Satz von Hyperparametern:
- Lernrate
- Anzahl der Ebenen
Grid search trainiert den Algorithmus für alle Kombinationen unter Verwendung der beiden Hyperparameter (Lernrate und Anzahl der Ebenen) und misst die Leistung mithilfe der Kreuzvalidierungstechnik. Diese Validierungstechnik stellt sicher, dass das trainierte Modell die meisten Muster aus dem Datensatz erhält (eine der besten Methoden zur Validierung ist die „K-fache Kreuzvalidierung“, die dazu beiträgt, ausreichend Daten für das Training des Modells und ausreichend Daten für Validierungen bereitzustellen).
Die Gittersuchmethode ist ein einfacherer Algorithmus, der jedoch leidet, wenn Daten einen hochdimensionalen Raum haben, der als Fluch der Dimensionalität bezeichnet wird.
Zufallssuche
Stichproben zufällig den Suchraum und wertet Mengen aus einer bestimmten Wahrscheinlichkeitsverteilung. Anstatt beispielsweise zu versuchen, alle 100.000 Stichproben zu überprüfen, können wir 1.000 zufällige Parameter überprüfen.
Der Nachteil des Zufallssuchalgorithmus besteht jedoch darin, dass er keine Informationen aus früheren Experimenten verwendet, um den nächsten Satz auszuwählen. Darüber hinaus ist es schwierig, die nächsten Experimente vorherzusagen.

Bayes’sche Optimierung
Die Hyperparametereinstellung maximiert die Leistung des Modells in einem Validierungssatz. ML-Algos erfordern häufig eine Feinabstimmung der Modellhyperparameter. Leider wird diese Funktion oft als ’schwarze Funktion‘ bezeichnet, da sie nicht in eine Formel geschrieben werden kann (Ableitungen der Funktion sind unbekannt).
Eine attraktivere Möglichkeit, & die Feinabstimmung von Hyperparametern zu optimieren, besteht darin, einen automatisierten Modellabstimmungsansatz zu ermöglichen – beispielsweise durch Verwendung der Bayes—Optimierung. Das Modell, das zur Approximation der Zielfunktion verwendet wird, wird als Ersatzmodell bezeichnet. Ein beliebtes Ersatzmodell für die Bayessche Optimierung ist der Gaußsche Prozess (GP). Die Bayes-Optimierung funktioniert typischerweise unter der Annahme, dass die unbekannte Funktion aus einem Gaußschen Prozess (GP) abgetastet wurde und eine posteriore Verteilung für diese Funktion beibehält, wenn Beobachtungen gemacht werden.
Bei der Bayes’schen Optimierung sind zwei wichtige Entscheidungen zu treffen:
- Wählen Sie Prior-Over-Funktionen aus, die Annahmen über die zu optimierende Funktion ausdrücken. Dazu wählen wir Gaußschen Prozess vor;
- Als nächstes müssen wir eine Akquisitionsfunktion wählen, die verwendet wird, um eine Utility-Funktion aus dem Modell posterior zu konstruieren, so dass wir den nächsten zu bewertenden Punkt bestimmen können.
Gaußscher Prozess
Ein Gaußscher Prozess definiert die vorherige Verteilung über Funktionen, die in eine posteriore Verteilung über Funktionen umgewandelt werden kann, sobald wir einige Daten gesehen haben. Der Gaußsche Prozess verwendet eine Kovarianzmatrix, um sicherzustellen, dass Werte nahe beieinander liegen. Die Kovarianzmatrix definiert zusammen mit einer mittleren µ-Funktion zur Ausgabe des Erwartungswertes ƒ(x) einen Gaußschen Prozess.
1. Der Gaußsche Prozess wird als Prior für die Bayes’sche Inferenz verwendet;
2. Die Berechnung der Daten ermöglicht es, Vorhersagen für unsichtbare Testfälle zu treffen.

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. Beliebte Erfassungsfunktionen sind
- Maximale Verbesserungswahrscheinlichkeit (MPI)
- Erwartete Verbesserung (EI)
- Obere Konfidenzgrenze (UCB)
Die erwartete Verbesserung (EI) ist beliebt und definiert als:
EI(x)=𝔼
wobei ƒ(x ) der aktuelle optimale Satz von Hyperparametern ist. Die Maximierung der Hyperparameter verbessert die Leistung.
