Unbeaufsichtigte Bayes-Inferenz (Reduzierung von Dimensionen und Freilegung von Features)
Low-Level-Feature-Erkennung mit Kanten

Endlich, der Moment, auf den Sie alle gewartet haben, der nächste in unserer unbeaufsichtigten Bayes-Inferenz-Serie: Unser (nicht so) tiefer Einblick in den Sobel-Operator.
Ein wirklich magischer Kantenerkennungsalgorithmus, der eine Low-Level-Feature-Extraktion und Dimensionsreduktion ermöglicht und das Rauschen im Bild wesentlich reduziert. Es war besonders nützlich bei Gesichtserkennungsanwendungen.Als Liebeskind von Irwin Sobel und Gary Feldman (Stanford Artificial Intelligence Laboratory) aus dem Jahr 1968 war dieser Algorithmus die Inspiration für viele moderne Kantenerkennungstechniken. Indem man zwei gegenüberliegende Kernel oder Masken über ein gegebenes Bild faltet (z.B. siehe unten-links) (jeweils in der Lage, entweder horizontale oder vertikale Kanten zu erkennen), können wir eine weniger verrauschte, geglättete Darstellung erstellen (siehe unten-rechts).
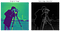
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel werte (normalerweise Luminanz) durch Differenzierung der Differenz zwischen jedem Pixel (dem Ankerpixel) und seinen umgebenden Pixeln (im Wesentlichen Annäherung an die Ableitung eines Bildes).
Dies führt dazu, dass das Originalbild geglättet wird und eine Ausgabe mit niedrigeren Abmessungen erzeugt wird, bei der geometrische Merkmale auf niedriger Ebene deutlicher sichtbar sind. Diese Ausgaben können dann als Eingaben in komplexere Klassifizierungsalgorithmen oder als Beispiele für unbeaufsichtigtes probabilistisches Clustering über Kullback-Leibler-Divergenz (KLD) verwendet werden (wie in meinem kürzlich erschienenen Blog über LBP zu sehen).
Um unsere Ausgabe mit niedrigeren Dimensionen zu generieren, müssen wir die Ableitung des Bildes vornehmen. Zuerst berechnen wir das Derivat in x- und y-Richtung. Wir erstellen zwei 3×3-Kernel (siehe Matrizen) mit Nullen entlang der Mitte der entsprechenden Achse, zwei in den mittleren Quadraten senkrecht zur zentralen Null und Einsen in jeder der Ecken. Jeder der Werte ungleich Null sollte oben / rechts von den Nullen (abhängig von der Achse) positiv und auf der entsprechenden Seite negativ sein. Diese Kernel heißen Gx und Gy.
Diese erscheinen im Format:
Diese Kernel werden dann über unser Bild gefaltet und platzieren das zentrale Pixel jedes Kernels über jedem Pixel im Bild. Wir verwenden die Matrixmultiplikation, um den Intensitätswert eines neuen entsprechenden Pixels in einem Ausgabebild für jeden Kernel zu berechnen. Daher erhalten wir zwei Ausgabebilder (eines für jede kartesische Richtung).
Ziel ist es, die Differenz / Änderung zwischen dem Pixel im Bild und allen Pixeln in der Gradientenmatrix (Kernel) (Gx und Gy) zu finden. Mathematisch kann dies ausgedrückt werden als.
Randnotiz:
Wir falten technisch nichts. Obwohl wir uns in KI- und maschinellen Lernkreisen gerne auf ‚Faltungen‘ beziehen, würde eine Faltung das Umdrehen des Originalbildes beinhalten. Wenn wir uns mathematisch auf Faltungen beziehen, berechnen wir wirklich die Kreuzkorrelation zwischen jedem 3×3-Bereich der Eingabe und der Maske für jedes Pixel. Das Ausgabebild ist die Gesamtkovarianz zwischen der Maske und der Eingabe. So werden die Kanten erkannt.
Zurück zu unserer Sobel-Erklärung…
Die berechneten Werte für jede Matrixmultiplikation zwischen der Maske und dem 3×3-Abschnitt der Eingabe werden summiert, um den endgültigen Wert für das Pixel im Ausgabebild zu erhalten. Dadurch wird ein neues Bild generiert, das Informationen über das Vorhandensein vertikaler und horizontaler Kanten im Originalbild enthält. Dies ist eine geometrische Merkmalsdarstellung des Originalbildes. Da dieser Bediener garantiert jedes Mal die gleiche Ausgabe erzeugt, ermöglicht diese Technik eine stabile Kantenerkennung für Bildsegmentierungsaufgaben.
Aus diesen Ausgaben können wir sowohl die Gradientengröße als auch die Gradientenrichtung (unter Verwendung des Arkustangens-Operators) bei jedem gegebenen Pixel (x, y) berechnen:
Daraus können wir feststellen, dass diese pixel mit großen Größen sind eher eine Kante im Bild, während die Richtung uns über die Kantenausrichtung informiert (obwohl die Richtung für die Erzeugung unserer Ausgabe nicht benötigt wird).
Eine einfache Implementierung:
Hier ist eine einfache Implementierung des Sobel-Operators in Python (mit NumPy), um Ihnen ein Gefühl für den Prozess zu geben (für alle angehenden Programmierer da draußen).
Diese Implementierung ist eine Python-Variante des Wikipedia-Pseudocode-Beispiels, mit dem Ziel zu zeigen, wie Sie diesen Algorithmus implementieren können, und gleichzeitig die verschiedenen Schritte im Prozess zu demonstrieren.
Warum interessiert uns das?
Obwohl die von diesem Operator erzeugte Gradientenannäherung relativ grob ist, bietet sie eine äußerst recheneffiziente Methode zur Berechnung von Kanten, Ecken und anderen geometrischen Merkmalen von Bildern. Im Gegenzug hat es den Weg für eine Reihe von Dimensionalitätsreduktions- und Merkmalsextraktionstechniken geebnet, wie z. B. lokale Binärmuster (weitere Informationen zu dieser Technik finden Sie in meinem anderen Blog).
Wenn Sie sich ausschließlich auf geometrische Merkmale verlassen, besteht die Gefahr, dass wichtige Informationen während der Codierung unserer Daten verloren gehen. Daher ist diese Technik besonders nützlich in Szenarien, in denen Textur und geometrische Merkmale bei der Definition der Eingabe als sehr wichtig angesehen werden können. Aus diesem Grund kann die Gesichtserkennung mit dem Sobel-Operator mit relativ hoher Genauigkeit durchgeführt werden. Diese Technik ist jedoch möglicherweise nicht die beste Wahl, wenn versucht wird, Eingaben zu klassifizieren oder zu gruppieren, die Farbe als Hauptunterscheidungsfaktor verwenden.
Diese Methode ist immer noch äußerst effektiv, um eine niedrigdimensionale Darstellung geometrischer Merkmale zu erhalten, und ein ausgezeichneter Ausgangspunkt für Dimensionalität und Rauschunterdrückung, bevor andere Klassifikatoren verwendet oder in Bayes-Inferenzmethoden verwendet werden.