
Ein künstliches neuronales Netzwerk (ANN) besteht aus vielen miteinander verbundenen Neuronen:
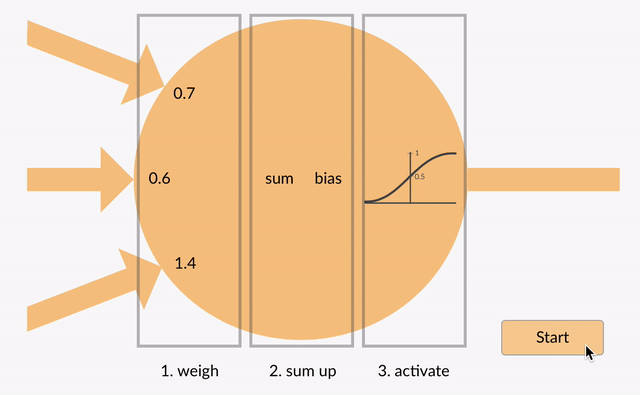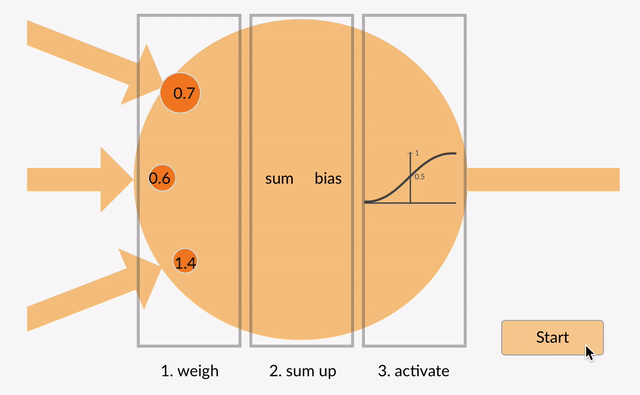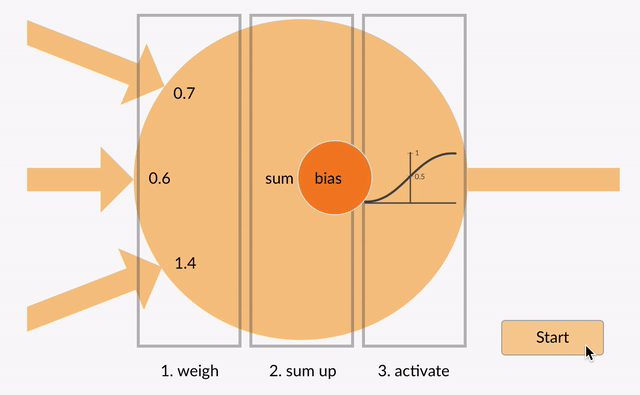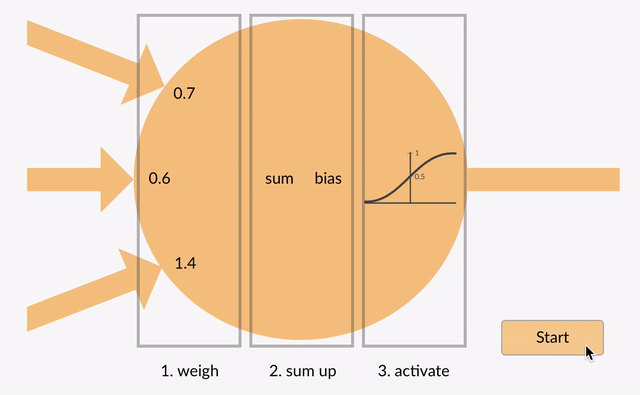
Jedes Neuron nimmt einige Gleitkommazahlen (z. B. 1,0, 0,5, -1.0) und multipliziert sie mit einigen anderen Gleitkommazahlen (z. B. 0,7, 0,6, 1,4), die als Gewichte bezeichnet werden (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Die Gewichte fungieren als Mechanismus, um bestimmte Eingaben zu fokussieren oder zu ignorieren.

Die gewichteten Eingaben werden dann summiert (z. 0.7 + 0.3 + -1.4 = -0.4) zusammen mit einem Bias-Wert (z.B. -0,4 + -0,1 = -0,5).
Der summierte Wert (x) wird nun entsprechend der Aktivierungsfunktion des Neurons (y = f(x)) in einen Ausgangswert (y) transformiert. Einige beliebte aktivierung funktionen sind unten dargestellt:

zB-0,5 →-0,05 wenn wir verwenden die Undichte Behoben Lineareinheit (Undichte ReLU) aktivierung funktion: y = f (x) = f (-0,5) = max (0,1 *-0,5,-0,5) = max (-0,05,-0,5) =-0.05
Der Ausgangswert des Neurons (z. B. -0,05) ist oft ein Eingang für ein anderes Neuron.
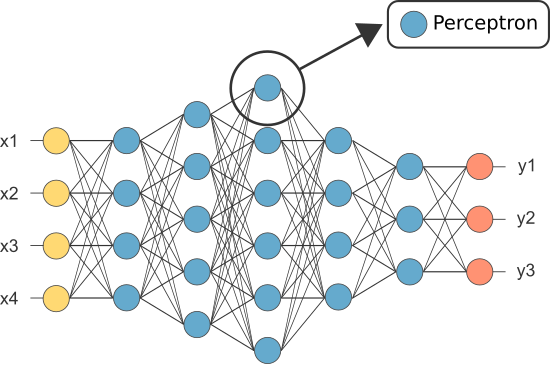
Eines der ersten ANNs war jedoch als Perzeptron bekannt und bestand nur aus einem einzigen Neuron.

Die Ausgabe des (einzigen) Neurons des Perzeptrons dient als endgültige Vorhersage.

Wir kodieren unser eigenes Perzeptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Hinweis: Wir haben keinen Lernalgorithmus in unser obiges Beispiel aufgenommen — wir werden Lernalgorithmen in einem anderen Tutorial behandeln)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

Warum brauchen wir also so viele Neuronen in einem ANN, wenn eines ausreicht (als Klassifikator)?

Leider können einzelne Neuronen nur linear trennbare Daten klassifizieren.

Durch die Kombination von Neuronen kombinieren wir jedoch im Wesentlichen ihre Entscheidungsgrenzen. Daher ist ein aus vielen Neuronen zusammengesetztes ANN in der Lage, komplexe, nichtlineare Entscheidungsgrenzen zu lernen.

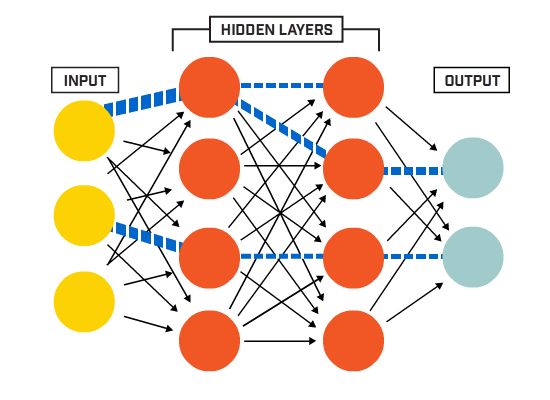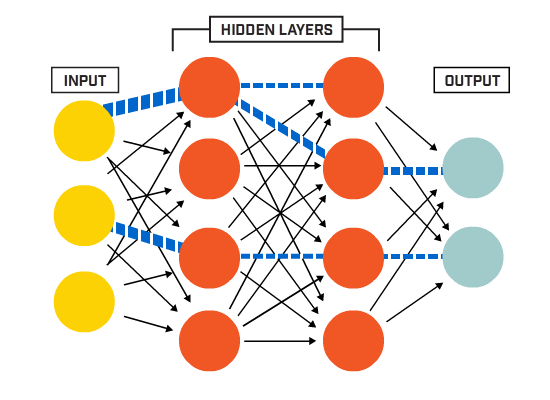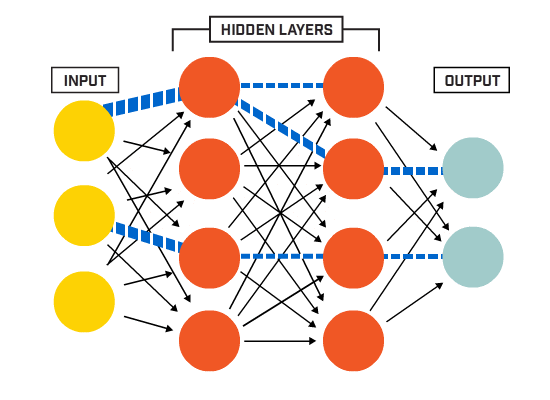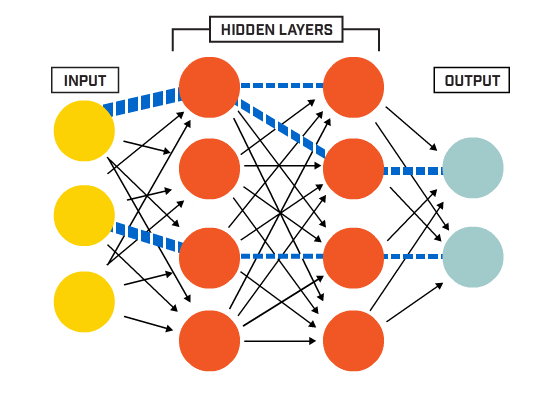
Neuronen sind gemäß einer bestimmten Netzwerkarchitektur miteinander verbunden. Obwohl es verschiedene Architekturen gibt, enthalten fast alle Schichten. (NB: Neuronen in der gleichen Schicht verbinden sich nicht miteinander)
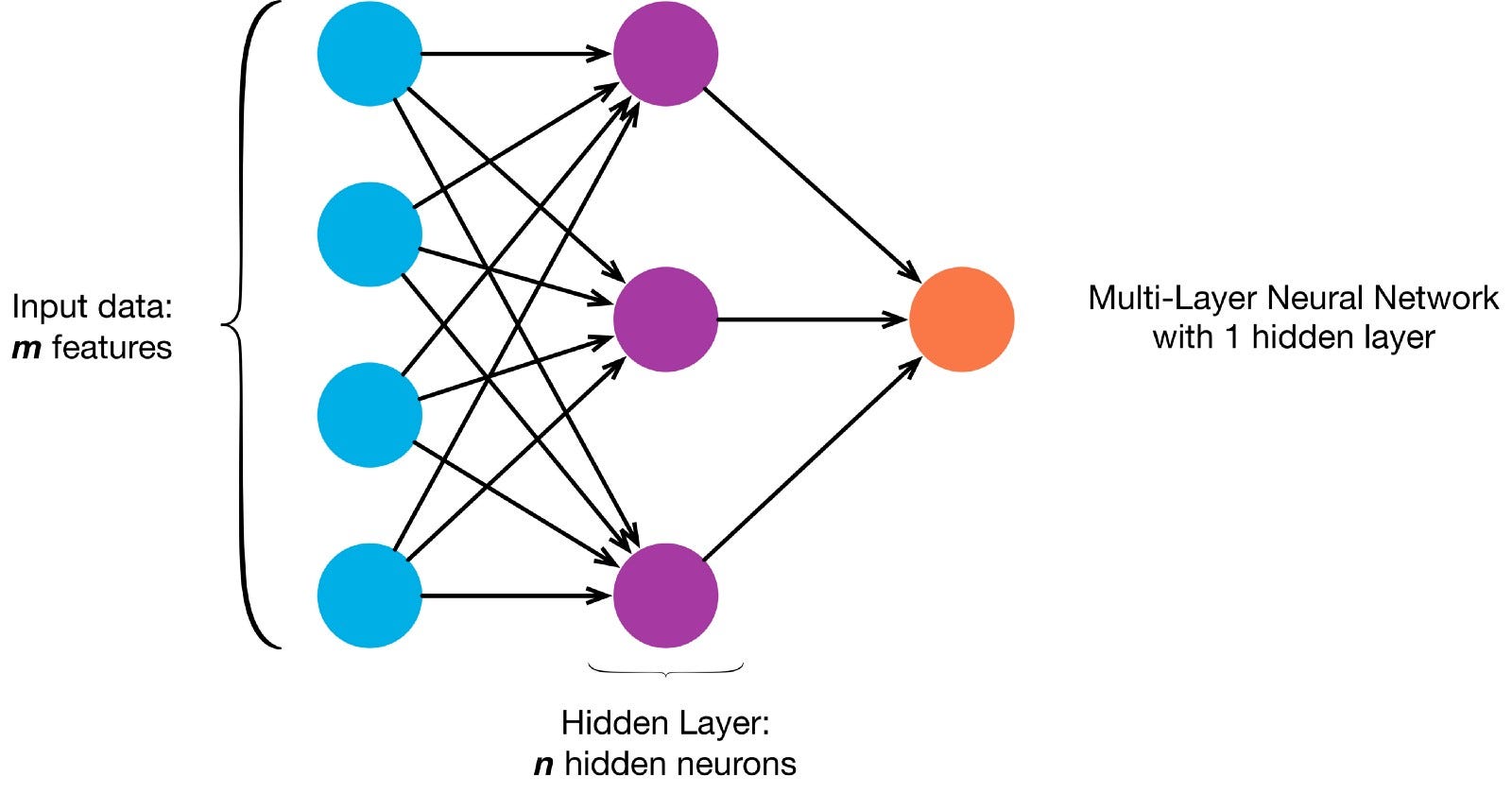
Es gibt typischerweise eine Eingangsschicht (die eine Anzahl von Neuronen enthält, die der Anzahl von Eingabemerkmalen in der die Daten), eine Ausgabeschicht (die eine Anzahl von Neuronen enthält, die der Anzahl der Klassen entspricht) und eine verborgene Schicht (die eine beliebige Anzahl von Neuronen enthält).

Es kann mehr als eine versteckte Schicht geben, damit das neuronale Netz komplexere Entscheidungsgrenzen lernen kann (Jedes neuronale Netz mit mehr als einer versteckten Schicht ist als ein tiefes neuronales Netz betrachtet).
Lass uns ein tiefes NN bauen, um dieses Bild zu malen:

Laden Sie das Bild herunter und laden Sie seine Pixel in ein array
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
Jetzt ist es eine überwachte Lernaufgabe, unseren Kindern das Malen beizubringen, daher müssen wir einen beschrifteten Trainingssatz erstellen (Unsere Trainingsdaten haben Eingaben und erwartete Ausgabebezeichnungen für jede Eingabe). Die Trainingseingaben haben 2 Werte (die x-, y-Koordinaten jedes Pixels).
Angesichts der Einfachheit des Bildes könnten wir dieses Problem auf zwei Arten angehen. Ein Klassifizierungsproblem (bei dem das neuronale Netz anhand seiner xy-Koordinaten vorhersagt, ob ein Pixel zur „blauen“ oder zur „grauen“ Klasse gehört) oder ein Regressionsproblem (bei dem das neuronale Netz RGB-Werte für ein Pixel anhand seiner Koordinaten vorhersagt).
Wenn Sie dies als Regressionsproblem behandeln: Die Trainingsausgaben haben 3 Werte (die normalisierten r-, g-, b-Werte für jedes Pixel). – Verwenden wir diese Methode vorerst.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Jetzt können wir unsere ANN erstellen:

- Es sollte 2 Neuronen in der Eingabeschicht haben (da 2 Werte zu berücksichtigen sind: x & y-Koordinaten).
- Es sollte 3 Neuronen in der Ausgabeschicht haben (da es 3 Werte zu lernen gibt: r, g, b).
- Die Anzahl der versteckten Schichten und die Anzahl der Neuronen in jeder versteckten Schicht sind zwei Hyperparameter, mit denen man experimentieren kann (sowie die Anzahl der Epochen, für die wir es trainieren werden, die Aktivierungsfunktion usw.) — ich werde 10 versteckte Schichten mit 100 Neuronen in jeder versteckten Schicht verwenden (was dies zu einem tiefen neuronalen Netzwerk macht)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
Das trainierte Netzwerk kann jetzt die normalisierten RGB-Werte für z. B. x, y = 1,1).
ann.predict(])
array(])
Mit dem ANN können Sie die RGB—Werte für jede Koordinate vorhersagen und die vorhergesagten RGB-Werte für das gesamte Bild anzeigen, um zu sehen, wie gut es funktioniert hat (qualitativ – wir werden Bewertungsmetriken für ein anderes Tutorial belassen)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

Versuchen Sie, die Hyperparameter zu ändern, um bessere Ergebnisse zu erzielen.
Wenn wir dies nicht als Regressionsproblem behandeln, sondern als Klassifizierungsproblem, haben die Trainingsausgaben 2 Werte (die Wahrscheinlichkeiten des Pixels, das zu jeder der beiden Klassen gehört: „blau“ und „grau“)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
Wir können unser ANN als binären Klassifikator mit 2 Neuronen in der Eingabeschicht, 2 Neuronen in der Ausgabeschicht und 100 Neuronen in der versteckten Schicht (mit 10 versteckten Schichten)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
Wir können jetzt die trainierte KLASSE verwenden, um die Klasse vorherzusagen, zu der jedes Pixel gehört (0: „grau“ oder 1: „blau“). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: „grey“)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

