Tutorial zum unbeaufsichtigten Lernen von Funktionen und Deep Learning

Einführung

Die Hauptkomponentenanalyse (PCA) ist ein Algorithmus zur Reduzierung der Dimensionalität, mit dem Sie Ihren Algorithmus zum Lernen von unbeaufsichtigten Funktionen erheblich beschleunigen können. Noch wichtiger ist, dass das Verständnis von PCA es uns ermöglicht, es später zu implementieren, was ein wichtiger Vorverarbeitungsschritt für viele Algorithmen ist.

Angenommen, Sie trainieren Ihren Algorithmus auf Bildern. Dann ist die Eingabe etwas redundant, da die Werte benachbarter Pixel in einem Bild stark korreliert sind. Nehmen wir konkret an, wir trainieren auf 16×16 Graustufenbildpatches. Dann sind \textstyle x\in \Re^{256} 256 dimensionale Vektoren, wobei ein Merkmal \textstyle x_j der Intensität jedes Pixels entspricht. Aufgrund der Korrelation zwischen benachbarten Pixeln können wir mit PCA die Eingabe mit einer viel niedrigeren Dimension annähern, während nur sehr wenige Fehler auftreten.

Beispiel und mathematischer Hintergrund

Für unser laufendes Beispiel verwenden wir einen Datensatz \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} mit \textstyle n=2 dimensionalen Eingaben, so dass \textstyle x^{(i)} \in \Re^2 . Angenommen, wir möchten die Daten von 2 Dimensionen auf 1 reduzieren. (In der Praxis möchten wir möglicherweise Daten von beispielsweise 256 auf 50 Dimensionen reduzieren. Aber die Verwendung von Daten mit niedrigeren Dimensionen in unserem Beispiel ermöglicht es uns, die Algorithmen besser zu visualisieren.) Hier ist unser Datensatz:

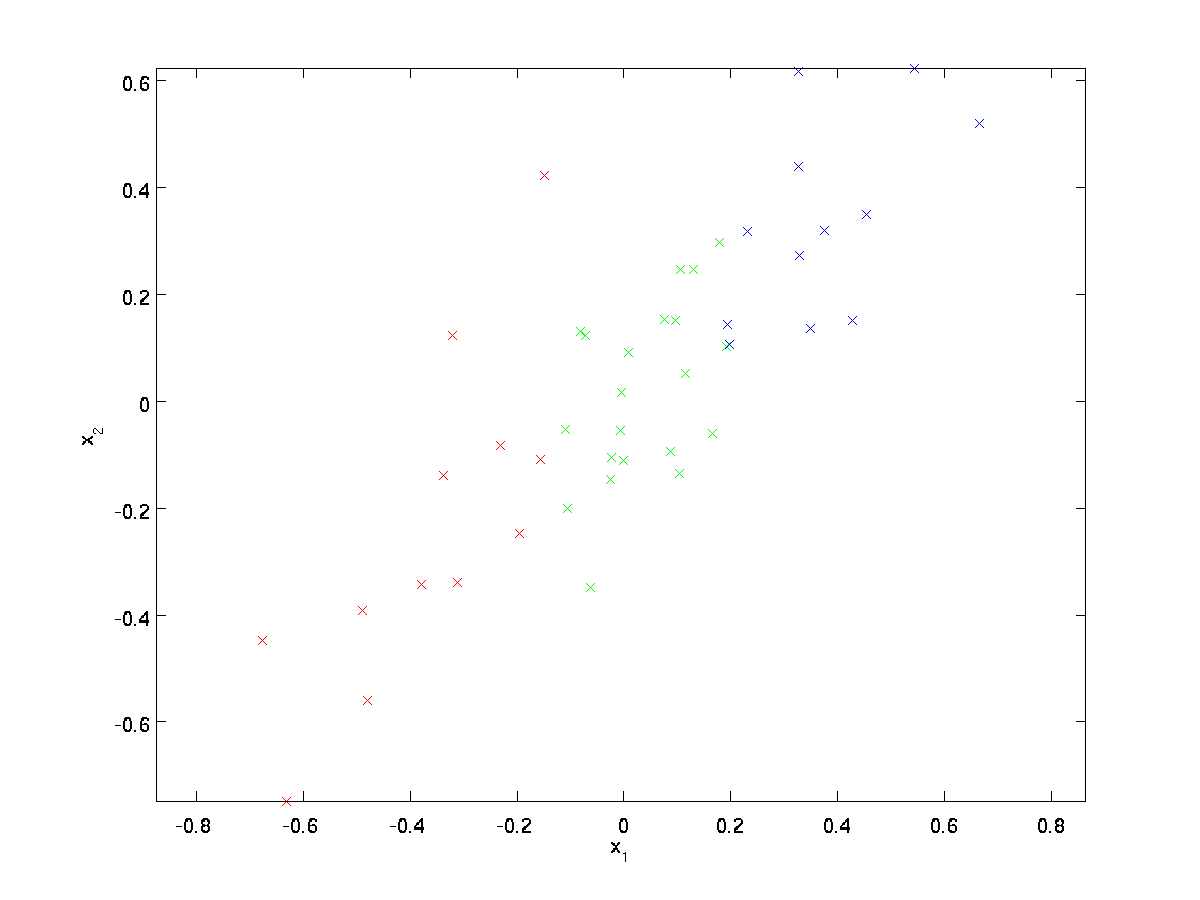
Diese Daten wurden bereits so vorverarbeitet, dass jedes der Merkmale \textstyle x_1 und \textstyle x_2 ungefähr den gleichen Mittelwert (Null) und die gleiche Varianz aufweist.

Zur Veranschaulichung haben wir auch jeden der Punkte eine von drei Farben gefärbt, abhängig von ihrem \textstyle x_1 Wert; diese Farben werden vom Algorithmus nicht verwendet und dienen nur zur Veranschaulichung.

PCA wird einen unterdimensionalen Unterraum finden, auf den wir unsere Daten projizieren können.
Aus der visuellen Untersuchung der Daten geht hervor, dass \textstyle u_1 die Hauptvariationsrichtung der Daten und \textstyle u_2 die sekundäre Variationsrichtung ist:

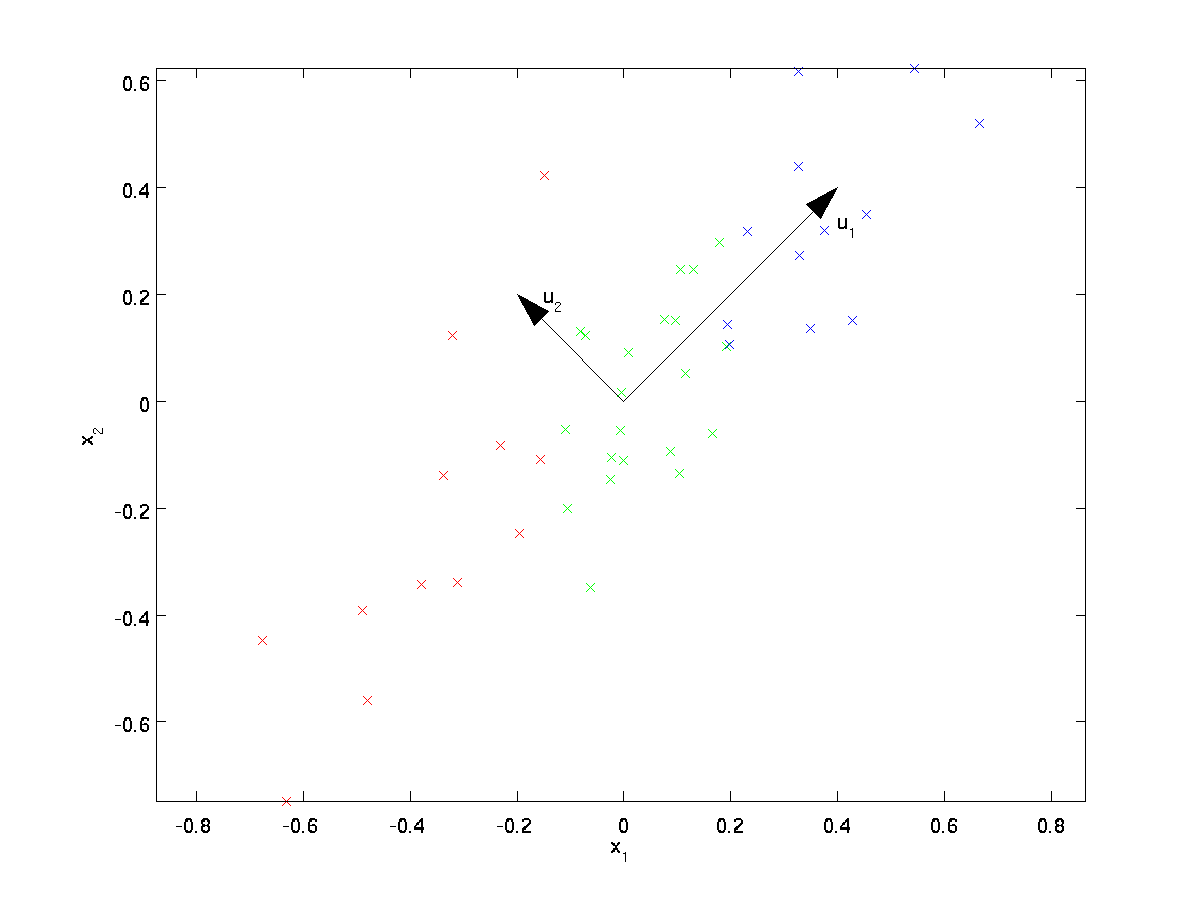
D. h. Die Daten variieren viel stärker in Richtung \textstyle u_1 als \textstyle u_2. Um die Richtungen \textstyle u_1 und \textstyle u_2 formeller zu finden, berechnen wir zuerst die Matrix \textstyle \Sigma wie folgt:

\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}

Wenn \textstyle x den Mittelwert Null hat, dann ist \textstyle \Sigma genau die Kovarianzmatrix von \textstyle x. (Das Symbol „\textstyle \Sigma“, ausgesprochen „Sigma“, ist die Standardnotation zur Bezeichnung der Kovarianzmatrix. Leider sieht es genauso aus wie das Summensymbol, wie in \sum_{i=1}^ni; aber das sind zwei verschiedene Dinge.)

Es kann dann gezeigt werden, dass \textstyle u_1 — die Hauptvariationsrichtung der Daten — der oberste (Haupt-) Eigenvektor von \textstyle \Sigma und \textstyle u_2 der zweite Eigenvektor ist.Hinweis: Wenn Sie an einer formaleren mathematischen Ableitung / Begründung dieses Ergebnisses interessiert sind, lesen Sie die CS229 (Machine Learning) Lecture Notes zu PCA (Link unten auf dieser Seite). Sie müssen dies jedoch nicht tun, um diesem Kurs zu folgen.

Sie können standardmäßige numerische lineare Algebra-Software verwenden, um diese Eigenvektoren zu finden (siehe Implementierungshinweise). Konkret berechnen wir die Eigenvektoren von \textstyle \Sigma und stapeln die Eigenvektoren in Spalten, um die Matrix \textstyle U zu bilden:

\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}

Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.

Die Vektoren \textstyle u_1 und \textstyle u_2 bilden in unserem Beispiel eine neue Basis, in der wir die Daten darstellen können. Konkret sei \textstyle x \in \Re^ 2 ein Trainingsbeispiel. Dann ist \textstyle u_1^Tx die Länge (magnitude) der Projektion von \textstyle x auf den Vektor \textstyle u_1.

In ähnlicher Weise ist \textstyle u_2^Tx die Größe von \textstyle x, die auf den Vektor \textstyle u_2 projiziert wird.

Drehen der Daten

Somit können wir \textstyle x auf der \textstyle (u_1, u_2)-Basis darstellen, indem wir

\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}

berechnen(Der Index „rot“ stammt aus der Beobachtung, dass dies einer Rotation (und möglicherweise Reflexion) der ursprünglichen Daten entspricht. Nehmen wir den gesamten Trainingssatz und berechnen \textstyle x_{\rm rot}^{(i)} = U^ Tx^{(i)} für jeden \textstyle i. Zeichnen wir diese transformierten Daten \textstyle x_{\rm rot} , erhalten wir:

Dies ist der Trainingssatz, der in die Basis \textstyle u_1,\textstyle u_2 gedreht wurde. Im Allgemeinen ist \textstyle U^Tx die Trainingsmenge, die in die Basis \textstyle u_1,\textstyle u_2, …,\textstyle u_n gedreht wird.

Eine der Eigenschaften von \textstyle U ist, dass es sich um eine „orthogonale“ Matrix handelt, was bedeutet, dass sie \textstyle U^TU = UU^T = I erfüllt. Wenn Sie also jemals von den gedrehten Vektoren \textstyle x_{\rm rot} zurück zu den ursprünglichen Daten \textstyle x müssen, können Sie berechnen

\begin{align}x = U x_{\rm rot} ,\end{align}

weil \textstyle U x_{\rm rot} = UU^T x = x.

Reduzieren der Datendimension

Wir sehen, dass die Hauptvariationsrichtung der Daten die erste Dimension \textstyle x_{\rm rot,1} dieser gedrehten Daten. Wenn wir also diese Daten auf eine Dimension reduzieren wollen, können wir

\begin{align}\tilde{x}^{(i)} = x_{\rm },1}^{(i)} = u_1^Tx^{(i)} \in \Re .\end{align}

Allgemeiner, wenn \textstyle x \in \Re^n und wir es auf eine \textstyle k Dimensionsdarstellung \textstyle \tilde{x} \in \Re^k reduzieren wollen (wobei k < n ), würden wir die ersten \textstyle k Komponenten von \textstyle x_{\rm_} , die den oberen \textstyle k Variationsrichtungen entsprechen.

Eine andere Möglichkeit, PCA zu erklären, ist, dass \textstyle x_{\rm_} ein \textstyle n dimensionaler Vektor ist, wobei die ersten Komponenten wahrscheinlich groß sind (z. in unserem Beispiel haben wir gesehen, dass \textstyle x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} für die meisten Beispiele relativ große Werte annimmt \textstyle i), und die späteren Komponenten sind wahrscheinlich klein (zB in unserem Beispiel war \textstyle x_{\rm rot,2}^{(i)} = u_2^Tx^{(i)} eher klein). Was PCA macht, ist, dass es die späteren (kleineren) Komponenten von \textstyle x_{\rm rot} fallen lässt und sie nur mit 0 annähert. Konkret kann unsere Definition von \textstyle \tilde{x} auch durch eine Annäherung an \textstyle x_{\rm rot} wobei alle außer den ersten \textstyle k Komponenten Nullen sind. Mit anderen Worten, wir haben:

\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\\ \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,k+1} \\\vdots \\ x_{\rm rot,n} \end{bmatrix}= x_{\rm rot} \end{align}

In unserem Beispiel ergibt dies den folgenden Plot von \textstyle \tilde{x} (mit \textstyle n=2, k=1):

Da jedoch die endgültigen \textstyle n-k Komponenten von \textstyle \tilde{x} wie oben definiert immer Null wären, müssen diese Nullen nicht beibehalten werden, und so definieren wir \textstyle \tilde{x} als \textstyle k-dimensionalen Vektor mit nur den ersten \textstyle k (ungleich Null) Komponenten.

Dies erklärt auch, warum wir unsere Daten in der \textstyle u_1, u_2, \ldots, u_n-Basis ausdrücken wollten: Die Entscheidung, welche Komponenten beibehalten werden sollen, wird nur die obersten \textstyle k-Komponenten beibehalten. Wenn wir dies tun, sagen wir auch, dass wir „die top \textstyle k PCA (oder principal) Komponenten beibehalten.“

Wiederherstellen einer Approximation der Daten

Nun ist \textstyle \tilde{x} \in \Re^k eine niederdimensionale, „komprimierte“ Darstellung des ursprünglichen \textstyle x \in \Re^n. Wie können wir angesichts von \textstyle \tilde{x} eine Approximation \textstyle \hat{x} an den ursprünglichen Wert von \textstyle x wiederherstellen? Aus einem früheren Abschnitt wissen wir, dass \textstyle x = U x_{\rm rot} . Außerdem können wir uns \textstyle \tilde{x} als eine Annäherung an \textstyle x_{\rm_} , wo wir die letzten \textstyle n-k Komponenten auf Nullen gesetzt haben. Wenn wir also \textstyle \tilde{x} \in \Re^k , können wir es mit \textstyle n-k Nullen auffüllen, um unsere Annäherung an \textstyle x_{\rmatrix} \in \Re^n . Schließlich multiplizieren wir mit \textstyle U , um unsere Annäherung an \textstyle x . Konkret erhalten wir

\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x} _k \\ 0 \\ \vdots \\ 0 \Ende{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}

Die obige endgültige Gleichheit ergibt sich aus der zuvor angegebenen Definition von \textstyle U. (In einer praktischen Implementierung würden wir \textstyle \tilde{x} nicht auf Null setzen und dann mit \textstyle U multiplizieren, da dies bedeuten würde, viele Dinge mit Nullen zu multiplizieren; Stattdessen würden wir einfach \textstyle \tilde{x} \in \Re^k mit den ersten \textstyle k Spalten von \textstyle U multiplizieren, wie im obigen endgültigen Ausdruck. Wenn wir dies auf unseren Datensatz anwenden, erhalten wir den folgenden Plot für \textstyle \hat{x}:

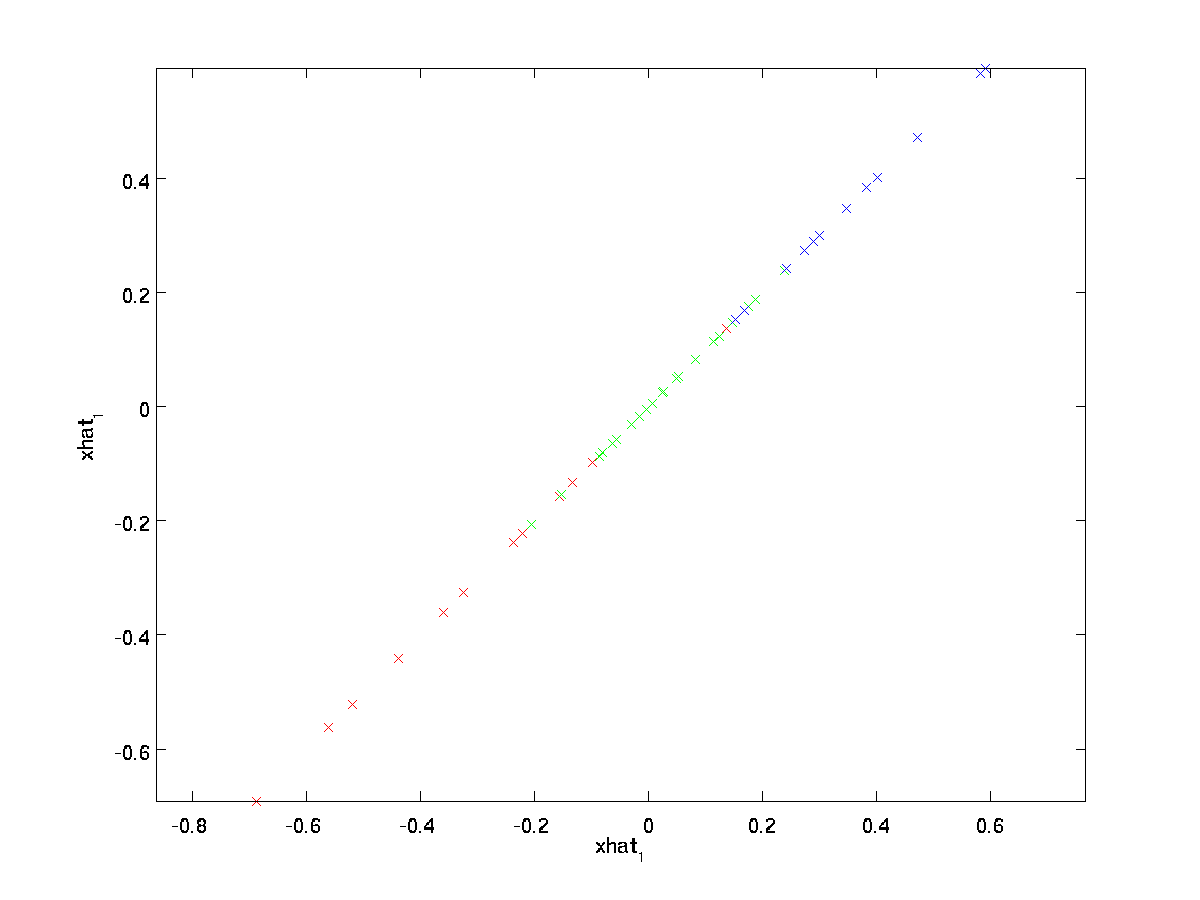
Wir verwenden also eine 1-dimensionale Annäherung an den ursprünglichen Datensatz.

Wenn Sie einen Autoencoder oder einen anderen unüberwachten Feature-Lernalgorithmus trainieren, hängt die Laufzeit Ihres Algorithmus von der Dimension der Eingabe ab. Wenn Sie \textstyle \tilde{x} \in \Re^k anstelle von \textstyle x in Ihren Lernalgorithmus \textstyle \tilde{x} \in \Re^k , trainieren Sie mit einer niedriger dimensionalen Eingabe, und Ihr Algorithmus wird möglicherweise erheblich schneller ausgeführt. Für viele Datensätze kann die niedrigdimensionale Darstellung von \textstyle \tilde{x} eine extrem gute Annäherung an das Original sein, und die Verwendung von PCA auf diese Weise kann Ihren Algorithmus erheblich beschleunigen und gleichzeitig einen sehr geringen Approximationsfehler verursachen.

Anzahl der zu behaltenden Komponenten

Wie setzen wir \textstyle k; d.h. wie viele PCA-Komponenten sollen wir behalten? In unserem einfachen 2-dimensionalen Beispiel schien es natürlich, 1 der 2 Komponenten beizubehalten, aber für höherdimensionale Daten ist diese Entscheidung weniger trivial. Wenn \textstyle k zu groß ist, werden wir die Daten nicht stark komprimieren; In der Grenze von \textstyle k=n verwenden wir nur die Originaldaten (aber auf eine andere Basis gedreht). Umgekehrt, wenn \textstyle k zu klein ist, verwenden wir möglicherweise eine sehr schlechte Annäherung an die Daten.

Um zu entscheiden, wie \textstyle k gesetzt wird, betrachten wir normalerweise den „‚Prozentsatz der Varianz beibehalten“‚ für verschiedene Werte von \textstyle k. Konkret, wenn \textstyle k=n , dann haben wir eine genaue Annäherung an die Daten, und wir sagen, dass 100% der Varianz beibehalten wird. I.e., alle Variationen der Originaldaten bleiben erhalten. Umgekehrt, wenn \textstyle k=0 ist, dann approximieren wir alle Daten mit dem Nullvektor, und somit bleibt 0% der Varianz erhalten.

Allgemeiner seien \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n die Eigenwerte von \textstyle \Sigma (in absteigender Reihenfolge sortiert), so dass \textstyle \lambda_j der Eigenwert ist, der dem Eigenvektor \textstyle u_j entspricht. Wenn wir dann \textstyle k Hauptkomponenten beibehalten, ist der Prozentsatz der beibehaltenen Varianz gegeben durch:

\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}.\end{align}

In unserem einfachen 2D-Beispiel oben ist \textstyle \lambda_1 = 7.29 und \textstyle \lambda_2 = 0.69. Indem wir also nur \textstyle k=1 Hauptkomponenten behalten, behalten wir \textstyle 7.29/(7.29+0.69) = 0.913, oder 91,3% der Varianz.

Eine formellere Definition des Prozentsatzes der beibehaltenen Varianz geht über den Rahmen dieser Anmerkungen hinaus. Es ist jedoch möglich zu zeigen, dass \textstyle \lambda_j =\sum_{i=1}^m x_{\rm},j}^2 . Wenn also \textstyle \lambda_j \approx 0 ist, zeigt dies, dass \textstyle x_{\rmx,j} normalerweise sowieso nahe 0 ist, und wir verlieren relativ wenig, wenn wir es mit einer konstanten 0 annähern. Dies erklärt auch, warum wir die oberen Hauptkomponenten (entsprechend den größeren Werten von \textstyle \lambda_j ) anstelle der unteren beibehalten. Die obersten Hauptkomponenten \textstyle x_ {\rm_,j} sind diejenigen, die variabler sind und größere Werte annehmen, und für die wir einen größeren Approximationsfehler erleiden würden, wenn wir sie auf Null setzen würden.

Im Falle von Bildern besteht eine übliche Heuristik darin, \textstyle k zu wählen, um 99% der Varianz beizubehalten. Mit anderen Worten, wir wählen den kleinsten Wert von \textstyle k , der

\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99 . \end{align}

Je nach Anwendung werden manchmal auch Werte im Bereich von 90-98% verwendet, wenn Sie bereit sind, zusätzliche Fehler zu verursachen. Wenn Sie anderen beschreiben, wie Sie PCA angewendet haben, ist die Aussage, dass Sie \textstyle k gewählt haben, um 95% der Varianz beizubehalten, auch eine viel leichter interpretierbare Beschreibung, als zu sagen, dass Sie 120 (oder eine andere Anzahl von) Komponenten beibehalten haben.

PCA auf Bildern

Damit PCA funktioniert, möchten wir normalerweise, dass jedes der Features \textstyle x_1, x_2, \ldots, x_n einen ähnlichen Wertebereich wie die anderen hat (und einen Mittelwert nahe Null hat). Wenn Sie PCA bereits in anderen Anwendungen verwendet haben, haben Sie daher möglicherweise jedes Feature separat vorverarbeitet, um den Mittelwert und die Einheitsvarianz von Null zu erhalten, indem Sie den Mittelwert und die Varianz jedes Features \textstyle x_j separat schätzen. Dies ist jedoch nicht die Vorverarbeitung, die wir auf die meisten Bildtypen anwenden werden. Angenommen, wir trainieren unseren Algorithmus mit „’natürlichen Bildern“‚, sodass \textstyle x_j der Wert von Pixel \textstyle j . Mit „natürlichen Bildern“ meinen wir informell die Art von Bild, die ein typisches Tier oder eine typische Person im Laufe ihres Lebens sehen könnte.

Hinweis: Normalerweise verwenden wir Bilder von Außenszenen mit Gras, Bäumen usw., und schneiden Sie kleine (sagen wir 16×16) Bildflecken zufällig aus diesen aus, um den Algorithmus zu trainieren. In der Praxis sind die meisten Feature-Learning-Algorithmen jedoch extrem robust gegenüber dem genauen Bildtyp, auf dem sie trainiert werden, sodass die meisten Bilder, die mit einer normalen Kamera aufgenommen wurden, funktionieren sollten, solange sie nicht übermäßig verschwommen sind oder seltsame Artefakte aufweisen.

Beim Training mit natürlichen Bildern ist es wenig sinnvoll, für jedes Pixel einen separaten Mittelwert und eine separate Varianz zu schätzen, da die Statistiken in einem Teil des Bildes (theoretisch) mit denen in anderen Teilen identisch sein sollten.
Diese Eigenschaft von Bildern wird als „‚Stationarität.“Damit PCA im Detail gut funktioniert, benötigen wir informell, dass (i) die Merkmale ungefähr den Mittelwert Null haben und (ii) die verschiedenen Merkmale ähnliche Varianzen zueinander aufweisen. Mit natürlichen Bildern ist (ii) auch ohne Varianznormalisierung bereits zufrieden, und so werden wir keine Varianznormalisierung durchführen.
(Wenn Sie auf Audiodaten trainieren-sagen wir, auf Spektrogramme-oder auf Textdaten-sagen wir, bag-of-Word-Vektoren-wir werden in der Regel nicht durchführen Varianznormalisierung entweder.)
Tatsächlich ist PCA für die Skalierung der Daten invariant und gibt unabhängig von der Skalierung der Eingabe dieselben Eigenvektoren zurück. Formal gesehen, wenn Sie jeden Merkmalsvektor \textstyle x mit einer positiven Zahl multiplizieren (also jedes Merkmal in jedem Trainingsbeispiel mit derselben Zahl skalieren), ändern sich die Ausgabe-Eigenvektoren von PCA nicht.

Wir werden also keine Varianznormalisierung verwenden. Die einzige Normalisierung, die wir dann durchführen müssen, ist die mittlere Normalisierung, um sicherzustellen, dass die Merkmale einen Mittelwert um Null haben. Je nach Anwendung interessiert uns sehr oft nicht, wie hell das gesamte Eingabebild ist. Bei Objekterkennungsaufgaben hat beispielsweise die Gesamthelligkeit des Bildes keinen Einfluss darauf, welche Objekte sich im Bild befinden. Formal sind wir nicht an dem mittleren Intensitätswert eines Bildflecks interessiert; Daher können wir diesen Wert als eine Form der mittleren Normalisierung herausziehen.

Wenn \textstyle x^{(i)} \in \Re^{n} die (Graustufen-) Intensitätswerte eines 16×16-Bildflecks sind (\textstyle n=256), können wir die Intensität jedes Bildes \textstyle x^{(i)} wie folgt normalisieren:

\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_jx^{(i )}_j := x^{(i)}_j – \mu^{(i)}

für alle \textstyle j

Beachten Sie, dass die beiden obigen Schritte für jedes Bild separat ausgeführt werden \textstyle x^{(i)}, und dass \textstyle \mu^{(i)} hier ist die mittlere Intensität des Bildes \textstyle x^{(i)}. Insbesondere ist dies nicht dasselbe wie das separate Schätzen eines Mittelwerts für jedes Pixel \textstyle x_j .

Wenn Sie Ihren Algorithmus auf anderen Bildern als natürlichen Bildern trainieren (z. B. Bildern von handgeschriebenen Zeichen oder Bildern einzelner isolierter Objekte, die vor einem weißen Hintergrund zentriert sind), können andere Arten der Normalisierung in Betracht gezogen werden, und die beste Wahl kann anwendungsabhängig sein. Beim Training mit natürlichen Bildern wäre jedoch die Verwendung der mittleren Normalisierungsmethode pro Bild, wie in den obigen Gleichungen angegeben, ein vernünftiger Standard.

Whitening

Wir haben PCA verwendet, um die Dimension der Daten zu reduzieren. Es gibt einen eng verwandten Vorverarbeitungsschritt namens Whitening (oder in einigen anderen Literaturen Sphering), der für einige Algorithmen benötigt wird. Wenn wir an Bildern trainieren, ist die Roheingabe redundant, da benachbarte Pixelwerte stark korreliert sind. Formal gesehen sind unsere Desideraten, dass unsere Lernalgorithmen eine Trainingseingabe sehen, bei der (i) die Merkmale weniger miteinander korrelieren und (ii) die Merkmale alle die gleiche Varianz aufweisen.

2D-Beispiel

Wir werden Whitening zunächst anhand unseres vorherigen 2D-Beispiels beschreiben. Wir werden dann beschreiben, wie dies mit Glättung kombiniert werden kann und schließlich, wie dies mit PCA kombiniert werden kann.

Wie können wir unsere Eingabefunktionen unkorreliert machen? Wir hatten dies bereits getan, als wir \textstyle x_ {\rmx}^{(i)} = U ^Tx^{(i)} berechneten.
Unsere vorherige Abbildung wiederholend, war unser Plot für \textstyle x_{\rmatrix}:

Die Kovarianzmatrix dieser Daten ist gegeben durch:

\begin{align}\begin{bmatrix}7.29 && 0.69\end{bmatrix}.\end{align}

(Hinweis: Technisch gesehen sind viele der Aussagen in diesem Abschnitt über die „Kovarianz“ nur dann wahr, wenn die Daten den Mittelwert Null haben. Im Rest dieses Abschnitts werden wir diese Annahme als implizit in unseren Aussagen annehmen. Selbst wenn der Mittelwert der Daten nicht genau Null ist, gelten die Intuitionen, die wir hier präsentieren, immer noch, und Sie sollten sich daher keine Sorgen machen.)

Es ist kein Zufall, dass die Diagonalwerte \textstyle \lambda_1 und \textstyle \lambda_2 sind. Ferner sind die Einträge außerhalb der Diagonale Null; somit sind \textstyle x_{\rm rot,1} und \textstyle x_{\rm rot,2} unkorreliert und erfüllen eine unserer Desideraten für weiße Daten (dass die Merkmale weniger korreliert sind).

Um sicherzustellen, dass jedes unserer Eingabe-Features eine Einheitsvarianz aufweist, können wir einfach jedes Feature \textstyle x_{\rm_,i} durch \textstyle 1/\sqrt{\lambda_i} neu skalieren. Konkret definieren wir unsere weißen Daten \textstyle x_{\rm PCAwhite} \in \Re^n wie folgt:

\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \end{align}

Plotten \textstyle x_{\rm PCAwhite}, erhalten wir:

Diese Daten haben jetzt eine Kovarianz gleich der Identitätsmatrix \textstyle I. Wir sagen, dass \textstyle x_{\rm PCAwhite} unsere PCA-weiße Version der Daten ist: Die verschiedenen Komponenten von \textstyle x_{\rm PCAwhite} sind unkorreliert und weisen eine Einheitsvarianz auf.

Whitening kombiniert mit Dimensionsreduktion. Wenn Sie Daten haben möchten, die weiß sind und eine niedrigere Dimension als die ursprüngliche Eingabe haben, können Sie optional auch nur die oberen \textstyle k-Komponenten von \textstyle x_{\rm PCAwhite} beibehalten. Wenn wir die PCA-Aufhellung mit der Regularisierung kombinieren (später beschrieben), sind die letzten Komponenten von \textstyle x_ {\rm PCAwhite} sowieso nahezu Null und können daher sicher gelöscht werden.

ZCA :

Schließlich stellt sich heraus, dass diese Art, die Daten mit der Kovarianzidentität \textstyle I zu versehen, nicht eindeutig ist. Konkret, wenn \textstyle R eine orthogonale Matrix ist, so dass sie \textstyle RR^T = R^ TR = I erfüllt (weniger formal, wenn \textstyle R eine Rotations- / Reflexionsmatrix ist), dann \textstyle R \,x_{\rm PCAwhite} wird auch Identitätskovarianz haben.

In ZCA whitening wählen wir \textstyle R = U. Wir definieren

\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}

Plotten \textstyle x_{\rm ZCAwhite}, wir bekommen:

Es kann gezeigt werden, dass aus allen möglichen auswahlmöglichkeiten für \textstyle R, diese Wahl der Drehung bewirkt, dass \textstyle x_{\rm ZCAwhite} so nah wie möglich an den ursprünglichen Eingabedaten \textstyle x .

Wenn wir ZCA whitening (im Gegensatz zu PCA whitening) verwenden, behalten wir normalerweise alle \textstyle n Dimensionen der Daten bei und versuchen nicht, ihre Dimension zu reduzieren.

Regularizaton

Bei der Implementierung von PCA whitening oder ZCA whitening in der Praxis sind manchmal einige der Eigenwerte \textstyle \lambda_i numerisch nahe 0, und daher würde der Skalierungsschritt, bei dem wir durch \sqrt{\lambda_i} dividieren, die Division durch einen Wert nahe Null beinhalten; Dies kann dazu führen, dass die Daten explodieren (große Werte annehmen) oder anderweitig numerisch instabil sind. In der Praxis implementieren wir diesen Skalierungsschritt daher mit einer kleinen Regularisierung und fügen den Eigenwerten eine kleine Konstante \textstyle \epsilon hinzu, bevor wir ihre Quadratwurzel und Inverse nehmen:

\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i + \epsilon}}.\end{align}

Wenn \textstyle x Werte um \textstyle annimmt, könnte ein Wert von \textstyle \epsilon \approx 10^{-5} typisch sein.

Für den Fall von Bildern hat das Hinzufügen von \textstyle \epsilon hier auch den Effekt, dass das Eingabebild leicht geglättet (oder tiefpassgefiltert) wird. Dies hat auch einen wünschenswerten Effekt des Entfernens von Aliasing-Artefakten, die durch die Art und Weise verursacht werden, wie Pixel in einem Bild angeordnet sind, und kann die erlernten Funktionen verbessern (Details gehen über den Rahmen dieser Hinweise hinaus).

ZCA Whitening ist eine Form der Vorverarbeitung der Daten, die sie von \textstyle x auf \textstyle x_{\rm ZCAwhite} . Es stellt sich heraus, dass dies auch ein grobes Modell dafür ist, wie das biologische Auge (die Netzhaut) Bilder verarbeitet. Wenn Ihr Auge Bilder wahrnimmt, nehmen die meisten benachbarten „Pixel“ in Ihrem Auge sehr ähnliche Werte wahr, da benachbarte Teile eines Bildes in der Intensität tendenziell stark korrelieren. Es ist daher verschwenderisch für Ihr Auge, jedes Pixel separat (über Ihren Sehnerv) an Ihr Gehirn übertragen zu müssen. Stattdessen führt Ihre Netzhaut eine Dekorrelationsoperation durch (dies geschieht über Netzhautneuronen, die eine Funktion namens „on center, off Surround / off center, on Surround“ berechnen), die der von ZCA durchgeführten ähnelt. Dies führt zu einer weniger redundanten Darstellung des Eingabebildes, das dann an Ihr Gehirn übertragen wird.

Implementieren von PCA Whitening

In diesem Abschnitt fassen wir die Algorithmen PCA, PCA Whitening und ZCA Whitening zusammen und beschreiben, wie Sie sie mithilfe effizienter linearer Algebra-Bibliotheken implementieren können.

Zuerst müssen wir sicherstellen, dass die Daten (ungefähr) einen Mittelwert von Null haben. Für natürliche Bilder erreichen wir dies (ungefähr), indem wir den Mittelwert jedes Bildflecks subtrahieren.

Wir erreichen dies, indem wir den Mittelwert für jeden Patch berechnen und für jeden Patch subtrahieren. In Matlab können wir dies tun, indem wir

 avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);

Als nächstes müssen wir \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T Wenn Sie dies in Matlab implementieren (oder auch wenn Sie dies in C ++, Java usw. implementieren)., aber Zugriff auf eine effiziente lineare Algebra-Bibliothek haben), ist es ineffizient, dies als explizite Summe zu tun. Stattdessen können wir dies auf einen Schlag berechnen als

 sigma = x * x' / size(x, 2);

(Überprüfen Sie die Mathematik selbst auf Richtigkeit.) Hier nehmen wir an, dass x eine Datenstruktur ist, die ein Trainingsbeispiel pro Spalte enthält (x ist also eine \textstyle n-by-\textstyle m Matrix).

Als nächstes berechnet PCA die Eigenvektoren von \Sigma. Man könnte dies mit der Matlab eig Funktion tun. Da \Sigma jedoch eine symmetrische positive halbdefinierte Matrix ist, ist es numerisch zuverlässiger, dies mit der svd-Funktion zu tun. Konkret, wenn Sie implementieren

 = svd(sigma);

dann enthält die Matrix U die Eigenvektoren von \Sigma (ein Eigenvektor pro Spalte, sortiert in der Reihenfolge von oben nach unten Eigenvektor), und die diagonalen Einträge der Matrix S enthalten die entsprechenden Eigenwerte (ebenfalls in absteigender Reihenfolge sortiert). Die Matrix V ist gleich U und kann sicher ignoriert werden.

(Hinweis: Die svd-Funktion berechnet tatsächlich die singulären Vektoren und singulären Werte einer Matrix, die für den Spezialfall einer symmetrischen positiven halbdefinierten Matrix – mit der wir uns hier befassen — gleich ihren Eigenvektoren und Eigenwerten ist. Eine vollständige Diskussion von singulären Vektoren vs. Eigenvektoren geht über den Rahmen dieser Hinweise hinaus.)

Schließlich können Sie \textstyle x_{\rmx} und \textstyle \tilde{x} wie folgt berechnen:

 xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keep

Dies gibt Ihrer PCA-Darstellung der Daten in Bezug auf \textstyle \tilde{x} \in \Re^k. Übrigens, wenn x eine \textstyle n-by-\textstyle m Matrix ist, die alle Ihre Trainingsdaten enthält, ist dies eine vektorisierte Implementierung, und die obigen Ausdrücke funktionieren auch für die Berechnung von x_{\rmx} und \tilde{x} für Ihre gesamte Trainingssatz auf einmal. Die resultierenden x_{\rm_} und \tilde{x} haben eine Spalte, die jedem Trainingsbeispiel entspricht.

Um die PCA-Weißdaten zu berechnen \textstyle x_{\rm PCAwhite}, verwenden Sie

 xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

Da die Diagonale von S die Eigenwerte \textstyle \lambda_i , erweist sich dies als eine kompakte Art der Berechnung \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{ \sqrt{\lambda_i}} gleichzeitig für alle \textstyle i.

Schließlich können Sie auch die ZCA-weißen Daten \textstyle x_{\rm ZCAwhite} wie folgt berechnen:

 xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;