Was ist ein ARIMAX-Modell?

Was ist das ARIMAX-Modell?

Wenn Sie unsere Reihe von Blog-Tutorials zu Modellen zur Schätzung von Zeitreihendaten gelesen haben, sind Sie bereits mit 3 Hauptansätzen vertraut – Autoregression, gleitende Durchschnitte und Integration.

Was ist das gemeinsame Thema in all diesen Modellen?

Sie beruhten ausschließlich auf einer einzigen Variablen.

Ein Modell kann jedoch auch mehr als nur vergangene Preise oder vergangene Residuen berücksichtigen.

Und dies sind die sogenannten „MAX“ -Modelle, wobei der ARMAX die nicht integrierte Version und der ARIMAX das integrierte Äquivalent ist.

In diesem Tutorial werden wir also untersuchen, wie sie aussehen, und Ihnen Schritt für Schritt zeigen, wie Sie sie in Python implementieren.

Lass uns anfangen, sollen wir?

Warum werden ARMAX und ARIMAX „MAX“-Modelle genannt?

Die Namen ARMAX und ARIMAX sind Erweiterungen von ARMA und ARIMA. Das X am Ende steht für „exogenous“. Mit anderen Worten, es wird vorgeschlagen, eine separate externe Variable hinzuzufügen, um unsere endogene Variable zu messen.

Die ARMAX- und ARIMAX-Modellgleichung:

Da der einzige Unterschied zwischen ARMAX und ARIMAX darin besteht, dass einer integriert ist und der andere nicht, können wir einen von ihnen untersuchen und dann hervorheben, wie sich der andere unterscheiden würde.

Wir haben in unserem letzten Blogartikel (ARIMA) ein integriertes Modell untersucht, also lasst uns sehen, wie die Gleichung des ARIMAX aussieht.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

Natürlich wäre die Gleichung für den ARMAX die gleiche, außer dass wir die tatsächliche Variable, sagen wir P , anstelle ihres Deltas verwenden würden.

Pt=c+ßX+ϕ1 Pt-1+ θ1 ϵt-1 +ϵt

Aufschlüsselung der ARIMAX-Gleichung:

Wir können uns den ARMAX als Sonderfall des ARIMAX vorstellen, wobei die Integrationsreihenfolge 0 ist.

Für den Rest des Tutorials konzentrieren wir uns also auf den ARIMAX.

Und wir beginnen damit, die verschiedenen Teile darin aufzuschlüsseln. Für den Anfang stellen Pt und Pt-1 die Werte in der aktuellen Periode bzw. vor 1 Periode dar.

In ähnlicher Weise sind ϵt und ϵt-1 die Fehlerterme für die gleichen zwei Perioden. Und natürlich ist c nur ein konstanter Basislinienfaktor.

Die beiden Parameter ϕ1 und θ1 drücken aus, welche Teile des Wertes Pt-1 und des Fehlers ϵt-1 letzte Periode für die Schätzung der aktuellen relevant sind.

Nun sind die beiden neuen Ergänzungen des Modells „X“ und sein Koeffizient β. Genau wie ϕ ist β ein Koeffizient, der basierend auf der Modellauswahl und den Daten geschätzt wird. Aber was ist mit X?

Was ist eine exogene Variable?

Nun, X ist die exogene Variable und es kann jede Variable sein, an der wir interessiert sind.

Es kann sich um eine zeitlich variierende Messung wie die Inflationsrate oder den Preis eines anderen Index handeln. Oder eine kategoriale Variable, die die verschiedenen Wochentage trennt. Es kann auch eine boolesche Buchhaltung für die besonderen Festtage sein. Schließlich kann es für eine Kombination mehrerer verschiedener externer Faktoren stehen.

Die Idee ist, dass es jede andere Variable oder Variablen sein kann, die die Preise beeinflussen können, solange wir die Daten zur Verfügung haben.

Solche äußeren Faktoren sind in unserer Regression als exogene Variablen bekannt. Wir verwenden ihre Werte, um diejenige vorherzusagen und zu erklären, an der wir interessiert sind, was in unserem Fall die aktuellen Preise sind.

Wie werden ARMAX- und ARIMAX-Modelle in Python implementiert?

Praktischerweise enthält das statsmodels-Paket eine Methode namens ARIMA, die solche zusätzlichen Eingaben vollständig verarbeiten kann.

Wir beginnen mit der Angabe der Modelleigenschaften und der Reihenfolge des Modells:

Nachdem wir das getan haben, müssen wir auch das exogene Argument „exog“ angeben.

Der Wert, den wir übergeben möchten, muss ein Array irgendeiner Art sein, da wir Werte mit jedem Zeitraum verknüpfen möchten.

Zum Beispiel können wir S&P Preise als diese exogene Variable verwenden, da wir sie bereits in unseren Daten haben.

Jetzt sind wir bereit, ein ARIMAX (1,1,1) -Modell zu montieren.

Stellen Sie sicher, dass Sie Ihre Modellvariable so benennen, dass sie sich von ähnlichen Modellen unterscheidet. In diesem Fall wählen wir dies, indem wir am Ende „X, spx“ hinzufügen, um anzuzeigen, dass die exogene Variable die S&P.

Dann setzen wir, wie aus den Snippets hervorgeht, diese gleich der ARIMA-Methode wie zuvor, fügen die Zeitreihen und die Reihenfolge hinzu, wie wir es gewohnt sind. Schließlich setzen wir zwischen den beiden das Argument „exog“ gleich „DF SPX“, was die S&P-Preise angibt.

Wenn wir dieses Modell anpassen und seine Übersichtstabelle drucken, werden wir sehen, dass wir eine zusätzliche Zeile für die S&P-Preise erhalten.

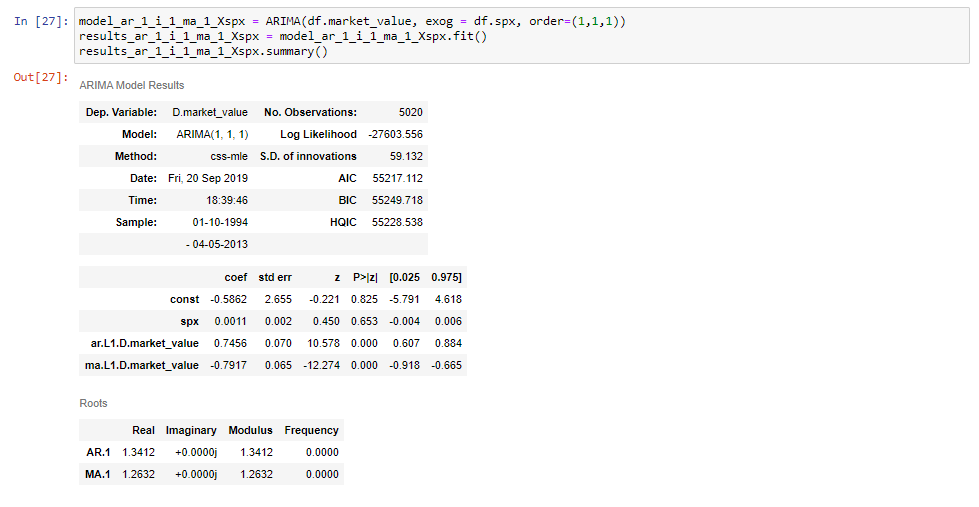
Und das ist alles!

Wir haben erfolgreich gesehen, wie man ein ARIMAX-Modell in Python implementiert.

Wenn Sie mehr über ARIMAX und andere Zeitreihenmodelle in Python erfahren möchten, lesen Sie unsere Schritt-für-Schritt-Python-Tutorials. Wenn Sie neu in Python sind und mehr darüber erfahren möchten, führt Sie dieser umfassende Artikel zum Erlernen der Python-Programmierung von der Installation über Python-IDEs, Bibliotheken und Frameworks bis hin zu den besten Python-Karrierewegen und Jobaussichten.

Bereit für den nächsten Schritt in Richtung Data Science?

Schauen Sie sich noch heute das komplette Data Science-Programm an. Beginnen Sie mit den Grundlagen unserer Statistik-, Mathematik- und Excel-Kurse. Erstellen Sie eine schrittweise Erfahrung mit SQL, Python, R, Power BI und Tableau. Erweitern Sie Ihre Fähigkeiten mit maschinellem Lernen, Deep Learning, Kreditrisikomodellierung, Zeitreihenanalyse und Kundenanalysen in Python. Sie sind sich immer noch nicht sicher, ob Sie Ihr Interesse an Data Science in eine Karriere verwandeln möchten? Sie können den Lehrplan erkunden oder sich kostenlos für 15 Stunden Videoinhalte für Anfänger bis Fortgeschrittene anmelden, indem Sie auf die Schaltfläche unten klicken.