Introduction
L’analyse en composantes principales (PCA) est un algorithme de réduction de la dimensionnalité qui peut être utilisé pour accélérer considérablement votre algorithme d’apprentissage des fonctionnalités non supervisé. Plus important encore, la compréhension de la PCA nous permettra de mettre en œuvre ultérieurement le blanchiment, qui est une étape de prétraitement importante pour de nombreux algorithmes.
Supposons que vous entraînez votre algorithme sur des images. Ensuite, l’entrée sera quelque peu redondante, car les valeurs des pixels adjacents dans une image sont fortement corrélées. Concrètement, supposons que nous nous entraînions sur des patchs d’image en niveaux de gris 16×16. Alors \textstyle x\in\Re^{256} sont des vecteurs dimensionnels 256, avec une caractéristique \textstyle x_j correspondant à l’intensité de chaque pixel. En raison de la corrélation entre les pixels adjacents, PCA nous permettra d’approximer l’entrée avec une dimension beaucoup plus faible, tout en encourant très peu d’erreurs.
Exemple et contexte mathématique
Pour notre exemple en cours d’exécution, nous utiliserons un ensemble de données \textstyle\{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} avec \textstyle n = 2 entrées dimensionnelles, de sorte que \textstyle x^{(i)}\in\Re^2. Supposons que nous souhaitions réduire les données de 2 dimensions à 1. (En pratique, nous pourrions vouloir réduire les données de 256 à 50 dimensions, par exemple; mais l’utilisation de données de dimensions inférieures dans notre exemple nous permet de mieux visualiser les algorithmes.) Voici notre jeu de données:
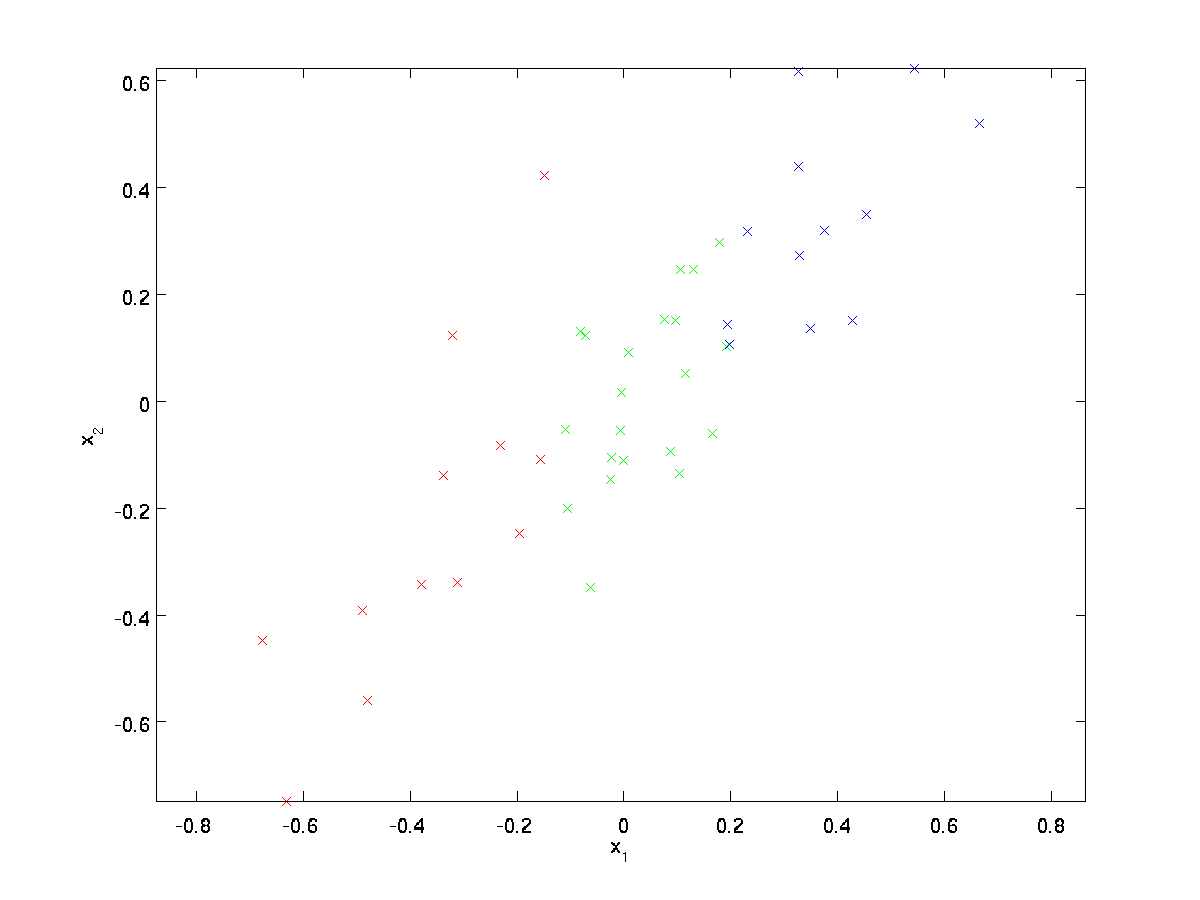
Ces données ont déjà été prétraitées afin que chacune des entités \textstyle x_1 et \textstyle x_2 ait à peu près la même moyenne (zéro) et la même variance.
À des fins d’illustration, nous avons également coloré chacun des points d’une des trois couleurs, en fonction de leur valeur \textstyle x_1; ces couleurs ne sont pas utilisées par l’algorithme, et sont uniquement à titre d’illustration.
PCA trouvera un sous-espace de dimension inférieure sur lequel projeter nos données.
En examinant visuellement les données, il apparaît que \textstyle u_1 est la direction principale de variation des données, et \textstyle u_2 la direction secondaire de variation:
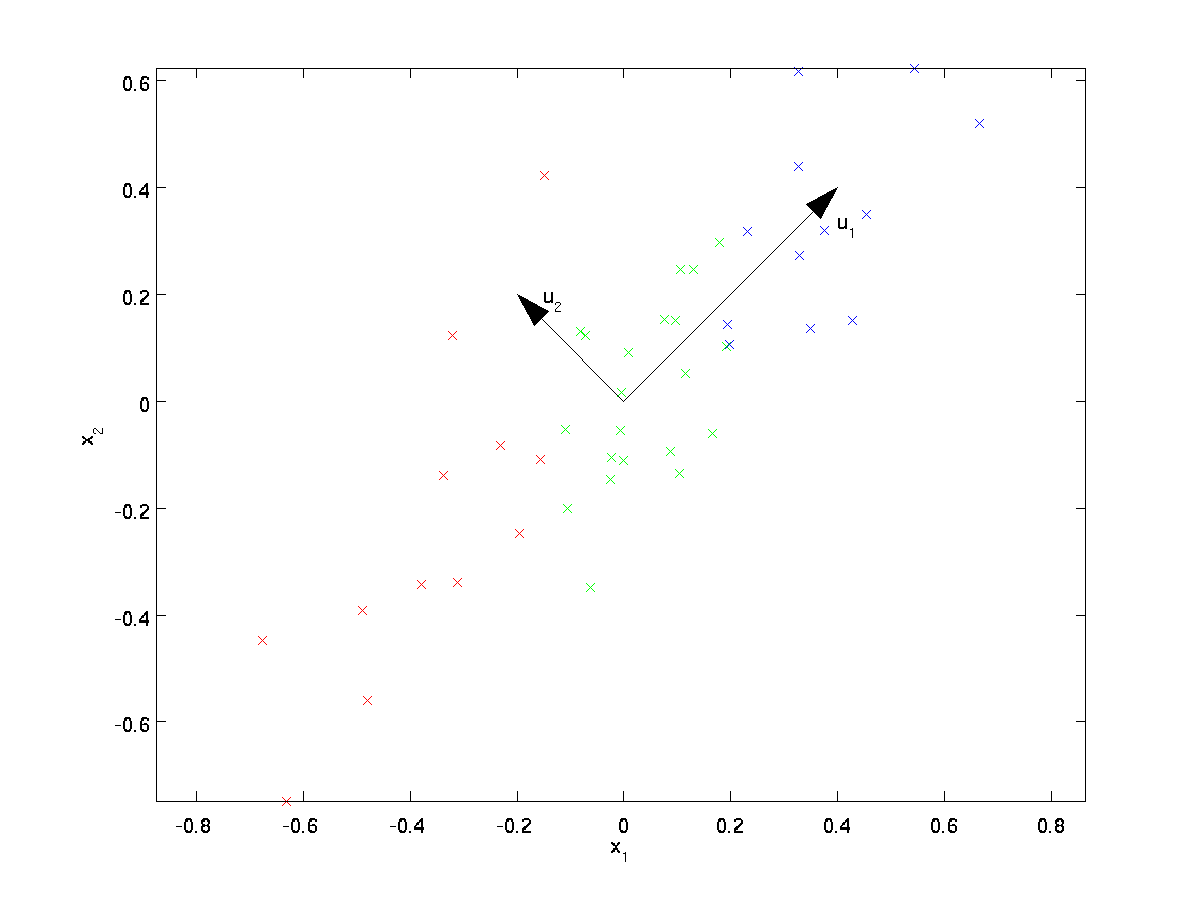
C’est-à-dire que les données varient beaucoup plus dans la direction \textstyle u_1 que \textstyle u_2. Pour trouver plus formellement les directions \textstyle u_1 et \textstyle u_2, nous calculons d’abord la matrice \textstyle\Sigma comme suit:
\begin{align}\Sigma = \frac{1}{m}\sum_{i = 1}^m(x^{(i)})(x^{(i)}) ^T. \end{align}
Si \textstyle x a une moyenne nulle, alors \textstyle\Sigma est exactement la matrice de covariance de \textstyle x. (Le symbole « \textstyle\Sigma », prononcé « Sigma », est la notation standard pour désigner la matrice de covariance. Malheureusement, cela ressemble au symbole de sommation, comme dans \sum_ {i = 1} ^n i; mais ce sont deux choses différentes.)
On peut alors montrer que \textstyle u_1 — la direction principale de variation des données – est le vecteur propre supérieur (principal) de \textstyle\Sigma, et \textstyle u_2 est le second vecteur propre.
Remarque: Si vous souhaitez voir une dérivation / justification mathématique plus formelle de ce résultat, consultez les notes de cours CS229 (Apprentissage automatique) sur PCA (lien en bas de cette page). Cependant, vous n’aurez pas besoin de le faire pour suivre ce cours.
Vous pouvez utiliser un logiciel d’algèbre linéaire numérique standard pour trouver ces vecteurs propres (voir les Notes d’implémentation). Concrètement, calculons les vecteurs propres de \textstyle\Sigma, et empilons les vecteurs propres en colonnes pour former la matrice \textstyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
Les vecteurs \textstyle u_1 et \textstyle u_2 dans notre exemple forment une nouvelle base dans laquelle nous pouvons représenter les données. Concrètement, soit \textstyle x\in\Re^2 un exemple d’entraînement. Alors \textstyle u_1 ^Tx est la longueur (magnitude) de la projection de \textstyle x sur le vecteur \textstyle u_1.
De même, \textstyle u_2^Tx est la grandeur de \textstyle x projetée sur le vecteur \textstyle u_2.
Rotation des Données
Ainsi, nous pouvons représenter \textstyle x dans la base \textstyle(u_1, u_2) en calculant
\begin{align}x_{\rm rot}=U^Tx=\begin{bmatrix}u_1^Tx\\u_2^Tx\end{bmatrix}\end{align}
(L’indice « rot » provient de l’observation que cela correspond à une rotation (et éventuellement une réflexion) de l’original données.) Prenons l’ensemble de la formation et calculons \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} pour chaque \textstyle i. En traçant ces données transformées \textstyle x_{\rm rot}, nous obtenons:

Il s’agit de l’ensemble d’entraînement pivoté dans la base \textstyle u_1, \textstyle u_2. Dans le cas général, \textstyle U^Tx sera l’ensemble d’entraînement pivoté dans la base \textstyle u_1, \textstyle u_2, …, \textstyle u_n.
Une des propriétés de \textstyle U est qu’il s’agit d’une matrice « orthogonale », ce qui signifie qu’elle satisfait \textstyle U^TU=UU^T =I. Donc, si jamais vous devez passer des vecteurs pivotés \textstyle x_{\rm rot} aux données d’origine \textstyle x, vous pouvez calculer
\begin{align} x= U x_{\rm rot}, \end{align}
parce que \textstyle U x_{\rm rot} = UU^T x = x.
En réduisant la dimension des données
Nous voyons que la direction principale de variation des données est la première dimension \textstyle x_{\rm rot} rm rot, 1} de ces données tournées. Ainsi, si nous voulons réduire ces données à une dimension, nous pouvons définir
\begin{align}\tilde{x}^{(i)} = x_{\rm rot, 1}^{(i)} = u_1^Tx^{(i)}\in\Re.\end{align}
Plus généralement, si \textstyle x\in\Re^n et que nous voulons le réduire à une représentation dimensionnelle \textstyle k\textstyle\tilde{x}\in\Re^k (où k <n), nous prendrions les premières composantes \textstyle k de \textstyle x_{\rm rot}, qui correspondent aux directions de variation supérieures \textstyle k.
Une autre façon d’expliquer PCA est que \textstyle x_{\rm rot} est un vecteur de dimension n \textstyle, où les premières composantes sont susceptibles d’être grandes (par ex., dans notre exemple, nous avons vu que \textstyle x_{\rm rot, 1}^{(i)} = u_1^Tx^{(i)} prend des valeurs raisonnablement grandes pour la plupart des exemples \textstyle i), et les composants ultérieurs sont susceptibles d’être petits (par exemple, dans notre exemple, \textstyle x_{\rm rot, 2}^{(i)} = u_2^Tx^{(i)} était plus susceptible d’être petit). Qu’est-ce que PCA fait, il supprime les composants les plus récents (plus petits) de \textstyle x_ {\rm rot}, et les rapproche simplement avec des 0. Concrètement, notre définition de \textstyle\tilde{x} peut également être obtenue en utilisant une approximation de \textstyle x_ {\rm rot} où tous les composants de \textstyle k sauf les premiers sont des zéros. En d’autres termes, nous avons:
\begin{align}\tilde{x} =\begin{bmatrix} x_{\rm rot, 1}\\\vdots\\x_{\rm rot, k}\\0\\\vdots\\0\\\end{bmatrix}\approx\begin{bmatrix} x_{\rm rot, 1}\\\vdots\\x_{\rm rot, k}\\x_{\rm rot, k +1}\ \\vdots \\x_{\rm rot, n}\end{bmatrix} = x_{\rm rot}\end{align}
Dans notre exemple, cela nous donne le tracé suivant de \textstyle\tilde{x} (en utilisant \textstyle n = 2, k = 1):

Cependant, comme les n-k composantes finales \textstyle de \textstyle\tilde{x} telles que définies ci-dessus seraient toujours nulles, il n’est pas nécessaire de garder ces zéros autour, et nous définissons donc \textstyle\tilde{x} comme un vecteur de dimension k \textstyle avec seulement les premières composantes \textstyle k (non nulles).
Cela explique également pourquoi nous voulions exprimer nos données dans la base \textstyle u_1, u_2, \ldots, u_n: Décider quels composants conserver devient simplement conserver les principaux composants \textstyle k. Lorsque nous faisons cela, nous disons également que nous « conservons les composants PCA (ou principaux) top\textstyle k. »
Récupération d’une approximation des données
Maintenant, \textstyle\tilde{x}\in\Re^k est une représentation « compressée » de dimension inférieure de l’original \textstyle x\in\Re^n. Étant donné \textstyle\tilde{x}, comment pouvons-nous récupérer une approximation \textstyle\hat{x} à la valeur d’origine de \textstyle x? D’une section précédente, nous savons que \textstyle x = U x_ {\rm rot}. De plus, nous pouvons penser à \textstyle\tilde{x} comme une approximation de \textstyle x_ {\rm rot}, où nous avons défini les derniers composants n-k de \textstyle sur des zéros. Ainsi, étant donné \textstyle\tilde{x}\in\Re^k, nous pouvons le tamponner avec \textstyle n-k zéros pour obtenir notre approximation à \textstyle x_{\rm rot}\in\Re^n. Enfin, nous pré-multiplions par \textstyle U pour obtenir notre approximation à \textstyle x. Concrètement, nous obtenons
\begin{align}\hat{x} =U\begin{bmatrix}\tilde{x} _1\\\vdots\\\tilde{ x}_k\\0\\\vdots\\0\ end {bmatrix} = \sum_ {i= 1} ^k u_i\tilde {x}_i. \end{align}
L’égalité finale ci-dessus provient de la définition de \textstyle U donnée précédemment. (Dans une implémentation pratique, nous ne metrions pas à zéro pad \textstyle\tilde {x}, puis nous multiplierions par \textstyle U, car cela signifierait multiplier beaucoup de choses par des zéros; au lieu de cela, nous multiplierions simplement \textstyle\tilde{x} \ in \Re ^k avec les premières colonnes \textstyle k de \textstyle U comme dans l’expression finale ci-dessus.) En appliquant cela à notre jeu de données, nous obtenons le tracé suivant pour \textstyle\hat{x}:
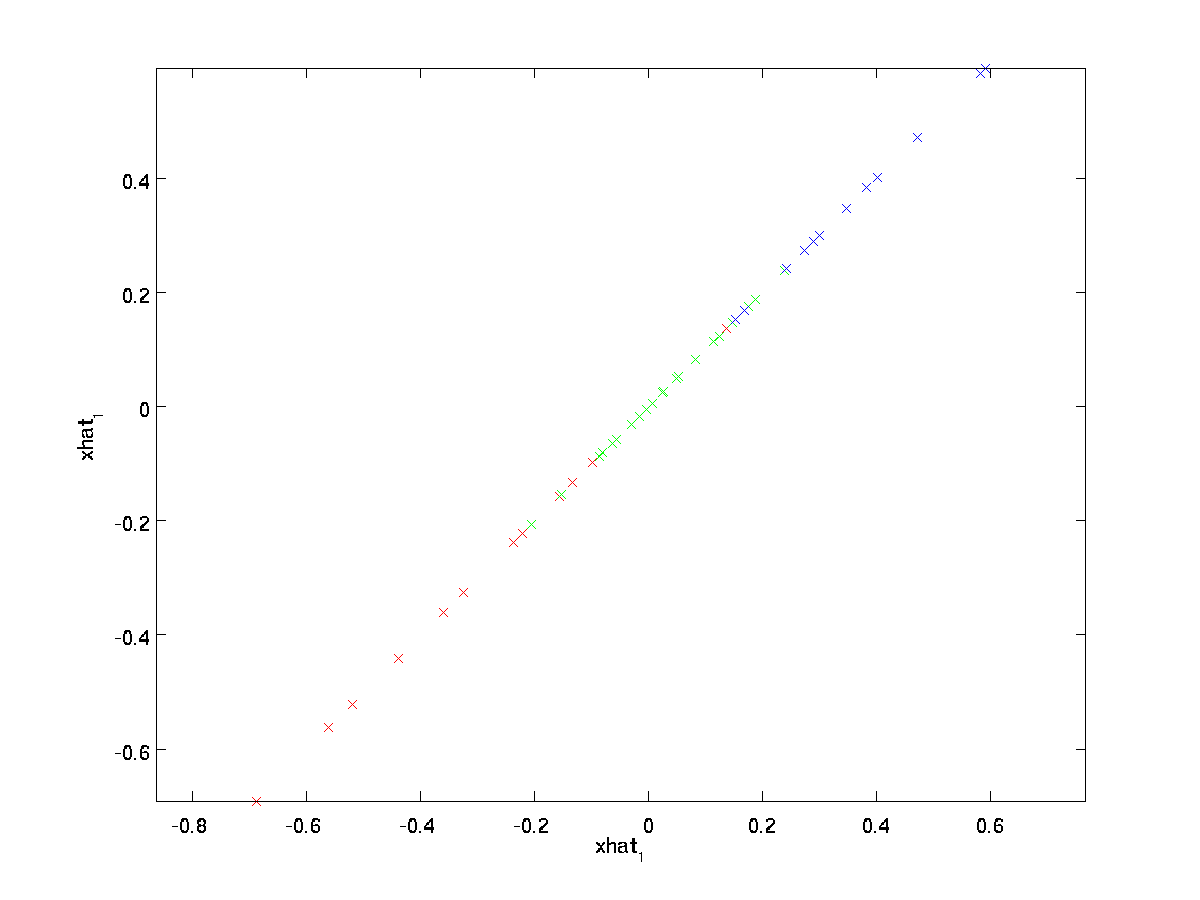
Nous utilisons donc une approximation à 1 dimension de l’ensemble de données d’origine.
Si vous entraînez un autoencodeur ou un autre algorithme d’apprentissage de fonctionnalités non supervisé, le temps d’exécution de votre algorithme dépendra de la dimension de l’entrée. Si vous introduisez \textstyle\tilde {x} \in \Re ^k dans votre algorithme d’apprentissage au lieu de \textstyle x, vous vous entraînerez sur une entrée de dimension inférieure et votre algorithme pourrait donc fonctionner beaucoup plus rapidement. Pour de nombreux ensembles de données, la représentation de dimension inférieure \textstyle \tilde {x} peut être une très bonne approximation de l’original, et l’utilisation de PCA de cette façon peut accélérer considérablement votre algorithme tout en introduisant très peu d’erreur d’approximation.
Nombre de composants à conserver
Comment définir \textstyle k; c’est-à-dire combien de composants PCA devons-nous conserver ? Dans notre exemple simple à 2 dimensions, il semblait naturel de retenir 1 des 2 composants, mais pour des données de dimensions supérieures, cette décision est moins triviale. Si \textstyle k est trop grand, nous ne compresserons pas beaucoup les données; dans la limite de \textstyle k = n, nous utilisons simplement les données d’origine (mais pivotées sur une base différente). Inversement, si \textstyle k est trop petit, nous pourrions utiliser une très mauvaise approximation des données.
Pour décider comment définir \textstyle k, nous examinerons généralement le « ‘pourcentage de variance retenu »‘ pour différentes valeurs de \textstyle k. Concrètement, si \textstyle k = n, nous avons une approximation exacte des données, et nous disons que 100% de la variance est conservée. C’est-à-dire, toute la variation des données d’origine est conservée. Inversement, si \textstyle k = 0, alors nous approchons toutes les données avec le vecteur zéro, et donc 0% de la variance est conservé.
Plus généralement, soit \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n les valeurs propres de \textstyle\Sigma (triées par ordre décroissant), de sorte que \textstyle\lambda_j est la valeur propre correspondant au vecteur propre \textstyle u_j. Ensuite, si nous conservons \textstyle k composantes principales, le pourcentage de variance retenu est donné par:
\begin {align}\frac {\sum_{j=1}^k\lambda_j} {\sum_{j=1}^n\lambda_j}.\end{align}
Dans notre exemple 2D simple ci-dessus, \textstyle\lambda_1=7.29 et \textstyle\lambda_2=0.69. Ainsi, en ne gardant que \textstyle k = 1 composants principaux, nous avons conservé \textstyle 7.29/(7.29+0.69) = 0.913, soit 91,3 % de la variance.
Une définition plus formelle du pourcentage de variance retenu dépasse la portée de ces notes. Cependant, il est possible de montrer que \textstyle\lambda_j = \sum_{i = 1}^m x_ {\rm rot, j}^2. Ainsi, si \textstyle\lambda_j\approx 0, cela montre que \textstyle x_{\rm rot, j} est généralement proche de 0 de toute façon, et nous perdons relativement peu en l’approchant avec une constante 0. Cela explique également pourquoi nous conservons les composants principaux du haut (correspondant aux valeurs plus grandes de \textstyle\lambda_j) au lieu des composants du bas. Les composantes principales supérieures \textstyle x_ {\rm rot,j} sont celles qui sont les plus variables et qui prennent des valeurs plus grandes, et pour lesquelles nous aurions une erreur d’approximation plus importante si nous les mettions à zéro.
Dans le cas des images, une heuristique courante consiste à choisir \textstyle k de manière à conserver 99% de la variance. En d’autres termes, nous choisissons la plus petite valeur de \textstyle k qui satisfait
\begin{align}\frac{\sum_{j=1}^k\lambda_j}{\sum_{j=1}^n\lambda_j}\geq 0.99. \end{align}
Selon l’application, si vous êtes prêt à subir une erreur supplémentaire, des valeurs comprises entre 90 et 98% sont parfois utilisées. Lorsque vous décrivez à d’autres comment vous avez appliqué PCA, dire que vous avez choisi \textstyle k pour conserver 95% de la variance sera également une description beaucoup plus facilement interprétable que de dire que vous avez conservé 120 (ou tout autre nombre de) composants.
PCA sur les images
Pour que PCA fonctionne, nous voulons généralement que chacune des entités \textstyle x_1, x_2, \ldots, x_n ait une plage de valeurs similaire aux autres (et une moyenne proche de zéro). Si vous avez déjà utilisé PCA sur d’autres applications, il se peut donc que vous ayez prétraité séparément chaque fonctionnalité pour avoir une moyenne et une variance unitaires nulles, en estimant séparément la moyenne et la variance de chaque fonctionnalité \textstyle x_j. Cependant, ce n’est pas le prétraitement que nous appliquerons à la plupart des types d’images. Plus précisément, supposons que nous entraînions notre algorithme sur des « »images naturelles » », de sorte que \textstyle x_j est la valeur de pixel \textstyle j. Par « images naturelles », nous entendons de manière informelle le type d’image qu’un animal ou une personne typique pourrait voir au cours de sa vie.
Remarque: Habituellement, nous utilisons des images de scènes extérieures avec de l’herbe, des arbres, etc., et découpez de petits correctifs d’image (disons 16×16) de manière aléatoire à partir de ceux-ci pour entraîner l’algorithme. Mais dans la pratique, la plupart des algorithmes d’apprentissage des fonctionnalités sont extrêmement robustes au type exact d’image sur laquelle ils sont entraînés, de sorte que la plupart des images prises avec un appareil photo normal, tant qu’elles ne sont pas trop floues ou ne contiennent pas d’artefacts étranges, devraient fonctionner.
Lors de l’entraînement sur des images naturelles, il n’a guère de sens d’estimer une moyenne et une variance distinctes pour chaque pixel, car les statistiques d’une partie de l’image devraient (théoriquement) être les mêmes que les autres.
Cette propriété des images est appelée « ‘stationnarité. »‘
En détail, pour que la PCA fonctionne bien, de manière informelle, nous exigeons que (i) Les caractéristiques aient une moyenne approximativement nulle et (ii) Les différentes caractéristiques ont des variances similaires les unes aux autres. Avec des images naturelles, (ii) est déjà satisfait même sans normalisation de la variance, et nous n’effectuerons donc aucune normalisation de la variance.
(Si vous vous entraînez sur des données audio – disons, sur des spectrogrammes – ou sur des données textuelles — disons, des vecteurs en sac de mots – nous n’effectuerons généralement pas non plus de normalisation de la variance.)
En fait, PCA est invariant à la mise à l’échelle des données et renverra les mêmes vecteurs propres quelle que soit la mise à l’échelle de l’entrée. Plus formellement, si vous multipliez chaque vecteur d’entités \textstyle x par un nombre positif (mettant ainsi à l’échelle chaque entité de chaque exemple d’entraînement par le même nombre), les vecteurs propres de sortie de PCA ne changeront pas.
Donc, nous n’utiliserons pas la normalisation de la variance. La seule normalisation que nous devons effectuer est alors la normalisation moyenne, pour nous assurer que les entités ont une moyenne autour de zéro. Selon l’application, très souvent, nous ne sommes pas intéressés par la luminosité de l’image d’entrée globale. Par exemple, dans les tâches de reconnaissance d’objets, la luminosité globale de l’image n’affecte pas les objets présents dans l’image. Plus formellement, nous ne nous intéressons pas à la valeur d’intensité moyenne d’un patch d’image; ainsi, nous pouvons soustraire cette valeur, comme une forme de normalisation moyenne.
Concrètement, si \textstyle x^{(i)}\in\Re^{n} sont les valeurs d’intensité (en niveaux de gris) d’un patch d’image 16×16 (\textstyle n = 256), nous pourrions normaliser l’intensité de chaque image \textstyle x^{(i)} comme suit:
\mu^{(i)}: = \frac{1}{n}\sum_{j = 1}^n x^{(i)}_jx^{(i ) }_j :=x^{(i)}_j-\mu^{(i)}
pour tout \textstyle j
Notez que les deux étapes ci-dessus sont effectuées séparément pour chaque image \textstyle x^{(i)}, et que \textstyle\mu^{(i)} voici l’intensité moyenne de l’image \textstyle x^{(i)}. En particulier, ce n’est pas la même chose que d’estimer une valeur moyenne séparément pour chaque pixel\textstyle x_j.
Si vous entraînez votre algorithme sur des images autres que des images naturelles (par exemple, des images de caractères manuscrits ou des images d’objets isolés centrés sur un fond blanc), d’autres types de normalisation peuvent être envisagés, et le meilleur choix peut dépendre de l’application. Mais lors de l’entraînement sur des images naturelles, l’utilisation de la méthode de normalisation de la moyenne par image donnée dans les équations ci-dessus serait un défaut raisonnable.
Blanchiment
Nous avons utilisé le PCA pour réduire la dimension des données. Il existe une étape de prétraitement étroitement liée appelée blanchiment (ou, dans certaines autres littératures, sphering) qui est nécessaire pour certains algorithmes. Si nous nous entraînons sur des images, l’entrée brute est redondante, car les valeurs de pixels adjacents sont fortement corrélées. Le but du blanchiment est de rendre l’entrée moins redondante; plus formellement, nos désidérata sont que nos algorithmes d’apprentissage voient une entrée d’entraînement où (i) les caractéristiques sont moins corrélées les unes aux autres, et (ii) les caractéristiques ont toutes la même variance.
Exemple 2D
Nous allons d’abord décrire le blanchiment en utilisant notre exemple 2D précédent. Nous décrirons ensuite comment cela peut être combiné avec le lissage, et enfin comment combiner cela avec le PCA.
Comment rendre nos fonctionnalités d’entrée non corrélées les unes avec les autres ? Nous l’avions déjà fait lors du calcul de \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}.
En répétant notre figure précédente, notre tracé pour \textstyle x_{\rm rot} était:

La matrice de covariance de ces données est donnée par:
\begin{align}\begin{bmatrix}7.29 && 0,69\end {bmatrix}.\end {align}
(Remarque: Techniquement, de nombreuses déclarations de cette section sur la « covariance » ne seront vraies que si les données ont une moyenne nulle. Dans le reste de cette section, nous prendrons cette hypothèse comme implicite dans nos déclarations. Cependant, même si la moyenne des données n’est pas exactement nulle, les intuitions que nous présentons ici sont toujours vraies, et ce n’est donc pas quelque chose dont vous devriez vous inquiéter.)
Ce n’est pas un hasard si les valeurs diagonales sont \textstyle\lambda_1 et \textstyle\lambda_2. De plus, les entrées hors diagonale sont nulles; ainsi, \textstyle x_{\rm rot, 1} et \textstyle x_{\rm rot, 2} ne sont pas corrélés, satisfaisant l’un de nos desiderata pour les données blanchies (que les caractéristiques soient moins corrélées).
Pour que chacune de nos entités d’entrée ait une variance unitaire, nous pouvons simplement redimensionner chaque entité \textstyle x_{\rm rot, i} par \textstyle 1/\sqrt{\lambda_i}. Concrètement, nous définissons nos données blanchies \textstyle x_{\rm PCAwhite}\in\Re^n comme suit:
\begin{align}x_{\rm PCAwhite, i}=\frac{x_{\rm rot, i}}{\sqrt{\lambda_i}}. \end{align}
Traçage \textstyle x_ {\rm PCAwhite}, nous obtenons:

Ces données ont maintenant une covariance égale à la matrice d’identité \textstyle I. Nous disons que \textstyle x_{\rm PCAwhite} est notre version blanchie PCA des données: Les différentes composantes de \textstyle x_{\rm PCAwhite} ne sont pas corrélées et ont une variance unitaire.
Blanchiment associé à une réduction de la dimensionnalité. Si vous souhaitez avoir des données blanchies et de dimension inférieure à l’entrée d’origine, vous pouvez également ne conserver que les composants supérieurs \textstyle k de \textstyle x_ {\rm PCAwhite}. Lorsque nous combinons le blanchiment PCA avec la régularisation (décrite plus loin), les derniers composants de \textstyle x_ {\rm PCAwhite} seront de toute façon presque nuls et pourront donc être supprimés en toute sécurité.
Blanchiment ZCA
Enfin, il s’avère que cette façon d’obtenir que les données aient une identité de covariance \textstyle I n’est pas unique. Concrètement, si \textstyle R est une matrice orthogonale quelconque, de sorte qu’elle satisfasse \textstyle RR^T = R^TR =I (de manière moins formelle, si \textstyle R est une matrice de rotation/réflexion), alors \textstyle R\, x_{\rm PCAwhite} aura également une covariance d’identité.
Dans le blanchiment ZCA, nous choisissons \textstyle R=U. Nous définissons
\begin{align}x_{\rm ZCAwhite}=U x_{\rm PCAwhite}\end{align}
Traçage \textstyle x_{\rm ZCAwhite}, nous obtenons :

On peut montrer que sur tous les choix possibles pour \textstyle R, ce choix de rotation fait que \textstyle x_ {\rm ZCAwhite} est aussi proche que possible des données d’entrée d’origine \textstyle x.
Lors de l’utilisation du blanchiment ZCA (contrairement au blanchiment PCA), nous conservons généralement toutes les dimensions \textstyle n des données et n’essayons pas de réduire sa dimension.
Regularizaton
Lors de la mise en œuvre du blanchiment PCA ou du blanchiment ZCA dans la pratique, certaines des valeurs propres \textstyle\lambda_i seront numériquement proches de 0, et donc l’étape de mise à l’échelle où nous divisons par \sqrt{\lambda_i} impliquerait de diviser par une valeur proche de zéro; cela peut faire exploser les données (prendre de grandes valeurs) ou autrement être numériquement instable. En pratique, nous implémentons donc cette étape de mise à l’échelle en utilisant une petite quantité de régularisation, et ajoutons une petite constante \textstyle\epsilon aux valeurs propres avant de prendre leur racine carrée et inverse:
\begin{align} x_{\rm PCAwhite, i} =\frac{x_{\rm rot, i}}{\sqrt{\lambda_i+\epsilon}}.\end{align}
Lorsque \textstyle x prend des valeurs autour de \textstyle, une valeur de \textstyle\epsilon\environ 10^{-5} peut être typique.
Pour le cas des images, l’ajout de \textstyle\epsilon ici a également pour effet de lisser légèrement (ou de filtrer passe-bas) l’image d’entrée. Cela a également pour effet souhaitable de supprimer les artefacts de repliement causés par la façon dont les pixels sont disposés dans une image, et peut améliorer les caractéristiques apprises (les détails dépassent la portée de ces notes).
Le blanchiment ZCA est une forme de prétraitement des données qui les mappe de \textstyle x à \textstyle x_{\rm ZCAwhite}. Il s’avère qu’il s’agit également d’un modèle approximatif de la façon dont l’œil biologique (la rétine) traite les images. Plus précisément, lorsque votre œil perçoit des images, la plupart des « pixels » adjacents de votre œil percevront des valeurs très similaires, car les parties adjacentes d’une image ont tendance à être fortement corrélées en intensité. Il est donc inutile pour votre œil de devoir transmettre chaque pixel séparément (via votre nerf optique) à votre cerveau. Au lieu de cela, votre rétine effectue une opération de décorrélation (cela se fait via des neurones rétiniens qui calculent une fonction appelée « on center, off surround / off center, on surround ») qui est similaire à celle effectuée par ZCA. Il en résulte une représentation moins redondante de l’image d’entrée, qui est ensuite transmise à votre cerveau.
Mise en œuvre du blanchiment PCA
Dans cette section, nous résumons les algorithmes de blanchiment PCA, de blanchiment PCA et de blanchiment ZCA, et décrivons également comment vous pouvez les implémenter à l’aide de bibliothèques d’algèbre linéaire efficaces.
Tout d’abord, nous devons nous assurer que les données ont une moyenne (approximativement) nulle. Pour les images naturelles, nous y parvenons (approximativement) en soustrayant la valeur moyenne de chaque patch d’image.
Nous y parvenons en calculant la moyenne de chaque patch et en la soustrayant pour chaque patch. Dans Matlab, nous pouvons le faire en utilisant
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);Ensuite, nous devons calculer \textstyle\Sigma = \frac{1}{m}\sum_{i =1}^m(x^{(i)})(x^{(i)}) ^T. Si vous implémentez cela dans Matlab (ou même si vous implémentez cela en C++, Java , etc., mais avoir accès à une bibliothèque d’algèbre linéaire efficace), le faire comme une somme explicite est inefficace. Au lieu de cela, nous pouvons calculer cela d’un seul coup comme
sigma = x * x' / size(x, 2);(Vérifiez vous-même l’exactitude des calculs.) Ici, nous supposons que x est une structure de données qui contient un exemple d’entraînement par colonne (donc, x est une matrice \textstyle n-by-\textstyle m).
Ensuite, PCA calcule les vecteurs propres de \Sigma. On pourrait le faire en utilisant la fonction eig Matlab. Cependant, comme \Sigma est une matrice semi-définie positive symétrique, il est plus fiable numériquement de le faire en utilisant la fonction svd. Concrètement, si vous implémentez
= svd(sigma);alors la matrice U contiendra les vecteurs propres de \Sigma (un vecteur propre par colonne, trié dans l’ordre du vecteur propre de haut en bas), et les entrées diagonales de la matrice S contiendront les valeurs propres correspondantes (également triées par ordre décroissant). La matrice V sera égale à U, et peut être ignorée en toute sécurité.
(Remarque: La fonction svd calcule en fait les vecteurs singuliers et les valeurs singulières d’une matrice, qui pour le cas particulier d’une matrice semi-définie positive symétrique — qui est tout ce qui nous concerne ici — est égale à ses vecteurs propres et valeurs propres. Une discussion complète des vecteurs singuliers par rapport aux vecteurs propres dépasse la portée de ces notes.)
Enfin, vous pouvez calculer \textstyle x_{\rm rot} et \textstyle\tilde{x} comme suit:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepCela donne à votre représentation PCA des données en termes de \textstyle\tilde{x}\in\Re^k. Incidemment, si x est une matrice \textstyle n-by-\textstyle m contenant toutes vos données d’entraînement, il s’agit d’une implémentation vectorisée, et les expressions ci-dessus fonctionnent également pour calculer x_{\rm rot} et \tilde{x} pour l’ensemble de votre ensemble d’entraînement en une seule fois. Les x_{\rm rot} et \tilde{x} résultants auront une colonne correspondant à chaque exemple d’entraînement.
Pour calculer les données blanchies PCA \textstyle x_{\rm PCAwhite}, utilisez
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;Puisque la diagonale de S contient les valeurs propres \textstyle\lambda_i, cela s’avère être un moyen compact de calculer \textstyle x_{\rm PCAwhite, i} =\frac{x_{\rm rot, i}} {\sqrt {\lambda_i}} simultanément pour tous les \textstyle i.
Enfin, vous pouvez également calculer les données blanchies ZCA \textstyle x_{\rm ZCAwhite} comme:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;