
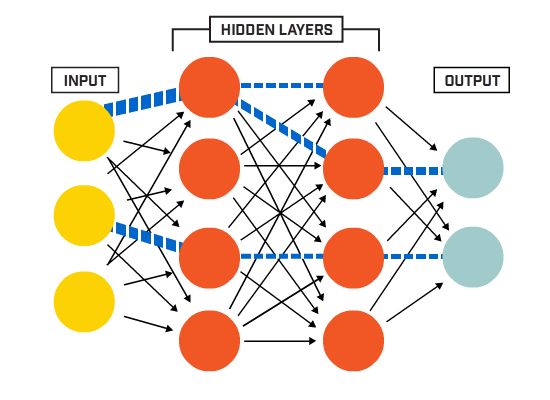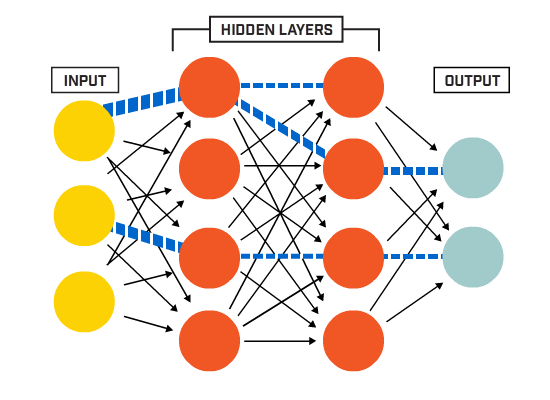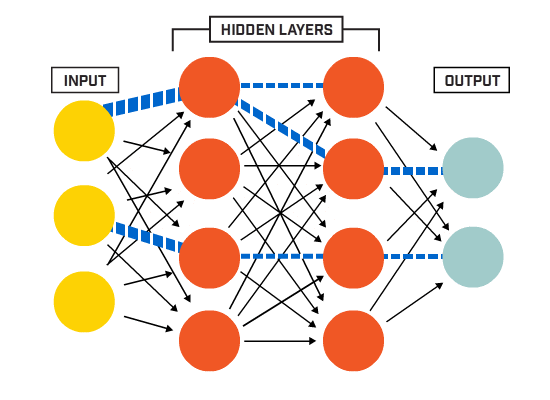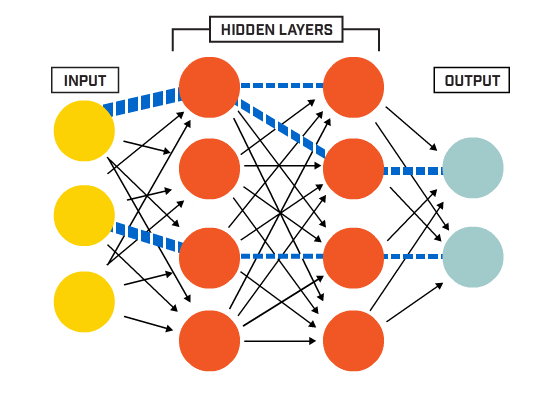
Una Red Neuronal Artificial (ANN) está formada por muchas neuronas interconectadas:
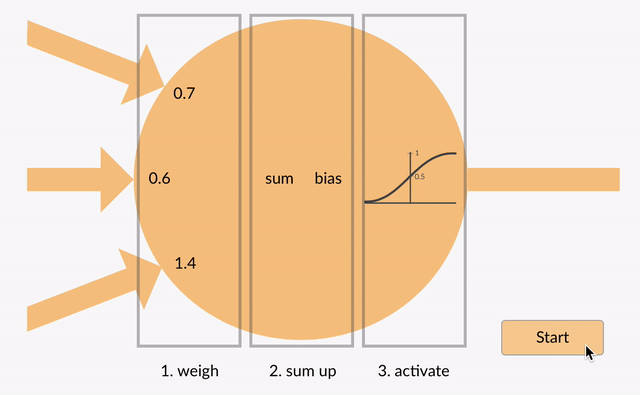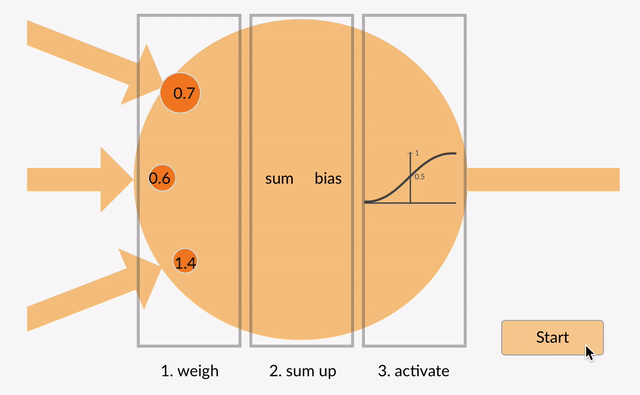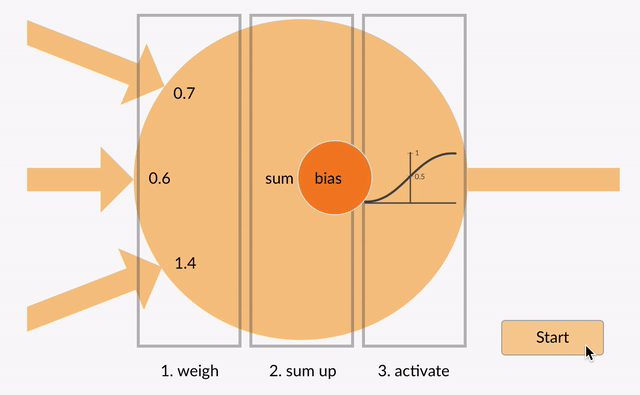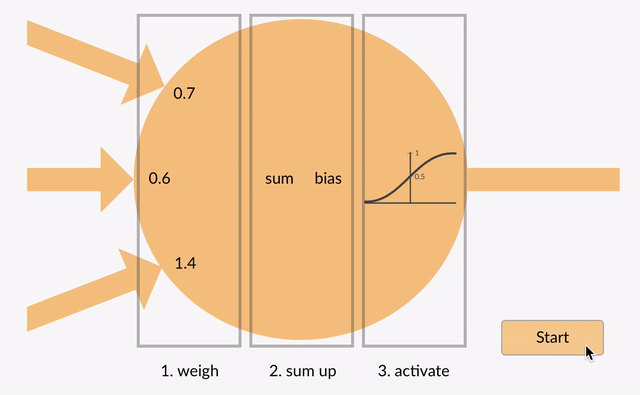
Cada neurona toma algunos números de coma flotante (por ejemplo, 1.0, 0.5, -1).0) y los multiplica por otros números de coma flotante (por ejemplo, 0.7, 0.6, 1.4) conocidos como pesos (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Las ponderaciones actúan como un mecanismo para centrarse en, o ignorar, ciertas entradas.

El promedio ponderado de los insumos, a continuación, obtener suman (por ejemplo, 0.7 + 0.3 + -1.4 = -0.4) junto con un valor de sesgo (por ejemplo, -0.4 + -0.1 = -0.5).
El valor sumado (x) se transforma ahora en un valor de salida (y) de acuerdo con la función de activación de la neurona (y = f(x)). A continuación se muestran algunas funciones de activación populares:

por ejemplo, -0.5 → -0.05 si utilizamos la función de activación de la Unidad Lineal rectificada con fugas (ReLU con fugas): y = f(x) = f(-0.5) = max(0.1*-0.5, -0.5) = max(-0.05, -0.5) = -0.05
El valor de salida de la neurona (por ejemplo, -0.05) es a menudo una entrada para otra neurona.
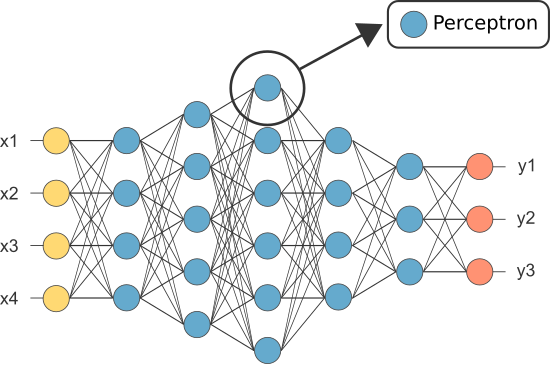
sin Embargo, uno de los primeros Rna fue conocido como el tipo perceptrón y consistía de una sola neurona.

La salida de la (única) neurona del perceptrón actúa como predicción final.

Permite codificar nuestro propio Perceptrón:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Nota: no hemos incluido cualquier algoritmo de aprendizaje en nuestro ejemplo anterior, vamos a cubrir los algoritmos de aprendizaje en otro tutorial)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

Entonces, ¿por qué necesitamos tantas neuronas en una ANN si alguna es suficiente (como clasificador)?

Desafortunadamente, las neuronas individuales solo pueden clasificar datos separables linealmente.

sin Embargo, mediante la combinación de las neuronas juntos, podemos combinar esencialmente su decisión límites. Por lo tanto, una RNA compuesta de muchas neuronas es capaz de aprender límites de decisión complejos y no lineales.

Las neuronas están conectadas entre sí de acuerdo con una arquitectura de red específica. Aunque hay diferentes arquitecturas, casi todas contienen capas. (NOTA:: Las neuronas de la misma capa no se conectan entre sí)
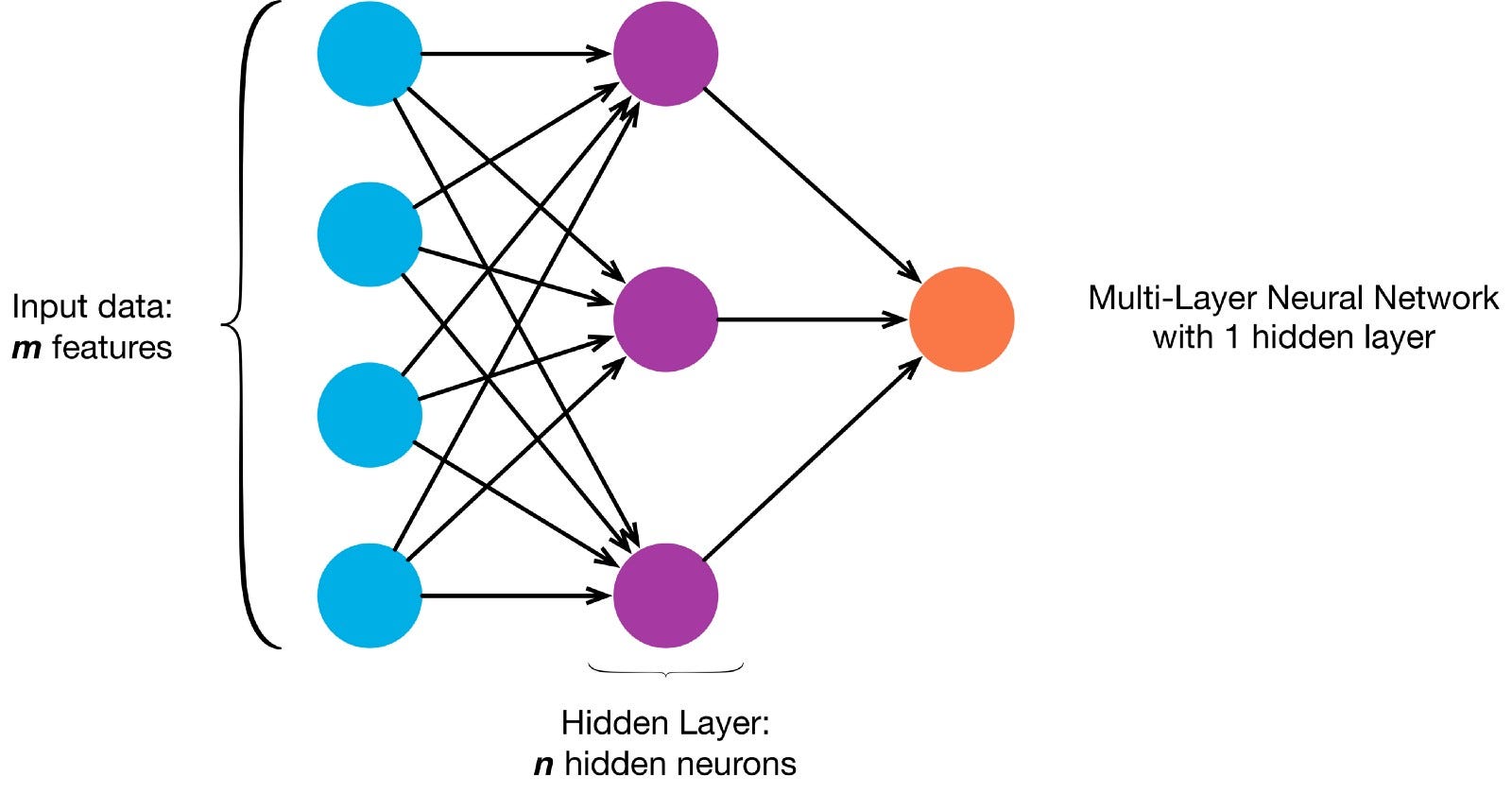
Normalmente hay una capa de entrada (que contiene varias neuronas igual al número de entidades de entrada en los datos), una capa de salida (que contiene un número de neuronas igual al número de clases) y una capa oculta (que contiene cualquier número de neuronas).

Puede haber más de una capa oculta para permitir que la red neuronal aprenda límites de decisión más complejos (Cualquier red con más de una capa oculta se considera una red neuronal profunda).
Construyamos un NN profundo para pintar esta imagen:

la imagen y cargar sus píxeles en una matriz
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
Ahora enseñar a pintar a nuestra ANN es una tarea de aprendizaje supervisada, por lo que necesitamos crear un conjunto de entrenamiento etiquetado (Nuestros datos de entrenamiento tendrán entradas y etiquetas de salida esperadas para cada entrada). Las entradas de entrenamiento tendrán 2 valores (las coordenadas x,y de cada píxel).
Dada la simplicidad de la imagen, podríamos abordar este problema de una de dos maneras. Un problema de clasificación (donde la red neuronal predice si un píxel pertenece a la clase» azul «o a la clase» gris», dadas sus coordenadas xy) o un problema de regresión (donde la red neuronal predice valores RGB para un píxel dadas sus coordenadas).
Si se trata de un problema de regresión: las salidas de entrenamiento tendrán 3 valores (los valores normalizados r,g,b para cada píxel). – Usemos este método por ahora.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Ahora vamos a crear nuestra ANN:

- Debe tener 2 neuronas en la capa de entrada (ya que hay 2 valores a tomar: x & coordenadas y).
- Debe tener 3 neuronas en la capa de salida (ya que hay 3 valores para aprender: r, g, b).
- El número de capas ocultas y el número de neuronas en cada capa oculta son dos hiperparámetros con los que experimentar (así como el número de épocas para las que lo entrenaremos, la función de activación, etc.): Usaré 10 capas ocultas con 100 neuronas en cada capa oculta (haciendo de esta una red neuronal profunda)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
La red entrenada ahora puede predecir los valores rgb normalizados para por ejemplo,x, y = 1,1).
ann.predict(])
array(])
vamos a usar la AN para predecir los valores rgb para cada coordenada y vamos a mostrar los valores rgb previstos para toda la imagen para ver qué tan bien lo hizo (cualitativamente, dejaremos las métricas de evaluación para otro tutorial)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

Intente cambiar los hiperparámetros para obtener mejores resultados.
Si en lugar de tratar esto como un problema de regresión, lo tratamos como un problema de clasificación, entonces las salidas de entrenamiento tendrán 2 valores (las probabilidades del píxel perteneciente a cada una de las dos clases: «azul» y «gris»)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
Podemos reconstruir nuestra ANN como un clasificador binario con 2 neuronas en la capa de entrada, 2 neuronas en la capa de salida y 100 neuronas en la capa oculta (con 10 capas ocultas)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
Ahora podemos usar la ANN entrenada para predecir la clase a la que pertenece cada píxel (0: «gris» o 1: «azul»). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: «grey»)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

