Las redes residuales profundas (ResNet) conquistaron el mundo del aprendizaje profundo cuando Microsoft Research lanzó el Aprendizaje Residual profundo para el Reconocimiento de imágenes. Estas redes condujeron a las entradas ganadoras del 1er lugar en las cinco pistas principales de los concursos ImageNet y COCO 2015, que cubrieron la clasificación de imágenes, la detección de objetos y la segmentación semántica. Desde entonces, la robustez de los ResNet ha sido demostrada por varias tareas de reconocimiento visual y por tareas no visuales que involucran el habla y el lenguaje. También utilicé ResNet, además de otros modelos de aprendizaje profundo en mi investigación de tesis doctoral.
Este post resumirá los tres documentos a continuación, todos escritos o coescritos por el inventor de ResNet Kaiming He, porque creo que los documentos originales dan la explicación más intuitiva y detallada del modelo / redes. Con suerte, esta publicación podría ayudarte a comprender mejor la esencia de las redes residuales.
- Aprendizaje Residual Profundo para Reconocimiento de imágenes
- Asignaciones de identidad en Redes Residuales Profundas
- Transformación Residual Agregada para Redes Neuronales Profundas
- Intuición en Redes Residuales Profundas (stackoverflow ref)
- Aprendizaje Residual Profundo para el Reconocimiento de imágenes
- Problema
- Ver Degradarse en acción:
- ¿Cómo resolver?
- Intuición detrás de bloques residuales:
- Casos de prueba:
- Diseñar la red:
- Resultados
- Estudios más profundos
- Observaciones
- Asignaciones de identidad en Redes Residuales Profundas
- Introducción
- Análisis de redes residuales profundas
- Importancia de las conexiones de salto de identidad
- Experimentos con Conexiones de salto
- Uso de funciones de activación
- Experimentos de activación
- Conclusión
- Transformación Residual Agregada para Redes Neuronales Profundas
- Introducción
- Método
- Experimentos
Intuición en Redes Residuales Profundas (stackoverflow ref)
Un bloque residual se muestra de la siguiente manera:
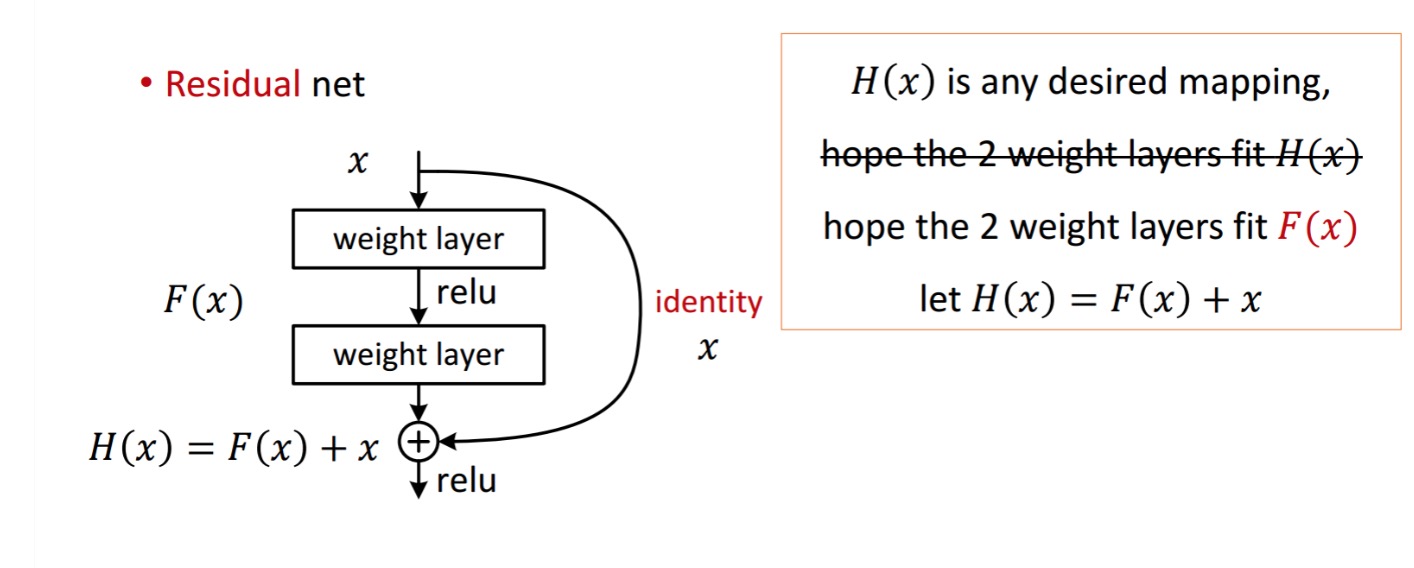
Por lo tanto, la unidad residual que se muestra se obtiene procesando con dos capas de peso. Luego se suma a obtener . Ahora, supongamos que es su salida predecida ideal que coincide con su verdad de tierra. Dado que , obtener lo deseado depende de obtener lo perfecto . Eso significa que las dos capas de peso en la unidad residual deben ser capaces de producir lo deseado, y entonces se garantiza la obtención del ideal.
se obtiene de la siguiente manera.
se obtiene de la siguiente manera.
Los autores plantean la hipótesis de que el mapeo residual (es decir,) puede ser más fácil de optimizar que . Para ilustrar con un ejemplo simple, supongamos que el ideal . Entonces, para un mapeo directo, sería difícil aprender un mapeo de identidad, ya que hay una pila de capas no lineales de la siguiente manera.
Por lo tanto, aproximar el mapeo de identidad con todos estos pesos y ReLUs en el medio sería difícil.
Ahora, si definimos la asignación deseada, solo necesitamos obtener de la siguiente manera.
Lograr lo anterior es fácil. Simplemente establezca cualquier peso en cero y obtendrá una salida cero. Agregue de nuevo y obtendrá el mapeo deseado.
Aprendizaje Residual Profundo para el Reconocimiento de imágenes
Problema
Cuando las redes más profundas comienzan a converger, se ha expuesto un problema de degradación: con el aumento de la profundidad de la red, la precisión se satura y luego se degrada rápidamente.
Ver Degradarse en acción:
Tomemos una red superficial y su contraparte más profunda agregándole más capas.
En el peor de los casos: Las primeras capas del modelo más profundo se pueden reemplazar por una red poco profunda y las capas restantes solo pueden actuar como una función de identidad (Entrada igual a salida).
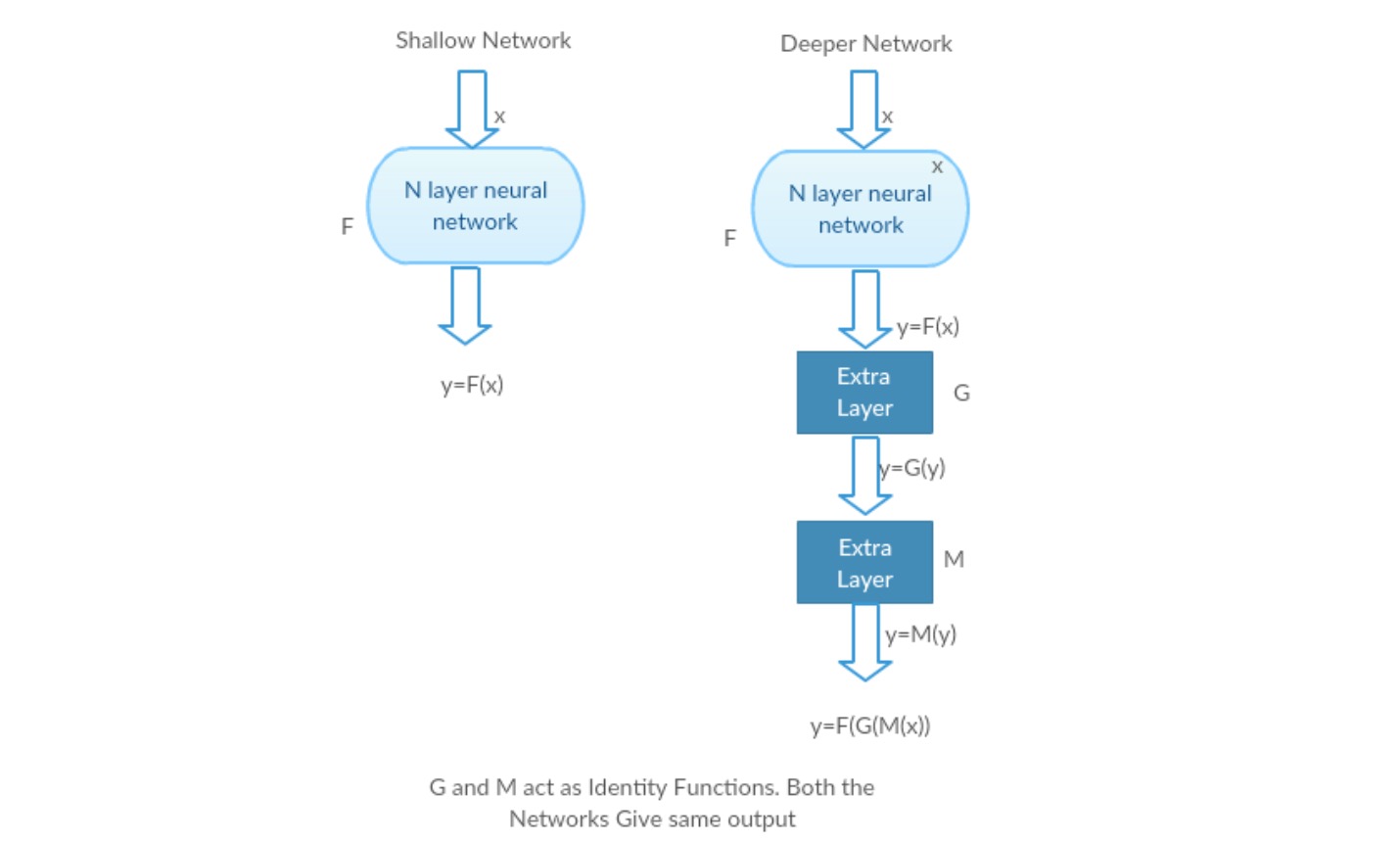
Escenario gratificante: En la red más profunda, las capas adicionales se aproximan mejor a la asignación que a la parte del contador menos profunda y reducen el error en un margen significativo.
Experimento: En el peor de los casos, tanto la red superficial como la variante más profunda de la misma deberían dar la misma precisión. En el caso del escenario gratificante, el modelo más profundo debe dar una mayor precisión que la parte del contador menos profunda. Pero los experimentos con nuestros solucionadores actuales revelan que los modelos más profundos no funcionan bien. Por lo tanto, el uso de redes más profundas está degradando el rendimiento del modelo. Estos documentos intentan resolver este problema utilizando un marco de aprendizaje Residual profundo.
¿Cómo resolver?
En lugar de aprender un mapeo directo de con una función (unas pocas capas apiladas no lineales). Definamos la función residual usando, que se puede reformular, donde y representa las capas no lineales apiladas y la función de identidad(entrada=salida) respectivamente.
La hipótesis del autor es que es fácil optimizar la función de asignación residual que optimizar la asignación original sin referencias .
Intuición detrás de bloques residuales:
Tomemos el mapeo de identidad como ejemplo (p. ej. ). Si la asignación de identidad es óptima, podemos empujar fácilmente los residuos a cero () en lugar de ajustar una asignación de identidad () por una pila de capas no lineales. En un lenguaje simple, es muy fácil encontrar una solución como, en lugar de usar una pila de capas de cnn no lineales como función (piénsalo). Por lo tanto, esta función es lo que los autores llamaron Función residual.
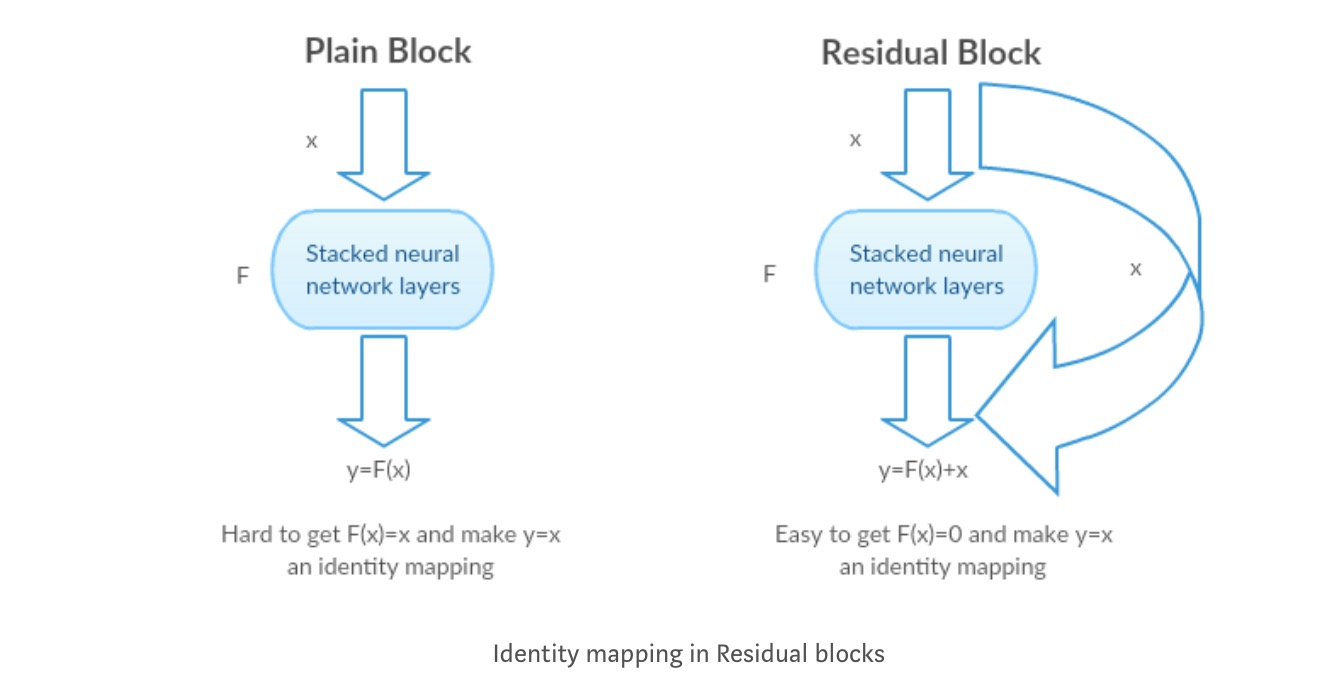
Los autores realizaron varias pruebas para probar su hipótesis. Echemos un vistazo a cada uno de ellos ahora.
Casos de prueba:
Tome una red simple (red de 18 capas de tipo VGG) (Red-1) y una variante más profunda de la misma (34 capas, Red-2) y agregue capas residuales a la Red-2 (34 capas con conexiones residuales, Red-3).
Diseñar la red:
- Utilice filtros 3 * 3 en su mayoría.
- Muestreo descendente con capas de CNN con stride 2.
- Capa de agrupación media global y una capa de 1000 vías totalmente conectada con Softmax al final.

Hay dos tipos de conexiones residuales:
I. Los accesos directos de identidad () se pueden usar directamente cuando la entrada () y la salida () tienen las mismas dimensiones.
II. Cuando las dimensiones cambian, A) El acceso directo sigue realizando asignaciones de identidad, con entradas adicionales de cero rellenadas con la dimensión aumentada. B) El acceso directo de proyección se utiliza para coincidir con la dimensión (hecho por conv 1 * 1) utilizando la siguiente fórmula
Resultados
Aunque la red de 18 capas es solo el subespacio en la red de 34 capas, aún funciona mejor. ResNet supera por un margen significativo en caso de que la red sea más profunda
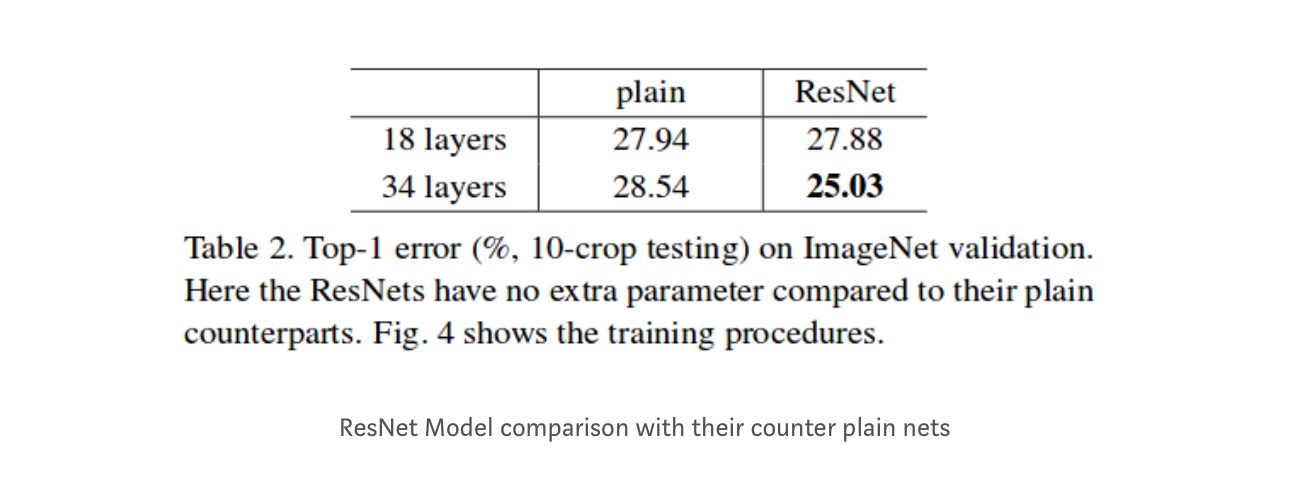
Estudios más profundos
Además, se estudian más redes:

Cada bloque de ResNet tiene una profundidad de 2 capas (utilizado en redes pequeñas como ResNet 18, 34) o 3 capas de profundidad( ResNet 50, 101, 152).
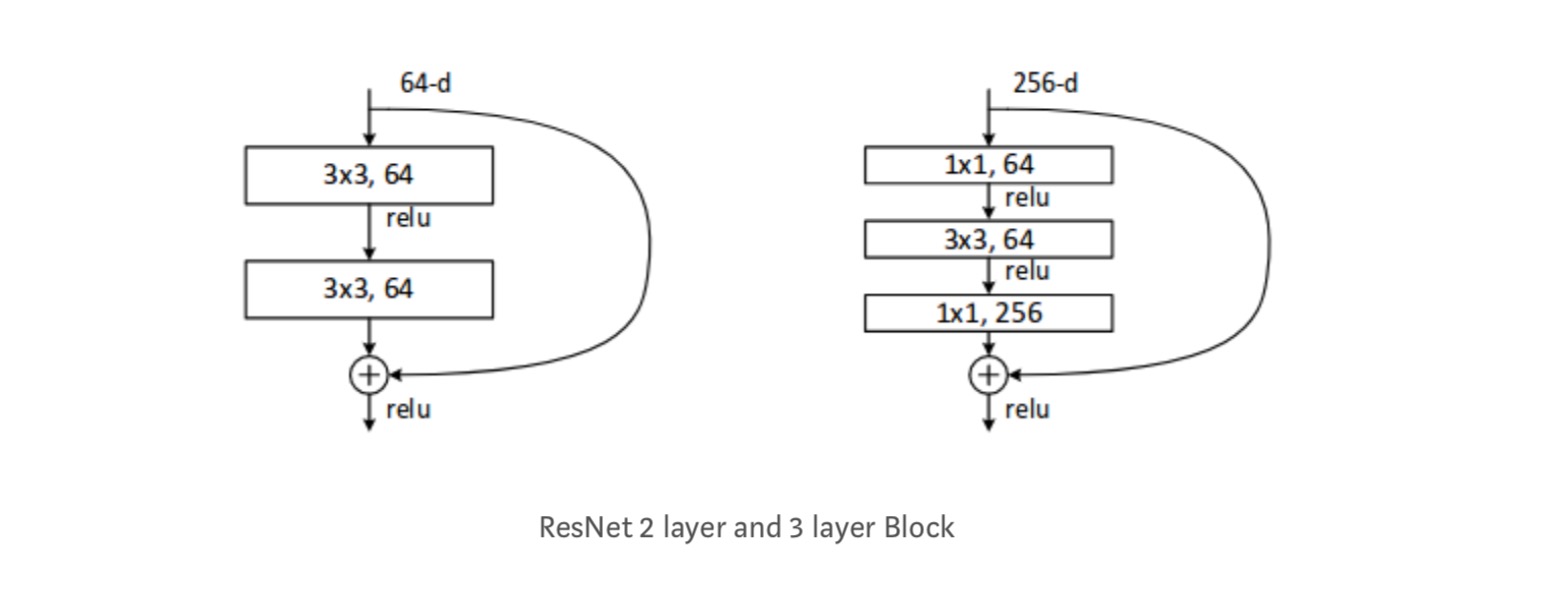
Observaciones
- La red ResNet Converge más rápido en comparación con la parte de contador simple de la misma.
- Identidad vs shorcuts de proyección. Ganancias incrementales muy pequeñas utilizando atajos de proyección (Ecuación-2) en todas las capas. Por lo tanto, todos los bloques de ResNet solo usan accesos directos de identidad con accesos directos de proyecciones que se usan solo cuando cambian las dimensiones.
- ResNet-34 logró un error de validación top-5 de 5,71% mejor que BN-inception y VGG. ResNet-152 logra un error de validación top-5 del 4,49%. Un conjunto de 6 modelos con diferentes profundidades logra un error de validación de top-5 del 3,57%. Ganando el 1er lugar en ILSVRC-2015
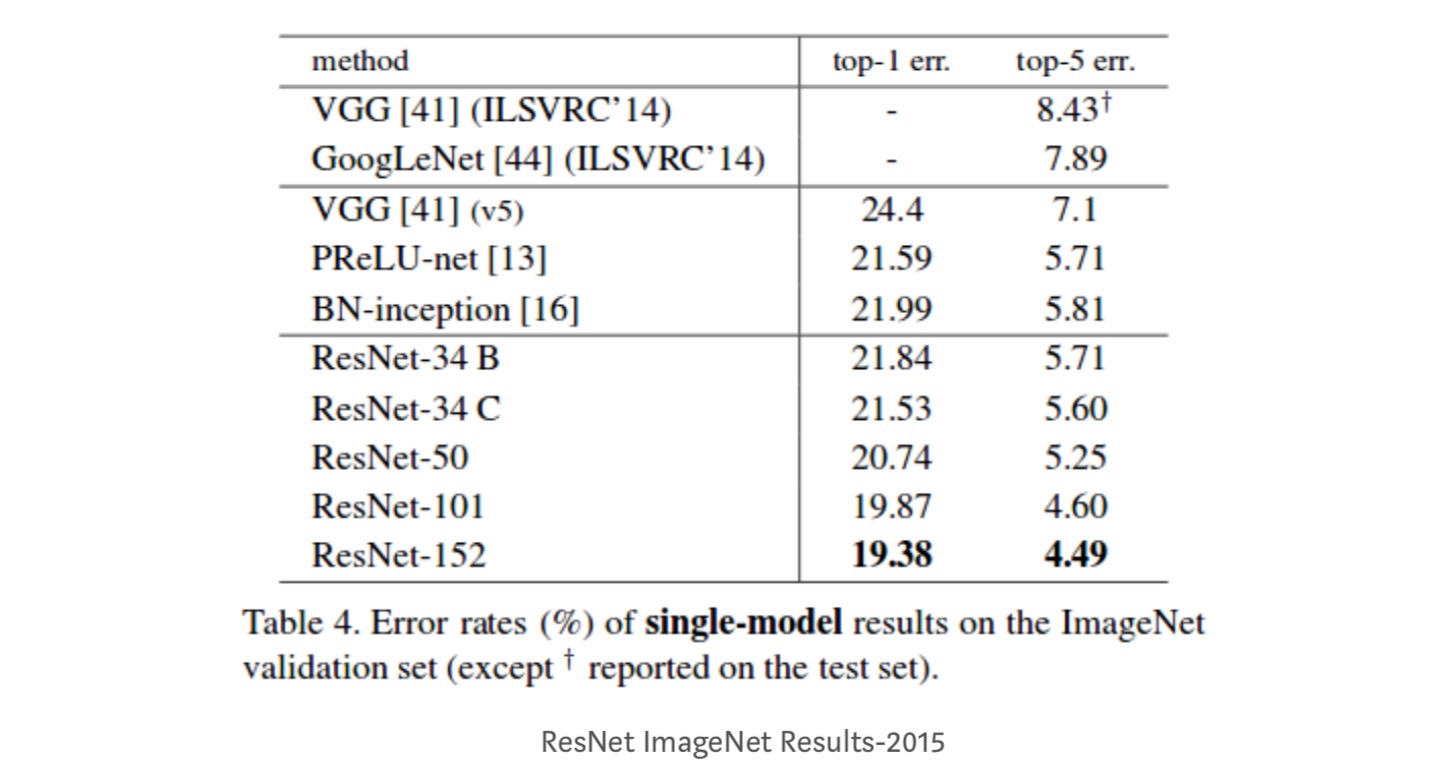
Asignaciones de identidad en Redes Residuales Profundas
Este documento proporciona la comprensión teórica de por qué el problema de gradiente de fuga no está presente en redes residuales y el papel de las conexiones de salto (las conexiones de salto significan la entrada o ) reemplazando la asignación de identidad (x) con diferentes funciones.
Introducción
Las redes residuales profundas consisten en muchas «Unidades residuales» apiladas. Cada unidad se puede expresar de una forma general:
donde y son entrada y salida de la unidad, y es una función residual. En el último documento, es un mapeo de identidad y es una función ReLU.
La idea central de los ResNet es aprender la función residual aditiva con respecto a, con una opción clave de usar un mapeo de identidad . Esto se realiza adjuntando una conexión de omisión de identidad («atajo»).
En este artículo, analizamos redes residuales profundas centrándose en crear una ruta «directa» para propagar información, no solo dentro de una unidad residual, sino a través de toda la red. Nuestras derivaciones revelan que si ambos y son asignaciones de identidad, la señal podría propagarse directamente de una unidad a cualquier otra, tanto en pasadas hacia adelante como hacia atrás. Nuestros experimentos demuestran empíricamente que el entrenamiento en general se hace más fácil cuando la arquitectura está más cerca de las dos condiciones anteriores.
Para comprender el papel de las conexiones de salto, analizamos y comparamos varios tipos de . Encontramos que el mapeo de identidad elegido en el último documento logra la reducción de errores más rápida y la pérdida de entrenamiento más baja entre todas las variantes que investigamos, mientras que las conexiones de salto de escalado, compuerta y circunvoluciones de 1×1 conducen a mayores pérdidas y errores de entrenamiento. Estos experimentos sugieren que mantener una ruta de información» limpia » es útil para facilitar la optimización.
Para construir un mapeo de identidad, vemos las funciones de activación (ReLU y BN) como «preactivación» de las capas de peso, en contraste con la sabiduría convencional de «postactivación». Este punto de vista conduce a un nuevo diseño de unidad residual, que se muestra en la siguiente figura. Con base en esta unidad, presentamos resultados competitivos en CIFAR-10/100 con una red de 1001 capas, que es mucho más fácil de entrenar y generaliza mejor que la red original. Además, informamos de resultados mejorados en ImageNet utilizando una red de 200 capas, para la que la contraparte del último documento comienza a sobreajustarse. Estos resultados sugieren que hay mucho espacio para explotar la dimensión de la profundidad de red, una clave para el éxito del aprendizaje profundo moderno.
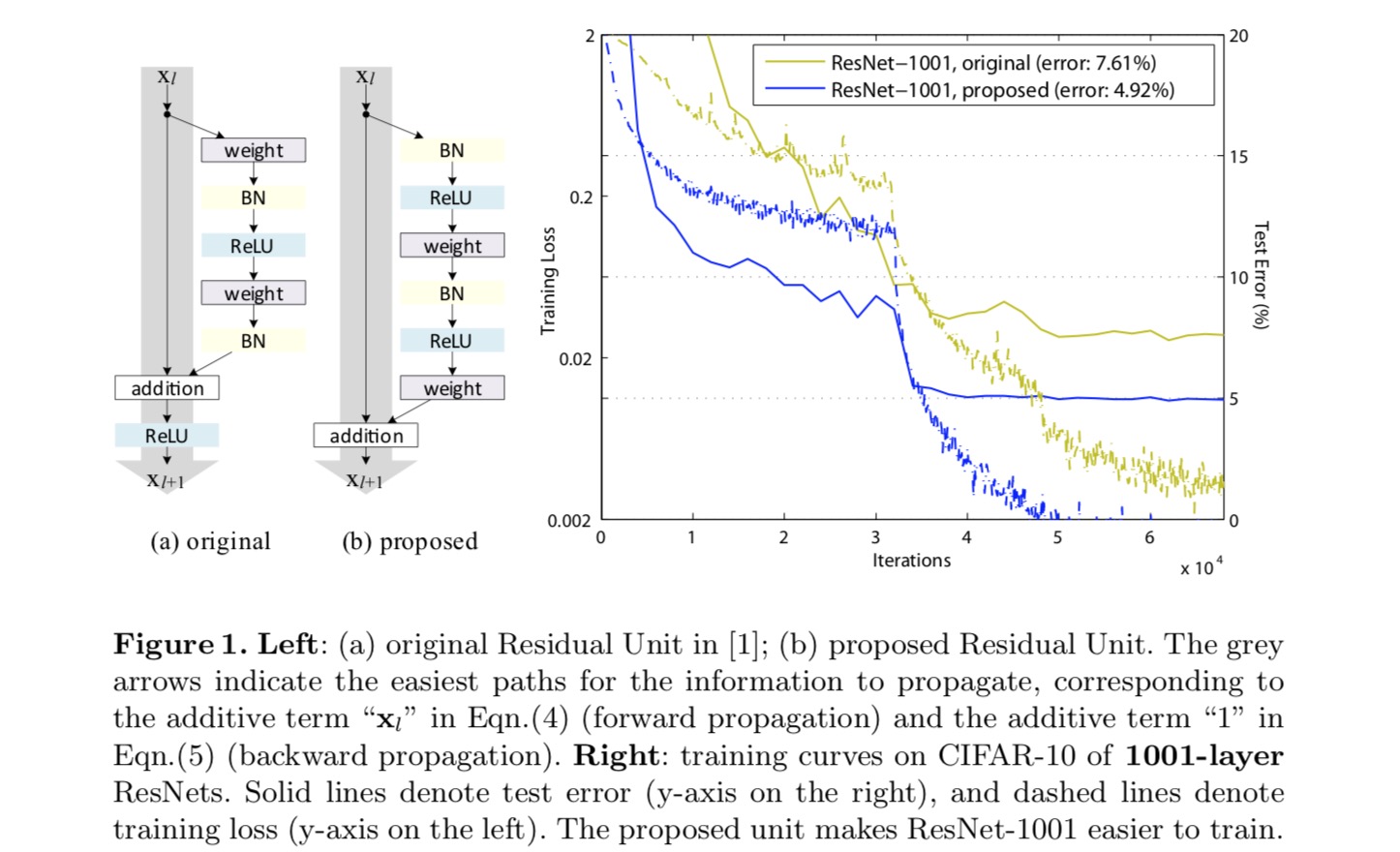
Análisis de redes residuales profundas
Los ResNets desarrollados en el último documento son arquitecturas modulares que apilan bloques de construcción de la misma forma de conexión. En este artículo llamamos a estos bloques «Unidades Residuales». La Unidad Residual original en el último documento realiza el siguiente cálculo:
Aquí está la función de entrada a la Unidad Residual-ésima. es un conjunto de pesos (y sesgos) asociados con la Unidad Residual-ésima, y es el número de capas en una Unidad Residual ( es 2 o 3 en el último documento). indica la función residual, e.g., una pila de dos capas convolucionales de 3×3 en el último papel. La función es la operación después de la adición de elementos, y en el último documento es ReLU. La función se establece como asignación de identidad:.
Si también es un mapeo de identidad:, podemos obtener:
Recursivamente tendremos:
para cualquier unidad más profunda y cualquier unidad menos profunda . Esta ecuación exhibe algunas propiedades agradables. (1) La característica de cualquier unidad más profunda se puede representar como la característica de cualquier unidad menos profunda más una función residual en una forma de , lo que indica que el modelo está en una forma residual entre cualquier unidad y . (2) La característica, de cualquier unidad profunda, es la suma de las salidas de todas las funciones residuales precedentes (más ). Esto contrasta con una «red simple» donde una característica es una serie de productos matriz-vector, por ejemplo, (ignorando BN y ReLU).
La ecuación anterior también conduce a buenas propiedades de propagación hacia atrás. Denotando la función de pérdida como, de la regla de cadena de backpropagation tenemos:
La ecuación anterior indica que el gradiente se puede descomponer en dos términos aditivos: un término de que propaga información directamente sin referirse a ninguna capa de peso, y otro término de que se propaga a través de las capas de peso. El término aditivo de asegura que la información se propaga directamente a cualquier unidad menos profunda l. La ecuación anterior también sugiere que es poco probable que el gradiente se cancele para un mini-lote, porque en general el término no siempre puede ser -1 para todas las muestras en un mini-lote. Esto implica que el gradiente de una capa no desaparece incluso cuando los pesos son arbitrariamente pequeños.
Las dos ecuaciones anteriores sugieren que la señal puede propagarse directamente de cualquier unidad a otra, tanto hacia adelante como hacia atrás. La base de las dos primeras ecuaciones anteriores son dos asignaciones de identidad: (1) la conexión de exclusión de identidad y (2) la condición que es una asignación de identidad.
Importancia de las conexiones de salto de identidad
Consideremos una simple modificación,, para romper el atajo de identidad:
donde está un escalar modulante (para simplificar, todavía asumimos que es identidad). Aplicando recursivamente esta formulación obtenemos una ecuación similar a la anterior:
donde la notación absorbe los escalares en las funciones residuales. De manera similar, tenemos la contrapropagación de la siguiente forma:
A diferencia de la ecuación anterior, en esta ecuación el primer término aditivo es modulado por un factor . Para una red extremadamente profunda (es grande), si para todos , este factor puede ser exponencialmente grande; si para todos , este factor puede ser exponencialmente pequeño y desaparecer, lo que bloquea la señal contrapropagada del atajo y la fuerza a fluir a través de las capas de peso. Esto resulta en dificultades de optimización, como se muestra en los experimentos.
En el análisis anterior, la conexión de salto de identidad original se reemplaza con una escala simple . Si la conexión de salto representa transformaciones más complicadas (como compuertas y convoluciones de 1×1), en la ecuación anterior el primer término se convierte en donde es la derivada de . Este producto también puede impedir la propagación de la información y dificultar el procedimiento de entrenamiento, como se observa en los siguientes experimentos.
Experimentos con Conexiones de salto
Experimentamos con la red de 110 capas en CIFAR-10. Este ResNet-110 extremadamente profundo tiene 54 Unidades Residuales de dos capas (que consisten en capas convolucionales de 3×3) y es un desafío para la optimización. Se experimentan varios tipos de conexiones de salto. Vea la siguiente figura:
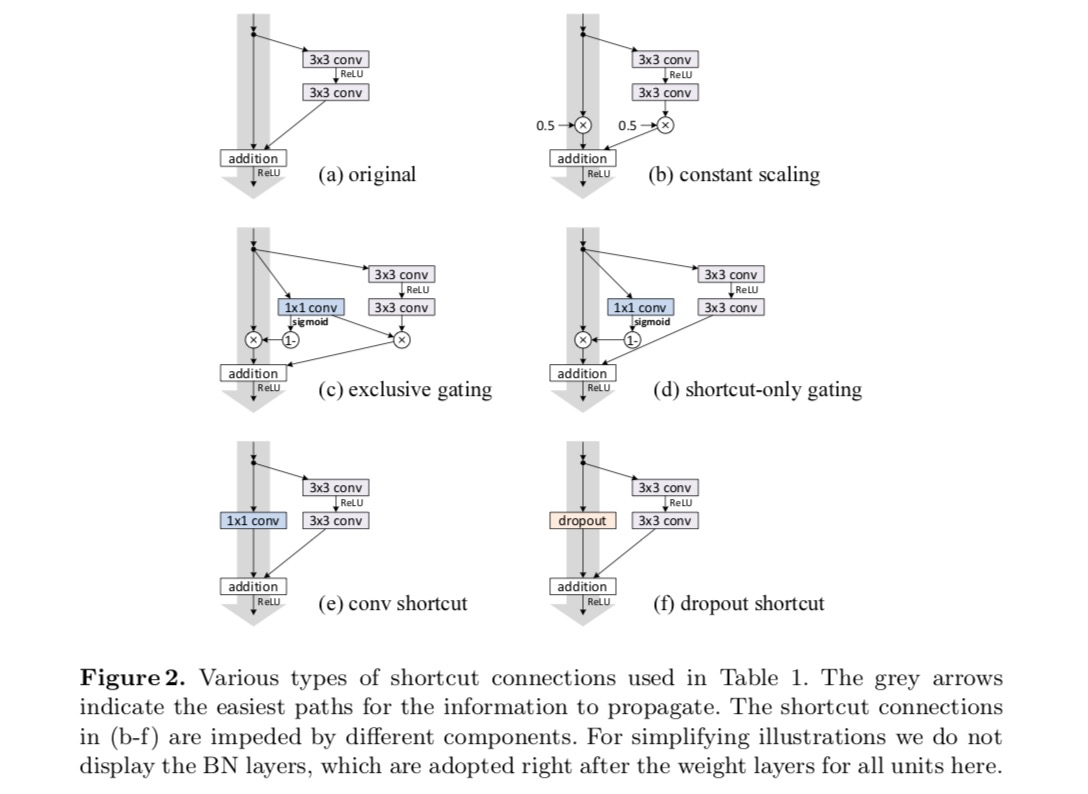
Los resultados de la clasificación se muestran en la siguiente tabla:
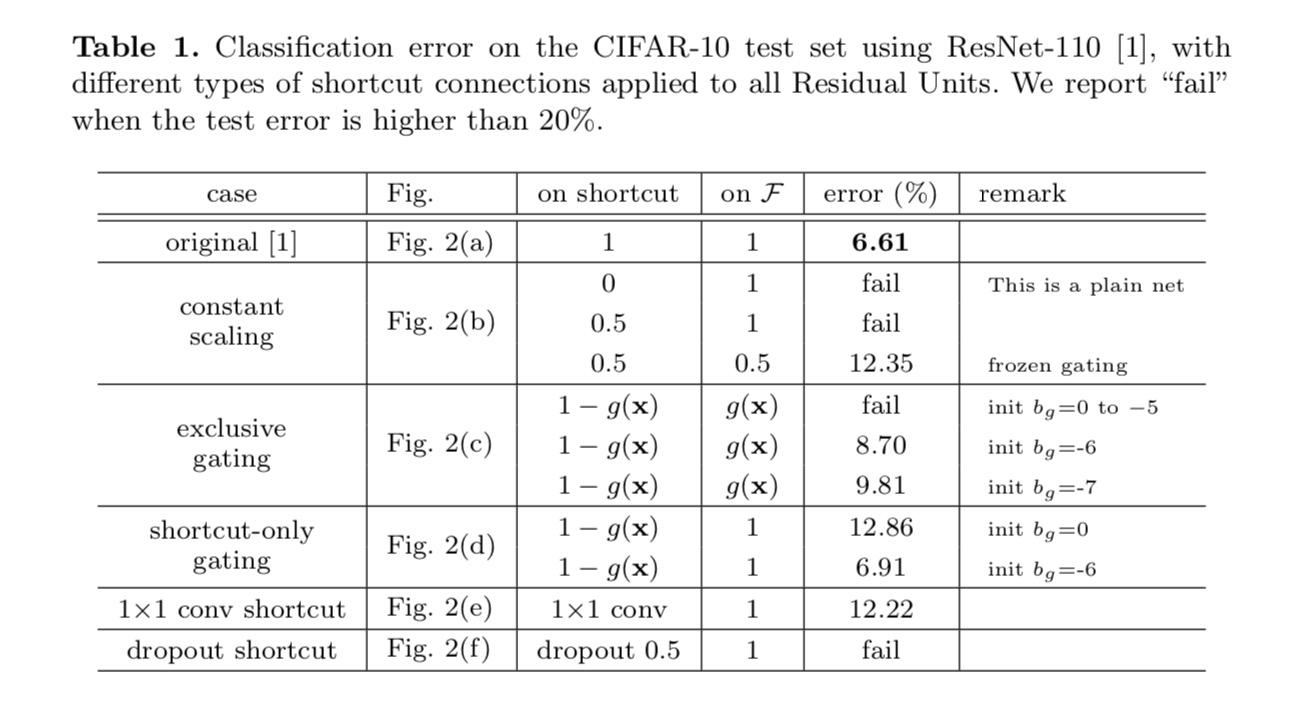
Como se indica en las flechas grises de la figura anterior, las conexiones de acceso directo son las rutas más directas para que la información se propague. Las manipulaciones multiplicativas (escalado, compuerta, circunvoluciones de 1×1 y abandono) en los accesos directos pueden obstaculizar la propagación de la información y provocar problemas de optimización.
Es de destacar que los atajos convolucionales de gating y 1×1 introducen más parámetros, y deben tener habilidades de representación más fuertes que los atajos de identidad. De hecho, la compuerta de acceso directo y la convolución de 1×1 cubren el espacio de solución de los accesos directos de identidad (es decir, podrían optimizarse como accesos directos de identidad). Sin embargo, su error de entrenamiento es mayor que el de los atajos de identidad, lo que indica que la degradación de estos modelos es causada por problemas de optimización, en lugar de habilidades de representación.
Uso de funciones de activación
Los experimentos de la sección anterior se basan en el supuesto de que la activación posterior a la adición es la asignación de identidad. Pero en los experimentos anteriores se ReLU como se diseñó en el primer documento. A continuación investigamos el impacto de .
Queremos hacer un mapeo de identidad, que se realiza reorganizando las funciones de activación (ReLU y/o BN, normalización por lotes). En la figura siguiente, la Unidad Residual original del último papel tiene una forma en la Fig. 4 (a) – BN se utiliza después de cada capa de peso, y ReLU se adopta después de BN, excepto que el último ReLU en una Unidad Residual es después de la adición de elementos ( = ReLU). Higo. 4 (b-e) mostrar las alternativas que investigamos.
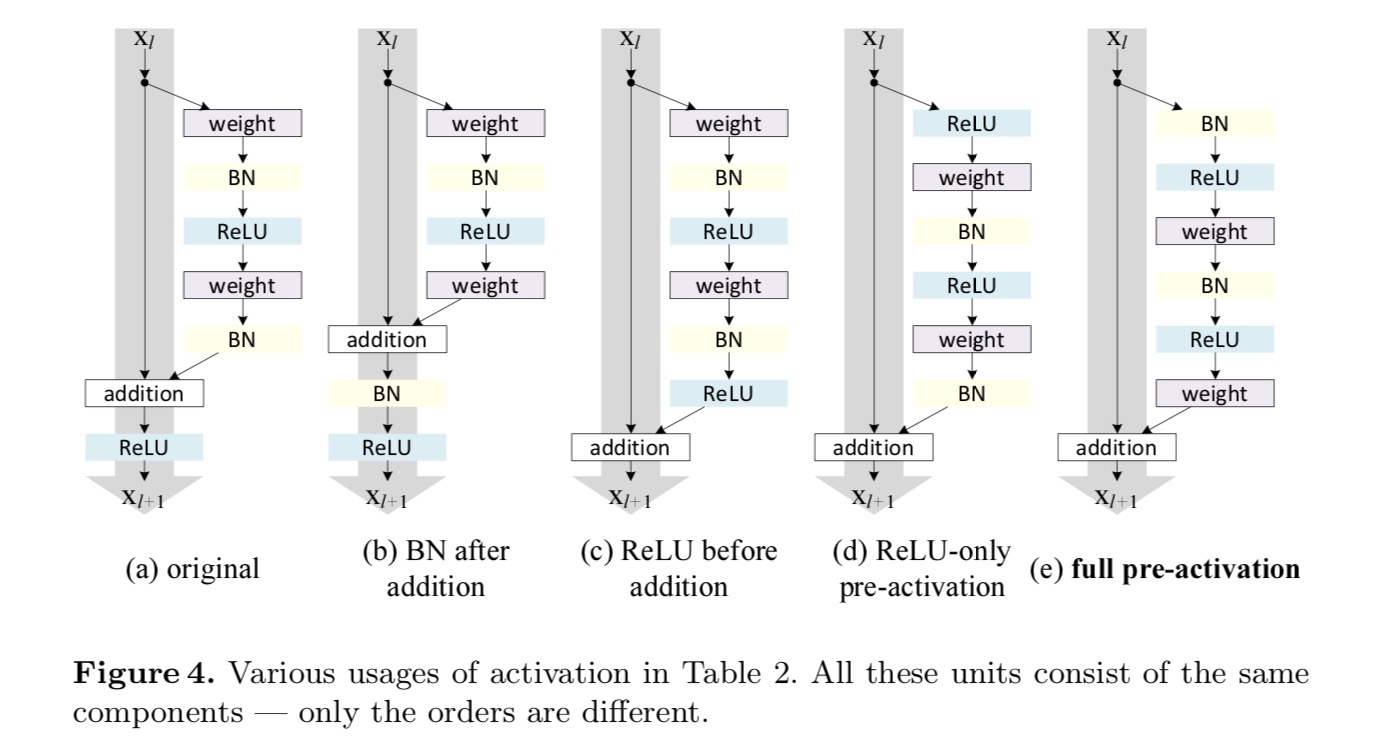
Experimentos de activación
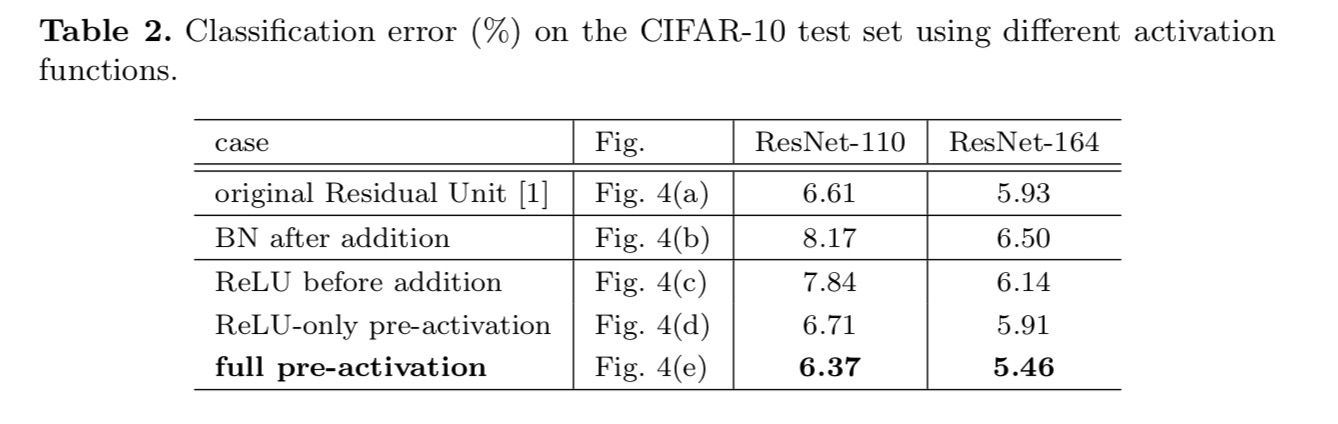
En esta sección experimentamos con ResNet-110 y una arquitectura de cuello de botella de 164 capas (denotada como ResNet-164). Una Unidad residual de cuello de botella consiste en una capa de 1×1 para reducir la dimensión, una capa de 3×3 y una capa de 1×1 para restaurar la dimensión. Tal como se diseñó en el último documento, su complejidad computacional es similar a la Unidad Residual de dos-3×3.
¿Post-activación o pre-activación?
En el diseño original, la activación afecta a ambas rutas en la siguiente Unidad residual: . A continuación desarrollamos una forma asimétrica donde una activación solo afecta al camino:, para cualquiera . Al cambiar el nombre de las notaciones, tenemos la siguiente forma:
Para esta nueva Unidad Residual como en la ecuación anterior, la nueva activación posterior a la adición se convierte en una asignación de identidad. Este diseño significa que si se adopta asimétricamente una nueva activación posterior a la adición, es equivalente a la refundición como la preactivación de la siguiente Unidad Residual. Esto se ilustra en la siguiente figura:
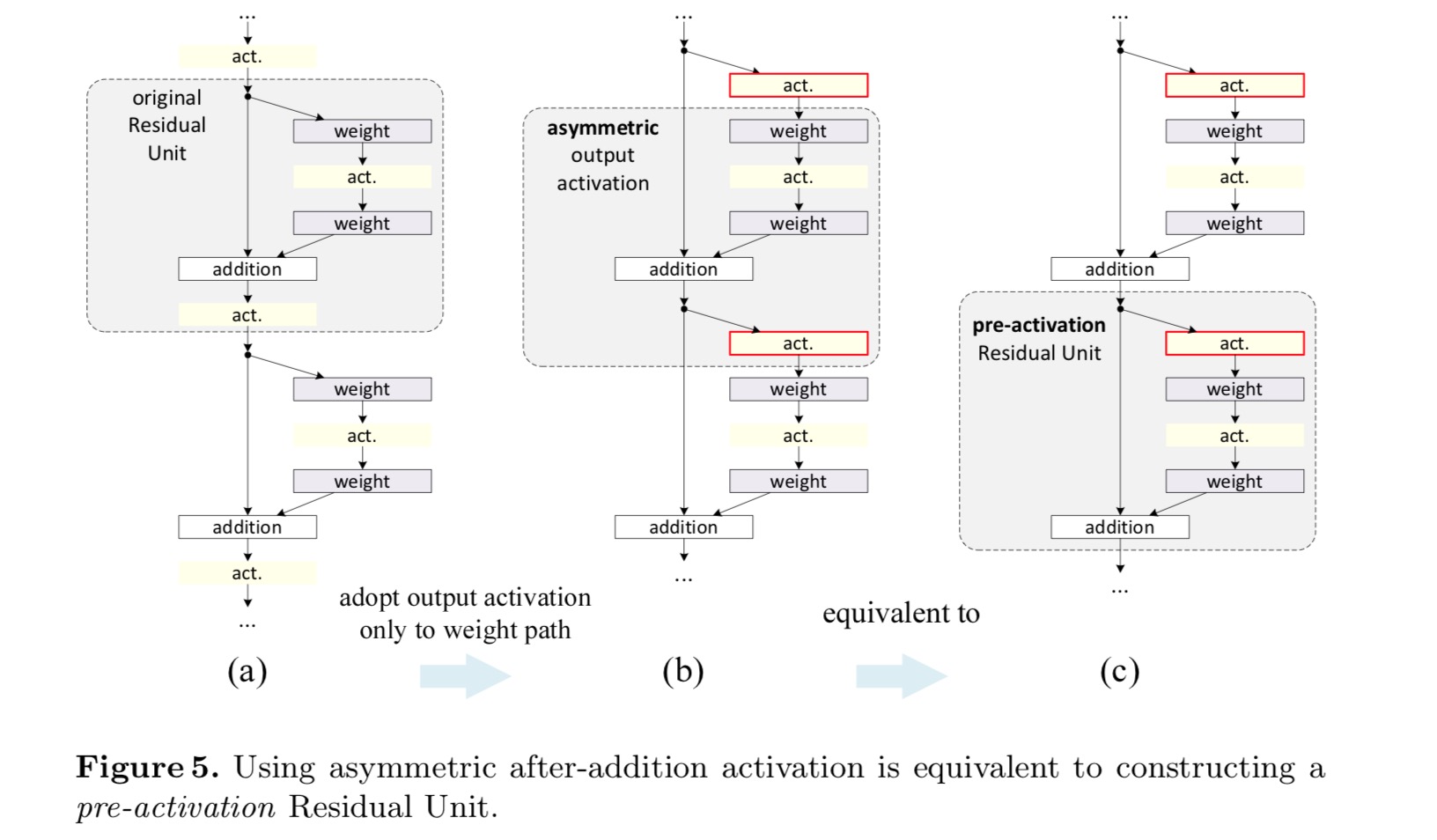
La distinción entre el post-activación/pre-activación es causada por la presencia del elemento sabio adición. Para una red simple que tiene N capas, hay activaciones N – 1 (BN / ReLU), y no importa si pensamos en ellas como activaciones posteriores o previas. Pero para las capas ramificadas fusionadas por adición, la posición de la activación importa. Los diversos usos de la activación se muestran en la Figura 4.
Experimentamos con dos de estos diseños: (1) preactivación de solo ReLU y (2) preactivación completa donde BN y ReLU se adoptan antes de las capas de peso. De alguna manera sorprendente, cuando BN y ReLU se usan como preactivación, los resultados mejoran con márgenes saludables
Encontramos que el impacto de la preactivación es doble. En primer lugar, la optimización se facilita aún más (en comparación con la red de referencia) porque f es una asignación de identidad. En segundo lugar, el uso de BN como preactivación mejora la regularización de los modelos.
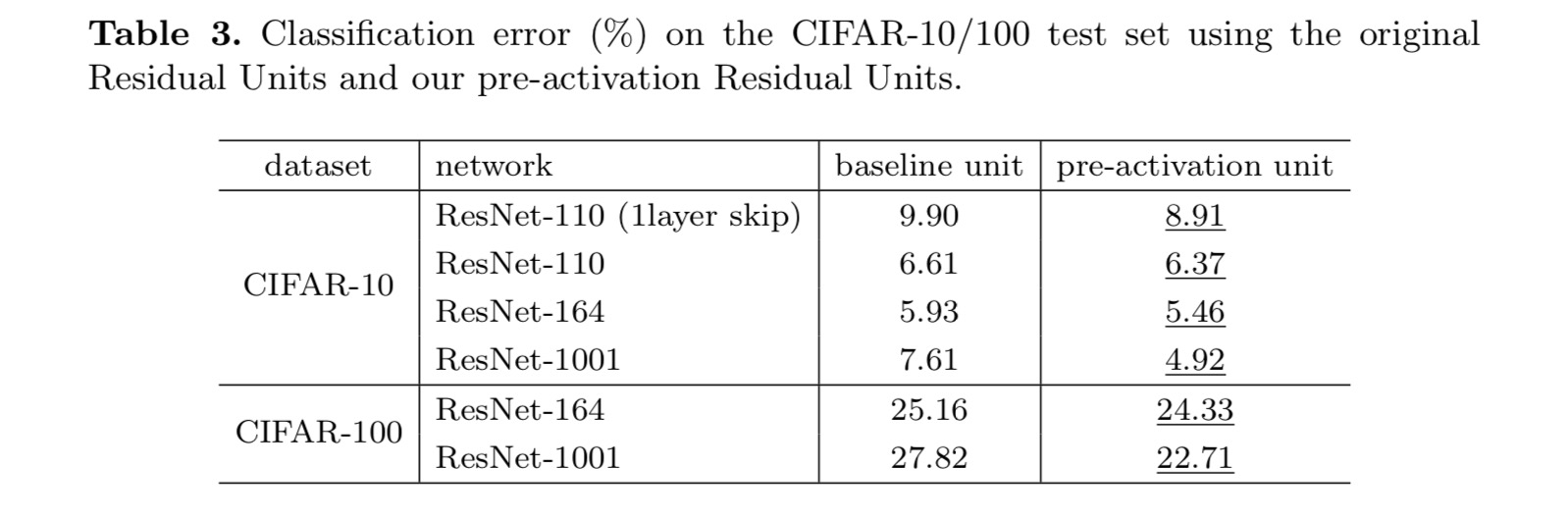
Conclusión
Este artículo investiga las formulaciones de propagación detrás de los mecanismos de conexión de redes residuales profundas. Nuestras derivaciones implican que las conexiones de atajo de identidad y la activación de identidad después de la adición son esenciales para facilitar la propagación de la información. Los experimentos de ablación demuestran fenom-ena que son consistentes con nuestras derivaciones. También presentamos redes profundas de 1000 capas que se pueden entrenar fácilmente y lograr una precisión mejorada.
Transformación Residual Agregada para Redes Neuronales Profundas
Introducción
La investigación sobre reconocimiento visual está experimentando una transición de la «ingeniería de características»a la» ingeniería de redes». El esfuerzo humano se ha desplazado al diseño de mejores arquitecturas de red para las representaciones de aprendizaje.
Diseñar arquitecturas se vuelve cada vez más difícil con el creciente número de hiperparámetros, especialmente cuando hay muchas capas. Las redes VGG exhiben una estrategia simple pero efectiva de construir redes muy profundas: apilar bloques de construcción de la misma forma. Esta estrategia es heredada por redes de red que apilan módulos de la misma topología. Esta regla simple reduce las elecciones libres de los hiper parámetros, y la profundidad se expone como una dimensión esencial en las redes neuronales. Además, argumentamos que la simplicidad de esta regla puede reducir el riesgo de sobreadaptar los hiperparámetros a un conjunto de datos específico. La robustez de las redes y redes de red VGG ha sido probada por varias tareas de reconocimiento visual y por tareas no visuales que involucran el habla y el lenguaje.
A diferencia de las redes VGG, la familia de modelos Inception ha demostrado que las topologías cuidadosamente diseñadas son capaces de lograr una precisión convincente con baja complejidad teórica. Los modelos de inicio han evolucionado con el tiempo, pero una propiedad común importante es una estrategia de transformación dividida y fusión. En un módulo de Inicio, la entrada se divide en unas pocas incrustaciones de dimensiones inferiores (por circunvoluciones de 1×1), transformadas por un conjunto de filtros especializados (3×3, 5×5, etc.), y fusionado por concatenación. Se espera que el comportamiento de transformación dividida y fusión de los módulos Inception se acerque al poder de representación de capas grandes y densas, pero con una complejidad computacional considerablemente menor.
A pesar de la buena precisión, la realización de los modelos Inception ha ido acompañada de una serie de factores que complican la situación. Aunque las combinaciones cuidadosas de estos componentes producen excelentes recetas de redes neuronales, en general no está claro cómo adaptar las arquitecturas de Inicio a nuevos conjuntos de datos/tareas, especialmente cuando hay muchos factores e hiperparámetros que diseñar.
En este artículo, presentamos una arquitectura simple que adopta la estrategia de capas repetitivas de VGG/ResNets, mientras explota la estrategia de transformación dividida y fusión de una manera fácil y extensible. Un módulo en nuestra red realiza un conjunto de transformaciones, cada una en una incrustación de baja dimensión, cuyas salidas se agregan por suma. Perseguimos una realización simple de esta idea: las transformaciones que se agregarán son todas de la misma topología. Este diseño nos permite extendernos a cualquier gran número de transformaciones sin diseños especializados.
Demostramos empíricamente que nuestras transformaciones agregadas superan al módulo ResNet original, incluso bajo la condición restringida de mantener la complejidad computacional y el tamaño del modelo. Enfatizamos que, si bien es relativamente fácil aumentar la precisión aumentando la capacidad (profundizar o ampliar), los métodos que aumentan la precisión mientras mantienen (o reducen) la complejidad son raros en la literatura.
Nuestro método indica que la cardinalidad (el tamaño del conjunto de transformaciones) es una dimensión concreta, medible y de importancia central, además de las dimensiones de anchura y profundidad. Los experimentos demuestran que aumentar la cardinalidad es una forma más efectiva de obtener precisión que ir más profundo o más ancho, especialmente cuando la profundidad y el ancho comienzan a dar rendimientos decrecientes para los modelos existentes.
Nuestras redes neuronales, denominadas ResNeXt (que sugieren la siguiente dimensión), superan a ResNet-101/152, ResNet-200, Inception-v3 y Inception-ResNet-v2 en el conjunto de datos de clasificación de ImageNet. En particular, un ResNeXt de 101 capas puede lograr una mayor precisión que ResNet-200, pero solo tiene un 50% de complejidad. Además, ResNeXt exhibe diseños considerablemente más simples que todos los modelos Inception.
Método
Adoptamos un diseño altamente modular siguiendo VGG / ResNet. Nuestra red consiste en una pila de bloques residuales. Estos bloques tienen la misma topología y están sujetos a dos reglas simples inspiradas en VGG / ResNets: (1) si se producen mapas espaciales del mismo tamaño, los bloques comparten los mismos hiperparámetros (ancho y tamaños de filtro), y (2) cada vez que el mapa espacial se reduce por un factor de 2, el ancho de los bloques se multiplica por un factor de 2. La segunda regla asegura que la complejidad computacional, en términos de FLOPs (operaciones de coma flotante, en #de adiciones múltiples), es aproximadamente la misma para todos los bloques.
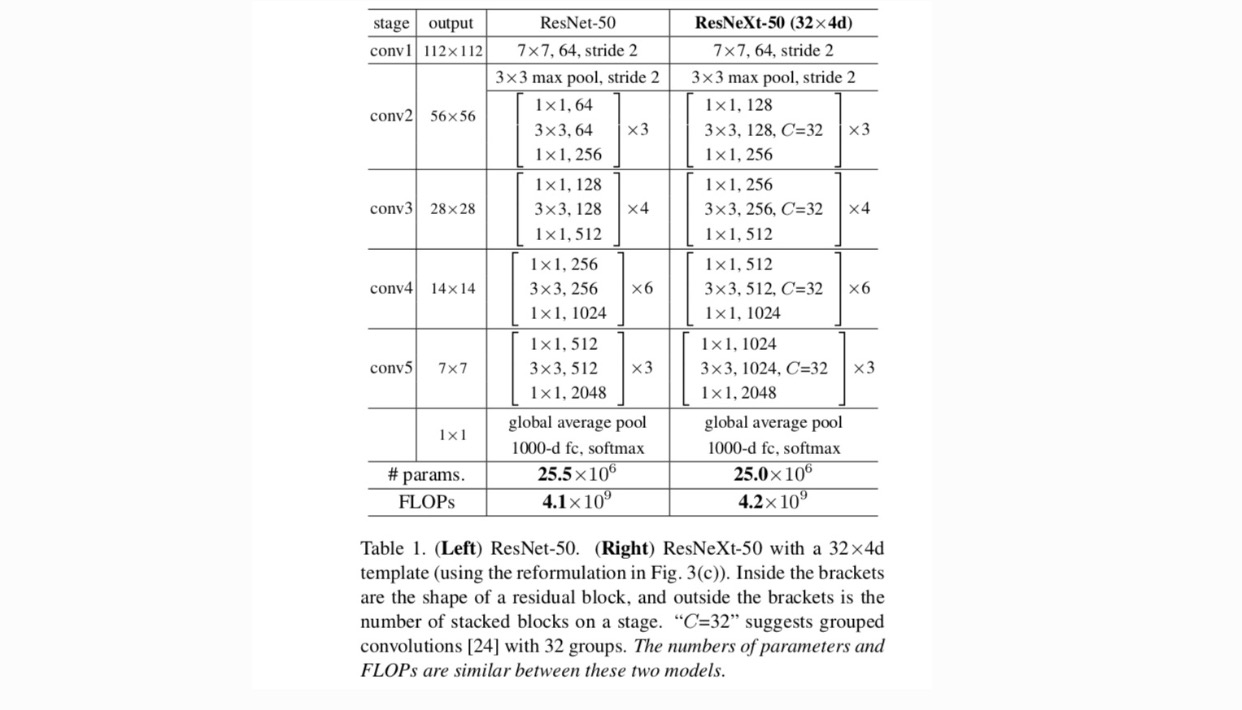
Con estas dos reglas, solo necesitamos diseñar un módulo de plantilla, y todos los módulos de una red se pueden determinar en consecuencia. Por lo tanto, estas dos reglas reducen en gran medida el espacio de diseño y nos permiten centrarnos en algunos factores clave. Las redes construidas por estas reglas se encuentran en la Tabla 1.
Las neuronas más simples en redes neuronales artificiales realizan un producto interno (suma ponderada), que es la transformación elemental realizada por capas convolucionales y completamente conectadas.
La operación anterior se puede refundir como una combinación de división, transformación y agregación. (1): División: el vector se divide como una incrustación de baja dimensión, y en lo anterior, es un subespacio de una sola dimensión (2) Transformación: la representación de baja dimensión se transforma, y en lo anterior, simplemente se escala: (3) Agregación: las transformaciones en todas las incrustaciones se agregan por .
Dado el análisis anterior de una neurona simple, consideramos reemplazar la transformación elemental (w_i, x_i) con una función más genérica, que en sí misma también puede ser una red. Formalmente, presentamos transformaciones agregadas como:
donde puede ser una función arbitraria. Análogo a una neurona simple, debe proyectarse en una incrustación (opcionalmente de baja dimensión) y luego transformarla.
Nos referimos como cardinalidad. está en una posición similar a in, pero no necesita ser igual y puede ser un número arbitrario. Mostramos a través de experimentos que la cardinalidad es una dimensión esencial y puede ser más efectiva que las dimensiones de ancho y profundidad.
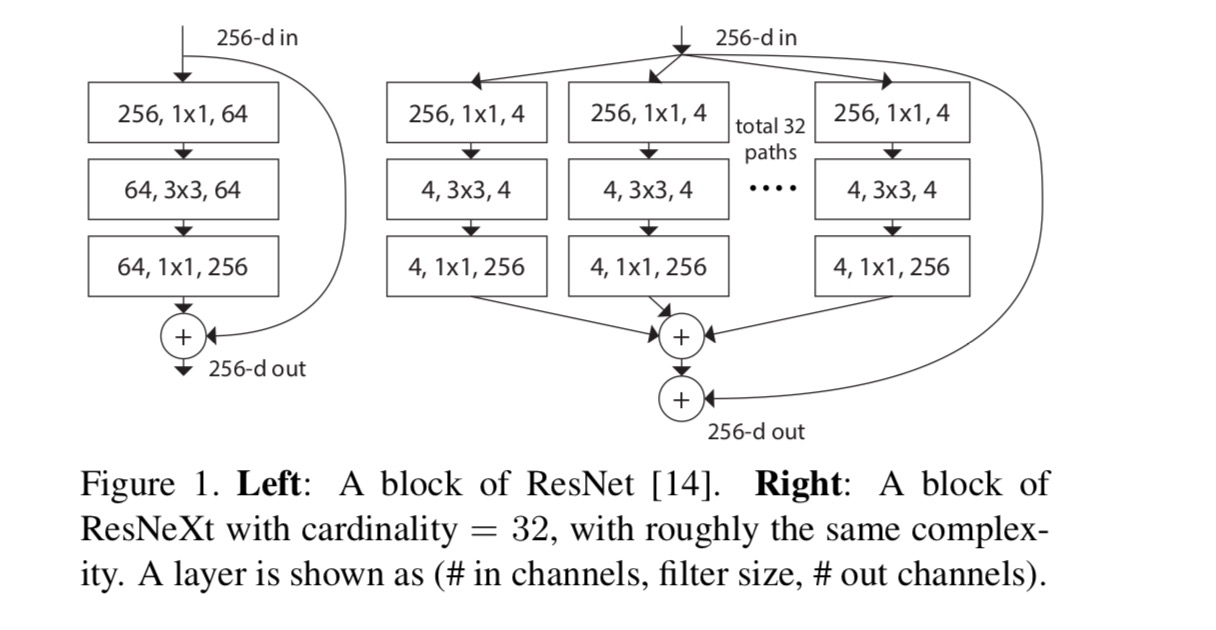
En este trabajo, consideramos una forma sencilla de diseñar las funciones de transformación: todas tienen la misma topología. Esto amplía la estrategia de estilo VGG de repetir capas de la misma forma. Establecemos la transformación individual como la arquitectura en forma de cuello de botella ilustrada en la Fig. 1 (derecha). En este caso, la primera capa de 1×1 en cada uno produce la incrustación de baja dimensión.
La transformación agregada en la última ecuación sirve como función residual:
donde está la salida.
Las relaciones entre ResNeXt y Creación-ResNet/Agrupan-Circunvoluciones se muestra en la siguiente figura:
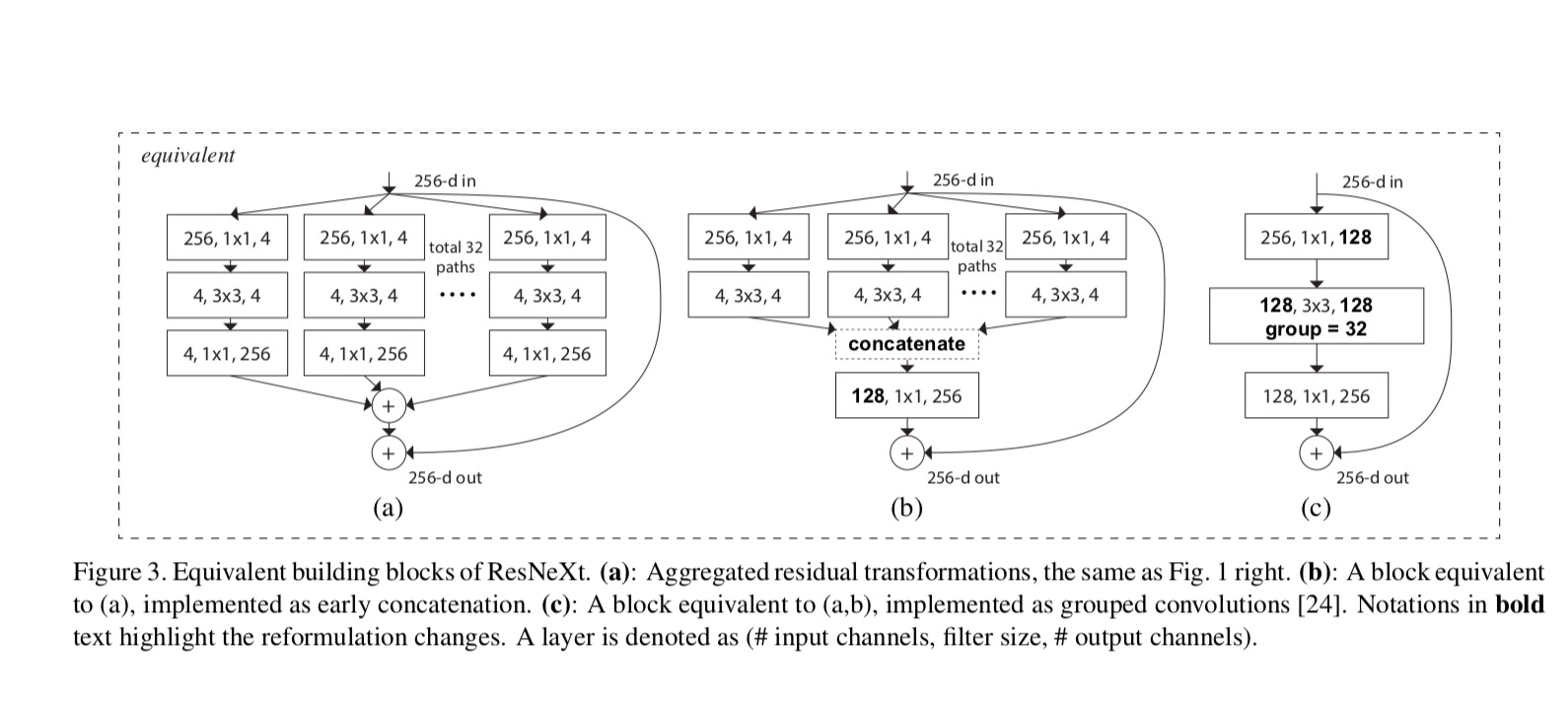
Cuando evaluamos diferentes cardinalidades mientras preservamos la complejidad, queremos minimizar la modificación de otros hiperparámetros. Elegimos ajustar el ancho del cuello de botella (por ejemplo, 4-d en la Figura 1(derecha)), porque se puede aislar de la entrada y salida del bloque. Esta estrategia no introduce cambios en otros hiperparámetros (profundidad o ancho de entrada/salida de bloques), por lo que es útil para nosotros enfocarnos en el impacto de la cardinalidad.
En la Fig. 1 (izquierda), el bloque de cuello de botella de ResNet original tiene parámetros y FLOPs proporcionales (en el mismo tamaño de mapa de entidades). Con ancho de cuello de botella, nuestra plantilla en la Fig. 1 (derecha) tiene: parámetros y FLOPs proporcionales. Cuando y, este número . La siguiente tabla muestra la relación entre cardinalidad y ancho de cuello de botella .

Experimentos
Cardinalidad vs Ancho. En primer lugar, evaluamos el equilibrio entre la cardinalidad y el ancho del cuello de botella, bajo la complejidad preservada, como se muestra en la Tabla 2. La tabla 3 muestra los resultados. En comparación con ResNet-50, el ResNeXt-50 de 32×4d tiene un error de validación del 22,2%, que es un 1,7% inferior al 23,9% de la línea de base de ResNet. Con el aumento de la cardinalidad de 1 a 32 mientras se mantiene la complejidad, la tasa de error sigue reduciéndose. Además, el ResNeXt 32×4d también tiene un error de entrenamiento mucho menor que el ResNet countetpart, lo que sugiere que las ganancias no provienen de la regularización, sino de representaciones más fuertes.
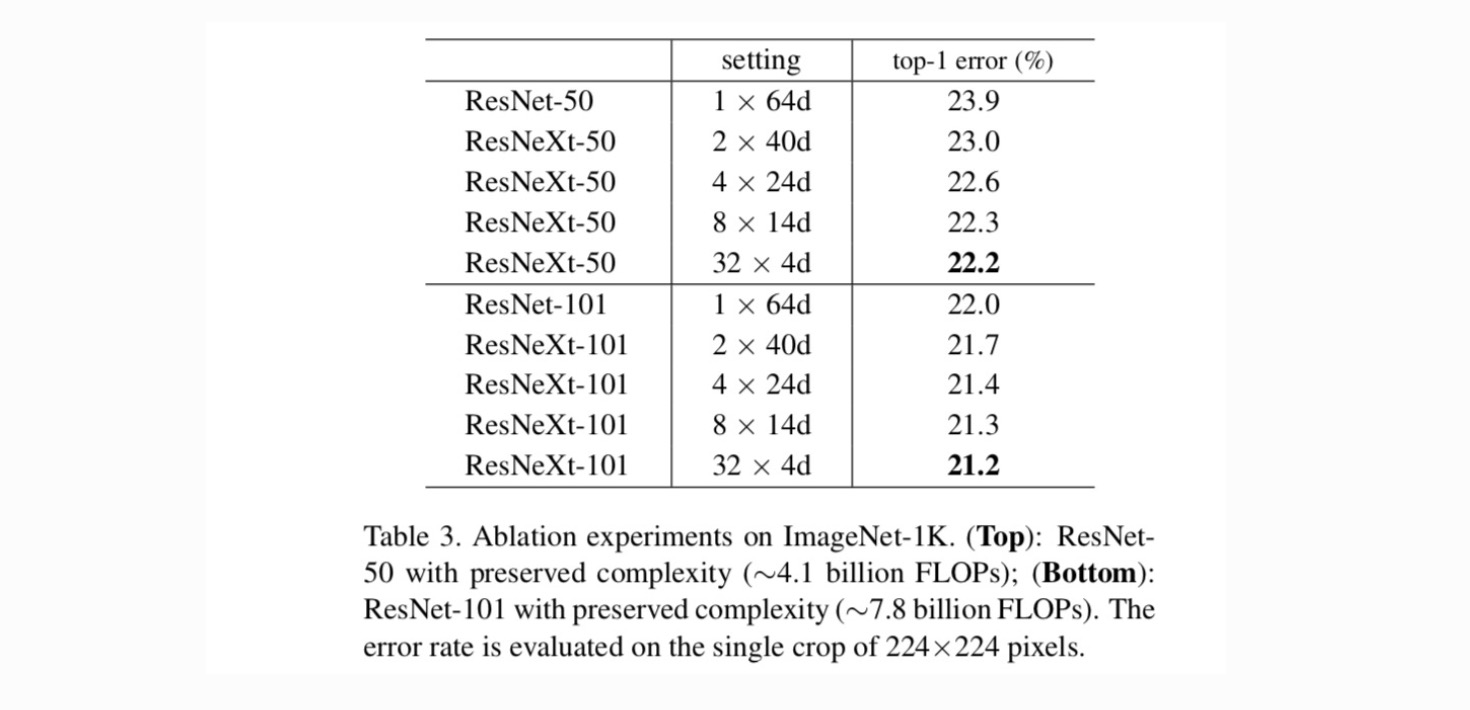
Aumento de la Cardinalidad vs. Más Profundo / más ancho.
A continuación investigamos el aumento de la complejidad aumentando la cardinalidad C o aumentando la profundidad o el ancho. Comparamos las siguientes variantes (1) Que van más profundo a 200 capas. Adoptamos la ResNet-200. (2) Se ensancha aumentando el ancho del cuello de botella. (3) Aumento de la cardinalidad duplicando C.
La tabla 4 muestra que el aumento de la complejidad en 2× reduce de manera consistente el error en comparación con la línea de base ResNet-101 (22,0%). Pero la mejora es pequeña cuando se va más profundo (ResNet-200, en un 0,3%) o más amplio (ResNet-101 más amplio, en un 0,7%). Por el contrario, el aumento de la cardinalidad C muestra resultados mucho mejores que ir más profundo o más amplio.
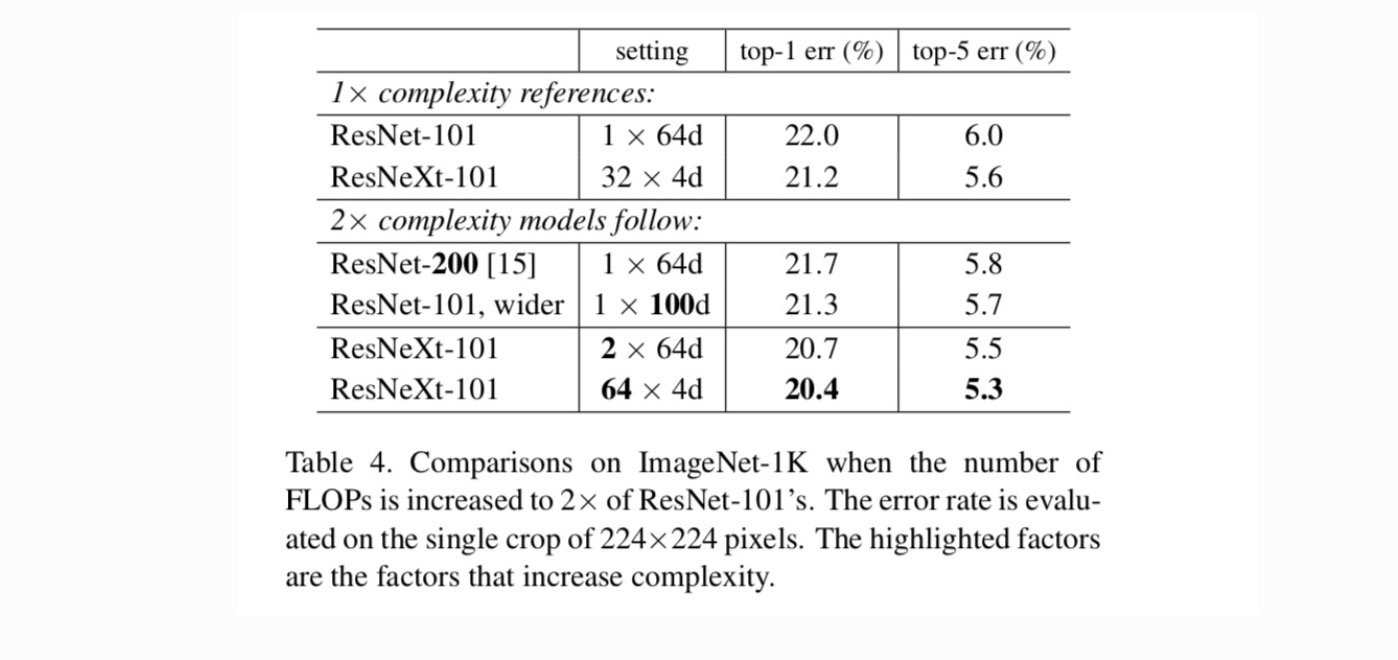
Comparaciones con resultados de última generación. La tabla 5 muestra más resultados de las pruebas de un solo cultivo en el conjunto de validación de ImageNet. Nuestros resultados se comparan favorablemente con ResNet, Inception-v3/v4 y Inception-ResNet-v2, logrando una tasa de error de 5 primeros cultivos del 4,4%. Además, nuestro diseño de arquitectura es mucho más simple que todos los modelos Inception, y requiere considerablemente menos hiperparámetros que se establezcan a mano.
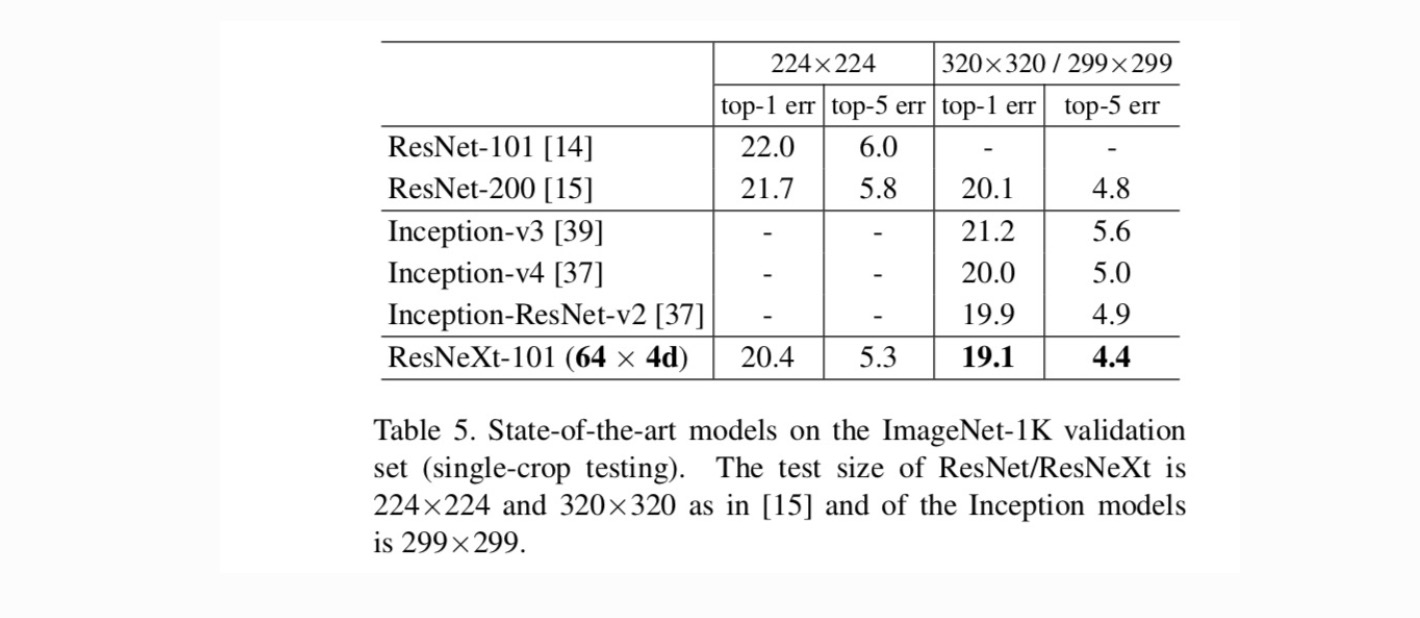
temas Más