Introducción a la Estimación de Movimiento con Flujo Óptico

En este tutorial, profundizamos en los fundamentos del Flujo Óptico, analizamos algunas de sus aplicaciones e implementamos sus dos variantes principales (dispersa y densa). También discutimos brevemente los enfoques más recientes que utilizan el aprendizaje profundo y las direcciones futuras prometedoras.

Los recientes avances en la investigación de la visión por computadora han permitido a las máquinas percibir su mundo circundante a través de técnicas como la detección de objetos para detectar instancias de objetos que pertenecen a una determinada clase y la segmentación semántica para la clasificación en píxeles.

Sin embargo, para procesar entradas de vídeo en tiempo real, la mayoría de las implementaciones de estas técnicas solo abordan relaciones de objetos dentro del mismo fotograma \(x, y)\) sin tener en cuenta la información de tiempo \(t)\). En otras palabras, reevaluan cada fotograma de forma independiente, como si fueran imágenes completamente no relacionadas, para cada ejecución. Sin embargo, ¿qué pasa si necesitamos las relaciones entre fotogramas consecutivos, por ejemplo, queremos rastrear el movimiento de los vehículos a través de fotogramas para estimar su velocidad actual y predecir su posición en el siguiente fotograma?

O, alternativamente, ¿qué pasa si requerimos información sobre las relaciones de postura humana entre fotogramas consecutivos para reconocer acciones humanas como tiro con arco, béisbol y baloncesto?

En este tutorial, aprenderemos qué es el flujo óptico, cómo implementar sus dos variantes principales (disperso y denso), y también obtendremos una visión general de los enfoques más recientes que involucran aprendizaje profundo y direcciones futuras prometedoras.

¿Qué es el flujo óptico?
Implementación de Flujo Óptico Disperso
Implementación de Flujo Óptico Denso
Aprendizaje profundo y más allá

¿Qué es el flujo óptico?

Comencemos con una comprensión de alto nivel del flujo óptico. El flujo óptico es el movimiento de objetos entre fotogramas consecutivos de secuencia, causado por el movimiento relativo entre el objeto y la cámara. El problema del flujo óptico puede expresarse como:

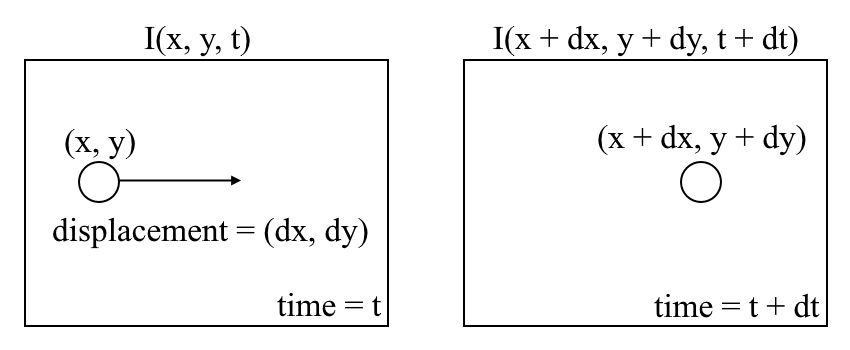
donde entre fotogramas consecutivos, podemos expresar la intensidad de imagen \((I)\) en función del espacio \((x, y)\) y tiempo \((t)\). En otras palabras, si tomamos la primera imagen \(I(x, y, t)\) y el movimiento de sus píxeles por \((dx, dy)\) a través de \(t\) tiempo, obtenemos la nueva imagen \(I(x + dx, y + dy, t + dt)\).

En primer lugar, asumimos que las intensidades de píxeles de un objeto son constantes entre fotogramas consecutivos.

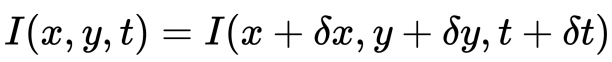
En segundo lugar, tomamos la Aproximación de la serie de Taylor del RHS y eliminamos los términos comunes.

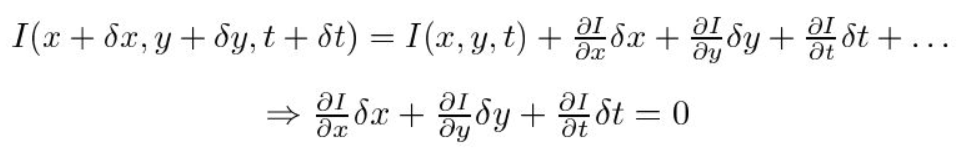
En tercer lugar, dividimos por \(dt\) para derivar la ecuación de flujo óptico:

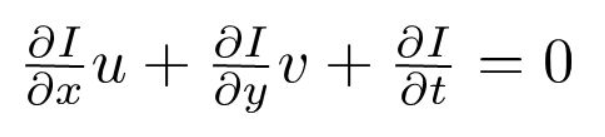
donde \(u = dx/dt\) y \(v = dy/dt\).

\(dI / dx, dI/dy\) y \(dI / dt\) son los degradados de imagen a lo largo del eje horizontal, el eje vertical y el tiempo. Por lo tanto, concluimos con el problema del flujo óptico, es decir, resolver \(u (dx/dt)\) y \(v (dy/dt)\) para determinar el movimiento a lo largo del tiempo. Puede notar que no podemos resolver directamente la ecuación de flujo óptico para \(u\) y \(v\) ya que solo hay una ecuación para dos variables desconocidas. Implementaremos algunos métodos como el método Lucas-Kanade para abordar este problema.

Flujo óptico Disperso vs Denso

El flujo óptico disperso proporciona los vectores de flujo de algunas «características interesantes» (por ejemplo, unos pocos píxeles que representan los bordes o esquinas de un objeto) dentro del marco, mientras que el flujo óptico denso, que proporciona los vectores de flujo de todo el marco (todos los píxeles), hasta un vector de flujo por píxel. Como habrías adivinado, el flujo óptico denso tiene una mayor precisión a costa de ser lento/costoso computacionalmente.

Implementar Flujo óptico Disperso

Flujo óptico disperso selecciona un conjunto de características dispersas de píxeles (por ejemplo, características interesantes como bordes y esquinas) para rastrear sus vectores de velocidad (movimiento). Las características extraídas se pasan en la función de flujo óptico de cuadro a cuadro para garantizar que se rastreen los mismos puntos. Hay varias implementaciones de flujo óptico escaso, incluido el método Lucas–Kanade, el método Horn–Schunck, el método Buxton–Buxton y más. Utilizaremos el método Lucas-Kanade con OpenCV, una biblioteca de código abierto de algoritmos de visión artificial, para su implementación.

Configurar su entorno

Si aún no tiene OpenCV instalado, abra Terminal y ejecute:

pip install opencv-python

Ahora, clone el repositorio del tutorial ejecutando:

git clone https://github.com/chuanenlin/optical-flow.git

sparse-starter.py con tu editor de texto. Escribiremos todo el código en este archivo Python.

Configurar OpenCV para leer un vídeo y configurar parámetros

Detector de esquinas Shi-Tomasi: seleccionar los píxeles para rastrear

Para la implementación de flujo óptico escaso, solo rastreamos el movimiento de un conjunto de características de píxeles. Las características de las imágenes son puntos de interés que presentan información rica en contenido de imagen. Por ejemplo, tales características pueden ser puntos en la imagen que son invariantes a la traducción, escala, rotación y cambios de intensidad, como esquinas.

El Detector de esquinas Shi-Tomasi es muy similar al popular Detector de Esquinas Harris, que se puede implementar mediante los siguientes tres procedimientos:

1. Determinar ventanas (parches de imagen pequeños) con gradientes grandes (variaciones en la intensidad de la imagen) cuando se traduce en las direcciones \(x\) e \(y\).
2. Para cada ventana, calcule una partitura \(R\).
3. Dependiendo del valor de \(R\), cada ventana se clasifica como plana, de borde o de esquina.

Si desea obtener más información sobre una explicación matemática paso a paso del Detector Harris Corner, no dude en revisar estas diapositivas.

Shi y Tomasi más tarde hicieron una pequeña pero efectiva modificación al Detector de esquinas Harris en su papel Good Features to Track.

La modificación es la ecuación en la que se calcula la puntuación \(R\). En el Detector de Esquinas Harris, la función de puntuación viene dada por:

$$
\begin{array}{c}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\newline \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\end{array}
$$

en su Lugar, Shi-Tomasi propuesto la función de puntuación como:

$$
R=\min \left(\lambda_{1}, \lambda_{2}\right)
$$

lo que básicamente significa que si \(R\) es mayor que un umbral, se clasifica como una esquina. A continuación se comparan las funciones de puntuación de Harris (izquierda) y Shi-Tomasi (derecha) en el espacio \(λ1-λ2\).

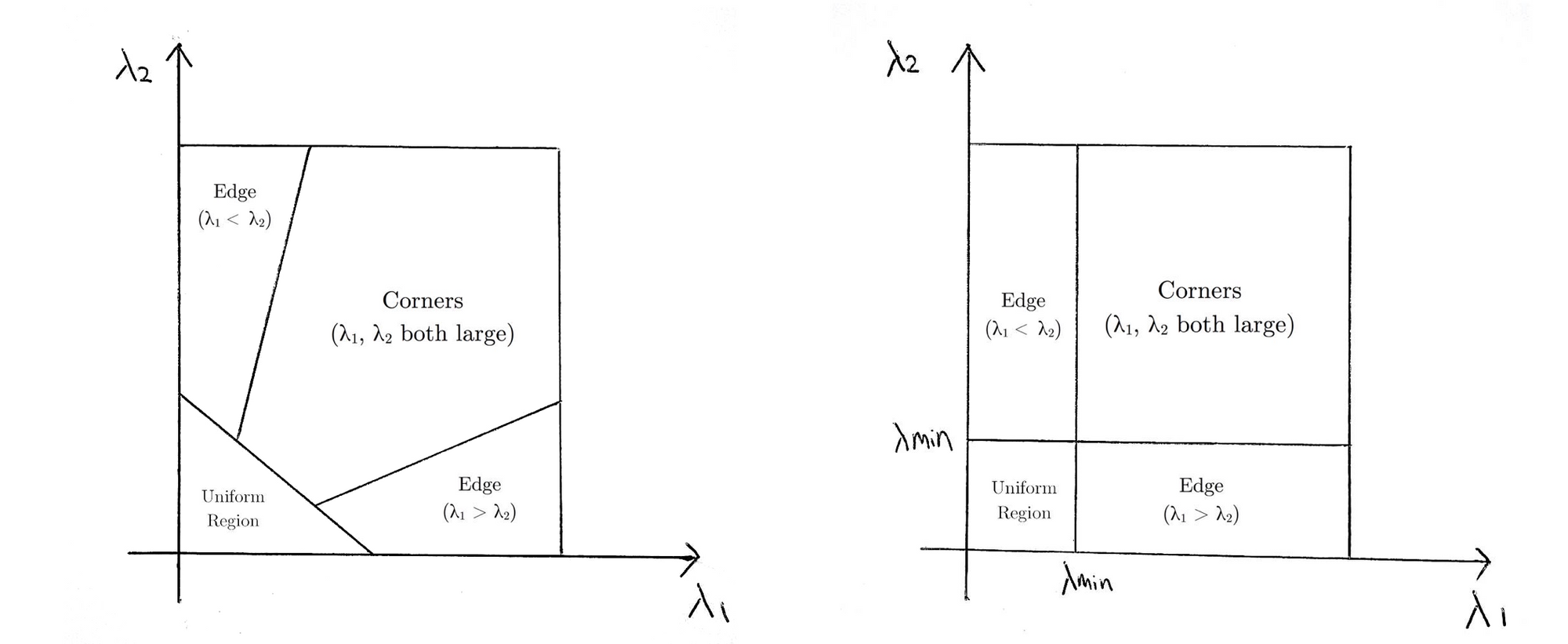
Para Shi-Tomasi, solo cuando \(λ1\) y \(λ2\) están por encima de un umbral mínimo \(λmin\) se clasifica la ventana como esquina.

La documentación de la implementación de OpenCV de Shi-Tomasi via goodFeaturesToTrack() se puede encontrar aquí.

Seguimiento de objetos específicos

Puede haber escenarios en los que solo desee rastrear un objeto de interés específico (por ejemplo, rastrear a cierta persona) o una categoría de objetos (como todos los vehículos de 2 ruedas en tráfico). Puede modificar fácilmente el código para rastrear los píxeles de los objetos que desee cambiando la variable prev.

También puede combinar la detección de objetos con este método para estimar solo el flujo de píxeles dentro de los cuadros delimitadores detectados. De esta manera, puede realizar un seguimiento de todos los objetos de un tipo o categoría en particular en el vídeo.

Lucas-Kanade: Flujo Óptico Escaso

Lucas y Kanade propusieron una técnica eficaz para estimar el movimiento de características interesantes comparando dos fotogramas consecutivos en su artículo Una Técnica de Registro de Imágenes Iterativas con una Aplicación a la Visión Estéreo. El método Lucas-Kanade funciona bajo los siguientes supuestos:

1. Dos fotogramas consecutivos están separados por un pequeño incremento de tiempo (\(dt\)) de modo que los objetos no se desplazan significativamente (en otras palabras, el método funciona mejor con objetos de movimiento lento).
2. Un marco retrata una escena «natural» con objetos texturizados que exhiben tonos de gris que cambian suavemente.

Primero, bajo estas suposiciones, podemos tomar una pequeña ventana de 3×3 (vecindario) alrededor de las características detectadas por Shi-Tomasi y asumir que los nueve puntos tienen el mismo movimiento.

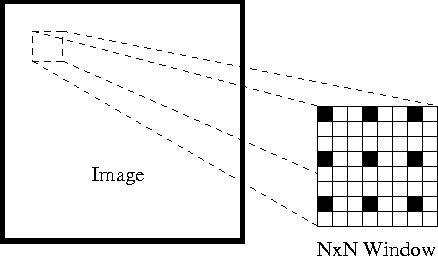
Esto puede representarse como

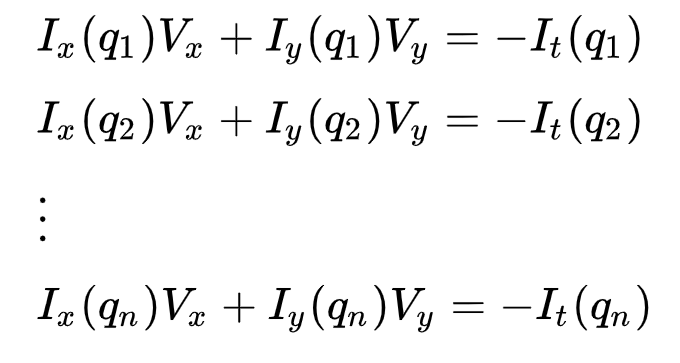
donde \(q_1, q_2, q, q_n\) denotan los píxeles dentro de la ventana (por ejemplo, \(n\) = 9 para una ventana de 3×3) y \(I_x(q_i)\), \(I_y(q_i)\), y \(I_t(q_i)\) denotan las derivadas parciales de la imagen \(I\) con respecto a la posición \((x, y)\) y time \(t\), para pixel \(q_i\) en el momento actual.

Esto es solo la Ecuación de Flujo Óptico (que describimos anteriormente) para cada uno de los n píxeles.

El conjunto de ecuaciones se puede representar en la siguiente forma de matriz donde \(Av = b\):

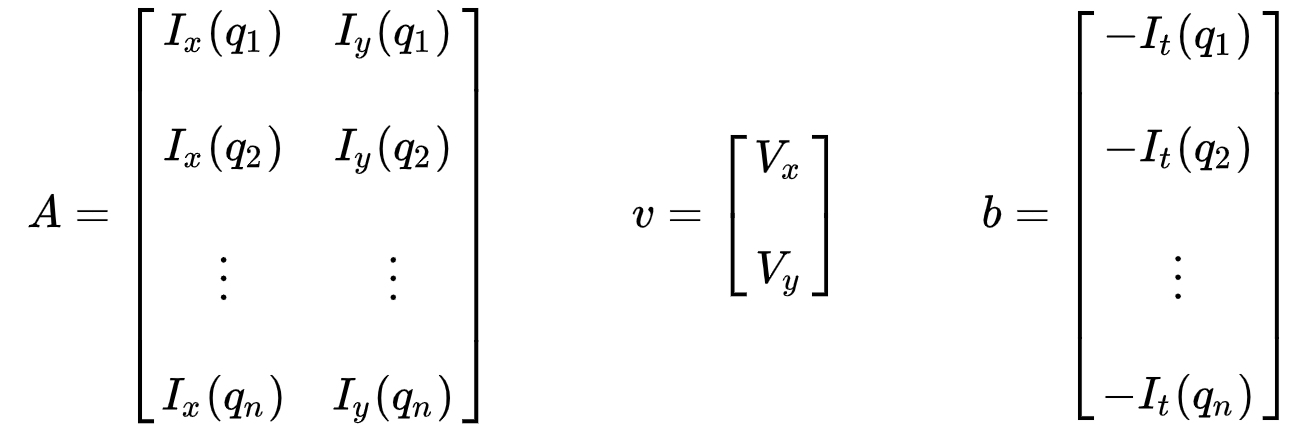
Tenga en cuenta que anteriormente (ver «¿Qué es el flujo óptico?»sección), nos enfrentamos al problema de tener que resolver dos variables desconocidas con una ecuación. Ahora nos enfrentamos a tener que resolver dos incógnitas (\(V_x\) y \(V_y\)) con nueve ecuaciones, lo que está sobre determinado.

En segundo lugar, para abordar el problema sobre determinado, aplicamos el ajuste de mínimos cuadrados para obtener el siguiente problema de dos ecuaciones-dos desconocidas:

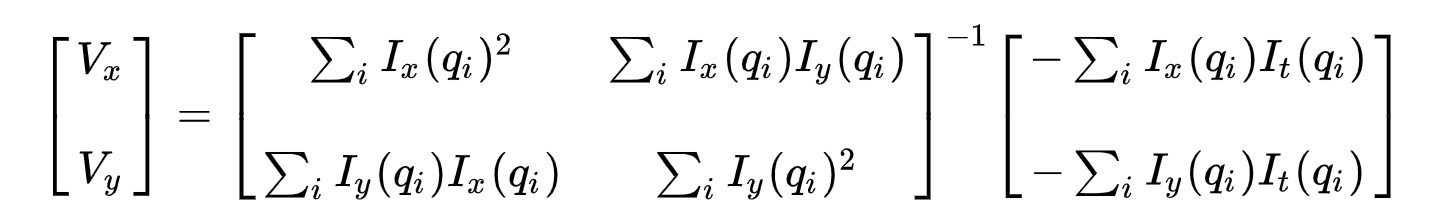
donde \(Vx = u = dx/dt\) denota el movimiento de \(x\) a lo largo del tiempo y \(Vy = v = dy/dt\) denota el movimiento de y a lo largo del tiempo. La resolución de las dos variables completa el problema de flujo óptico.

En pocas palabras, identificamos algunas características interesantes para rastrear y calcular iterativamente los vectores de flujo óptico de estos puntos. Sin embargo, adoptar el método Lucas-Kanade solo funciona para movimientos pequeños (a partir de nuestra suposición inicial) y falla cuando hay movimiento grande. Por lo tanto, la implementación OpenCV del método Lucas-Kanade adopta pirámides.

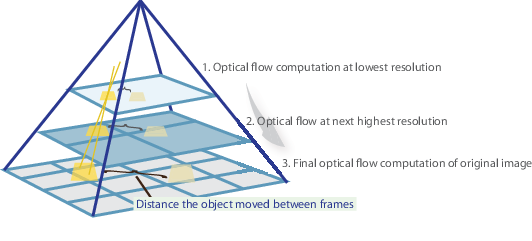
En una vista de alto nivel, los movimientos pequeños se descuidan a medida que subimos por la pirámide y los movimientos grandes se reducen a movimientos pequeños: calculamos el flujo óptico junto con la escala. Una explicación matemática completa de la implementación de OpenCV se puede encontrar en las notas de Bouguet y la documentación de la implementación de OpenCV del método Lucas-Kanade a través de calcOpticalFlowPyrLK() se puede encontrar aquí.

Visualizando

Y eso es todo! Abra el terminal y ejecute

python sparse-starter.py

para probar su implementación de flujo óptico disperso.

En caso de que haya perdido algún código, el código completo se puede encontrar en sparse-solution.py.

Implementando Flujo Óptico Denso

Previamente hemos calculado el flujo óptico para un conjunto de características dispersas de píxeles. Flujo óptico denso intenta calcular el vector de flujo óptico para cada píxel de cada fotograma. Si bien tal cálculo puede ser más lento, da un resultado más preciso y un resultado más denso adecuado para aplicaciones como la estructura de aprendizaje a partir del movimiento y la segmentación de video. Hay varias implementaciones de flujo óptico denso. Utilizaremos el método Farneback, una de las implementaciones más populares, con el uso de OpenCV, una biblioteca de código abierto de algoritmos de visión artificial, para la implementación.

Configuración de su entorno

Si aún no lo ha hecho, siga el paso 1 de implementación de flujo óptico disperso para configurar su entorno.

Siguiente, abierto dense-starter.py con tu editor de texto. Escribiremos todo el código en este archivo Python.

Configurar OpenCV para leer un vídeo

Flujo óptico de Farneback

Gunnar Farneback propuso una técnica eficaz para estimar el movimiento de características interesantes comparando dos fotogramas consecutivos en su artículo Estimación de Movimiento de Dos Fotogramas Basada en la Expansión Polinómica.

En primer lugar, el método se aproxima a las ventanas (vea la sección de Lucas Kanade de implementación de flujo óptico disperso para más detalles) de los marcos de imagen por polinomios cuadráticos a través de la transformación de expansión polinómica. En segundo lugar, observando cómo el polinomio se transforma bajo traslación (movimiento), se define un método para estimar los campos de desplazamiento a partir de coeficientes de expansión polinómica. Después de una serie de refinamientos, se calcula el flujo óptico denso. El artículo de Farneback es bastante conciso y sencillo de seguir, por lo que recomiendo revisar el artículo si desea una mayor comprensión de su derivación matemática.

Para la implementación de OpenCV, calcula la magnitud y la dirección del flujo óptico a partir de una matriz de vectores de flujo de 2 canales \((dx/dt, dy/dt)\), el problema de flujo óptico. A continuación, visualiza el ángulo (dirección) del flujo por tono y la distancia (magnitud) del flujo por valor de la representación de color HSV. La resistencia del HSV siempre se establece en un máximo de 255 para una visibilidad óptima. La documentación de la implementación de OpenCV del método Farneback a través de calcOpticalFlowFarneback() se puede encontrar aquí.

Visualizando

Y eso es todo! Abra el terminal y ejecute

python dense-starter.py

para probar su implementación de flujo óptico denso.

En caso de que haya perdido algún código, el código completo se puede encontrar en dense-solution.py.

Flujo óptico mediante aprendizaje profundo

Aunque el problema del flujo óptico ha sido históricamente un problema de optimización, los enfoques recientes mediante la aplicación de aprendizaje profundo han demostrado resultados impresionantes. En general, estos enfoques toman dos fotogramas de vídeo como entrada para emitir el flujo óptico (imagen codificada por colores), que puede expresarse como:

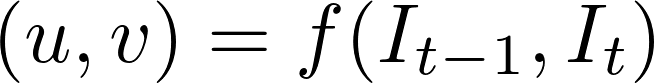
donde \(u\) es el movimiento en la dirección \(x\), \(v\) es el movimiento en la dirección \(y\), y \(f\) es una red neuronal que toma dos fotogramas consecutivos \(I_{t-1}\) (fotograma a la vez = \(t-1)\) y \(I_t\) (fotograma a la vez = \(t)\) como entrada.

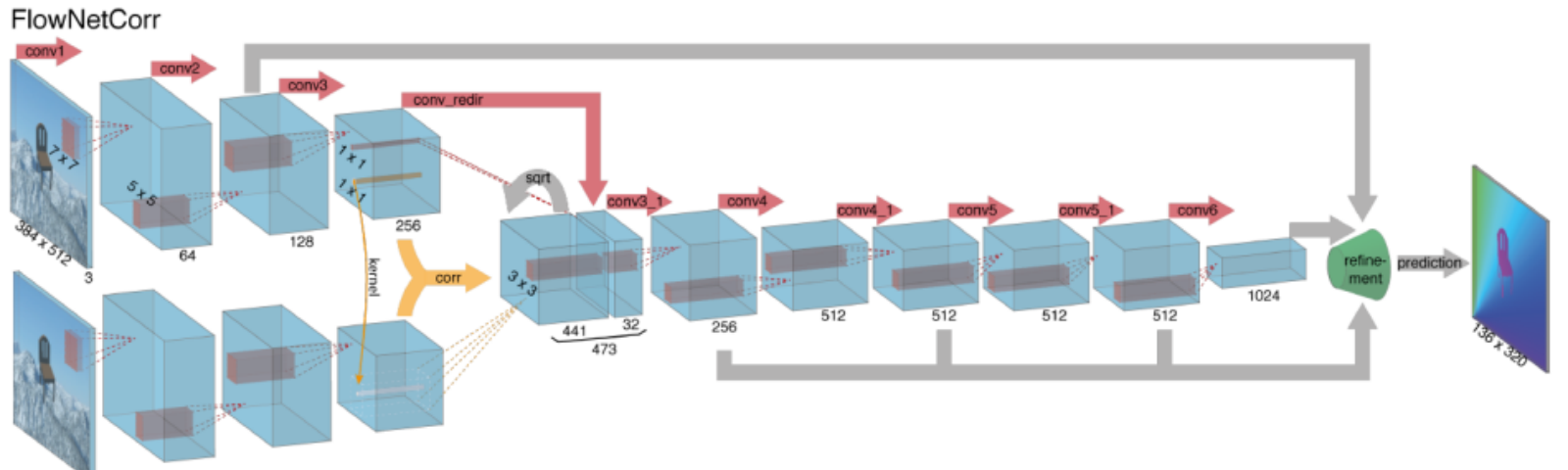
La computación de flujo óptico con redes neuronales profundas requiere grandes cantidades de datos de entrenamiento, lo que es particularmente difícil de obtener. Esto se debe a que el etiquetado de secuencias de vídeo para el flujo óptico requiere determinar con precisión el movimiento exacto de todos y cada uno de los puntos de una imagen con precisión de subpíxeles. Para abordar el tema del etiquetado de los datos de entrenamiento, los investigadores utilizaron gráficos por computadora para simular mundos realistas masivos. Dado que los mundos son generados por instrucción, se conoce el movimiento de todos y cada uno de los puntos de una imagen en una secuencia de video. Algunos ejemplos de esto incluyen MPI-Sintel, una película CGI de código abierto con etiquetado de flujo óptico renderizado para varias secuencias, y Flying Chairs, un conjunto de datos de muchas sillas que vuelan a través de fondos aleatorios también con etiquetado de flujo óptico.

Resolver problemas de flujo óptico con aprendizaje profundo es un tema extremadamente candente en este momento, con variantes de FlowNet, SpyNet, PWC-Net y más, cada una con un rendimiento superior en varios puntos de referencia.

Aplicación de flujo óptico: Segmentación semántica

El campo de flujo óptico es una vasta mina de información para la escena observada. A medida que mejoran las técnicas para determinar con precisión el flujo óptico, es interesante ver aplicaciones de flujo óptico en unión con varias otras tareas fundamentales de visión por computadora. Por ejemplo, la tarea de la segmentación semántica es dividir una imagen en series de regiones correspondientes a clases de objetos únicas, pero los objetos colocados de cerca con texturas idénticas a menudo son difíciles para las técnicas de segmentación de fotogramas individuales. Sin embargo, si los objetos se colocan por separado, los movimientos distintos de los objetos pueden ser muy útiles cuando la discontinuidad en el campo de flujo óptico denso corresponde a los límites entre los objetos.

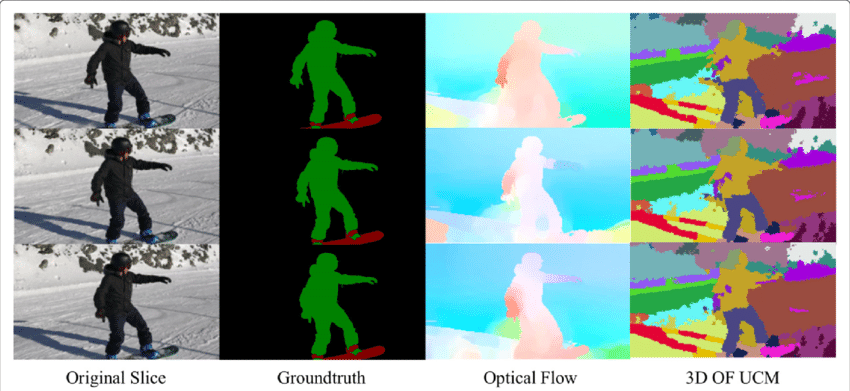
Aplicación de flujo óptico: Detección de objetos & Seguimiento

Otra aplicación prometedora del flujo óptico puede ser con detección y seguimiento de objetos o, en una forma de alto nivel, hacia la construcción de sistemas de seguimiento y análisis de tráfico de vehículos en tiempo real. Dado que el flujo óptico disperso utiliza el seguimiento de puntos de interés, tales sistemas en tiempo real pueden realizarse mediante técnicas de flujo óptico basadas en características desde una cámara estacionaria o cámaras conectadas a vehículos.

Conclusión

Fundamentalmente, los vectores ópticos de flujo funcionan como entrada a una miríada de tareas de alto nivel que requieren comprensión de escenas de secuencias de video, mientras que estas tareas pueden actuar como bloques de construcción para sistemas aún más complejos, como el análisis de expresión facial, la navegación autónoma de vehículos y mucho más. Las nuevas aplicaciones para el flujo óptico aún por descubrir están limitadas solo por el ingenio de sus diseñadores.

Perezoso para codificar, ¿no quiere gastar en GPU? Dirígete a Nanonets y construye modelos de visión por computadora de forma gratuita.