sin Supervisión de Inferencia Bayesiana (reducción de dimensiones y desenterrando características)
Bajo nivel de la característica de detección de uso de bordes

Finalmente, el momento que todos hemos estado esperando, el siguiente en nuestra supervisión inferencia Bayesiana de la serie: Nuestra (o no tanto) inmersión profunda en el Operador de Sobel.
Un algoritmo de detección de bordes verdaderamente mágico, permite la extracción de características de bajo nivel y la reducción de dimensionalidad, reduciendo esencialmente el ruido en la imagen. Ha sido particularmente útil en aplicaciones de reconocimiento facial.
El hijo amoroso de 1968 de Irwin Sobel y Gary Feldman (Laboratorio de Inteligencia Artificial de Stanford), este algoritmo fue la inspiración de muchas técnicas modernas de detección de bordes. Al enrollar dos núcleos o máscaras opuestas sobre una imagen dada (p. ej. ver abajo a la izquierda) (cada uno capaz de detectar bordes horizontales o verticales), podemos crear una representación menos ruidosa y suavizada (ver abajo a la derecha).
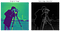
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel valores (generalmente luminancia) diferenciando la diferencia entre cada píxel (el píxel de anclaje) y sus píxeles circundantes (esencialmente aproximándose a la derivada de una imagen).
Esto da como resultado suavizar la imagen original y producir una salida de menor dimensión, donde las características geométricas de bajo nivel se pueden ver más claramente. Estas salidas se pueden usar como entradas en algoritmos de clasificación más complejos, o como ejemplos utilizados para la agrupación probabilística no supervisada a través de Divergencia Kullback-Leibler (KLD) (como se ve en mi blog reciente en LBP).
Generar nuestra salida de dimensión inferior requiere que tomemos la derivada de la imagen. Primero, calculamos el derivado en las direcciones x e y. Creamos dos núcleos de 3×3 (ver matrices), con ceros a lo largo del centro del eje correspondiente, dos en los cuadrados centrales perpendiculares al cero central y unos en cada una de las esquinas. Cada uno de los valores distintos de cero debe ser positivo en la parte superior/a la derecha de los ceros (dependiendo del eje) y negativo en su lado correspondiente. Estos núcleos se denominan Gx y Gy.
Aparecen en el formato:
Estos núcleos, a continuación, convolución sobre nuestra imagen, la colocación de la central de píxeles de cada núcleo de cada píxel en la imagen. Utilizamos la multiplicación de matrices para calcular el valor de intensidad de un nuevo píxel correspondiente en una imagen de salida, para cada núcleo. Por lo tanto, terminamos con dos imágenes de salida (una para cada dirección cartesiana).
El objetivo es encontrar la diferencia/cambio entre el píxel de la imagen y todos los píxeles de la matriz de degradado (núcleo) (Gx y Gy). Más matemáticamente, esto se puede expresar como.
Nota al margen:
Técnicamente no estamos enredando nada. Aunque nos gusta referirnos a’ convoluciones ‘ en círculos de IA y aprendizaje automático, una convolución implicaría voltear la imagen original. Matemáticamente hablando, cuando nos referimos a las circunvoluciones, realmente estamos calculando la correlación cruzada entre cada área de 3×3 de la entrada y la máscara para cada píxel. La imagen de salida es la covarianza general entre la máscara y la entrada. Así es como se detectan los bordes.
De vuelta a nuestra explicación de Sobel
Los valores calculados para cada multiplicación de matrices entre la máscara y la sección 3×3 de la entrada se suman para producir el valor final para el píxel en la imagen de salida. Esto genera una nueva imagen que contiene información sobre la presencia de bordes verticales y horizontales presentes en la imagen original. Esta es una representación geométrica de la imagen original. Además, como se garantiza que este operador produzca la misma salida cada vez, esta técnica permite una detección de bordes estable para tareas de segmentación de imágenes.
A partir de estas salidas, podemos calcular tanto la magnitud del gradiente como la dirección del gradiente (utilizando el operador arctangent) en cualquier píxel dado (x,y):
A partir de esto podemos determinar que los píxeles con grandes magnitudes son más propensos a ser un borde en la imagen, mientras que la dirección nos informa sobre la orientación del borde (aunque la dirección no es necesaria para generar nuestra salida).
Una implementación sencilla:
Aquí hay una implementación simple del operador Sobel en python (usando NumPy) para darle una idea del proceso (para todos los programadores en ciernes).
Esta implementación es una variante de python del ejemplo de pseudocódigo de Wikipedia, con el objetivo de mostrar cómo podría implementar este algoritmo, al tiempo que muestra los diversos pasos en el proceso.
¿Por qué nos importa?
Aunque la aproximación de gradiente producida por este operador es relativamente cruda, proporciona un método extremadamente eficiente computacionalmente para calcular bordes, esquinas y otras características geométricas de las imágenes. A su vez, ha allanado el camino para una serie de técnicas de reducción de dimensionalidad y extracción de características, como Patrones Binarios Locales (consulte mi otro blog para obtener más detalles sobre esta técnica).
Confiar en características exclusivamente geométricas corre el riesgo de perder información importante durante la codificación de nuestros datos, sin embargo, la compensación es lo que permite un procesamiento previo rápido de los datos y, a su vez, un entrenamiento rápido. Por lo tanto, esta técnica es especialmente útil en escenarios donde la textura y las características geométricas pueden considerarse muy importantes para definir la entrada. Esta es la razón por la que el reconocimiento facial se puede completar con un grado de precisión relativamente alto utilizando el operador Sobel. Sin embargo, esta técnica puede no ser la mejor opción si se trata de clasificar o agrupar entradas que utilizan el color como su principal factor diferenciador.
Este método sigue siendo extremadamente eficaz para obtener una representación de características geométricas de baja dimensión y un excelente punto de partida para la dimensionalidad y la reducción de ruido, antes de usar otros clasificadores o para su uso en metodologías de inferencia bayesianas.