Publicado en junio de 2008.
La segunda de dos columnas sobre las matemáticas de la topografía (la primera está aquí). …
Bill Casselman
Universidad de Columbia Británica, Vancouver, Canadá
cass at math.ubc.ca
John Eggers
Universidad de California, San Diego
jeggers en ucsd.edu
 Enviar un correo electrónico a un amigo Enviar un correo electrónico a un amigo |
 Imprimir este artículo Imprimir este artículo |
Un planímetro es un instrumento de mesa para medir áreas, generalmente las áreas de regiones irregulares en un mapa o fotografía. Antes eran comunes, pero ahora han sido reemplazadas en gran medida por herramientas digitales.
La siguiente imagen da una idea de la configuración. El brazo del poste gira libremente alrededor del poste, que se fija en la mesa. El brazo trazador gira alrededor del pivote, que es donde se une al brazo polar. Traza una curva en el sentido de las agujas del reloj con el trazador, y al hacerlo, la rueda de medición rueda y la distancia total que rueda se acumula en el dial. La rueda de soporte evita que la cosa se caiga. Al final, se lee un número del dial, y después de la multiplicación por un factor que depende solo de la configuración particular del planímetro, se obtiene el área dentro de la curva.

La siguiente figura da una mejor visión del mecanismo.

Llamamos al carro el conjunto de ruedas, dial y pivote. En la siguiente imagen, puede verlo mejor y ver la unidad de tornillo sin fin que hace que el dial gire a medida que se mueve la rueda de medición.

Aquí está el diagrama de la original planimeter, en el artículo de Jakob Amsler que introdujo:
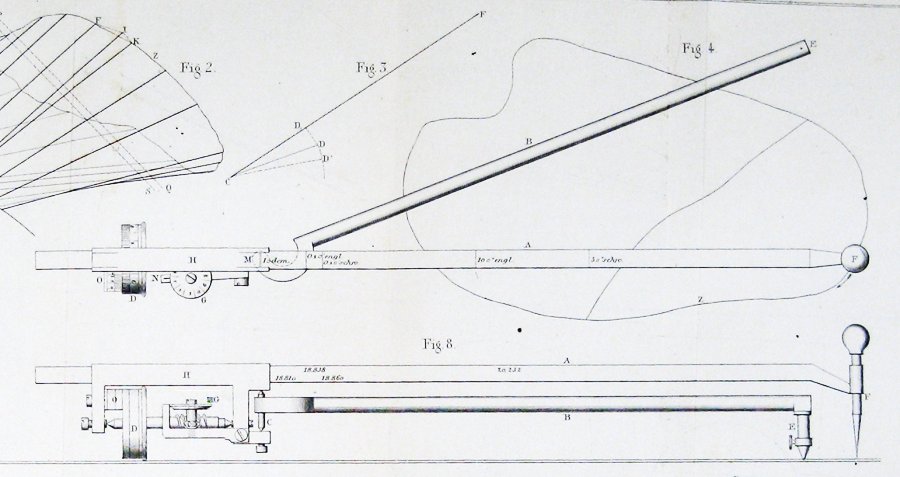
¿Cómo puede una cosa tan simple medir áreas?
Geometría del planímetro
El movimiento en el sentido de las agujas del reloj del planímetro es la dirección opuesta a lo que los matemáticos han decidido que debería ser la rotación positiva. En lugar de violar esta convención, vamos a trabajar a partir de ahora con un planímetro matemático, en el que se mueve en sentido contrario a las agujas del reloj. Al igual que las fantasías de otros matemáticos, ¡no hay ninguna en el planeta!
Hay algunas restricciones sobre cómo colocar el planímetro con respecto a la curva que desea trazar. El carro se puede deslizar a lo largo del brazo trazador, pero en todos los casos la longitud l del brazo trazador es menor que la longitud r del brazo del poste. Esto significa que el trazador nunca puede llegar a una distancia r-l del poste. Por otro lado, cuando está completamente extendido, el trazador nunca puede alcanzar más allá de r + l. Por lo tanto, la curva a trazar debe estar dentro del anillo entre dos círculos, uno con radio r – l y el otro r + l.

De hecho, debe quedar claro en un momento que los brazos nunca deben extenderse por completo, por lo que la curva a trazar debe estar completamente dentro del anillo. Además, normalmente el poste se coloca en el exterior de la curva.

Para un punto dado en el anillo hay exactamente dos configuraciones posibles del planímetro que colocan el trazador en ese punto. Elegir un punto u otro significa elegir un signo para una raíz cuadrada. A esto lo llamamos elegir una orientación para el planímetro. Es positivo si la raíz cuadrada es positiva. Una vez que se ha elegido una orientación, seguirá siendo la misma a menos que el brazo esté completamente extendido. Esto nunca debe suceder. Mientras su curva esté completamente dentro del anillo, las configuraciones del planímetro variarán sin problemas y de manera única con la trayectoria del trazador.
Lo siguiente que hay que hacer es comprender algunas cosas sobre el movimiento de la rueda de medición. Como se muestra en la siguiente imagen, si la rueda viaja en línea recta a distancia C, la rueda gira a través de un ángulo θ = C/R donde R es su radio.

Por lo que es realmente cierto que la rotación de la rueda y la distancia recorrida por el brazo trazador tienen alguna relación entre sí. Pero esta relación es un poco sutil. Si el brazo se mueve en línea recta una distancia C, el área barrida será lC, pero si se desplaza paralelo a sí mismo, el área barrida será 0. En el primer caso, un punto de la circunferencia de la rueda moverá la distancia C. En el segundo caso, la rueda no se moverá en absoluto. Y si el brazo se traduce oblicuamente, la rueda girará una distancia igual a la altitud del paralelogramo cubierto por el brazo. En todos los casos en que el brazo se traslade paralelo a sí mismo, el área barrida por la porción del brazo trazador entre el pivote y el trazador será igual a lC, donde C es la distancia medida por la rotación de la rueda. Este es el hecho básico que relaciona el movimiento del brazo con el movimiento de la rueda de medición.

La forma de expresar esto es precisamente que no importa cómo se mueva el brazo, la distancia medida por la rueda es la integral de la trayectoria

donde Γ es la trayectoria recorrida por el punto del brazo donde está unida la rueda de medición, n es el vector unitario perpendicular al brazo en cualquier momento, y t es el vector unitario que apunta en la dirección de viaje (de modo que, por ejemplo, si el brazo se mueve paralelo a sí mismo, el producto escalar de n y t es 0).
Teorema de Guldin
A continuación vamos a tratar de hacer que el comportamiento del planímetro sea intuitivamente claro, pero primero vamos a ver un tipo especial de planímetro, y en este caso probaremos un resultado más general. Supongamos que tomamos un solo brazo de longitud l que se mueve libremente y le colocamos una rueda de medición de radio R justo en su centro.

Luego movemos el brazo alrededor del plano. Si la rueda de medición gira a través de un ángulo total de θ radianes a medida que el brazo se mueve, la distancia que recorre un punto de la circunferencia es C = θR.
Teorema de Guldin. En esta situación, el área total barrida por el brazo es el producto lC.
el Área de aquí se interpreta con un signo. Si el brazo gira alrededor de su centro, una mitad del brazo va hacia adelante y la otra hacia atrás, y los dos se cancelan.
Ya hemos visto que la afirmación de Guldin es válida en el caso de que el brazo simplemente traduzca. Por supuesto, esto no siempre sucede: el brazo puede girar a medida que se mueve, así como traducirse. Pero podemos ver lo que está sucediendo cortando el área barrida de la siguiente manera:

Debido a que la rueda de medición está en el centro del brazo, a medida que el brazo gira, aplasta los pequeños bloques en un lado mientras los expande en el otro. Estos efectos se anulan entre sí exactamente.
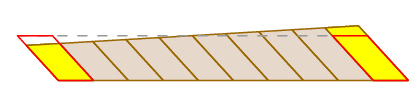
Se puede dar una prueba completamente rigurosa utilizando la fórmula para el cambio de variables en una integral doble y la expresión para el recorrido de la rueda como una integral de ruta.
Ahora supongamos que la rueda se coloca en otro lugar. Digamos que su posición es c + v donde c es el centro del brazo, y v un vector a lo largo del brazo. La longitud de v permanecerá fija, digamos en ρ. La trayectoria que sigue la rueda es c(t) + v (t). La integral de ruta es ahora
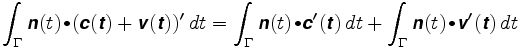
La primera integral es la distancia que recorrería la rueda si estuviera en el centro del brazo. En el segundo, el vector v(t) es siempre perpendicular a n, y v (t) tiene longitud constante. El vector v (t) se mueve alrededor de un círculo de radio igual a ρ. Por lo tanto, el producto escalar de n y v'(t) es solo la longitud con signo de v'(t), y la segunda integral es igual a ρ por la rotación total del brazo. Ahí:
Si la rueda está a una distancia ρ del centro del brazo, la distancia C que mide la rueda es C0, la distancia que se mediría si la rueda estuviera en el centro, más ρ veces el ángulo total θ en el que gira el brazo.
Puedes ver inmediatamente un caso simple de esto girando el brazo alrededor de su centro. Combinando esto con el teorema de Guldin, vemos que en todos los casos:
C = C0 + ρ θ
Área barrida = l C0 = l C – l ρ θ
El resultado completo
La fórmula de Guldin da un área con signo – si se barre hacia atrás sobre un área, la rueda va hacia atrás y se cancela el área que ya se ha cubierto. Si aplicamos esto al caso en el que el brazo libre vuelve exactamente a donde comenzó, vemos que lC es igual al área de la región cerrada trazada por el extremo derecho del brazo menos la de la región barrida por el izquierdo.
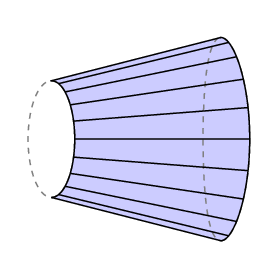
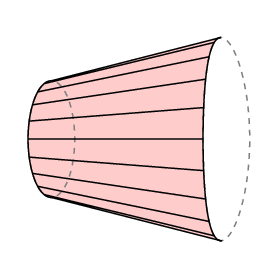

En el caso del planímetro polar, la parte inferior del brazo está restringida a un arco del círculo de radio r con centro en el polo, por lo tanto, l C es el área rastreado por el rastreador. Además, normalmente el polo se encuentra fuera de la región a medir, y en este caso la cantidad total de rotación del brazo tiene que ser 0. Así que en este caso tenemos
Área de la región trazada = lC
Aquí está la figura incluida por Jakob Amsler, el inventor, en su artículo original sobre el instrumento que inventó:
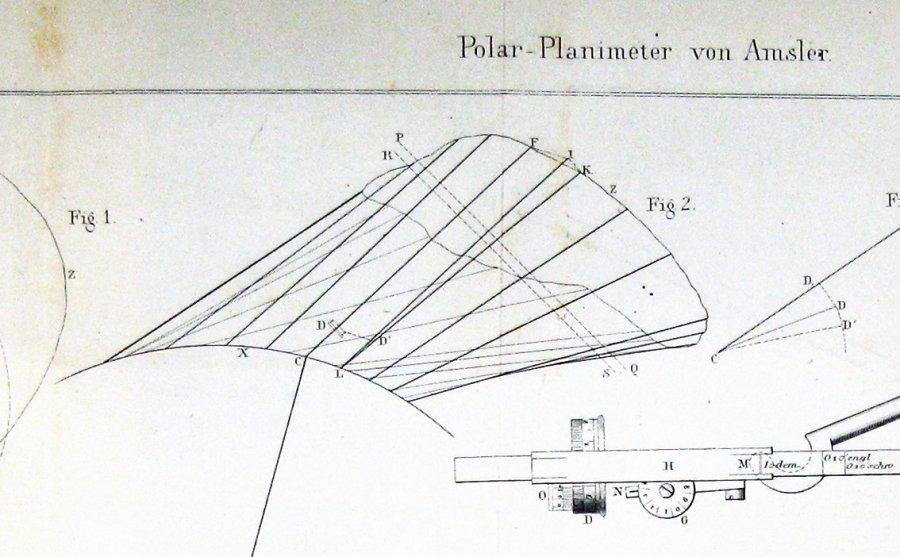
Parece bastante claro de esto que Amsler derivó su construcción a través de alguna forma del teorema de Guldin.
Planímetros y Teorema de Green
Como ya hemos mencionado, habiendo elegido la orientación del planímetro, la configuración del planímetro es una función continua de la posición del trazador. Digamos que elegimos la orientación positiva. Luego podemos unir a cada punto del anillo un vector unitario n, el que apunta en sentido contrario a las agujas del reloj y perpendicular al brazo trazador en el trazador.
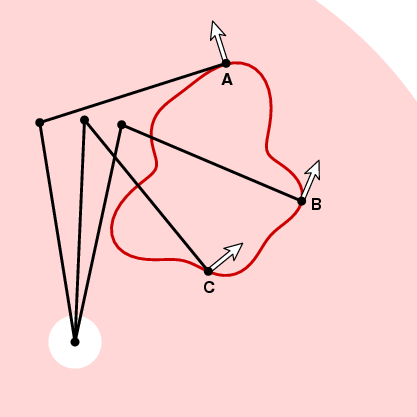
La forma en que la rueda de medición responderá al movimiento a lo largo de la curva en el siguiente instante depende del ángulo entre este vector y el vector tangente unitario de la curva. En A en la imagen de arriba, la rueda de medición no se va a mover porque el movimiento a lo largo de la curva es paralelo al brazo trazador. En B si el trazador se mueve una pequeña distancia ds, también lo hará la rueda de medición. Y en C, la rueda de medición se moverá a cierta distancia entre 0 y ds. Para ser precisos, supongamos que t es el vector tangente unitario en algún punto de la curva. Si el trazador mueve la distancia ds a lo largo de la curva, en ese punto la rueda de medición moverá una distancia d ds, donde d = n . t, el producto escalar de los vectores unitarios t y n. En otras palabras, si nos movemos alrededor de la curva Γ, la rueda de medición se moverá a una distancia total igual a la integral de n . t ds (producto escalar), o

Pero dado que cada punto del anillo corresponde a una configuración positiva única del planímetro, podemos asignar un vector n a cada punto interior del anillo, y por lo tanto define un campo vectorial. La curva Γ es el límite de su interior Ω, y por una de nuestras suposiciones esto está contenido enteramente en la región donde se define n. El teorema de Green nos dice que la integral de trayectoria alrededor del límite de esta región también es igual a una cierta integral sobre Ω: Por lo tanto,
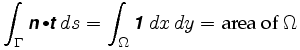
Más precisamente, el Verde del Teorema nos dicen que
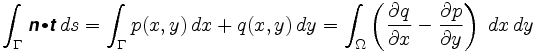
donde n = es el campo de vectores involucrados. El integrando en la integral doble se llama el rizo del campo vectorial.
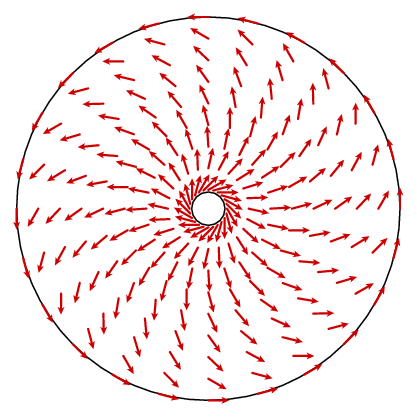
Esto no parece llevarnos muy lejos. Lo que debería suceder es que el rizo es una constante 1. En principio, podríamos encontrar una fórmula para el campo vectorial n y calcular su curvatura, pero eso no es muy esclarecedor. Sin embargo, podemos aprovechar otro hecho. El campo vectorial tiene simetría circular, lo que significa que está determinado por lo que es en un radio. La ley del coseno nos da una fórmula simple para el componente circunferencial.
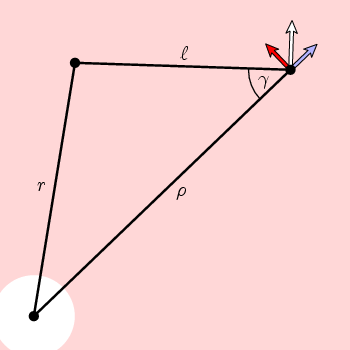
De la geometría simple de esta figura se desprende que el componente circunferencial de n es
f(ρ) = cos(γ) = (ρ 2 + l 2 – r 2)/(2 ρ l)
El punto real del teorema de Green es que para verificar que el integrando es 1 basta con verificar que la integral de la ruta alrededor de rutas pequeñas adecuadas es lo mismo que la zona. Para ello, elegimos nuestras regiones para que sean como aquí:
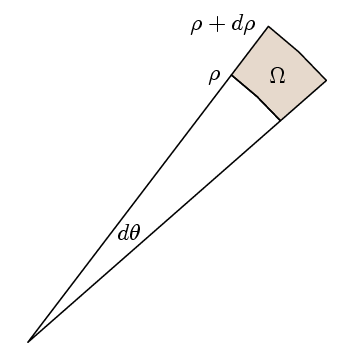
Entonces, l veces la ruta integral es
l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ
o
(θ/2) ( (ρ + dp) 2 – ρ 2)
que es el área de la región Ω.
Otros tipos de planímetros
El teorema de Guldin implica que el movimiento de una rueda de medición le dirá el área trazada por el trazador cada vez que el brazo con una rueda de medición en él traza una curva pero tiene un extremo restringido a una curva unidimensional. Esto sucede, por ejemplo, con el planímetro rodante, en el que el pivote se restringe a una línea recta al estar en un cilindro rodante.

Para saber más
-
 todavía hace y vende planimeters.
todavía hace y vende planimeters. - Cálculo diferencial e Integral Volumen II, R. Courant, Blackie & Son, 1936. La sección sobre la Fórmula de Guldin (pp.294-298) ofrece una explicación de cómo funciona el planímetro.
- Artículo original de Amsler, Vierteljahresschrift der Naturforschenden Gesellschaft en Zuerich, 1856. A esto le faltan los diagramas, pero están aquí:
- Primer diagrama de Amsler
- Segundo diagrama de Amsler
Nuestro agradecimiento a Donna Sammis de la Biblioteca de la Universidad de Stony Brook por localizar el artículo y a su esposo Robert por proporcionar fotografías de las figuras.
La compañía que fundó Amsler produjo instrumentos hasta bien entrado el siglo XX. Esta fotografía muestra el logotipo, en una versión de pantógrafo del planímetro:

- «Acerca de los planímetros», Suministro de ingeniería. La compañía también ha publicado un video en YouTube.
Bill Casselman
Universidad de Columbia Británica, Vancouver, Canadá
cass at math.ubc.ca
John Eggers
Universidad de California, San Diego
jeggers at ucsd.edu
Aquellos que pueden acceder a JSTOR pueden encontrar algunos de los documentos mencionados anteriormente allí. Para aquellos con acceso, el MathSciNet de la American Mathematical Society se puede usar para obtener información bibliográfica adicional y revisiones de algunos de estos materiales. Se puede acceder a algunos de los elementos anteriores a través del Portal ACM , que también proporciona servicios bibliográficos.