¿Qué es un modelo ARIMAX?

¿Cuál es el modelo ARIMAX?

Si ha leído nuestra serie de tutoriales de blog sobre modelos para estimar datos de series temporales, ya está familiarizado con 3 enfoques principales: autorregresión, medias móviles e integración.

¿Cuál es el tema común en todos estos modelos?

Solo dependían de una sola variable.

Sin embargo, un modelo también puede tener en cuenta algo más que los precios pasados o los residuos pasados.

Y estos son los llamados modelos «MAX», con el ARMAX siendo la versión no integrada y el ARIMAX-su equivalente integrado.

Así que, en este tutorial, vamos a explorar cómo se ven y le mostraremos cómo implementarlos en Python paso a paso.

Empecemos, ¿de acuerdo?

¿Por qué los modelos ARMAX y ARIMAX se llaman «MAX»?

Los nombres ARMAX y ARIMAX vienen como extensiones de ARMA y ARIMA respectivamente. La X añadida al final significa «exógeno». En otras palabras, sugiere agregar una variable externa diferente separada para ayudar a medir nuestra variable endógena.

La ecuación del modelo ARMAX y ARIMAX:

Dado que la única diferencia entre la ARMAX y la ARIMAX es que una está integrada y la otra no, podemos examinar una de ellas y luego resaltar cómo diferiría la otra.

Exploramos un modelo integrado en nuestro último artículo de blog (ARIMA), así que veamos cómo se ve la ecuación de ARIMAX.

ΔPt = c + ßX +11 ΔPt-1+θ1tt-1 +tt

Por supuesto, la ecuación para el ARMAX sería la misma, excepto que usaríamos la variable real, digamos P, en lugar de su delta.

Pt = c + ßX + Pt1 Pt-1 +θ1tt-1 + ht

Descomponiendo la ecuación de ARIMAX:

Podemos pensar en el ARMAX como un caso especial del ARIMAX, donde el orden de integración es 0.

Así que, para el resto del tutorial, nos centraremos en el ARIMAX.

Y comenzaremos por desglosar las diferentes partes en él. Para empezar, Pt y Pt-1 representan los valores en el período actual y 1 período atrás, respectivamente.

De manera similar, ϵt y ϵt-1 son los términos de error para los mismos dos períodos. Y, por supuesto, c es sólo un factor constante de referencia.

Los dos parámetros, θ1 y θ1, expresan qué partes del valor Pt-1 y el error ϵt-1 último período son relevantes para estimar el actual.

Ahora ,las dos nuevas adiciones al modelo son » X » y su coeficiente β. Al igual que ϕ, β es un coeficiente que se estimará en función de la selección del modelo y los datos. ¿Pero qué hay de X?

¿Qué es una variable exógena?

Bueno, X es la variable exógena y puede ser cualquier variable que nos interese.

Puede ser una medida que varía en el tiempo, como la tasa de inflación o el precio de un índice diferente. O una variable categórica que separa los diferentes días de la semana. También puede ser una contabilidad booleana para los períodos festivos especiales. Por último, puede representar una combinación de varios factores externos diferentes.

La idea es que puede ser cualquier otra variable o variables que puedan afectar a los precios, siempre y cuando tengamos los datos disponibles.

Estos factores externos se conocen como variables exógenas en nuestra regresión. Usamos sus valores para predecir y explicar el que nos interesa, que en nuestro caso son los precios actuales.

¿Cómo implementar modelos ARMAX y ARIMAX en Python?

Convenientemente, el paquete statsmodels viene con un método llamado ARIMA que es totalmente capaz de manejar tales entradas adicionales.

Comenzamos especificando las características del modelo y los pedidos del modelo:

Después de hacer esto, también necesitamos especificar el argumento exógeno llamado»exog».

El valor que queremos pasar debe ser una matriz de algún tipo, ya que queremos tener valores asociados con cada período de tiempo.

Por ejemplo, podemos usar S&precios P como esta variable exógena, ya que ya los tenemos en nuestros datos.

Ahora, estamos listos para montar un modelo ARIMAX (1,1,1).

Asegúrese de nombrar su variable de modelo de una manera que la distinga de modelos similares. En este caso, elegimos hacer esto agregando «X, spx» al final para indicar que la variable exógena es el S&P.

Luego, como se puede ver en los fragmentos, establecemos esto igual al método ARIMA como antes, agregamos la serie de tiempo y el orden, como estamos acostumbrados. Finalmente, entre los dos, establecemos el argumento » exog «igual a» DF SPX», que indica los precios S&P.

Si tenemos este modelo de ajuste de impresión y su tabla de resumen, vamos a ver que tenemos una fila adicional para el S&P precios.

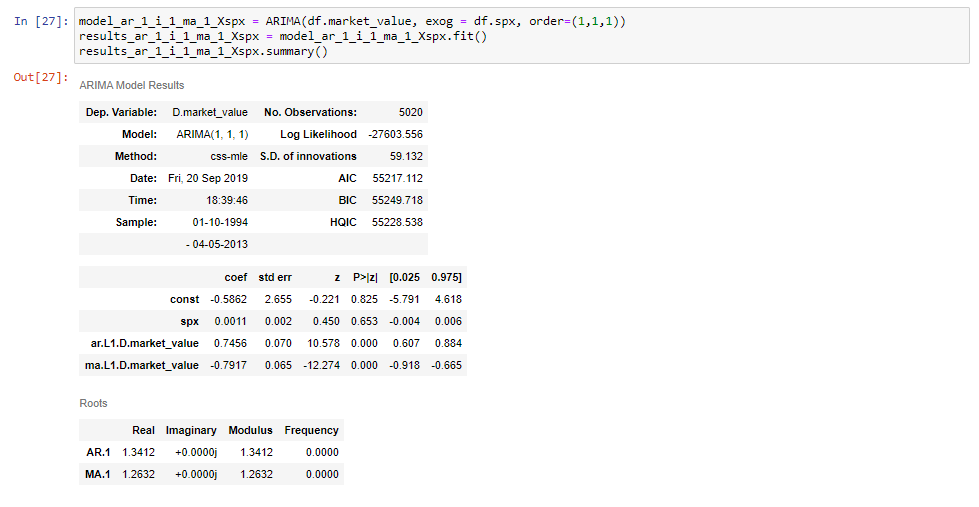
Y eso es todo lo que hay!

Hemos visto con éxito cómo implementar un modelo ARIMAX en Python.

Si desea obtener más información sobre ARIMAX y otros modelos de series temporales en Python, asegúrese de consultar nuestros tutoriales paso a paso de Python. Si es nuevo en Python y le entusiasma aprender más, este completo artículo sobre aprendizaje de programación en Python lo guiará desde la instalación, pasando por IDE, Bibliotecas y marcos de trabajo de Python, hasta las mejores trayectorias profesionales y perspectivas de trabajo de Python.

¿Listo para dar el siguiente paso hacia una carrera en ciencia de datos?

Echa un vistazo al Programa completo de Ciencia de Datos hoy mismo. Comience con los fundamentos con nuestros cursos de Estadísticas, Matemáticas y Excel. Desarrolle una experiencia paso a paso con SQL, Python, R, Power BI y Tableau. Y actualice su conjunto de habilidades con Aprendizaje Automático, Aprendizaje Profundo, Modelado de Riesgos de Crédito, Análisis de Series Temporales y Análisis de Clientes en Python. ¿Aún no estás seguro de que quieres convertir tu interés en la ciencia de datos en una carrera? Puede explorar el plan de estudios o inscribirse para 15 horas de contenido de video de principiante a avanzado de forma gratuita haciendo clic en el botón de abajo.