Introducción
El análisis de componentes principales (PCA) es un algoritmo de reducción de dimensionalidad que se puede usar para acelerar significativamente el algoritmo de aprendizaje de funciones sin supervisión. Lo que es más importante, comprender el PCA nos permitirá implementar más tarde el blanqueamiento, que es un paso importante de preprocesamiento para muchos algoritmos.
Supongamos que está entrenando su algoritmo con imágenes. Entonces la entrada será algo redundante, porque los valores de los píxeles adyacentes en una imagen están altamente correlacionados. En concreto, supongamos que estamos entrenando con parches de imagen en escala de grises de 16×16. Entonces \textstyle x \ in \ Re^{256} son 256 vectores dimensionales, con una característica \textstyle x_j correspondiente a la intensidad de cada píxel. Debido a la correlación entre píxeles adyacentes, el PCA nos permitirá aproximar la entrada con una dimensión mucho más baja, incurriendo en muy poco error.
Ejemplo y antecedentes matemáticos
Para nuestro ejemplo en ejecución, usaremos un conjunto de datos \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} con \textstyle n=2 entradas dimensionales, de modo que \textstyle x^{(i)} \in \Re^2. Supongamos que queremos reducir los datos de 2 dimensiones a 1. (En la práctica, es posible que queramos reducir los datos de 256 a 50 dimensiones, por ejemplo; pero el uso de datos de dimensiones inferiores en nuestro ejemplo nos permite visualizar mejor los algoritmos.) Aquí está nuestro conjunto de datos:
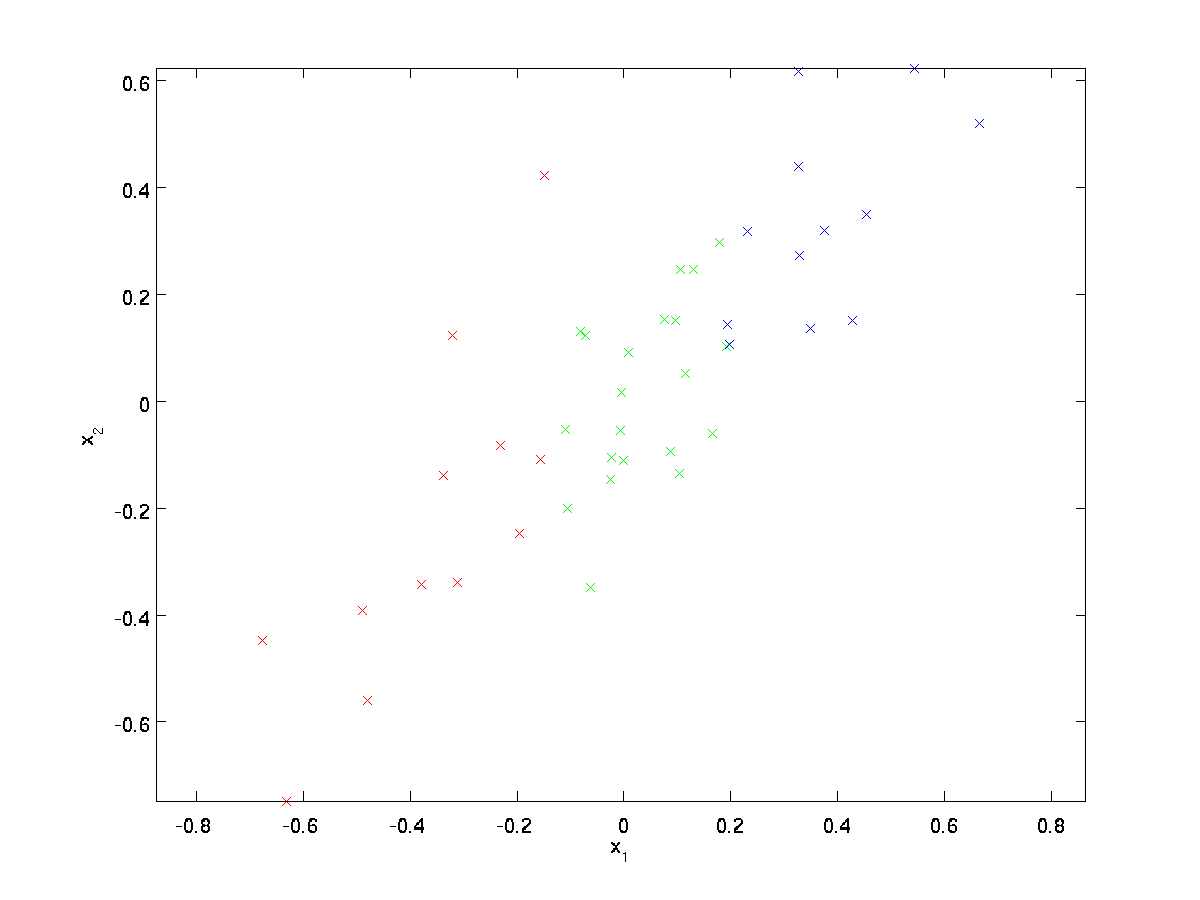
Estos datos ya se han procesado previamente para que cada una de las características \textstyle x_1 y \textstyle x_2 tengan aproximadamente la misma media (cero) y varianza.
A efectos de ilustración, también hemos coloreado cada uno de los puntos uno de los tres colores, dependiendo de su valor \textstyle x_1; estos colores no son utilizados por el algoritmo, y son solo para ilustración.
PCA encontrará un subespacio de dimensiones inferiores en el que proyectar nuestros datos.Al examinar visualmente los datos, parece que \textstyle u_1 es la dirección principal de variación de los datos, y \textstyle u_2 la dirección secundaria de variación:
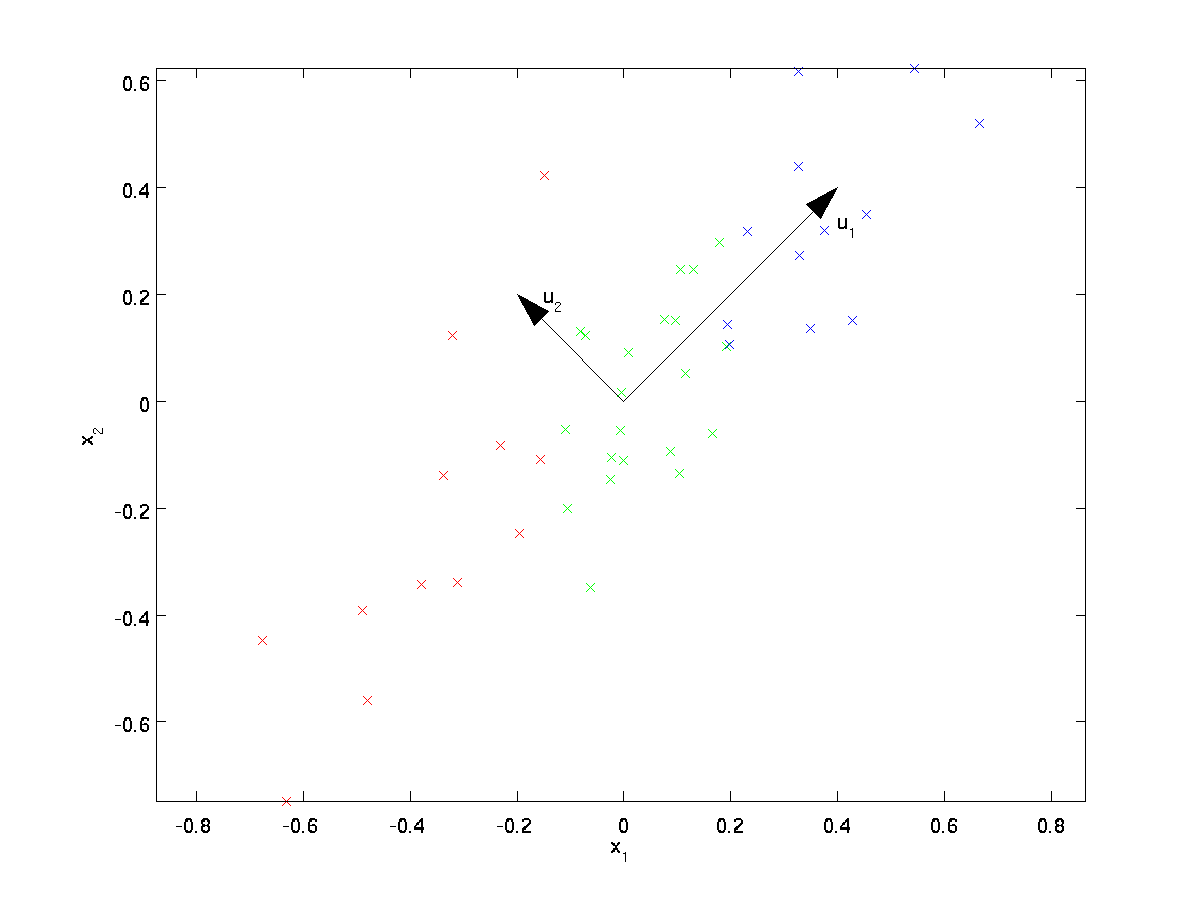
Es decir, los datos varían mucho más en la dirección \textstyle u_1 que en \textstyle u_2. Para encontrar de forma más formal las direcciones \textstyle u_1 y \textstyle u_2, primero calculamos la matriz \textstyle \ Sigma de la siguiente manera:
\ begin{align} \ Sigma=\frac{1}{m} \sum_{i = 1}^m (x^{(i)})(x^{(i)})^T. \end{align}
Si \textstyle x tiene media cero, entonces \textstyle \Sigma es exactamente la matriz de covarianza de \textstyle x. (El símbolo «\textstyle \Sigma», pronunciado «Sigma», es la notación estándar para denotar la matriz de covarianza. Desafortunadamente, se parece al símbolo de suma, como en \sum_{i = 1}^n i; pero estas son dos cosas diferentes.)
Se puede mostrar entonces que \textstyle u_1 – la dirección principal de variación de los datos-es el vector propio superior (principal) de \textstyle \Sigma, y \textstyle u_2 es el segundo vector propio.
Nota: Si está interesado en ver una derivación/justificación matemática más formal de este resultado, consulte las notas de la conferencia CS229 (Aprendizaje automático) sobre PCA (enlace al final de esta página). Sin embargo, no tendrá que hacerlo para seguir este curso.
Puede utilizar software de álgebra lineal numérica estándar para encontrar estos vectores propios (consulte las Notas de implementación). Concretamente, calculemos los vectores propios de \textstyle \ Sigma y apilemos los vectores propios en columnas para formar la matriz \textstyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
Los vectores \textstyle u_1 y \textstyle u_2 en nuestro ejemplo forman una nueva base en la que podemos representar los datos. Concretamente, deje que \textstyle x \ in \ Re^2 sea un ejemplo de entrenamiento. Entonces \textstyle u_1^Tx es la longitud (magnitud) de la proyección de \textstyle x sobre el vector \textstyle u_1.
De manera similar, \textstyle u_2^Tx es la magnitud de \textstyle x proyectada en el vector \textstyle u_2.
Girando los Datos
Así, podemos representar \textstyle x en la base \textstyle (u_1, u_2) calculando
\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}
(El subíndice «rot» proviene de la observación de que esto corresponde a una rotación (y posiblemente reflexión) del original data.) Tomemos todo el conjunto de entrenamiento y calculemos \textstyle x_ {\rm rot}^{(i)} = U^Tx^{(i)} para cada \textstyle i. Trazando estos datos transformados \textstyle x_{\rm rot}, obtenemos:

Este es el conjunto de entrenamiento girado en las bases \textstyle u_1,\textstyle u_2. En el caso general, \textstyle U^Tx será el conjunto de entrenamiento girado en la base \textstyle u_1,\textstyle u_2,…, \textstyle u_n.
Una de las propiedades de \textstyle U es que es una matriz «ortogonal», lo que significa que satisface \textstyle U^TU = UU^T = I. Por lo tanto, si alguna vez necesita pasar de los vectores girados \textstyle x_{\rm rot} a los datos originales \textstyle x, puede calcular
\begin{align}x = U x_{\rm rot}, \end{align}
porque \textstyle U x_{\rm rot} = UU^T x = x.
Reduciendo la dimensión de datos
Vemos que la dirección principal de variación de los datos es la primera dimensión \textstyle x_{\rm rot, 1} de estos datos girados. Por lo tanto, si queremos reducir los datos a una dimensión, podemos establecer
\begin{align}\tilde{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} \in \Re.\end{align}
Más generalmente, si \textstyle x \ in \ Re^n y queremos reducirlo a una representación dimensional \textstyle k \textstyle \ tilde{x} \ in \Re^k (donde k < n), tomaremos los primeros componentes \textstyle k de \textstyle x_{\rm rot}, que corresponden a las direcciones de variación \textstyle k superiores.
Otra forma de explicar el PCA es que \textstyle x_ {\rm rot} es un vector dimensional \textstyle n, donde es probable que los primeros componentes sean grandes (p. ej., en nuestro ejemplo, vimos que \textstyle x_ {\rm rot, 1}^{(i)} = u_1^Tx^{(i)} toma valores razonablemente grandes para la mayoría de los ejemplos \textstyle i), y es probable que los componentes posteriores sean pequeños (por ejemplo, en nuestro ejemplo, \textstyle x_{\rm rot, 2}^{(i)} = u_2^Tx^{(i)} era más probable que fueran pequeños). Lo que hace PCA es eliminar los componentes posteriores (más pequeños) de \textstyle x_{\rm rot}, y simplemente aproximarlos con 0. Concretamente, también se puede llegar a nuestra definición de \textstyle \tilde{x} utilizando una aproximación a \textstyle x_{\rm rot} donde todos los componentes de \textstyle k, excepto los primeros, son ceros. En otras palabras, tenemos:
\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\approx \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,k+1} \\\vdots \\ x_{\rm rot,n} \end{bmatrix}= x_{\rm rot} \end{alinean}
En nuestro ejemplo, esto nos da la siguiente parcela de \estilo de texto \tilde{x} (utilizando \estilo de texto n=2, k=1):

Sin embargo, dado que los componentes finales \textstyle n-k de \textstyle \tilde{x} como se define anteriormente siempre serían cero, no es necesario mantener estos ceros alrededor, por lo que definimos \textstyle \tilde{x} como un vector \textstyle k-dimensional con solo los primeros componentes \textstyle k (distintos de cero).
Esto también explica por qué queríamos expresar nuestros datos en la base \textstyle u_1, u_2, \ldots, u_n: Decidir qué componentes conservar se convierte simplemente en mantener los componentes \textstyle k superiores. Cuando hacemos esto, también decimos que estamos «conservando los componentes top \textstyle k PCA (o principales).»
Recuperar una aproximación de los Datos
Ahora, \textstyle \ tilde{x} \ in \ Re^k es una representación «comprimida» de dimensiones inferiores del \textstyle x \in \Re^n. Dado \textstyle \tilde{x}, ¿cómo podemos recuperar una aproximación \textstyle \hat{x} al valor original de \textstyle x? De una sección anterior, sabemos que \textstyle x = U x_ {\rm rot}. Además, podemos pensar en \textstyle \ tilde{x} como una aproximación a \textstyle x_ {\rm rot}, donde hemos establecido los últimos componentes \textstyle n-k en ceros. Por lo tanto, dado \estilo de texto \tilde{x} \in \Re^k, podemos rellenar con \estilo de texto n-k ceros para obtener nuestra aproximación a \estilo de texto x_{\rm rot} \in \Re^n. Finalmente, se pre-multiplicar por \estilo de texto U obtener nuestra aproximación a \estilo de texto x. Concretamente, obtenemos
\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}
La igualdad final anterior proviene de la definición de \textstyle U dada anteriormente. (En una implementación práctica, en realidad no tendríamos cero pad \textstyle \ tilde{x} y luego multiplicaríamos por \textstyle U, ya que eso significaría multiplicar muchas cosas por ceros; en su lugar, simplemente multiplicaríamos \textstyle \tilde{x} \in \Re^k con las primeras columnas \textstyle k de \textstyle U como en la expresión final anterior.) Aplicando esto a nuestro conjunto de datos, obtenemos la siguiente gráfica para \textstyle \ hat{x}:
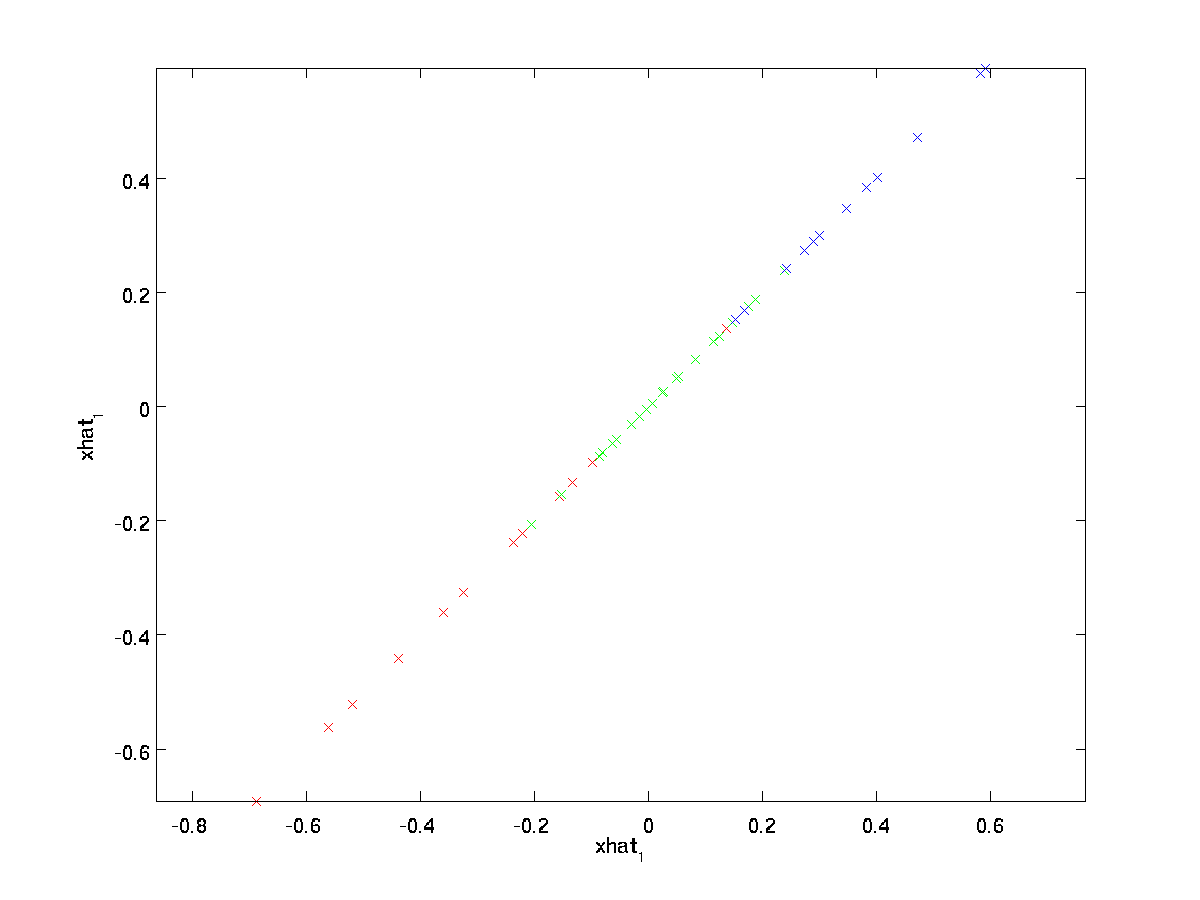
Por lo tanto, estamos utilizando una aproximación de 1 dimensión al conjunto de datos original.
Si está entrenando un autocodificador u otro algoritmo de aprendizaje de funciones no supervisado, el tiempo de ejecución de su algoritmo dependerá de la dimensión de la entrada. Si introduce \textstyle \tilde{x} \in \Re^k en su algoritmo de aprendizaje en lugar de \textstyle x, entonces estará entrenando en una entrada de menor dimensión, y por lo tanto su algoritmo podría ejecutarse significativamente más rápido. Para muchos conjuntos de datos, la representación de dimensiones inferiores \textstyle \tilde{x} puede ser una aproximación extremadamente buena al original, y usar PCA de esta manera puede acelerar significativamente su algoritmo al tiempo que introduce muy poco error de aproximación.
Número de componentes a conservar
¿Cómo establecemos \textstyle k; es decir, cuántos componentes de PCA debemos conservar? En nuestro ejemplo simple de 2 dimensiones, parecía natural retener 1 de los 2 componentes, pero para datos de dimensiones más altas, esta decisión es menos trivial. Si \textstyle k es demasiado grande, no comprimiremos mucho los datos; en el límite de \textstyle k=n, solo usaremos los datos originales (pero girados en una base diferente). Por el contrario, si \textstyle k es demasiado pequeño, entonces podríamos estar usando una muy mala aproximación a los datos.
Para decidir cómo establecer \textstyle k, normalmente veremos el «‘porcentaje de varianza retenido «‘ para diferentes valores de \textstyle k. Concretamente, si \textstyle k = n, entonces tenemos una aproximación exacta a los datos, y decimos que se retiene el 100% de la varianza. I. e., toda la variación de los datos originales se conserva. Por el contrario, si \textstyle k = 0, entonces estamos aproximando todos los datos con el vector cero, y por lo tanto se retiene el 0% de la varianza.
De forma más general, deje que \textstyle \ lambda_1, \lambda_2, \ldots, \lambda_n sean los valores propios de \textstyle \ Sigma (ordenados en orden decreciente), de modo que \textstyle \lambda_j sea el valor propio correspondiente al vector propio \textstyle u_j. Entonces, si conservamos los componentes principales de \textstyle k, el porcentaje de varianza retenido viene dado por:
\ begin{align}\frac {\sum_{j = 1}^k \lambda_j} {\sum_{j=1}^n \lambda_j}.\end{align}
En nuestro ejemplo 2D simple anterior, \textstyle \lambda_1 = 7.29, y \textstyle \lambda_2 = 0.69. Por lo tanto, al mantener solo los componentes principales de \textstyle k=1, conservamos \textstyle 7.29/(7.29+0.69) = 0.913, o el 91,3% de la varianza.
Una definición más formal del porcentaje de varianza retenido está fuera del alcance de estas notas. Sin embargo,es posible mostrar que \textstyle \lambda_j =\sum_{i=1}^m x_{\rm rot, j}^2. Por lo tanto, si \textstyle \lambda_j \approx 0,muestra que \textstyle x_{\rm rot, j} suele estar cerca de 0 de todos modos, y perdemos relativamente poco al aproximarlo con una constante 0. Esto también explica por qué conservamos los componentes principales superiores (correspondientes a los valores más grandes de \textstyle \lambda_j) en lugar de los inferiores. Los componentes principales superiores \textstyle x_{\rm rot,j} son los que son más variables y que toman valores más grandes, y para los que incurriríamos en un error de aproximación mayor si los pusiéramos a cero.
En el caso de las imágenes, una heurística común es elegir \textstyle k para retener el 99% de la varianza. En otras palabras, elegimos el valor más pequeño de \textstyle k que satisface
\ begin{align}\frac {\sum_{j = 1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}
Dependiendo de la aplicación, si está dispuesto a incurrir en algún error adicional, a veces también se usan valores en el rango del 90-98%. Cuando describes a otros cómo aplicaste PCA, decir que elegiste \textstyle k para retener el 95% de la varianza también será una descripción mucho más fácil de interpretar que decir que conservaste 120 (o cualquier otro número de) componentes.
PCA en imágenes
Para que el PCA funcione, normalmente queremos que cada una de las características \textstyle x_1, x_2, \ldots, x_n tenga un rango de valores similar al de las demás (y una media cercana a cero). Si ha utilizado PCA en otras aplicaciones anteriormente, es posible que haya preprocesado por separado cada característica para tener cero media y varianza unitaria, estimando por separado la media y la varianza de cada característica \textstyle x_j. Sin embargo, este no es el preprocesamiento que aplicaremos a la mayoría de los tipos de imágenes. En concreto, supongamos que estamos entrenando nuestro algoritmo en «‘imágenes naturales»‘, de modo que \textstyle x_j es el valor de pixel \textstyle j. Por» imágenes naturales», nos referimos informalmente al tipo de imagen que un animal o persona típico podría ver a lo largo de su vida.
Nota: Por lo general, utilizamos imágenes de escenas al aire libre con césped, árboles, etc., y recorta pequeños parches de imagen (digamos 16×16) aleatoriamente de estos para entrenar el algoritmo. Pero en la práctica, la mayoría de los algoritmos de aprendizaje de funciones son extremadamente robustos para el tipo exacto de imagen en el que se entrena, por lo que la mayoría de las imágenes tomadas con una cámara normal, siempre que no sean excesivamente borrosas o tengan artefactos extraños, deberían funcionar.
Al entrenar con imágenes naturales, tiene poco sentido estimar una media y varianza separadas para cada píxel, porque las estadísticas en una parte de la imagen deberían (teóricamente) ser las mismas que cualquier otra.
Esta propiedad de las imágenes es llamado «‘estacionariedad.»‘
En detalle, para que el PCA funcione bien, informalmente requerimos que (i) Las características tengan una media aproximadamente cero, y (ii) Las diferentes características tengan variaciones similares entre sí. Con imágenes naturales, (ii) ya está satisfecho incluso sin normalización de varianza, por lo que no realizaremos ninguna normalización de varianza.
(Si está entrenando en datos de audio, por ejemplo, en espectrogramas, o en datos de texto, por ejemplo, vectores de bolsa de palabras, generalmente tampoco realizaremos normalización de varianza.De hecho, PCA es invariante a la escala de los datos, y devolverá los mismos vectores propios independientemente de la escala de la entrada. Más formalmente, si multiplica cada vector de entidad \ textstyle x por algún número positivo (escalando así cada entidad en cada ejemplo de entrenamiento por el mismo número), los vectores propios de salida de PCA no cambiarán.
Por lo tanto, no usaremos normalización de varianza. La única normalización que necesitamos realizar entonces es la normalización de medias, para asegurarnos de que las características tengan una media alrededor de cero. Dependiendo de la aplicación, muy a menudo no estamos interesados en cuán brillante es la imagen de entrada general. Por ejemplo, en las tareas de reconocimiento de objetos, el brillo general de la imagen no afecta a los objetos que hay en la imagen. Más formalmente, no estamos interesados en el valor de intensidad media de un parche de imagen; por lo tanto, podemos restar este valor, como una forma de normalización media.
Concretamente, si \textstyle x^{(i)} \in \Re^{n} son los valores de intensidad (en escala de grises) de un parche de imagen de 16×16 (\textstyle n=256), podríamos normalizar la intensidad de cada imagen \textstyle x^{(i)} de la siguiente manera:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}
para todos los \textstyle j
Tenga en cuenta que los dos pasos anteriores se realizan por separado para cada imagen \textstyle x^{(i)}, y que \textstyle \mu^{(i)} aquí está la intensidad media de la imagen \textstyle x^{(i)}. En particular, esto no es lo mismo que estimar un valor medio por separado para cada píxel \textstyle x_j.
Si está entrenando su algoritmo en imágenes que no sean imágenes naturales (por ejemplo, imágenes de caracteres escritos a mano o imágenes de objetos aislados centrados sobre un fondo blanco), vale la pena considerar otros tipos de normalización, y la mejor opción puede depender de la aplicación. Pero al entrenar con imágenes naturales, usar el método de normalización media por imagen como se indica en las ecuaciones anteriores sería un valor predeterminado razonable.
Blanqueamiento
Hemos utilizado PCA para reducir la dimensión de los datos. Hay un paso de preprocesamiento estrechamente relacionado llamado blanqueamiento (o, en algunas otras literaturas, esférico) que se necesita para algunos algoritmos. Si estamos entrenando en imágenes, la entrada en bruto es redundante, ya que los valores de píxeles adyacentes están altamente correlacionados. El objetivo del blanqueamiento es hacer que la entrada sea menos redundante; más formalmente, nuestros deseos son que nuestros algoritmos de aprendizaje vean una entrada de entrenamiento donde (i) las características están menos correlacionadas entre sí, y (ii) todas las características tienen la misma varianza.
Ejemplo 2D
Primero describiremos el blanqueamiento utilizando nuestro ejemplo 2D anterior. Luego describiremos cómo se puede combinar esto con suavizado y, finalmente, cómo combinarlo con PCA.
¿Cómo podemos hacer que nuestras funciones de entrada no estén correlacionadas entre sí? Ya habíamos hecho esto al calcular \textstyle x_ {\rm rot}^{(i)} = U^Tx^{(i)}.
Repetir nuestra figura anterior, nuestra parcela para \estilo de texto x_{\rm rot} fue:

La matriz de covarianza de los datos está dada por:
\begin{align}\begin{bmatrix}7.29 && 0.69\end{bmatrix}.\end{align}
(Nota: Técnicamente, muchas de las afirmaciones de esta sección sobre la «covarianza» solo serán verdaderas si los datos tienen media cero. En el resto de esta sección, tomaremos esta suposición como implícita en nuestras declaraciones. Sin embargo, incluso si la media de los datos no es exactamente cero, las intuiciones que presentamos aquí siguen siendo ciertas, por lo que esto no es algo de lo que deba preocuparse.)
No es casualidad que los valores diagonales sean \textstyle \ lambda_1 y \textstyle \ lambda_2. Además, las entradas fuera de diagonal son cero; por lo tanto, \textstyle x_{\rm rot,1} y \textstyle x_{\rm rot, 2} no están correlacionados, satisfaciendo uno de nuestros desideratos para datos blanqueados (que las características estén menos correlacionadas).
Para que cada una de nuestras características de entrada tenga varianza de unidad, simplemente podemos volver a escalar cada característica \textstyle x_{\rm rot,i} por \textstyle 1/\sqrt{\lambda_i}. Concretamente, definimos nuestros datos blanqueados \textstyle x_ {\rm PCAwhite} \ in \ Re^n de la siguiente manera:
\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \end{align}
Trazado \ textstyle x_ {\rm PCAwhite}, obtenemos:

Estos datos ahora tienen covarianza igual a la matriz de identidad \textstyle I. Decimos que \textstyle x_{\rm PCAwhite} es nuestra versión blanqueada de PCA de los datos: Los diferentes componentes de \textstyle x_{\rm PCAwhite} no están correlacionados y tienen varianza de unidad.
Blanqueamiento combinado con reducción de dimensionalidad. Si desea tener datos blanqueados y de dimensiones inferiores a la entrada original, también puede conservar opcionalmente solo los componentes superiores \textstyle k de \textstyle x_{\rm PCAwhite}. Cuando combinamos el blanqueamiento de PCA con la regularización (descrito más adelante), los últimos componentes de \textstyle x_{\rm PCAwhite} serán casi cero de todos modos, y por lo tanto se pueden eliminar de forma segura.
Blanqueamiento ZCA
Finalmente, resulta que esta forma de conseguir que los datos tengan covarianza identity \textstyle I no es única. Concretamente, si \textstyle R es cualquier matriz ortogonal, de modo que satisfaga \textstyle RR^T = R^TR = I (de forma menos formal, si \textstyle R es una matriz de rotación/reflexión), entonces \textstyle R \,x_{\rm PCAwhite} también tendrá covarianza de identidad.
En el blanqueamiento ZCA, elegimos \textstyle R = U. Definimos
\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}
Trazado \textstyle x_{\rm ZCAwhite}, obtenemos:

Se puede mostrar que fuera de todas las opciones posibles para \textstyle R, esta elección de rotación hace que \textstyle x_{\rm ZCAwhite} se acerque lo más posible a los datos de entrada originales \textstyle x.
Cuando se usa blanqueamiento ZCA (a diferencia del blanqueamiento PCA), generalmente conservamos todas las dimensiones \textstyle n de los datos, y no intentamos reducir su dimensión.
Regularización
Al implementar blanqueamiento PCA o blanqueamiento ZCA en la práctica, a veces algunos de los valores propios \textstyle \ lambda_i serán numéricamente cercanos a 0, y por lo tanto el paso de escalado donde dividimos por \sqrt{\lambda_i} implicaría dividir por un valor cercano a cero; esto puede hacer que los datos exploten (tomen valores grandes) o sean numéricamente inestables. En la práctica, por lo tanto, implementamos este paso de escalado utilizando una pequeña cantidad de regularización, y agregamos una pequeña constante \textstyle \epsilon a los valores propios antes de tomar su raíz cuadrada e inversa:
\ begin{align}x_ {\rm PCAwhite, i} = \frac{x_ {\rm rot, i} }{\sqrt {\lambda_i + \epsilon}}.\end{align}
Cuando \textstyle x toma valores alrededor de \textstyle, puede ser típico un valor de \textstyle \epsilon \approx 10^{-5}.
Para el caso de las imágenes, agregar \textstyle \epsilon aquí también tiene el efecto de suavizar ligeramente (o filtrar paso bajo) la imagen de entrada. Esto también tiene el efecto deseable de eliminar los artefactos de aliasing causados por la forma en que se presentan los píxeles en una imagen, y puede mejorar las características aprendidas (los detalles están más allá del alcance de estas notas).
El blanqueamiento ZCA es una forma de procesamiento previo de los datos que lo mapea de \textstyle x a \textstyle x_ {\rm ZCAwhite}. Resulta que este es también un modelo aproximado de cómo el ojo biológico (la retina) procesa las imágenes. Específicamente, a medida que su ojo percibe imágenes, la mayoría de los «píxeles» adyacentes en su ojo percibirán valores muy similares, ya que las partes adyacentes de una imagen tienden a estar altamente correlacionadas en intensidad. Por lo tanto, es un desperdicio para su ojo tener que transmitir cada píxel por separado (a través de su nervio óptico) a su cerebro. En su lugar, su retina realiza una operación de descorrelación (esto se realiza a través de neuronas retinianas que calculan una función llamada «en el centro, off surround/off center, on surround») que es similar a la realizada por ZCA. Esto da como resultado una representación menos redundante de la imagen de entrada, que luego se transmite al cerebro.
Implementación de blanqueamiento PCA
En esta sección, resumimos los algoritmos de blanqueamiento PCA, blanqueamiento PCA y blanqueamiento ZCA, y también describimos cómo puede implementarlos utilizando bibliotecas de álgebra lineal eficientes.
En primer lugar, debemos asegurarnos de que los datos tengan (aproximadamente) media cero. Para imágenes naturales, logramos esto (aproximadamente) restando el valor medio de cada parche de imagen.
Logramos esto calculando la media para cada parche y restándola para cada parche. En Matlab, podemos hacer esto usando
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);A continuación, necesitamos calcular \textstyle \ Sigma = \ frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. Si está implementando esto en Matlab (o incluso si está implementando esto en C++, Java, etc., pero tener acceso a una biblioteca de álgebra lineal eficiente), hacerlo como una suma explícita es ineficiente. En su lugar, podemos calcular esto de un solo golpe como
sigma = x * x' / size(x, 2);(Verifique la corrección de las matemáticas usted mismo.) Aquí, asumimos que x es una estructura de datos que contiene un ejemplo de entrenamiento por columna (por lo tanto, x es una matriz \textstyle n por\textstyle m).
A continuación, PCA calcula los vectores propios de \Sigma. Se podría hacer esto utilizando la función Matlab eig. Sin embargo, debido a que \Sigma es una matriz semidefinida positiva simétrica, es más confiable numéricamente hacer esto usando la función svd. Concretamente, si implementa
= svd(sigma);entonces la matriz U contendrá los vectores propios de \Sigma (un vector propio por columna, ordenado en orden de arriba a abajo), y las entradas diagonales de la matriz S contendrán los valores propios correspondientes (también ordenados en orden decreciente). La matriz V será igual a U, y puede ser ignorada con seguridad.
(Nota: La función svd realmente calcula los vectores singulares y los valores singulares de una matriz, que para el caso especial de una matriz semidefinida positiva simétrica, que es todo lo que nos preocupa aquí, es igual a sus vectores propios y valores propios. Una discusión completa de vectores singulares vs. vectores propios está más allá del alcance de estas notas.)
Finalmente, puede calcular \textstyle x_ {\rm rot} y \textstyle \ tilde{x} de la siguiente manera:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepEsto le da a su PCA una representación de los datos en términos de \textstyle \tilde{x} \in \Re^k. Por cierto, si x es una matriz \textstyle n por\textstyle m que contiene todos los datos de entrenamiento, esta es una implementación vectorizada, y las expresiones anteriores también funcionan para calcular x_{\rm rot} y \tilde{x} para todo el conjunto de entrenamiento de una sola vez. El resultado x_ {\rm rot} y \ tilde{x} tendrán una columna correspondiente a cada ejemplo de entrenamiento.
Para calcular los datos blanqueados de PCA \textstyle x_{\rm PCAwhite}, use
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;Dado que la diagonal de S contiene los valores propios \textstyle \lambda_i, esta resulta ser una forma compacta de calcular \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}} simultáneamente para todos los \textstyle i.
Finalmente, también puede calcular los datos blanqueados de ZCA \textstyle x_{\rm ZCAwhite} como:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;