En el artículo de hoy, vamos a echar un vistazo a las ventanas enrollables y ampliables.
Al final de la publicación, podrá responder a estas preguntas:
- ¿Qué es una ventana móvil?
- ¿Qué es una ventana en expansión?
- ¿por Qué son útiles?
¿Qué es una ventana móvil o en expansión?

Aquí es una ventana normal.
Usamos ventanas normales porque queremos echar un vistazo al exterior, cuanto más grande es la ventana, más del exterior podemos ver.
También como regla general, cuanto más grandes sean las ventanas de la casa de alguien, mejor será su cartera de acciones
Al igual que las ventanas reales, las ventanas de datos también nos ofrecen un pequeño vistazo a algo más grande.
Una ventana móvil nos permite investigar un subconjunto de nuestros datos.
Ventanas móviles
Muchas veces, queremos conocer una propiedad estadística de nuestros datos de series temporales, pero debido a que todas las máquinas del tiempo están bloqueadas en Roswell, no podemos calcular una estadística sobre la muestra completa y usarla para obtener información.
Eso introduciría un sesgo de anticipación en nuestra investigación.
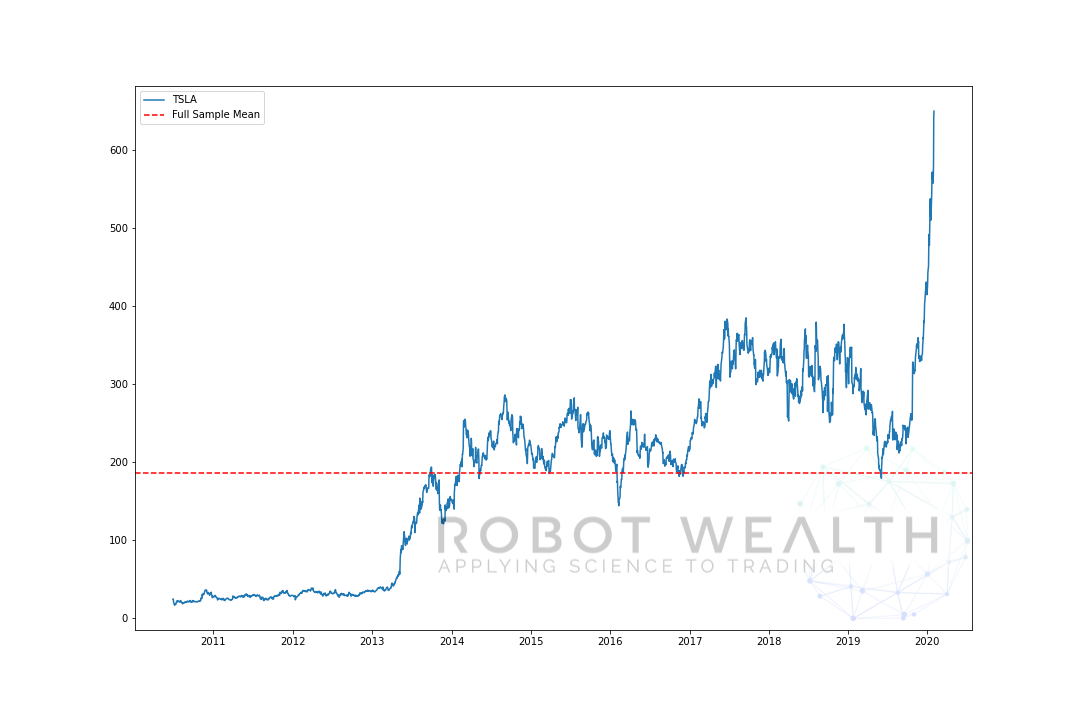
Aquí hay un ejemplo extremo de eso. Aquí hemos trazado el precio de TSLA y su media sobre la muestra completa.
import pandas as pdimport matplotlib.pyplot as plt #Load TSLA OHLC df = pd.read_csv('TSLA.csv')#Calculate full sample meanfull_sample_mean = df.mean()#Plotplt.plot(df,label='TSLA')plt.axhline(full_sample_mean,linestyle='--',color='red',label='Full Sample Mean')plt.legend()plt.show()
En este caso, si acabamos de comprar TSLA cuando el precio estaba por debajo de la media y lo vendemos por encima de la media, habríamos hecho una matanza, bueno, al menos hasta 2019
Pero el problema es que no habríamos conocido el valor medio en ese momento.
Así que es bastante obvio por qué no podemos usar toda la muestra, pero ¿qué podemos hacer entonces? Una forma de abordar este problema es mediante el uso de ventanas enrollables o expandibles.
Si alguna vez has utilizado una Media Móvil Simple, felicitaciones, has utilizado una ventana móvil.
¿Cómo funcionan las ventanas enrollables?
Supongamos que tiene 20 días de datos de existencias y desea conocer el precio medio de las existencias de los últimos 5 días. ¿Qué es lo que haces?
tome los últimos 5 días, sumarlos y dividir por 5.
Pero, ¿qué pasa si desea conocer el promedio de los 5 días anteriores para cada día en su conjunto de datos?
Aquí es donde rolling windows puede ayudar.
En este caso, nuestra ventana tendría un tamaño de 5, lo que significa que para cada punto en el tiempo contiene la media de los últimos 5 puntos de datos.
Visualicemos un ejemplo con una ventana móvil de tamaño 5 paso a paso.
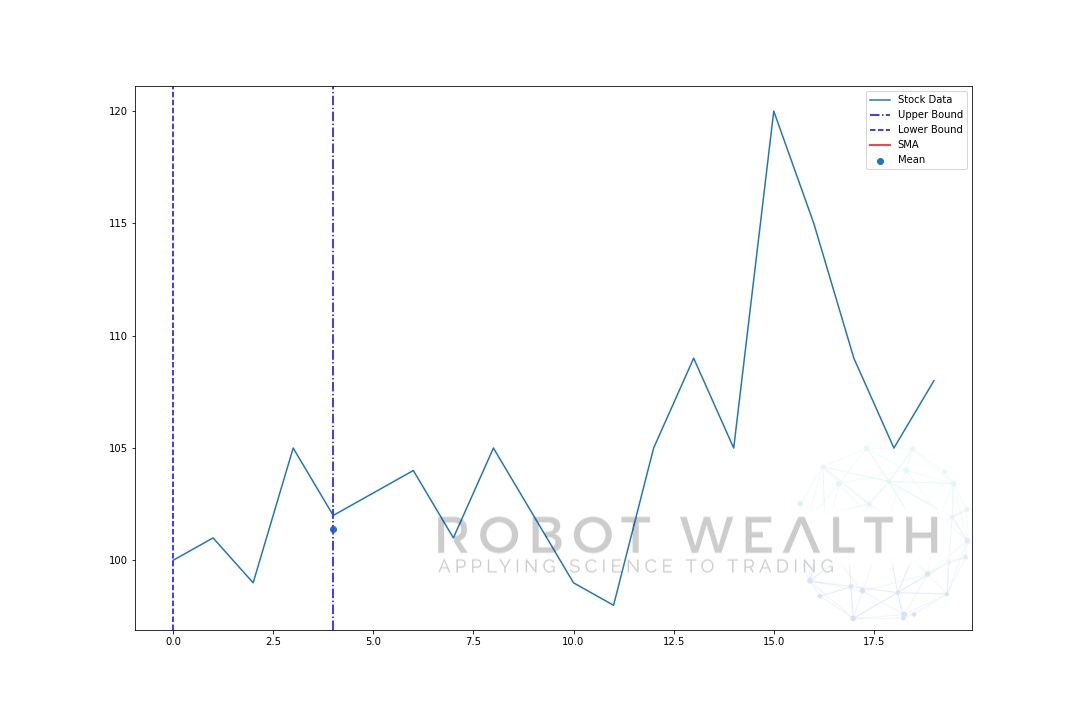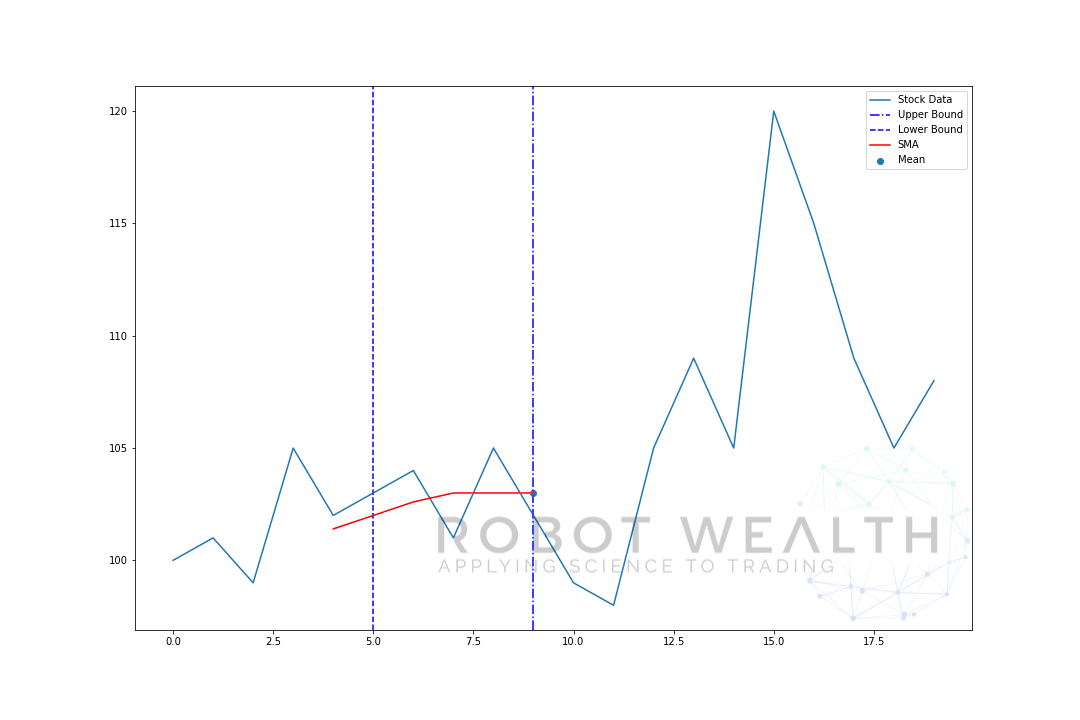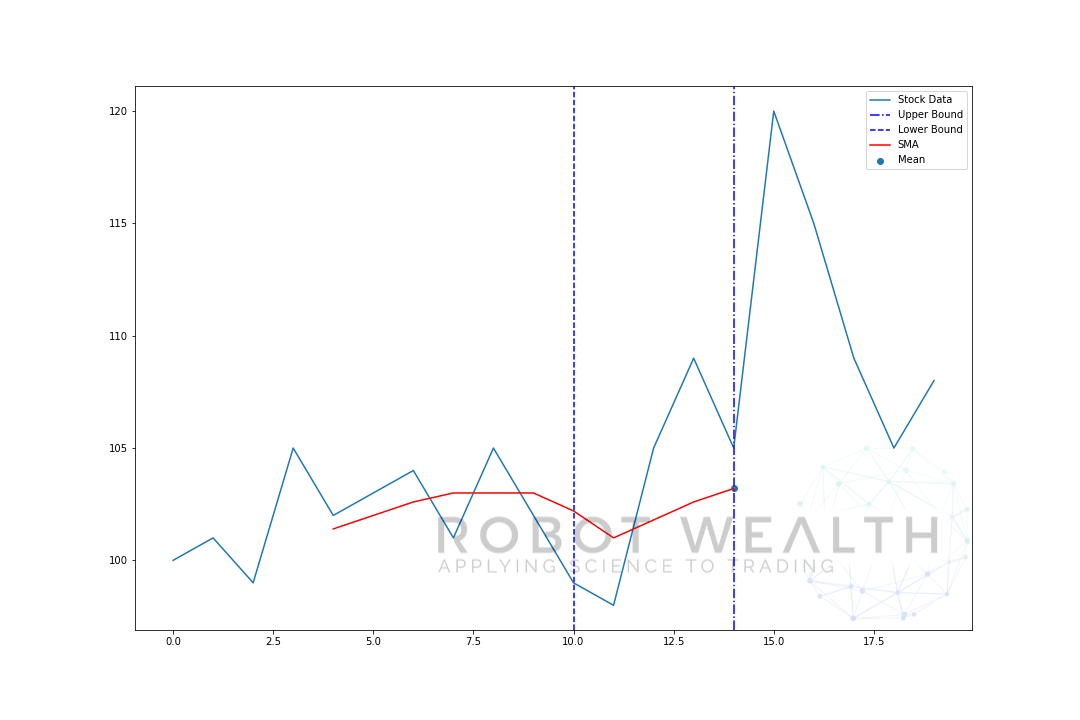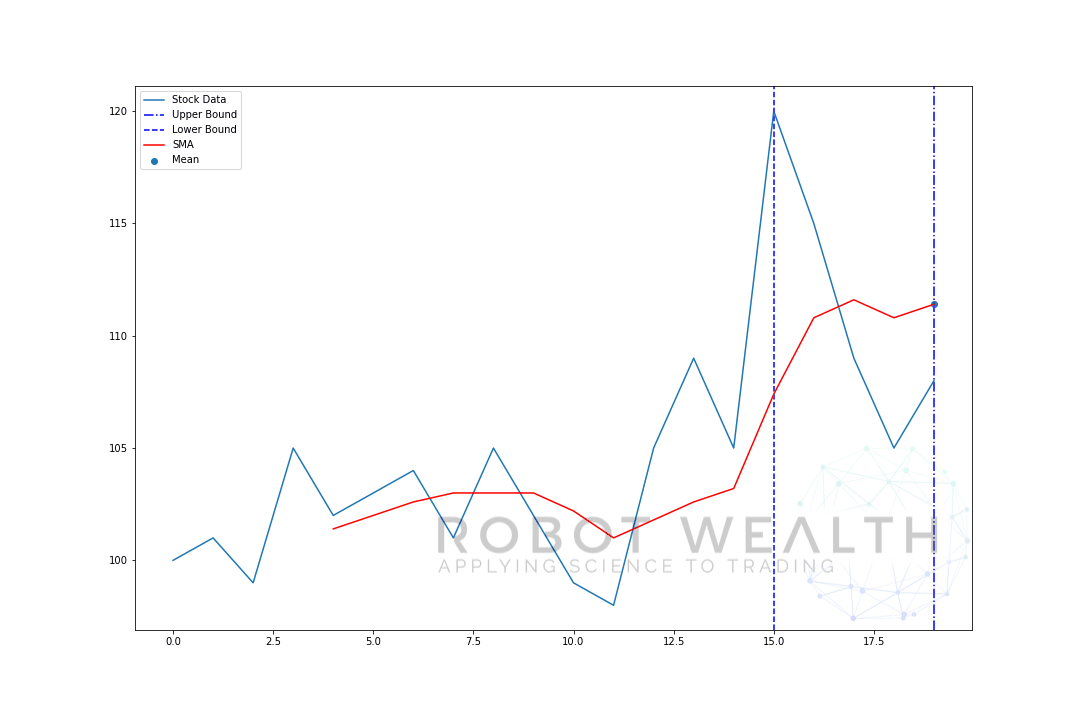
#Random stock pricesdata = #Create pandas DataFrame from listdf = pd.DataFrame(data,columns=)#Calculate a 5 period simple moving averagesma5 = df.rolling(window=5).mean()#Plotplt.plot(df,label='Stock Data')plt.plot(sma5,label='SMA',color='red')plt.legend()plt.show()
Así que vamos desglose de este gráfico.
- Tenemos 20 días de precios de acciones en este gráfico, etiquetados con Datos de acciones.
- Para cada punto en el tiempo (el punto azul) queremos saber cuál es el precio medio de 5 días.
- Los datos de stock utilizados para el cálculo son el material entre las 2 líneas verticales azules.
- Después de calcular la media de 0-5, nuestra media para el día 5 estará disponible.
- Para obtener la media del día 6, necesitamos cambiar la ventana por 1, por lo que la ventana de datos se convierte en 1-6.
Y esto es lo que se conoce como ventana móvil, el tamaño de la ventana es fijo. Todo lo que estamos haciendo es avanzar.
Como probablemente haya notado, no tenemos valores de SMA para los puntos 0-4. Esto se debe a que nuestro tamaño de ventana (también conocido como período retrospectivo) requiere al menos 5 puntos de datos para hacer el cálculo.
Ventanas en expansión
Cuando las ventanas móviles tienen un tamaño fijo, las ventanas en expansión tienen un punto de partida fijo e incorporan nuevos datos a medida que están disponibles.
Esta es la forma en que me gusta pensar sobre esto:
«¿Cuál es la media de los valores pasados de n en este momento?»- Usa ventanas enrollables aquí.
«¿Cuál es la media de todos los datos disponibles hasta este momento?»- Utilice ventanas en expansión aquí.
Las ventanas en expansión tienen un límite inferior fijo. Solo el borde superior de la ventana se enrolla hacia adelante (la ventana se hace más grande).
Visualicemos una ventana en expansión con los mismos datos de la gráfica anterior.
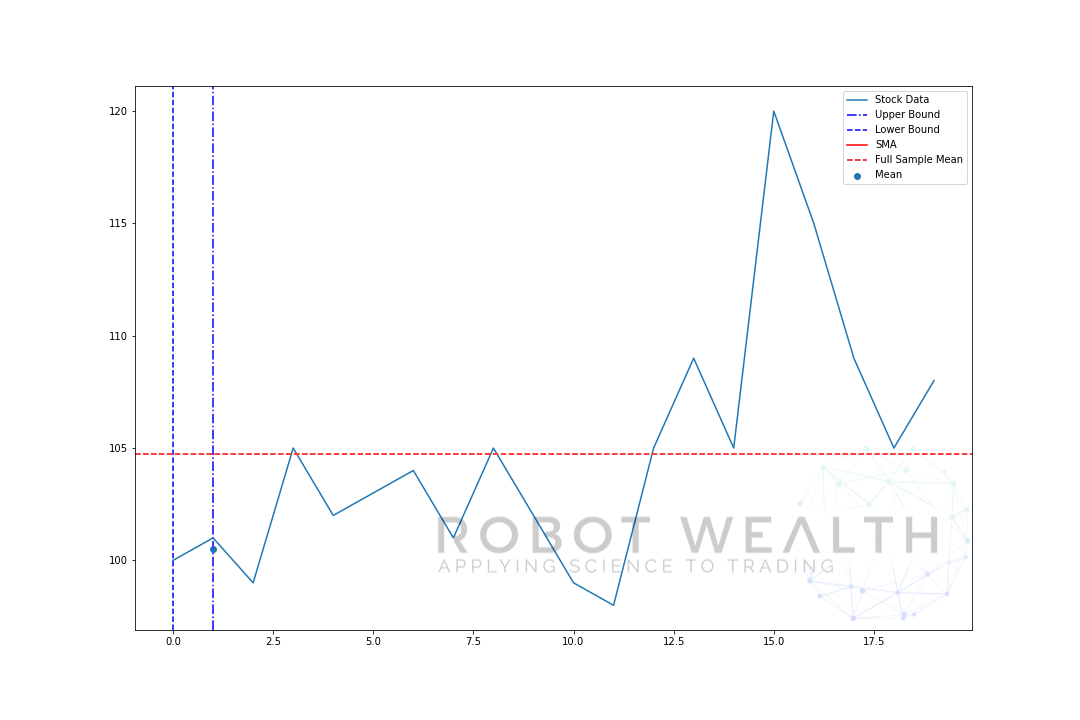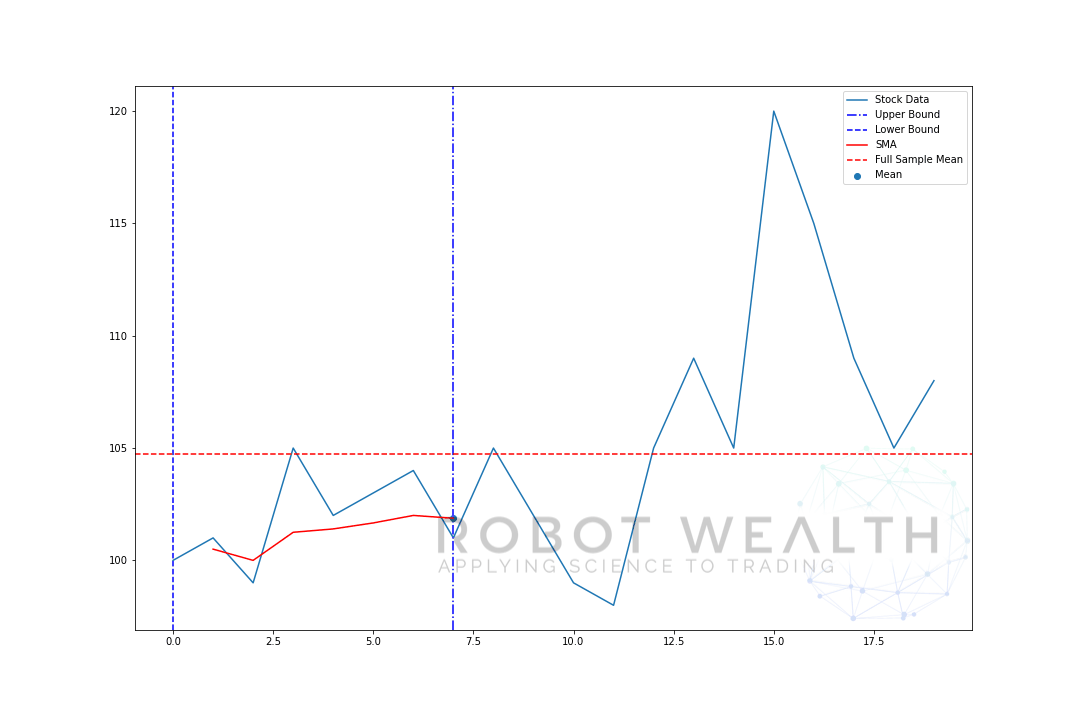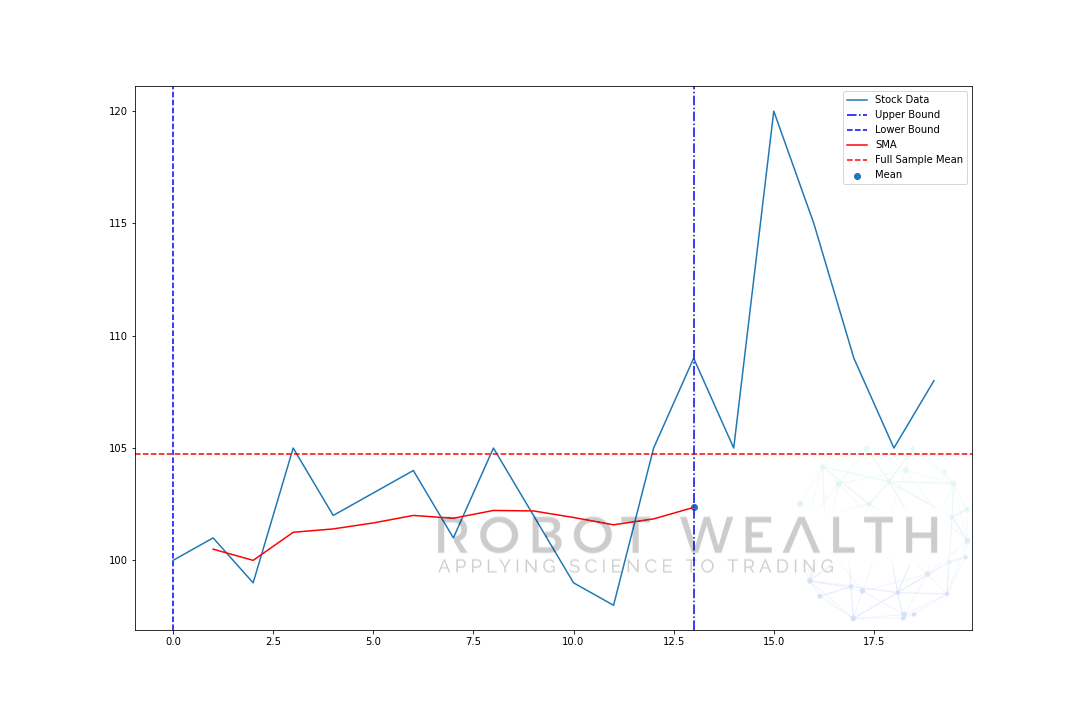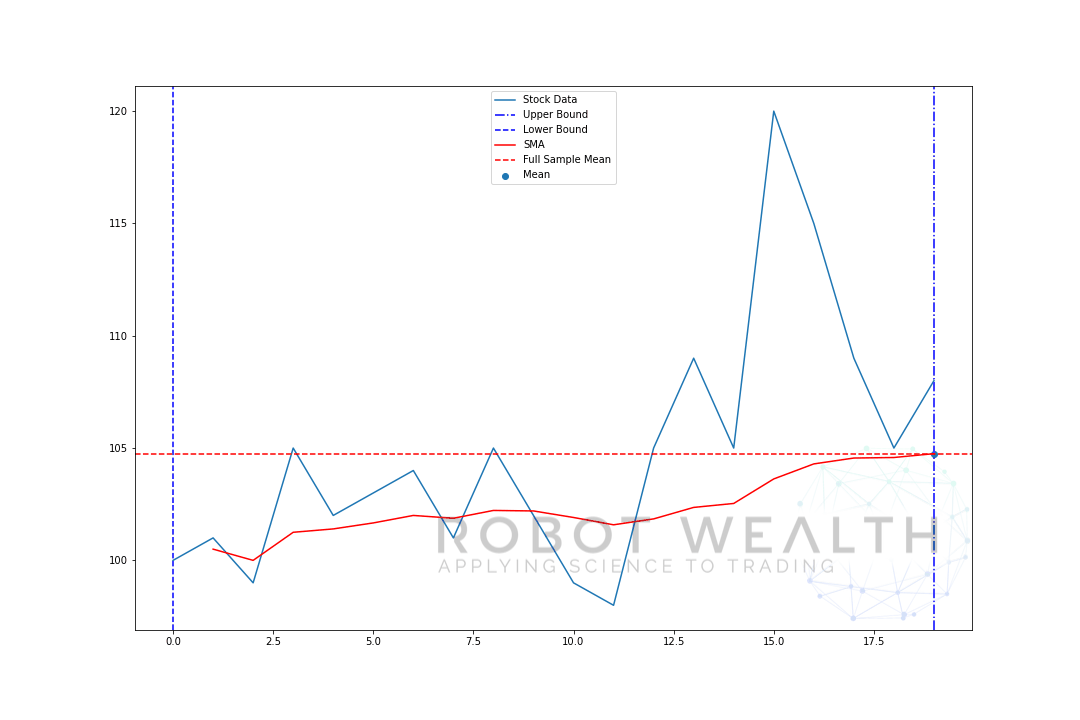
#Random stock prices data = #Create pandas DataFrame from list df = pd.DataFrame(data,columns=) #Calculate expanding window meanexpanding_mean = df.expanding(min_periods=1).mean()#Calculate full sample mean for referencefull_sample_mean = df.mean()#Plot plt.plot(df,label='Stock Data') plt.plot(expanding_mean,label='Expanding Mean',color='red')plt.axhline(full_sample_mean,label='Full Sample Mean',linestyle='--',color='red')plt.legend()plt.show()
Puede ver que al principio, el SMA está un poco nervioso. Eso es porque tenemos un menor número de puntos de datos al principio de la gráfica, y a medida que obtenemos más datos, la ventana se expande hasta que finalmente la media de la ventana en expansión converge a la media de muestra completa, porque la ventana ha alcanzado el tamaño de todo el conjunto de datos.
Resumen
Es importante no utilizar datos del futuro para analizar el pasado. Las ventanas enrollables y en expansión son herramientas esenciales para ayudar a «avanzar sus datos» para evitar estos problemas.
Si te ha gustado este probablemente como estos también…
Financiera de Manipulación de Datos en dplyr para Quant Comerciantes
el Uso de Procesamiento de Señales Digitales en Estrategias de Trading Cuantitativas
Backtesting Sesgo: se Siente Bien, Hasta estallar