A Franck-Condon Principle leírja a vibronikus átmenetek intenzitását, vagy egy foton abszorpcióját vagy emisszióját. Azt állítja, hogy amikor egy molekula elektronikus átmeneten, például ionizáción megy keresztül, a molekula nukleáris konfigurációja nem tapasztal jelentős változást. Ez annak köszönhető, hogy a magok sokkal masszívabbak, mint az elektronok, és az elektronikus átmenet gyorsabban megy végbe, mint ahogy az atommagok reagálni tudnak. Amikor a mag átrendezi magát az új elektronikus konfigurációval, az elmélet azt állítja, hogy rezgésnek kell alávetnie.
Ha úgy képzeljük el a függőleges átmenetet a talajról a gerjesztett elektronikus állapotra,mint amely egy vibrációs hullámfüggvényből következik be, amely valószínűségi eloszlást ad a magok megtalálására a tér give régiójában, akkor meghatározhatjuk egy adott rezgési szint valószínűségét az átfedő integrál \(s_{v’, v}\), amely megadja a rezgési hullámfüggvény átfedését a talajban és a gerjesztett állapotban. A\ (v’\) kvantumszámok az alapállapotra, a \(v\) kvantumszámok pedig a gerjesztett állapotra utalnak. Az átmenet valószínűsége a Condon-közelítéssel elektronikus és nukleáris részekre osztható.
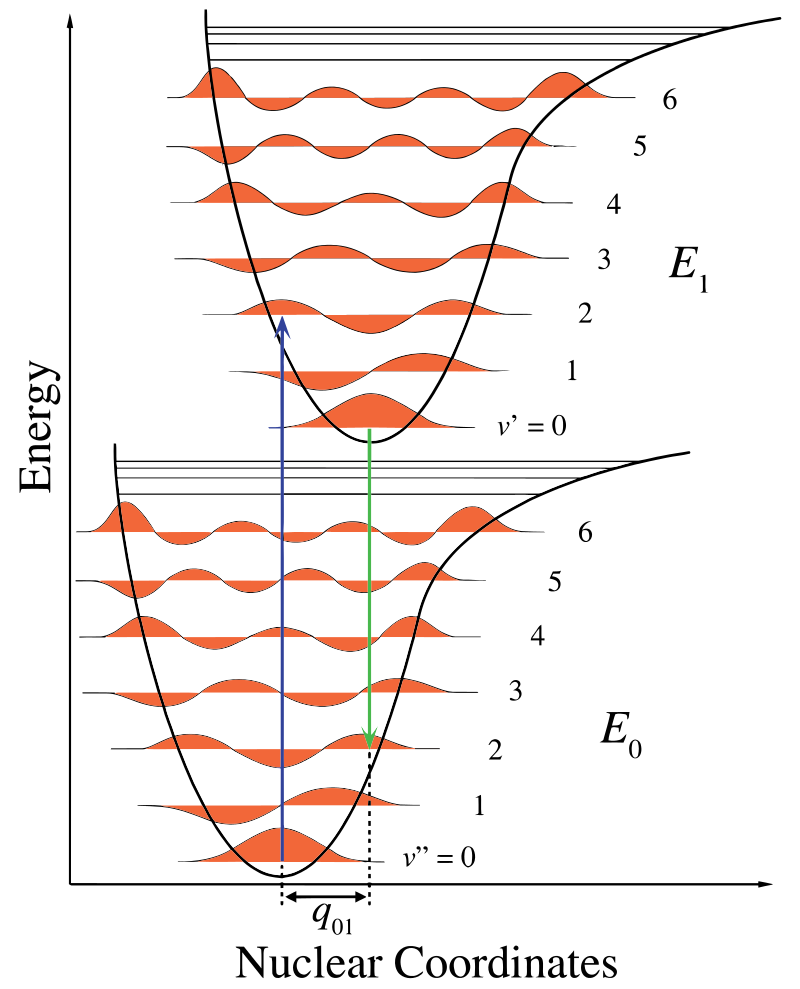
a \(\PageIndex{1}\) ábrán a magtengely az internukleáris elválasztás következményét mutatja, a vibronikus átmenetet pedig a kék és zöld függőleges nyilak jelzik. Ez az ábra három dolgot mutat be:
- az abszorpció magasabb energiaállapothoz vezet,
- a fluoreszcencia alacsonyabb energiaállapothoz vezet, és
- a nukleáris koordináták eltolódása a talaj és a gerjesztett állapot között a nukleáris kölcsönhatási potenciál új egyensúlyi helyzetét jelzi. Az a tény, hogy a fluoreszcencia nyíl rövidebb, mint az abszorpció, azt jelzi, hogy kevesebb energiája van, vagy hogy hullámhossza hosszabb.
A Klasszikus Condon közelítés
Condon közelítés az a feltételezés, hogy az elektronikus átmenet a időskála rövid a nukleáris mozgáshoz képest, így az átmenet valószínűsége fix nukleáris helyzetben kiszámítható.
ezt a rezgésváltozást a gyors elektronikus gerjesztésnek nevezett állapot alatt tartják fenn. A kapott Coulombikus erők egyensúlyt hoznak létre, amint azt az A-nak nevezett magok ábrája mutatja fordulópont. A fordulópont leképezhető úgy, hogy függőleges vonalat rajzol az alsó görbe minimumától a magasabb elektronikus állapot metszéspontjáig. Ezt az eljárást vertikális átmenetnek nevezik, és korábban a fotoelektron spektroszkópia (egy másik elektronikus spektroszcoy) összefüggésében tárgyalták..
A Franck-Condon elv magyarázza a vibrációs átmenetek relatív intenzitását azáltal, hogy a vibrációs átmenet valószínűségét összekapcsolja a vibrációs hullámfüggvények átfedésével. Megállapítja, hogy a rezgési átmenet bekövetkezésének valószínűségét a Franck-Condon átfedési integrál súlyozza:
\
A Franck-Condon közelítésen belül a magokat “rögzítettnek” tekintik az elektronikus átmenetek során. Így az elektronikus átmenetek függőleges átmeneteknek tekinthetők az elektronikus potenciális energia görbéken (vierikus átmenetek a \(\PageIndex{1}\) ábrán).
A kvantum Franck-Condon elv
A Franck-Condon elvnek mind klasszikus, mind kvantum alkalmazása van. Klasszikusan a Franck-Condon elv az a közelítés, hogy az elektronikus átmenet a legvalószínűbb, hogy a molekuláris entitásban és annak környezetében lévő magok helyzetének változása nélkül következik be. A kapott állapotot Franck–Condon állapotnak nevezzük, az átmenetet pedig vertikális átmenetnek. Ennek az elvnek a kvantummechanikai megfogalmazása az, hogy a vibronikus átmenet intenzitása arányos az átmenetben részt vevő két állapot vibrációs hullámfunkciói közötti átfedési integrál négyzetével.
A Franck-Condon elv a Born-Oppenheimer közelítésen alapul, amely lehetővé teszi az elektronikus \(q\) és a nukleáris \(Q\) hullámfüggvények elválasztását a teljes hullámfüggvény alapján.
\
mivel az átmenet operátor, \(\hat{\mu}(q)\), csak az elektronikus alkatrésztől függ, a nukleáris komponensek elválaszthatók az átmeneti pillanat integráljától, amely meghatározza az átmenet bekövetkezésének valószínűségét:
&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nukleáris átfedés}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, I} \Rangle \end{align}\]
ha a nukleáris átfedési integrál nulla ebben az átmenetben, akkor az átmenet nem figyelhető meg, függetlenül az elektronikus tényező nagyságától.
\(s_{00}\) a harmonikus oszcillátor modellen belül értékelt átmenet
a nulla-nulla átmenet nukleáris átfedése \(s_{00}\) egyszerűen kiszámítható a harmonikus oszcillátor hullámfunkcióinak Gauss-formájának meghatározásával.
a nulla pontú hullámfüggvény a földi elektronikus állapotban
\
a gerjesztett elektronikus állapotban a nulla pontú hullámfüggvény
\
ahol
- \(\alpha = \dfrac{\sqrt{MK}}{\HBAR}\)
- \(r_e\) az egyensúlyi kötés hossza a földi elektronikus állapotban
- \(q_e\) az egyensúlyi kötés hossza a gerjesztett elektronikus állapotban
a nukleáris átfedési integrál
\
a kitevő a \(\ref{FC1}\) egyenletben kibővíthető mint
\
és használjuk a
\
és
\
az integrálon belüli négyzet helyettesítésére és kitöltésére. Kifejezhetjük
\.\]
így az integrál a \(\ref{FC2}\) egyenletben
\
az integrál Gauss-integrál. Megmutathatjuk, hogy ha hagyjuk \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\), akkor \(dz = \sqrt{\alpha} dR\) és az integrál lesz
\
Ez az integrál már megoldódott, az integrálok táblázatából az egyenlet \(\ref{FC3}\) lesz
\
ugyanezt az eljárást követnénk annak kiszámításához, hogy a föld nulladik szintű rezgésének átfedése a gerjesztett állapot első gerjesztett vibrációs szintjéig terjed: \(s_{01}\).
\(s_{01}\) a harmonikus oszcillátor modellen belül kiértékelt átmenet
a nulla alapállapot szint (\(v=0\)) átfedésének kiszámításához az első gerjesztett állapot szinttel (\(v’=1\)) A Hermite polinomot használjuk \(H_1(x) =2x\) a gerjesztett állapot hullámfüggvényének leírására (lásd itt a harmonikus oszcillátor hullámfunkcióinak áttekintését). Itt \(x = \ sqrt {\alpha} (R-Q_e)\).
\
a nulla pontú hullámfüggvény a földi elektronikus állapotban
\
az első gerjesztett állapotú hullámfüggvény a gerjesztett elektronikus állapotban
\
a nulla alapállapot szint átfedése az első gerjesztett állapot szinttel (\(\ref{fc01}\) egyenlet) ekkor
\
és
\
ugyanazok a helyettesítések hajthatók végre, mint fent, így az integrál írható (nem látható és a házi feladatokban kell bemutatni) és a végeredmény:
\
folytathatnánk és kiszámolhatnánk a nulladik szint átfedését az alapállapotban az összes magasabb fényrezgési szinttel: \(s_{02}\), \(s_{03}\) stb. Minden kifejezés egy eltérő energiájú átmenetnek felel meg, mivel a rezgési szintek különböző energiákkal rendelkeznek. Az abszorpciós sáv ezután a különböző szintek közötti átmenetek progressziója (Franck-Condon progressziója) jelenik meg, mindegyik saját valószínűséggel.
Franck-Condon progresszió
ahhoz, hogy megértsük a fenti képlet jelentőségét Az FC tényezőre, vizsgáljuk meg a talaj és a gerjesztett állapot potenciális energia felületét \(T = 0\) Kelvin. Az alábbiakban két állapot van elválasztva 8000 cm-1 energiával. Ez az energia szétválasztása a potenciális kutak alja között, de a megfelelő nulla pont energiaszintek között is. Tegyük fel, hogy a rezgési mód hullámszáma 1000 cm-1, és hogy a kötés hossza megnő annak a ténynek köszönhetően, hogy egy elektront eltávolítanak egy kötési pályáról, és elektronikus gerjesztéssel egy kötésgátló pályára helyezik.
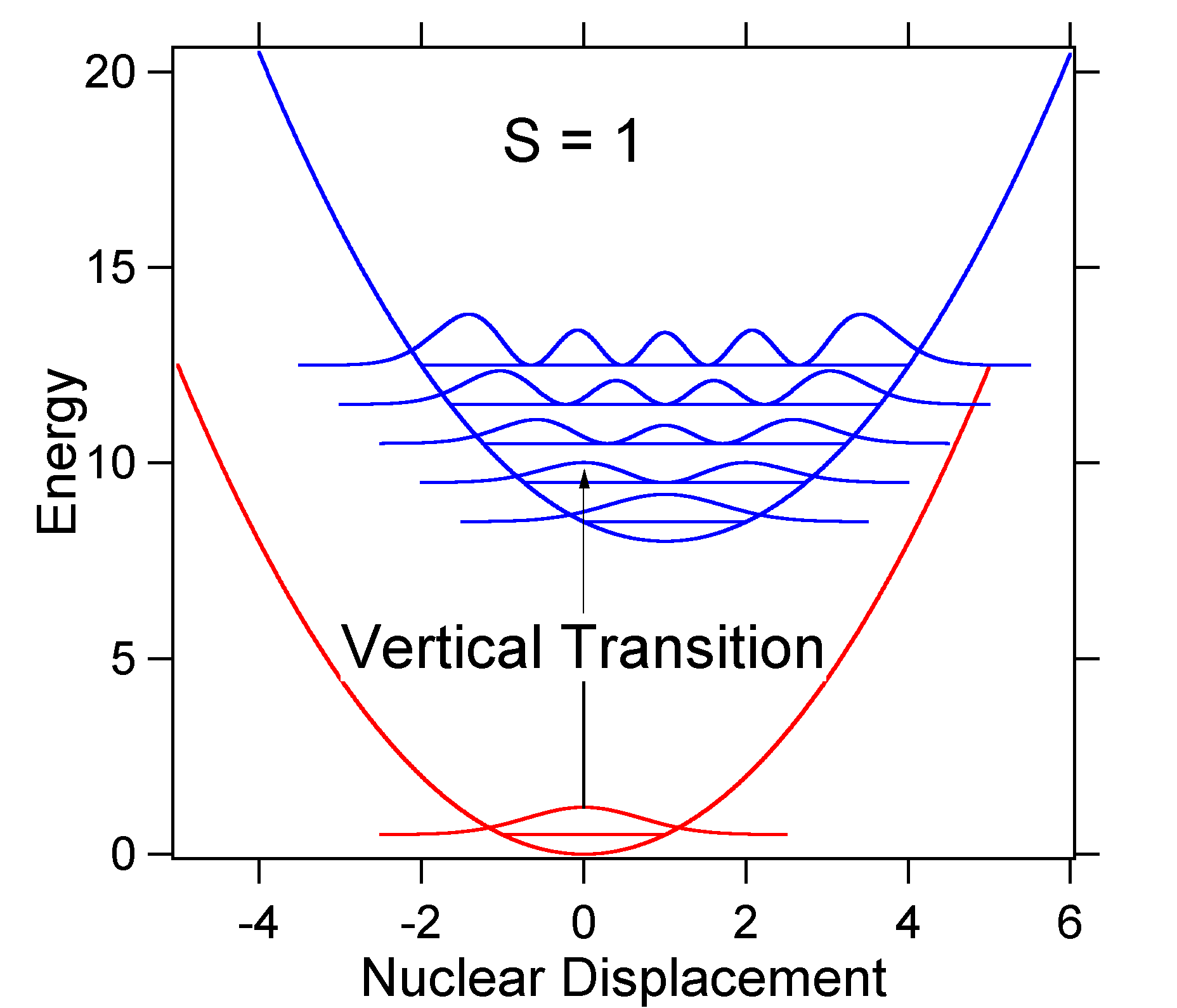
A Franck-Condon faktor fenti modellje szerint létrehoznánk egy” stick ” spektrumot (\(\PageIndex{3}\) ábra), ahol minden vibrációs átmenet végtelenül keskeny, és az átmenet csak akkor következhet be, ha \(E = h\nu\) pontosan. Például a potenciális energia felületeket S = 1-re adtuk meg, és az átmenet valószínűségét minden szinten az alábbi ábrán látható botok (fekete) adják meg.
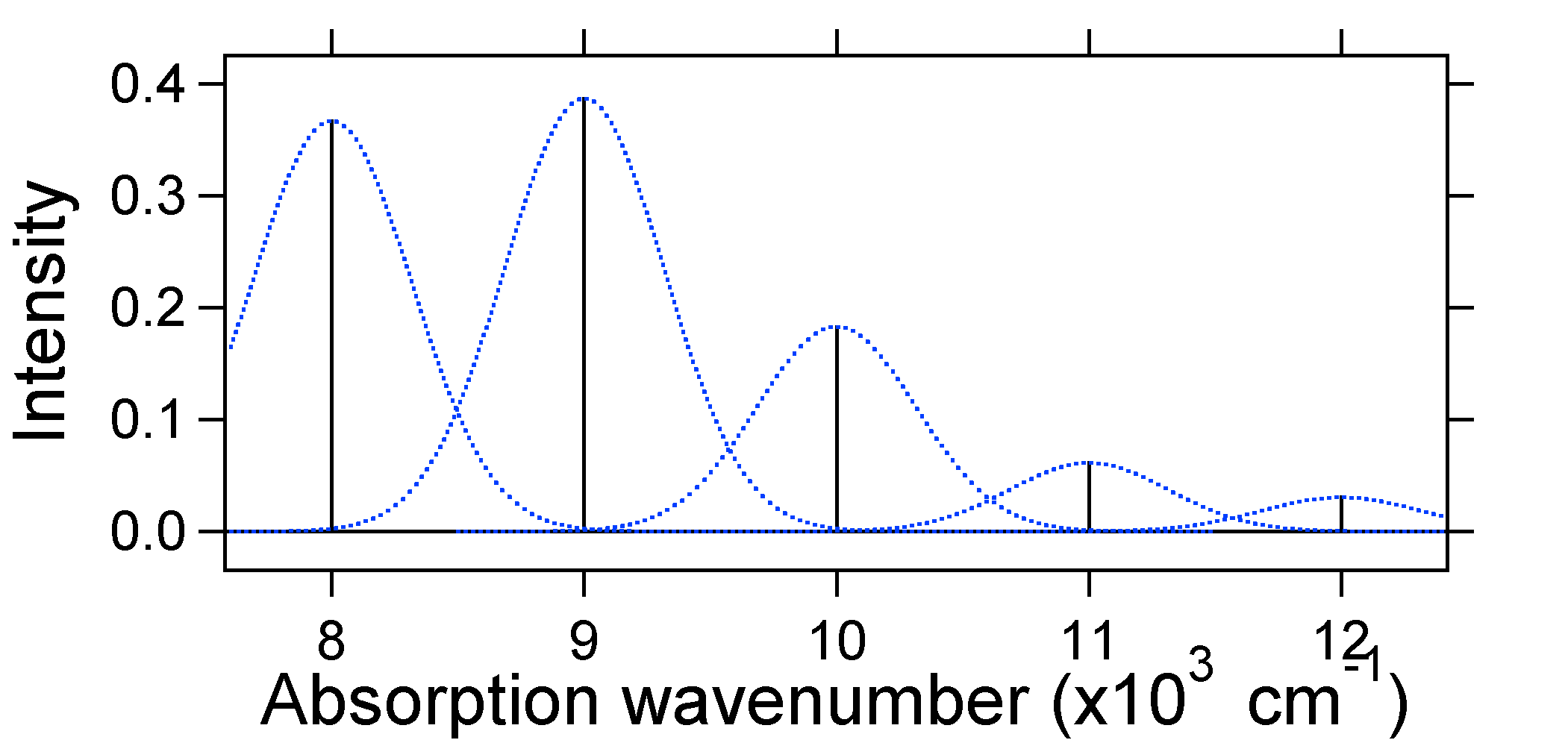
az egyes botokat körülvevő pontozott Gauss-ok valósághűbb képet adnak arról, hogy hogyan kell kinéznie az abszorpciós spektrumnak. Ebben az első helyen minden energiaszint (Bot) bizonyos szélességet kap az a tény, hogy az állam véges élettartammal rendelkezik. Az ilyen kiszélesedést homogén kiszélesedésnek nevezzük, mivel az együttes összes molekuláját hasonló módon érinti. Az egyes molekulák környezetében tapasztalható kis különbségek miatt is bővül. Ezt a fajta szélesítést inhomogén szélesítésnek nevezzük. Eredetétől függetlenül a fenti modell Gauss-féle szélesítéssel készült
a talaj és a gerjesztett állapot közötti magkiszorítás határozza meg az abszorpciós spektrum alakját. Vizsgáljuk meg mind a kisebb, mind a nagy gerjesztett állapot elmozdulását. If \(S=!) és a potenciális energiafelületek ebben az esetben a következők:
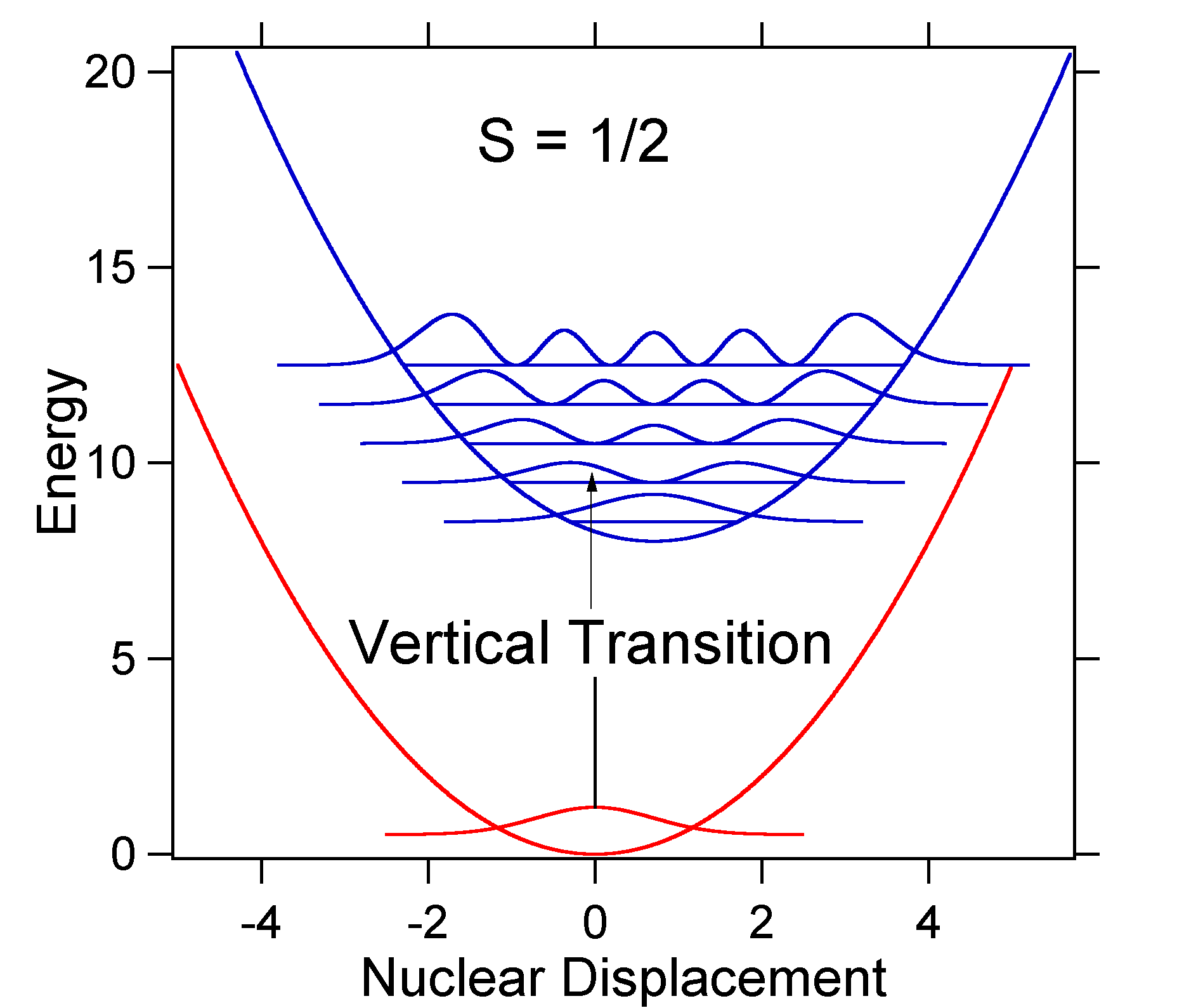
For this case the “stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
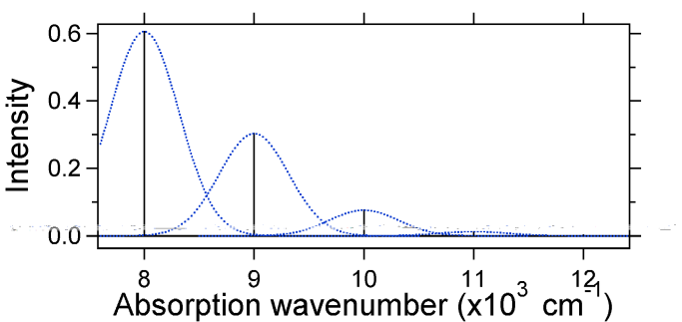
vegye figyelembe, hogy a nulla-nulla vagy \(s_{0,0}\) vibrációs átmenet sokkal Nagy abban az esetben, ha az elmozdulás kicsi.
általános szabályként a\ (S\) állandó adja meg a\ (v = 2\) átmenet intenzitásának arányát a\ (v = 1\) átmenethez. Ebben az esetben a \(S = 0,5\) óta a \(v=2\) átmenet 0,5 A \(v=1\) átmenet intenzitása.
nagyobb elmozdulás példájaként a potenciális energiafelületek eloszlása S = 2 esetén az alábbiakban látható.
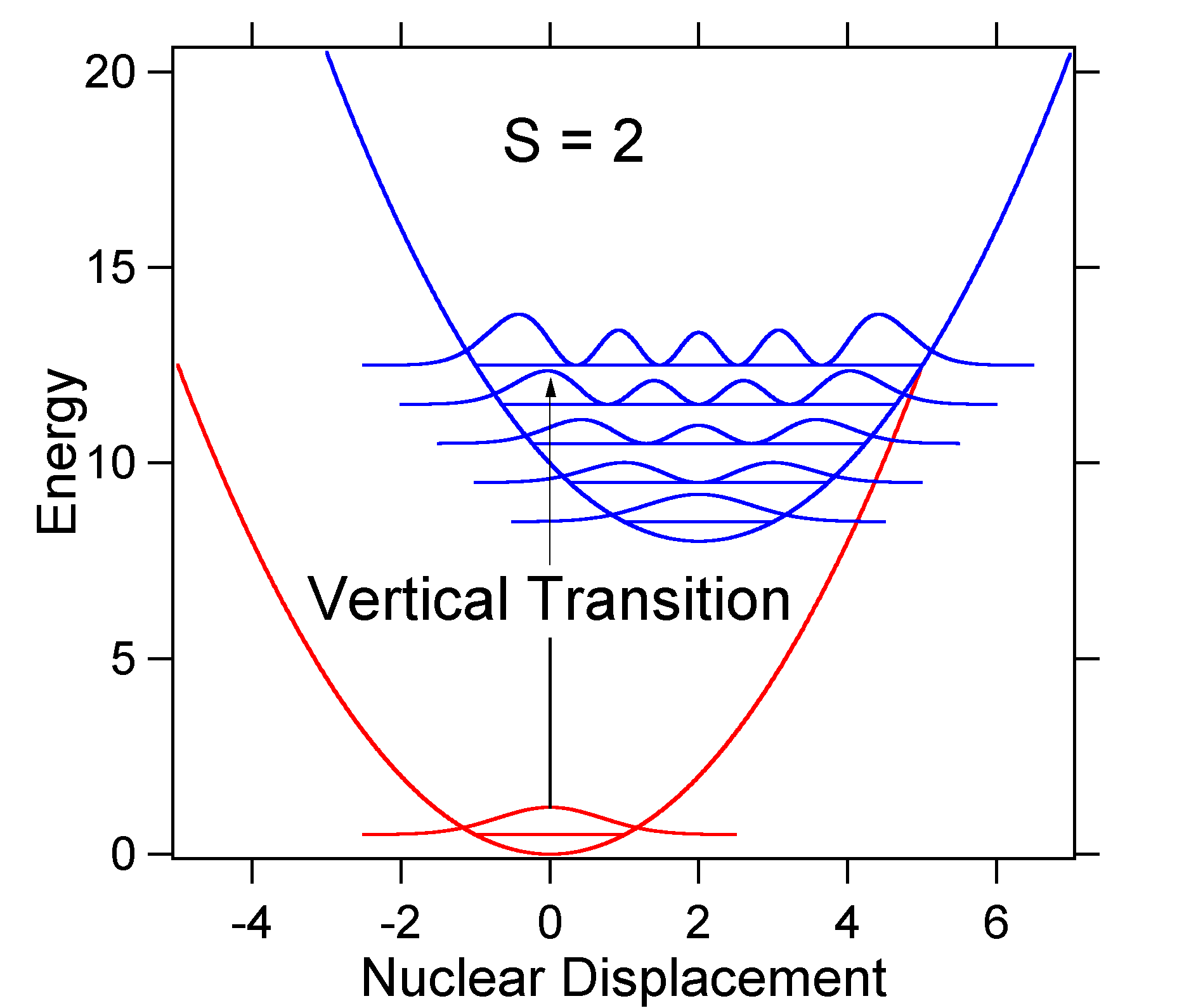
a nagyobb elmozdulás az alapállapot szintjének csökkent átfedését eredményezi a gerjesztett állapot v = 0 szintjével. A maximális intenzitást magasabb rezgési szinteken érik el, amint azt a botspektrum mutatja.
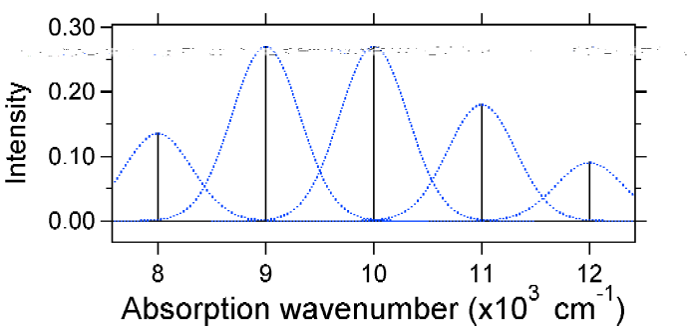
az alábbiakban ábrázolt abszorpciós spektrumok mindegyike azonos integrált intenzitással rendelkezik, azonban alakjuk megváltozik a gerjesztett állapotú potenciális energiafelület eltérő elmozdulási mértéke miatt.
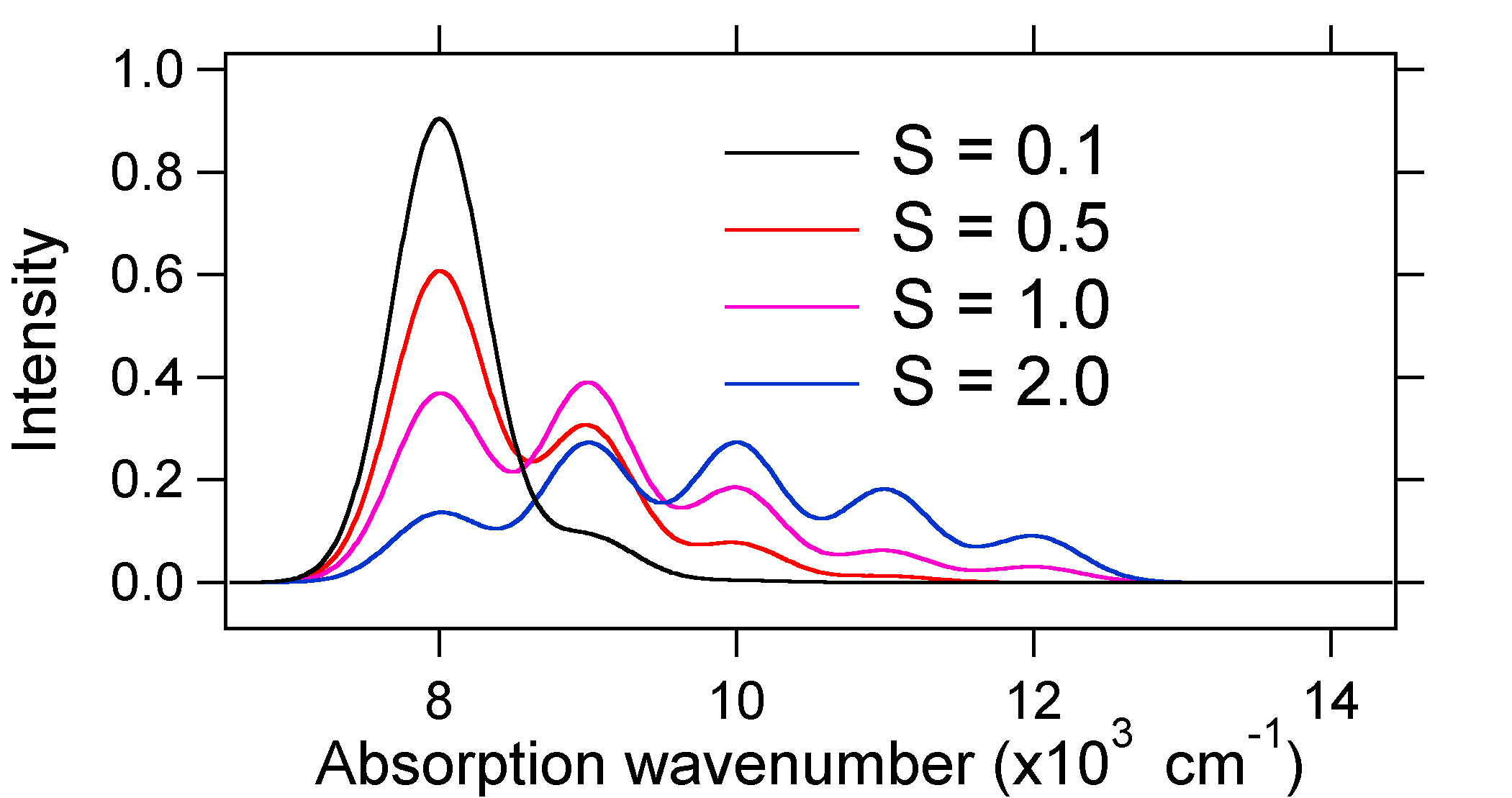
tehát a relatív vibrációs sáv intenzitásának jellege meg tudja mondani, hogy van-e elmozdulás az egyensúlyi nukleáris koordináta, amely átmenetet kísér. Mikor növekszik a kötvény hossza (azaz \(Q_e > R_e\))? Ez akkor fordul elő, amikor egy elektront egy kötő molekulapályáról egy nem kötő vagy anti-kötő molekulapályára mozdítanak elő (vagyis amikor a kötési sorrend kevésbé gerjesztett állapotban van, mint az alapállapot).
- nem kötő molekulapálya \(\rightarrow\) kötő molekulapálya
- Kötésgátló molekulapálya \(\rightarrow\) kötő molekulapálya
- Kötésgátló molekulapálya \(\rightarrow\) nem kötő molekulapálya
röviden, ha a kötés sorrendje gerjesztett állapotban alacsonyabb, mint alapállapotban, akkor \(Q_e > r_e\); a kötéshossz növekedése akkor következik be, amikor ez megtörténik.
- J. M. Luis, D. M. Bishop, B. Kirtman. Más megközelítés a Franck–Condon tényezők kiszámításához, beleértve az anharmonicitást is. J. Kémia. Phys., 120 (2004), 813-822.Atkins, Peter és Julio De Paula. Fizikai kémia az élettudományok számára. 2006. New York, NY: W. H. Freeman és társai. o.563-564
- Franck-Condon elv. 1996, 68, 2243. IUPAC kémiai terminológia összefoglalója 2. kiadás (1997). www.iupac.org/goldbook/F02510.pdf
- E. Rabinowitch és Govindjee. Fényelnyelés és az energia gerjesztésének sorsa. 1969. Franck-Condon Elv. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
közreműködők
- Matthe Zi Ziering
-
Stefan Franzen (Észak-Karolinai Állami Egyetem)