a mély maradék hálózatok (ResNet) viharral vette át a mély tanulás világát, amikor a Microsoft Research kiadta a mély maradék tanulást a Képfelismeréshez. Ezek a hálózatok 1. helyezést értek el az ImageNet és a COCO 2015 versenyek mind az öt fő pályáján, amelyek kiterjedtek a képosztályozásra, az objektumfelismerésre és a szemantikai szegmentálásra. A Resnetek robusztusságát azóta különböző vizuális felismerési feladatok, valamint a beszédet és a nyelvet érintő nem vizuális feladatok bizonyították. Phd disszertációm kutatásában más mély tanulási modellek mellett a ResNet-et is használtam.
Ez a bejegyzés összefoglalja az alábbi három cikket, amelyeket mind a ResNet feltalálója, Kaiming He írt vagy közösen írt, mert úgy gondolom, hogy az eredeti dokumentumok adják a modell/hálózatok leg intuitívabb és legrészletesebb magyarázatát. Remélhetőleg ez a bejegyzés segíthet jobban megérteni a maradék hálózatok lényegét.
- mély maradék tanulás a Képfelismeréshez
- Identitásleképezések mély maradék hálózatokban
- aggregált maradék transzformáció mély neurális hálózatokhoz
- intuíció mély maradék hálózaton (stackoverflow ref)
- mély maradék tanulás a Képfelismeréshez
- probléma
- lásd a degradációt működés közben:
- hogyan lehet megoldani?
- intuíció a maradék blokkok mögött:
- teszt esetek:
- hálózat tervezése:
- eredmények
- mélyebb tanulmányok
- megfigyelések
- Identitásleképezések mély maradék hálózatokban
- Bevezetés
- mély maradék hálózatok elemzése
- az identitás fontossága ugrás kapcsolatok
- kísérletek Ugrás kapcsolatok
- aktiválási függvények használata
- kísérletek az Aktiválásra
- következtetés
- aggregált maradék transzformáció a mély neurális hálózatokhoz
- Bevezetés
- módszer
- kísérletek
intuíció mély maradék hálózaton (stackoverflow ref)
a maradék blokk a következőképpen jelenik meg:
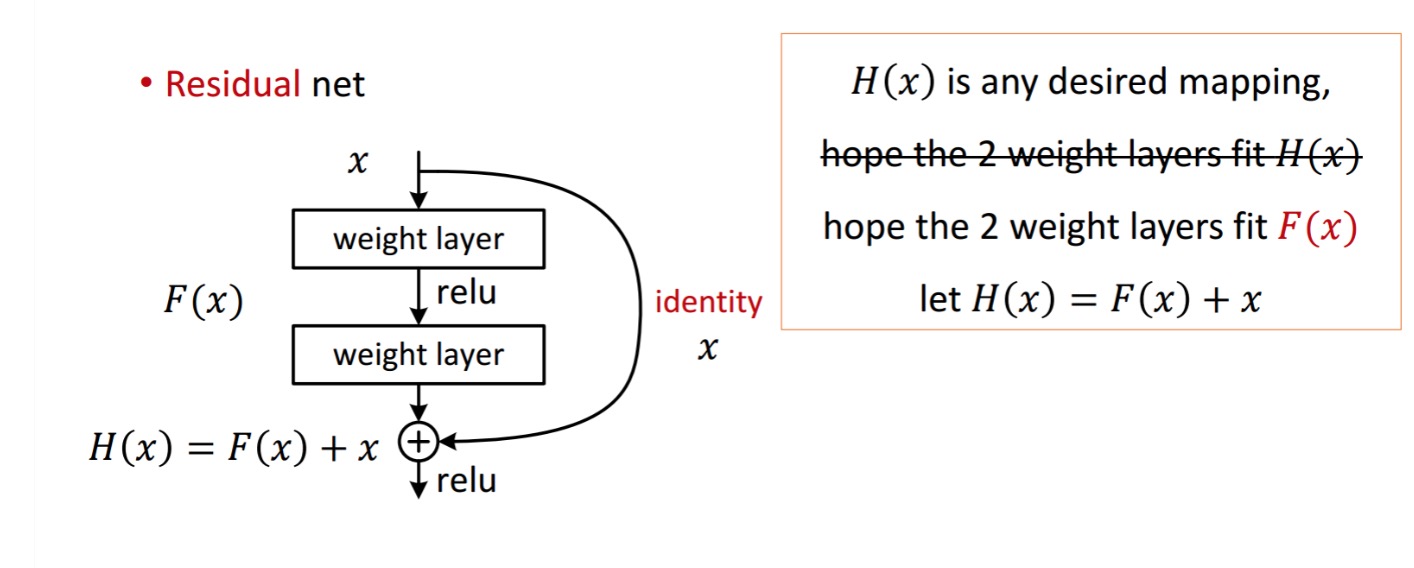
tehát a bemutatott maradék egység két Súlyréteggel történő feldolgozással érhető el. Aztán hozzáteszi, hogy megszerezni . Most, tegyük fel, hogy ez az ideális előrejelzett kimenet, amely megfelel a földi igazságnak. Mivel a kívánt megszerzése a tökéletes megszerzésétől függ . Ez azt jelenti, hogy a maradék egység két súlyrétegének valóban képesnek kell lennie a kívánt előállítására , akkor garantált az ideális elérése.
a következőkből áll.
a következőkből áll.
a szerzők feltételezik, hogy a maradék leképezés (azaz ) könnyebben optimalizálható, mint . Egy egyszerű példával szemléltetve tegyük fel, hogy az ideális . Ezután a közvetlen leképezéshez nehéz lenne megtanulni az identitás leképezését, mivel a nemlineáris rétegek halmaza az alábbiak szerint van.
tehát az identitásleképezés közelítése ezekkel a súlyokkal és Relusokkal a közepén nehéz lenne.
most, ha meghatározzuk a kívánt leképezést , akkor csak szükségünk van a következők szerint.
A fentiek elérése egyszerű. Csak állítsa be a súlyt nullára, és nulla kimenetet kap. Add vissza, és megkapja a kívánt leképezést.
mély maradék tanulás a Képfelismeréshez
probléma
amikor a mélyebb hálózatok konvergálni kezdenek, lebomlási probléma merült fel: a hálózati mélység növekedésével a pontosság telítődik, majd gyorsan romlik.
lásd a degradációt működés közben:
Vegyünk egy sekély hálózatot és annak mélyebb megfelelőjét további rétegek hozzáadásával.
legrosszabb eset: a Deeper model korai rétegei helyettesíthetők sekély hálózattal, a fennmaradó rétegek pedig csak identitásfüggvényként működhetnek (bemenet egyenlő a kimenettel).
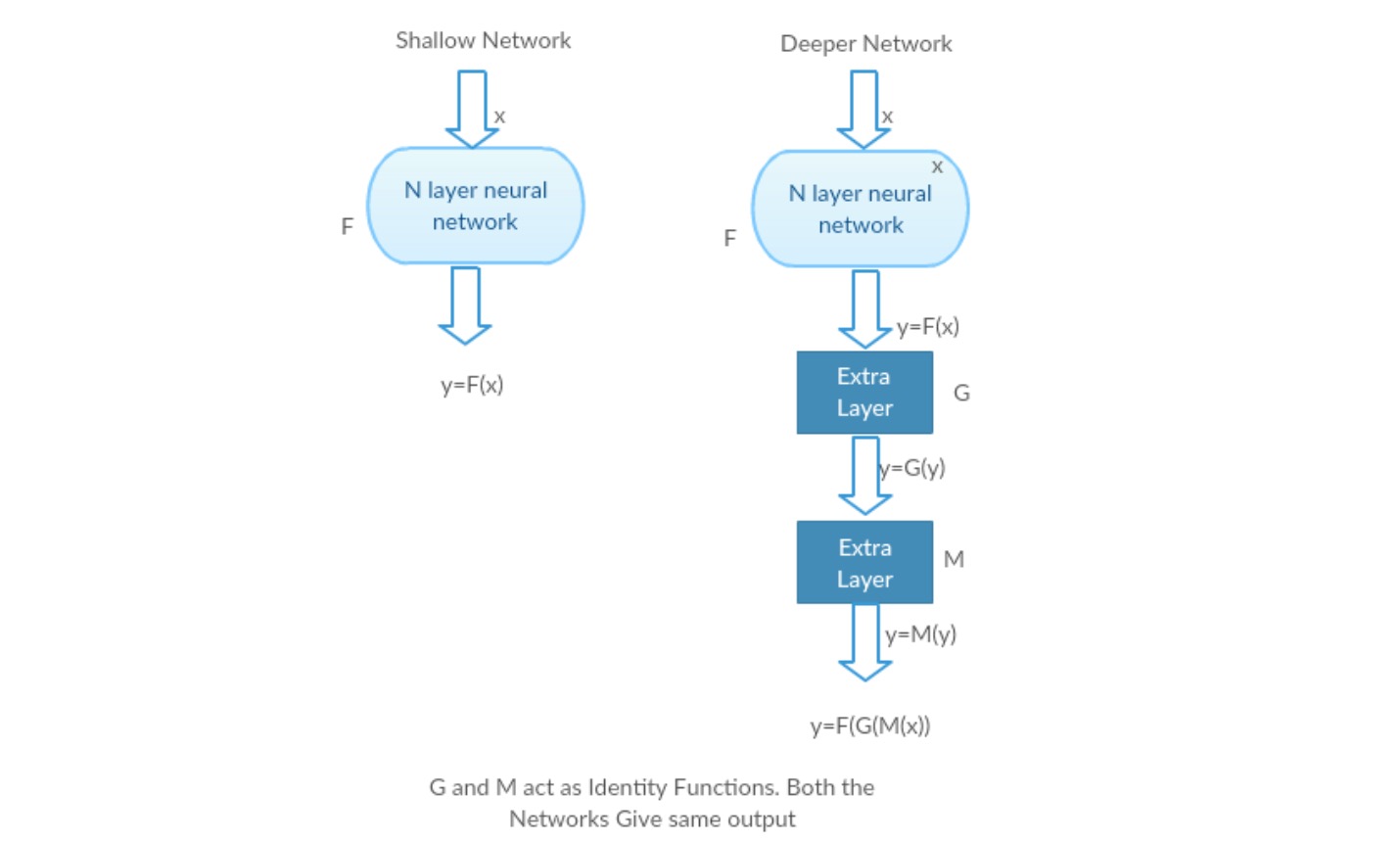
kifizetődő forgatókönyv: a mélyebb hálózatban a további rétegek jobban megközelítik a leképezést, mint a sekélyebb számláló része, és jelentős mértékben csökkentik a hibát.
kísérlet: A legrosszabb esetben mind a sekély hálózatnak, mind a mélyebb változatnak ugyanolyan pontosságot kell adnia. A kifizetődő forgatókönyv esetén a mélyebb modellnek jobb pontosságot kell adnia, mint a sekélyebb számláló része. De a jelenlegi megoldóinkkal végzett kísérletek azt mutatják, hogy a mélyebb modellek nem teljesítenek jól. Tehát a mélyebb hálózatok használata rontja a modell teljesítményét. Ezek a dokumentumok megpróbálják megoldani ezt a problémát a mély maradék tanulási keretrendszer segítségével.
hogyan lehet megoldani?
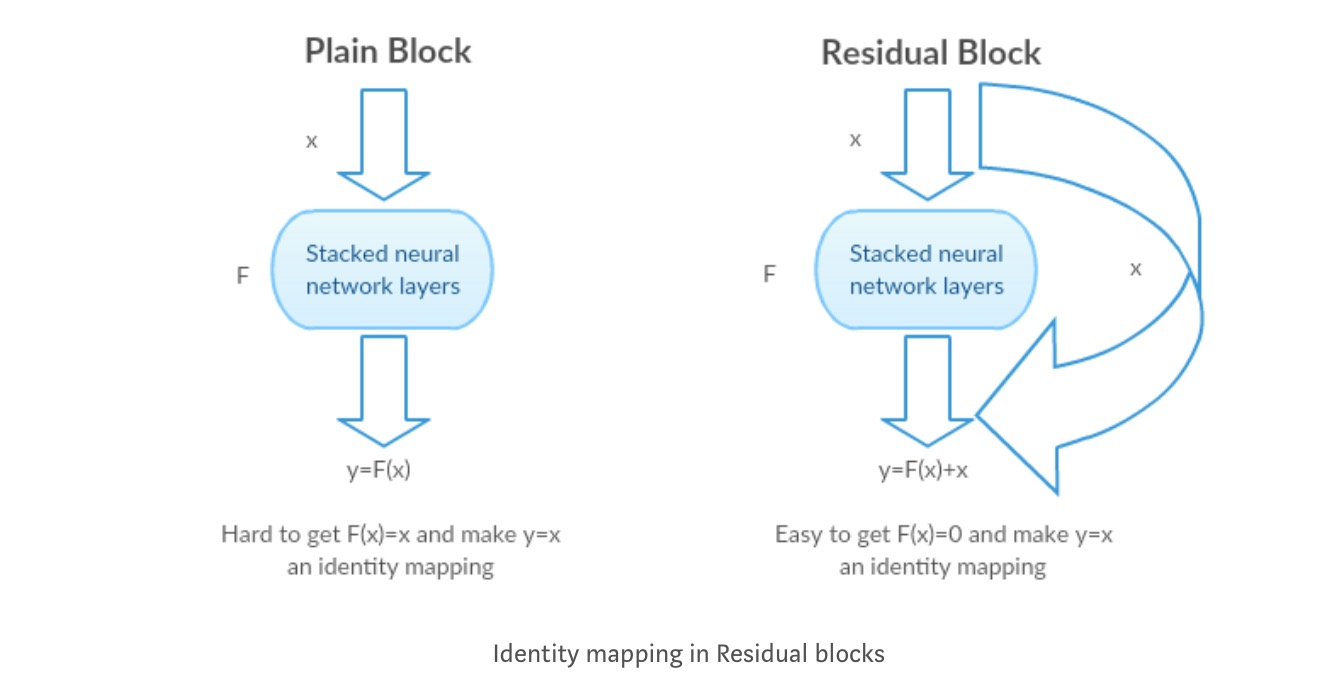
ahelyett, hogy megtanulná a függvény közvetlen leképezését (néhány halmozott nemlineáris réteg). Határozzuk meg a maradék függvényt, amely átformálható, ahol és képviseli a halmozott nemlineáris rétegeket, illetve az identitásfüggvényt (input=output).
a szerző hipotézise az, hogy könnyű optimalizálni a maradék leképezési funkciót, mint az eredeti, nem hivatkozott leképezés optimalizálása .
intuíció a maradék blokkok mögött:
vegyük példaként az identitásleképezést (pl. ). Ha az identitásleképezés optimális, akkor a maradványokat könnyen nullára () állíthatjuk, mint hogy az identitásleképezést () egy nemlineáris réteg kötegével illesszük. Egyszerű nyelven nagyon könnyű olyan megoldást találni, mint a nemlineáris cnn rétegek függvényként való használata (Gondolj bele). Tehát ezt a funkciót nevezik a szerzők maradék funkciónak.
a szerzők számos tesztet végeztek hipotézisük tesztelésére. Nézzük meg most mindegyiket.
teszt esetek:
Vegyünk egy sima hálózatot (VGG fajta 18 rétegű Hálózat) (Hálózat-1) és annak mélyebb változatát (34 rétegű, hálózat-2), és adjunk hozzá maradék rétegeket a hálózathoz-2 (34 réteg maradék kapcsolatokkal, hálózat-3).
hálózat tervezése:
- többnyire 3*3 szűrőt használjon.
- le mintavétel CNN rétegekkel a stride 2-vel.
- globális átlagos pooling réteg és egy 1000-utas teljesen csatlakoztatott réteg Softmax a végén.

kétféle maradék kapcsolat létezik:
I. az azonosító parancsikonok () közvetlenül használhatók, ha a bemenet () és a kimenet () azonos méretűek.
II. amikor a méretek megváltoznak, A) A parancsikon továbbra is identitásleképezést hajt végre, extra nulla bejegyzésekkel a megnövelt dimenzióval. B) a vetítési parancsikont a dimenzió illesztésére használják (1*1 conv) a következő képlet segítségével
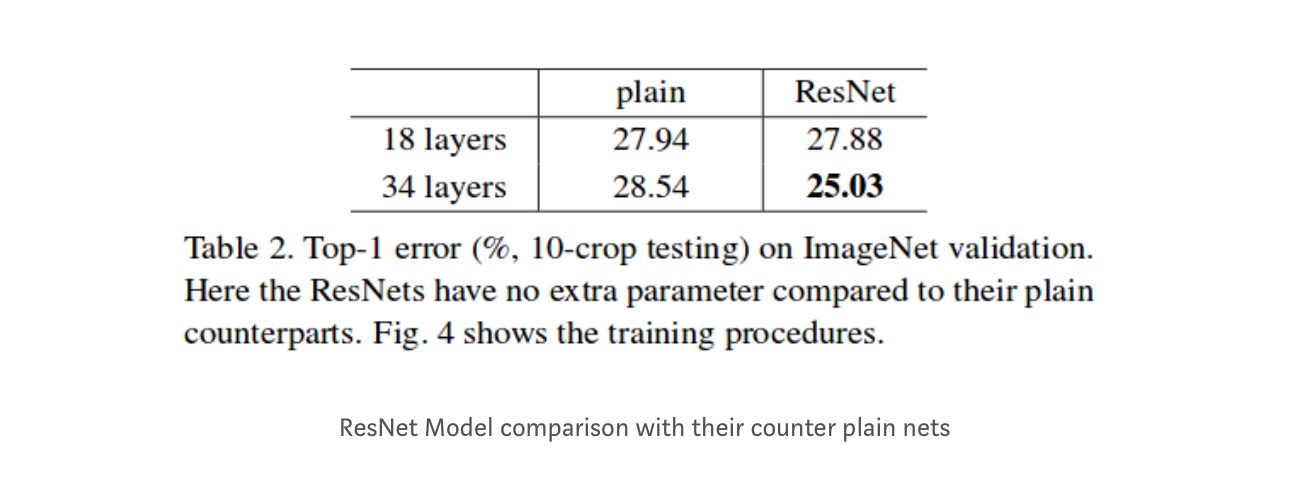
eredmények
annak ellenére, hogy a 18 rétegű hálózat csak az altér a 34 rétegű hálózatban, még mindig jobban teljesít. A ResNet jelentősen felülmúlja a hálózatot, ha a hálózat mélyebb
mélyebb tanulmányok
ezenkívül további hálózatokat is vizsgálnak:

minden ResNet blokk vagy 2 réteg mély (használt kis hálózatokban, például ResNet 18, 34) vagy 3 réteg mély( ResNet 50, 101, 152).
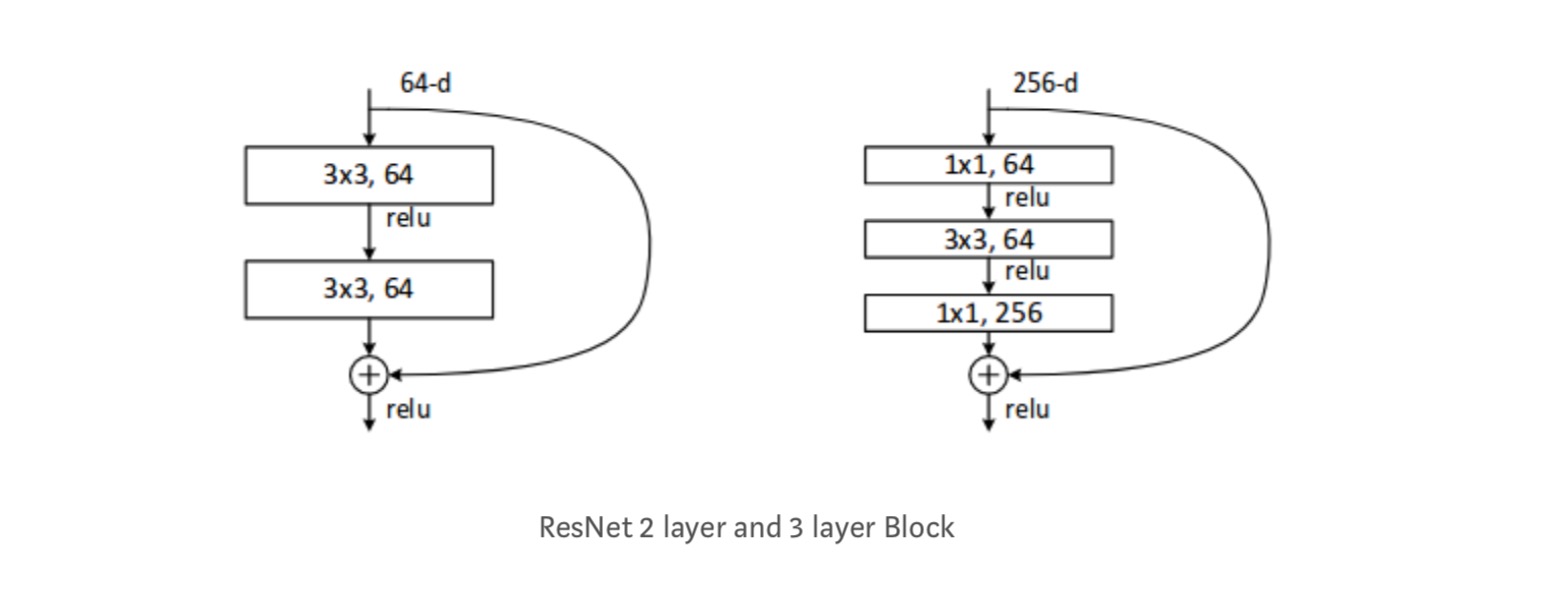
megfigyelések
- a ResNet hálózat gyorsabban konvergál, mint a sima számláló része.
- identitás vs vetítés shorcuts. Nagyon kis inkrementális nyereség vetítési parancsikonok (egyenlet-2) minden rétegben. Tehát az összes ResNet blokk csak azonossági parancsikonokat használ, a vetítési parancsikonokkal csak akkor, ha a méretek megváltoznak.
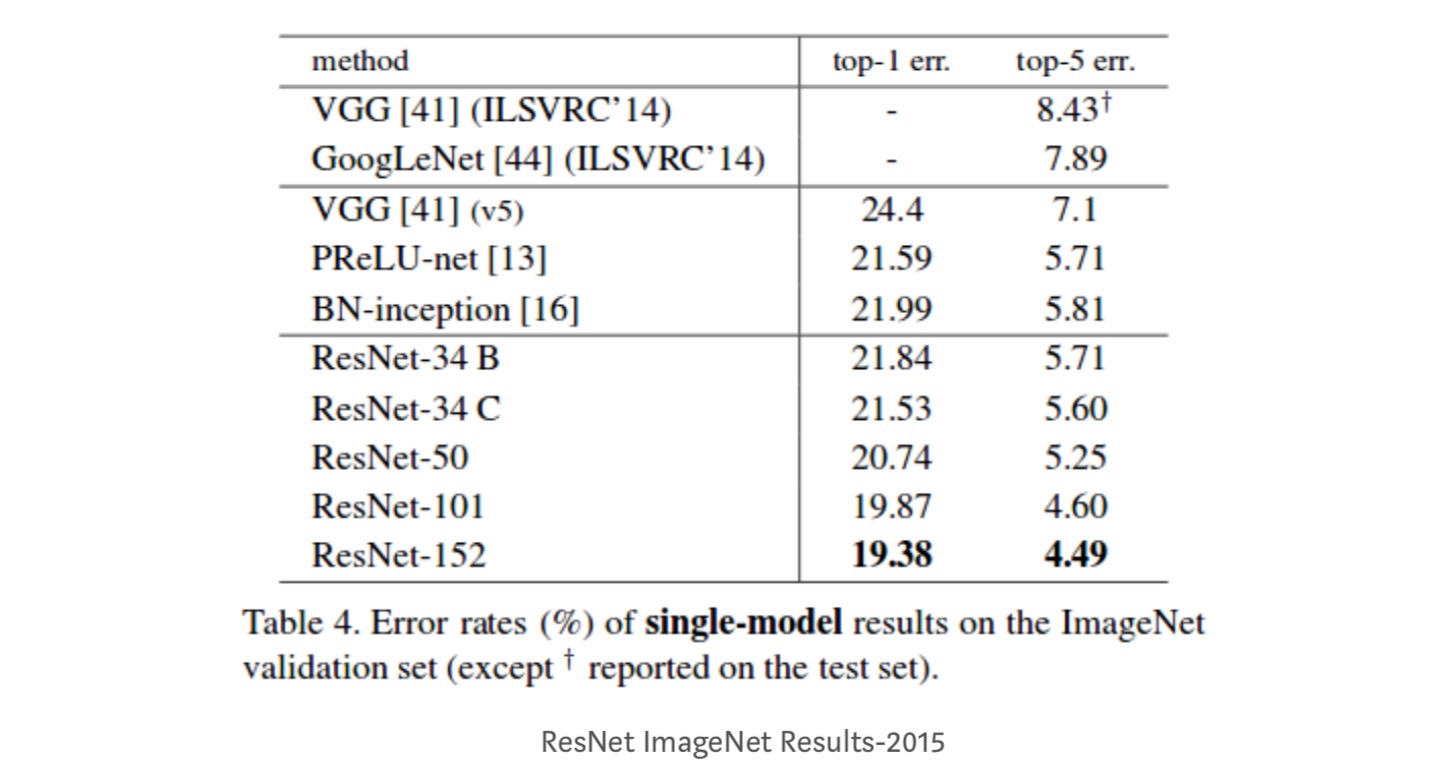
- a ResNet-34 top-5 validációs hibát ért el 5,71%-kal jobb, mint a BN-inception és a VGG. ResNet-152 eléri a top-5 Érvényesítési hiba 4,49%. 6 különböző mélységű modell együttese a top-5 érvényesítési hibát 3,57% – kal éri el. 1. hely elnyerése az ILSVRC-2015 – ben
Identitásleképezések mély maradék hálózatokban
Ez a tanulmány elméleti megértést nyújt arról, hogy miért nincs jelen eltűnő gradiens probléma a maradék hálózatokban, valamint a kapcsolatok kihagyása (a kapcsolatok kihagyása a bemenetet jelenti vagy ) azáltal, hogy az Identitásleképezést (x) különböző funkciókkal helyettesíti.
Bevezetés
a mély maradék hálózatok sok halmozott “maradék egységből”állnak. Minden egység általános formában fejezhető ki:
ahol és amelyek az egység bemenete és kimenete, és maradékfüggvény. Az utolsó papír, egy identitás leképezés és egy ReLU függvény.
a Resnetek központi gondolata az additív maradék funkció megtanulása a vonatkozásában , kulcsfontosságú választás az identitásleképezés használatával . Ez egy identity skip kapcsolat (“parancsikon”) csatolásával valósul meg.
ebben a cikkben elemezzük a mély maradék hálózatokat azáltal, hogy egy “közvetlen” útvonal létrehozására összpontosítunk az információ terjesztésére — nem csak a maradék egységen belül, hanem az egész hálózaton keresztül. Levezetéseink azt mutatják, hogy ha mindkettő identitás-leképezés, akkor a jel közvetlenül továbbítható egyik egységről bármely más egységre, mind előre, mind hátra haladva. Kísérleteink empirikusan azt mutatják, hogy a képzés általában könnyebbé válik, ha az architektúra közelebb áll a fenti két feltételhez.
a kapcsolatok kihagyásának szerepének megértéséhez elemezzük és összehasonlítjuk a különböző típusokat . Megállapítottuk, hogy a legutóbbi tanulmányban kiválasztott Azonosság-leképezés az összes vizsgált változat közül a leggyorsabb hibacsökkentést és a legalacsonyabb edzésveszteséget éri el, míg a méretezés , a kapuzás és az 1 6.számú konvolúció kihagyása magasabb edzésveszteséghez és hibához vezet. Ezek a kísérletek azt sugallják, hogy a” tiszta ” információs út megtartása hasznos az optimalizálás megkönnyítéséhez.
az identitásleképezés elkészítéséhez az aktiválási függvényeket (ReLU és BN) a súlyrétegek “előaktiválásának” tekintjük , ellentétben az “utóaktiválás”hagyományos bölcsességével. Ez a nézőpont egy új maradék egység kialakításához vezet, amelyet a következő ábra mutat. Ezen egység alapján versenyképes eredményeket mutatunk be a CIFAR-10/100-on egy 1001 rétegű Resnettel, amelyet sokkal könnyebb kiképezni és általánosítani, mint az eredeti ResNet. Továbbá az ImageNet javított eredményeiről számolunk be egy 200 rétegű ResNet használatával, amelynél az utolsó papír megfelelője túlfit. Ezek az eredmények azt sugallják, hogy sok hely van a hálózati mélység dimenziójának kiaknázására, amely a modern mély tanulás sikerének kulcsa.
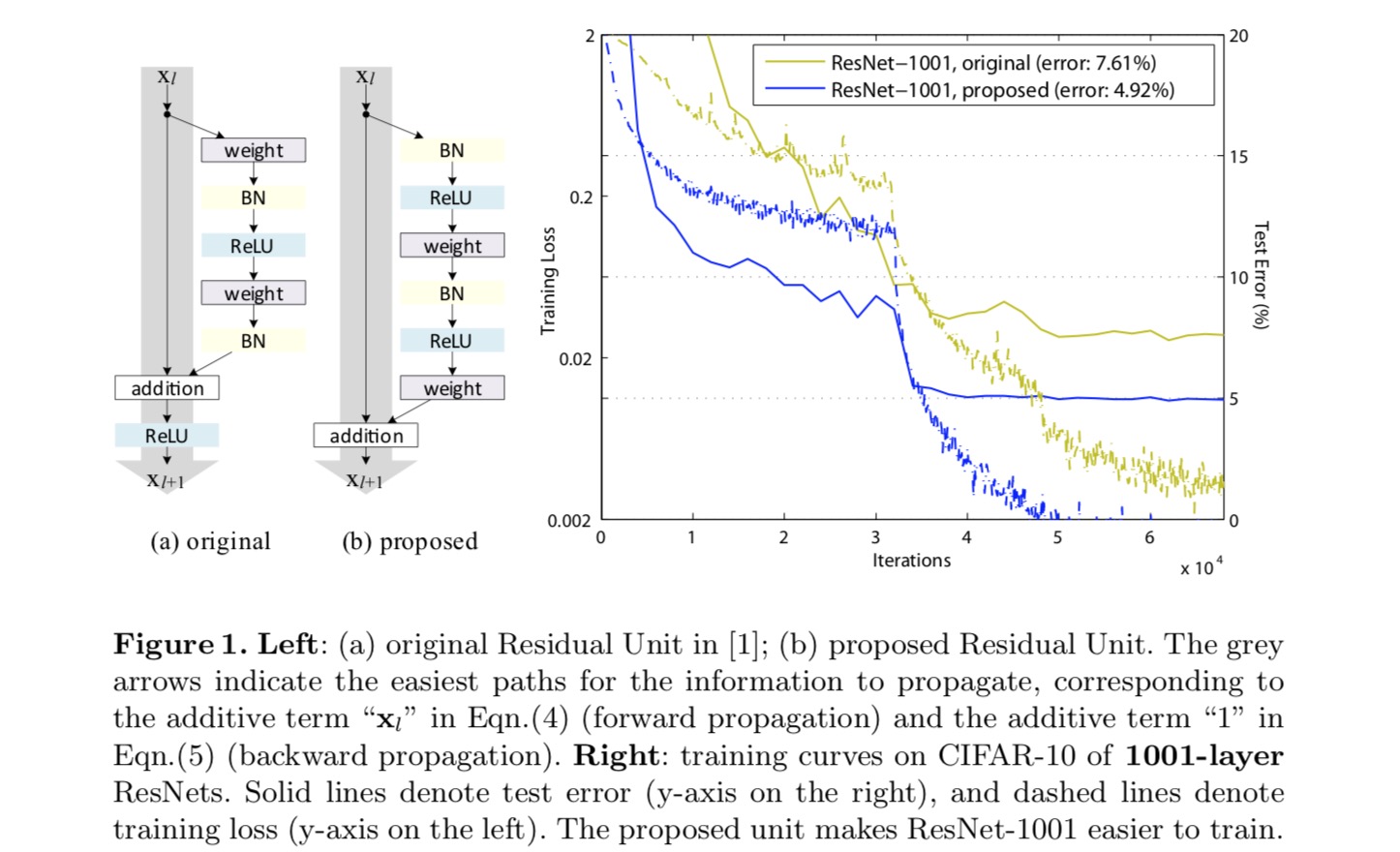
mély maradék hálózatok elemzése
az utolsó cikkben kifejlesztett Resnetek modularizált architektúrák, amelyek ugyanolyan összekötő alakú építőelemeket raknak össze. Ebben a cikkben ezeket a blokkokat “maradék egységeknek”nevezzük. Az utolsó papír eredeti maradék egysége a következő számítást hajtja végre:
itt látható a-th maradék egység bemeneti funkciója. a-th maradék egységhez társított súlyok (és torzítások) halmaza, és a maradék egység rétegeinek száma ( 2 vagy 3 az utolsó papírban). a maradék funkciót jelöli, e.g., egy köteg két 3 db 3 konvolúciós rétegből az utolsó papírban. A funkció az elemenkénti összeadás utáni művelet, az utolsó papír pedig ReLU. A funkció identitásleképezésként van beállítva:.
Ha ez is egy identitásleképezés:, megkaphatjuk:
rekurzív módon megkapjuk:
bármely mélyebb és sekélyebb egység esetében . Ez az egyenlet néhány széptulajdonságait. (1) bármely mélyebb egység jellemzője bármely sekélyebb egység jellemzőjeként ábrázolható , plusz egy maradék funkció formájában, jelezve, hogy a modell maradék módon van bármely egység között . (2) bármely mély egység jellemzője az összes előző maradék funkció kimenetének összegzése (plusz). Ez ellentétben áll a “sima hálózattal”, ahol a jellemző mátrix-vektor termékek sorozata, mondjuk (figyelmen kívül hagyva a bn-t és a ReLU-t).
a fenti egyenlet szép visszafelé terjedési tulajdonságokhoz is vezet. A veszteségfüggvényt úgy jelöljük , mint a backpropagation láncszabályából:
a fenti egyenlet azt jelzi, hogy a gradiens két additív kifejezésre bontható: olyan kifejezés, amely közvetlenül terjeszti az információkat anélkül, hogy bármilyen súlyrétegre vonatkozna, egy másik kifejezés pedig a súlyrétegeken keresztül terjed. Az additív kifejezés biztosítja, hogy az információ közvetlenül visszakerüljön bármely sekélyebb egységbe l. a fenti egyenlet azt is sugallja, hogy valószínűtlen, hogy a gradiens törlődik egy mini-tételnél, mert általában a kifejezés nem mindig lehet -1 a mini-tétel összes mintájára. Ez azt jelenti, hogy egy réteg gradiense akkor sem tűnik el, ha a súlyok önkényesen kicsiek.
a fenti két egyenlet azt sugallja, hogy a jel közvetlenül továbbítható bármely egységről a másikra, mind előre, mind hátra. Az első fenti két egyenlet alapja két identitásleképezés: (1) az identitás kihagyása kapcsolat , és (2) az a feltétel, amely egy identitásleképezés.
az identitás fontossága ugrás kapcsolatok
Vegyünk egy egyszerű módosítást, , az identitás parancsikonjának megtörésére:
hol van egy moduláló skalár (az egyszerűség kedvéért még mindig feltételezzük, hogy az identitás). Ezt a megfogalmazást rekurzívan alkalmazva a fentihez hasonló egyenletet kapunk:
ahol a jelölés elnyeli a skalárokat a maradék funkciókba. Hasonlóképpen, a következő formájú backpropagációnk van:
az előző egyenlettől eltérően ebben az egyenletben az első additív kifejezést egy tényező modulálja . Egy rendkívül mély hálózat (nagy), ha mindenki számára, ez a tényező lehet exponenciálisan nagy; ha mindenki számára , ez a tényező lehet exponenciálisan kicsi és eltűnik, ami blokkolja a backpropagated jelet a parancsikonból, és arra kényszeríti, hogy átfolyjon a súlyrétegeken. Ez optimalizálási nehézségeket eredményez, amint azt kísérletek mutatják.
a fenti elemzésben az eredeti identity skip kapcsolat helyébe egy egyszerű méretezés lép . Ha az átugrási kapcsolat bonyolultabb transzformációkat jelent (mint például a kapuzás és az 1 db 1 konvolúció), akkor a fenti egyenletben az első kifejezés lesz hol van a deriváltja . Ez a termék akadályozhatja az információ terjesztését és akadályozhatja a képzési eljárást, amint azt a következő kísérletek is bizonyítják.
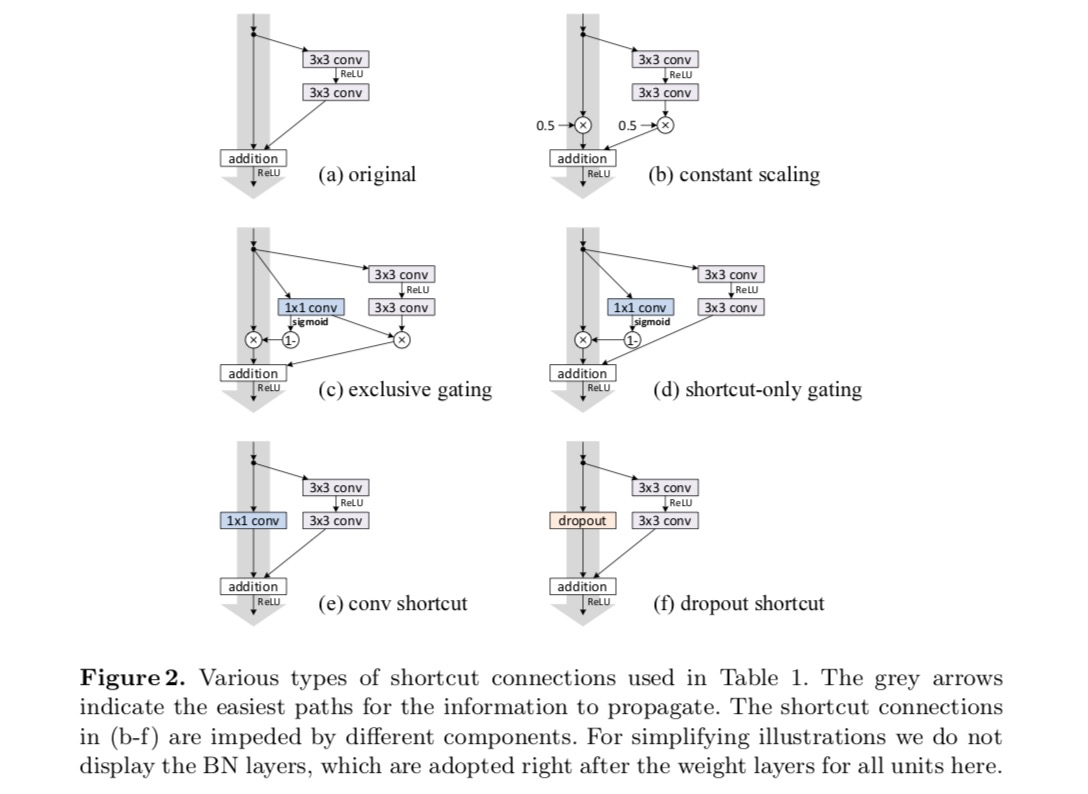
kísérletek Ugrás kapcsolatok
kísérletezünk a 110 rétegű ResNet a CIFAR-10. Ez a rendkívül mély ResNet-110 54 kétrétegű maradék egységgel rendelkezik (amely 3 db 3 konvolúciós rétegből áll), és kihívást jelent az optimalizálás szempontjából. Különböző típusú kihagyási kapcsolatokat kísérleteznek. Lásd a következő ábrát:
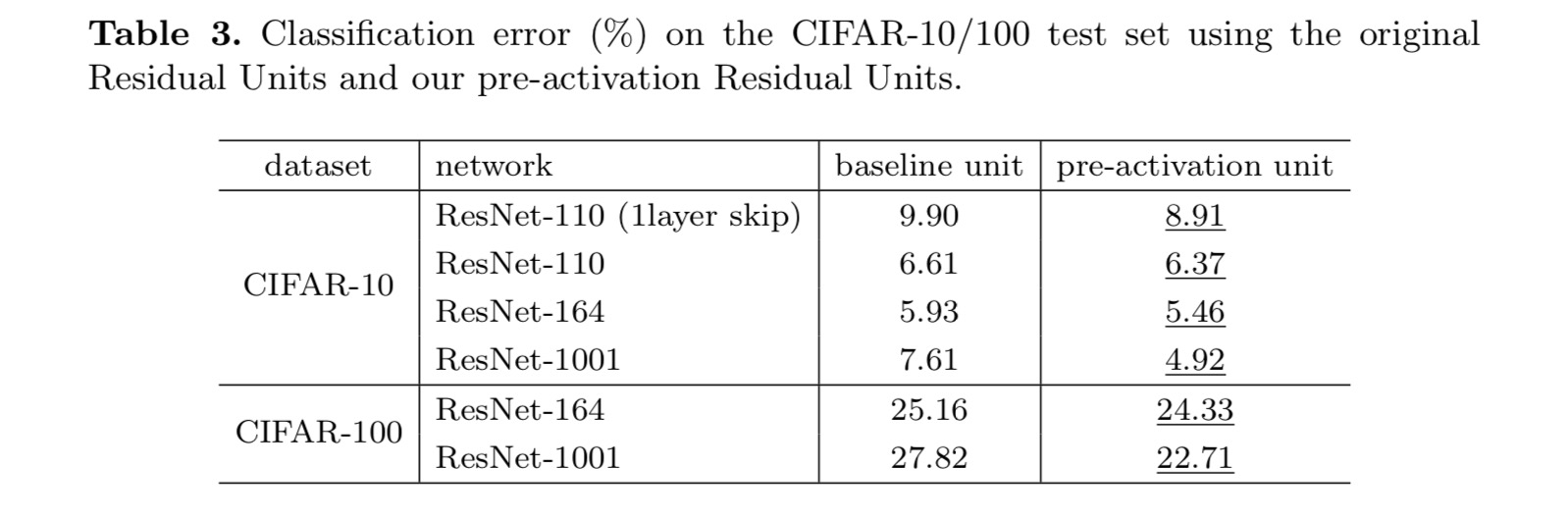
az osztályozási eredmények a következő táblázatban láthatók:
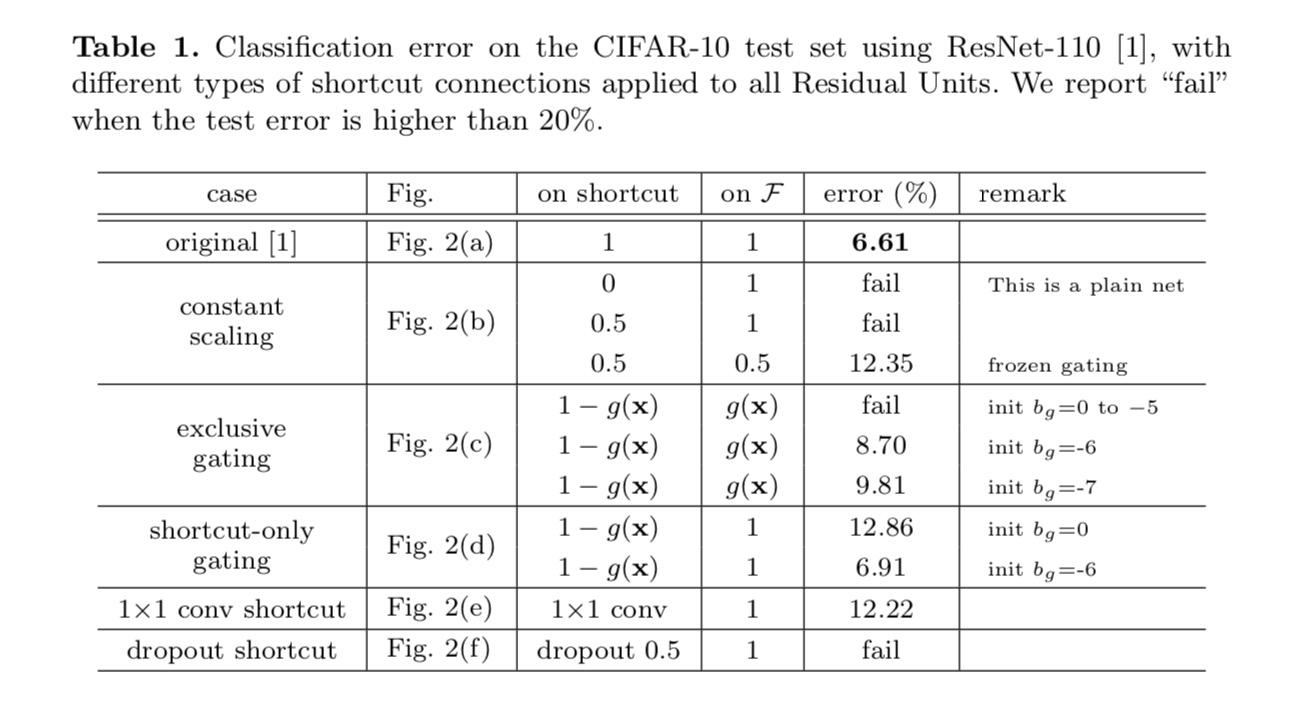
amint azt a fenti ábrán látható szürke nyilak jelzik, a parancsikonok a legközvetlenebb útvonalak az információ terjesztéséhez. A parancsikonokon végzett multiplikatív manipulációk (méretezés, kapuzás, 1! 1 konvolúció és lemorzsolódás) gátolhatják az információ terjedését és optimalizálási problémákhoz vezethetnek.
figyelemre méltó, hogy a kapuzási és az 1 ons 1 konvolúciós parancsikonok több paramétert vezetnek be, és erősebb reprezentációs képességekkel kell rendelkezniük, mint az identitáshivatkozások. Valójában a csak parancsikont tartalmazó kapuzás és az 1! 6. számú konvolúció lefedi az identitáshivatkozások megoldási terét (azaz optimalizálhatók identitáshivatkozásként). Képzési hibájuk azonban magasabb, mint az identitás parancsikonoké, ami azt jelzi, hogy ezeknek a modelleknek a romlását a reprezentációs képességek helyett az optimalizálási problémák okozzák.
aktiválási függvények használata
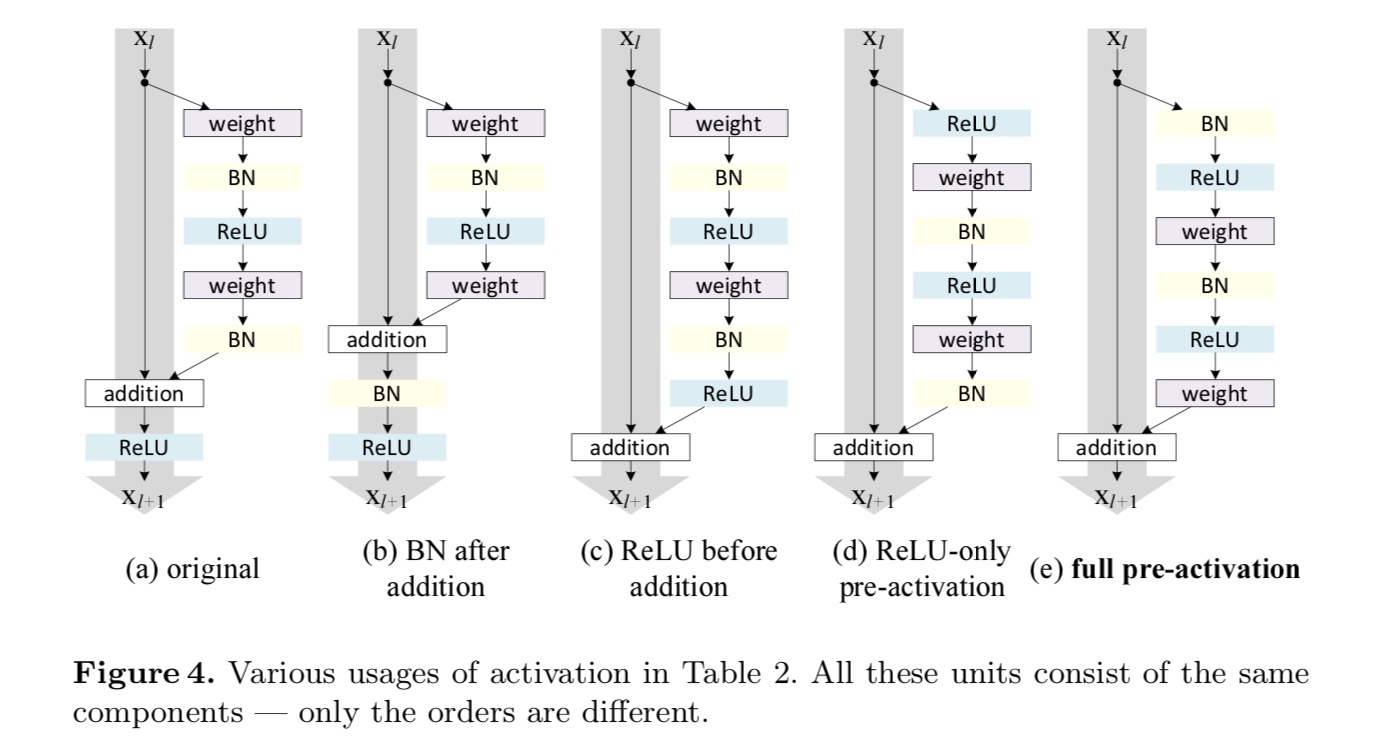
a fenti szakaszban végzett kísérletek azt feltételezik, hogy az addíció utáni aktiválás az identitásleképezés. De a fenti kísérletek ReLU tervezett az első papír. Ezután megvizsgáljuk a hatását .
identitásleképezést szeretnénk készíteni, ami az aktiválási függvények újrarendezésével történik (ReLU és / vagy BN, kötegelt normalizálás). A következő ábrán az utolsó papír eredeti maradék egységének alakja az ábrán látható. A 4 (a) – BN-t minden súlyréteg után használjuk, a ReLU-t pedig BN után fogadjuk el, azzal a különbséggel, hogy a maradék egységben az utolsó ReLU elemenkénti összeadás után van (=ReLU). Fig. 4 (b-e) mutassa be az általunk vizsgált alternatívákat.
kísérletek az Aktiválásra
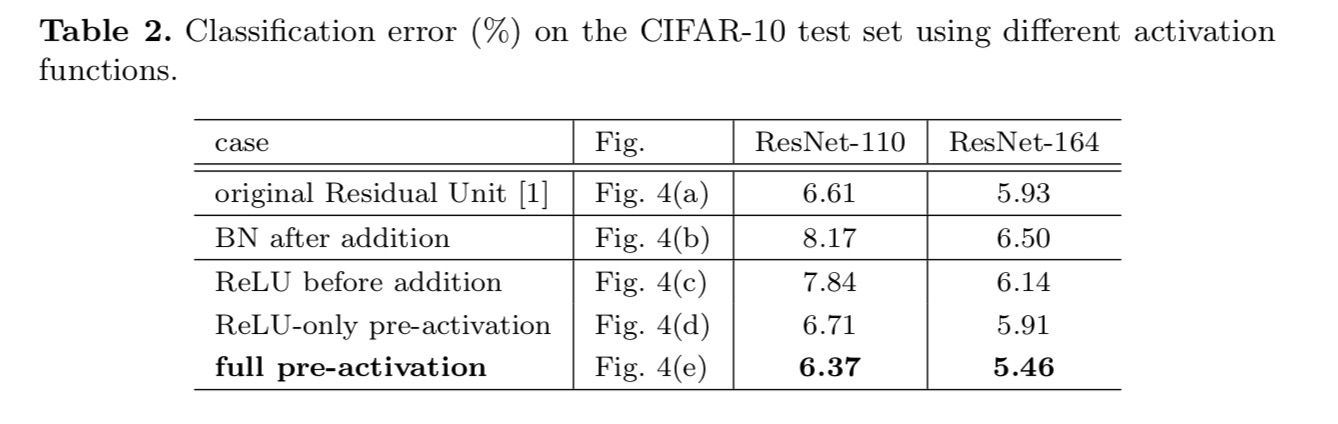
ebben a részben a ResNet-110 és egy 164 rétegű szűk keresztmetszeti architektúrával kísérletezünk (ResNet-164-ként jelölve). A szűk keresztmetszet maradék egysége egy 1 db 1 rétegből áll a dimenzió csökkentésére, egy 3 db 3 rétegből és egy 1 db 1 rétegből a dimenzió helyreállítására. Az utolsó cikkben leírtak szerint számítási bonyolultsága hasonló a kettőhöz-3 6. számú 6. számú maradék egység.
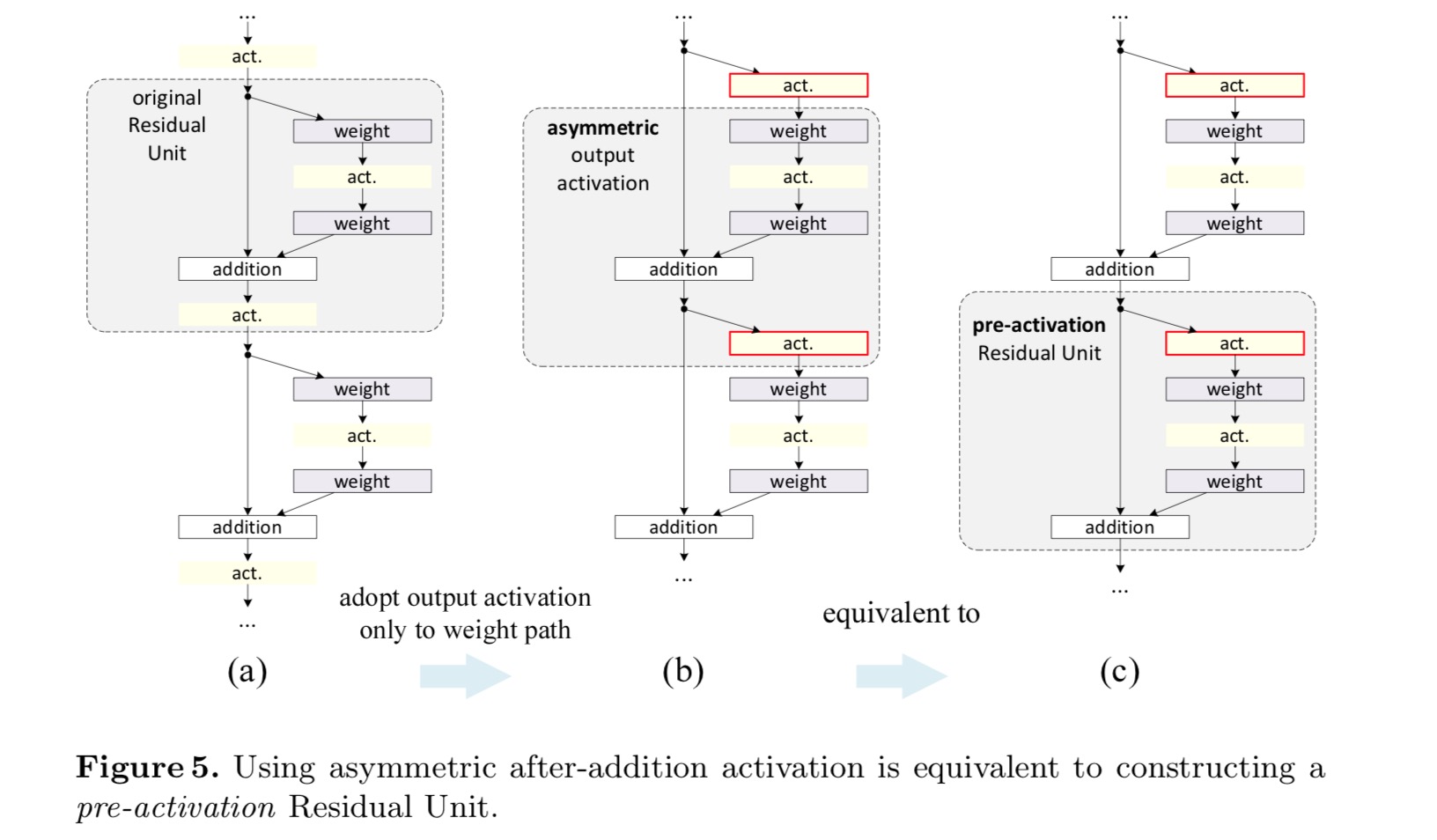
poszt-aktiválás vagy pre-aktiválás?
az eredeti tervben az aktiválás a következő maradék egység mindkét útvonalát érinti: . Ezután egy aszimmetrikus formát fejlesztünk ki, ahol az aktiválás csak az utat érinti: , bármelyik számára . A jelölések átnevezésével a következő formát kapjuk:
ehhez az új maradék egységhez, mint a fenti egyenletben, az új kiegészítés utáni aktiválás identitásleképezéssé válik. Ez a kialakítás azt jelenti, hogy ha egy új addíció utáni aktiválást aszimmetrikusan alkalmaznak, akkor az egyenértékű a következő maradék egység előaktiválásaként történő átdolgozással. Ezt a következő ábra szemlélteti:
Az aktiválás utáni/előaktiválás közötti különbséget az elemenkénti kiegészítés jelenléte okozza. Egy N rétegű sima hálózat esetében vannak N − 1 aktivációk (BN / ReLU), és nem számít, hogy poszt – vagy pre-aktivációknak tekintjük őket. De az elágazó rétegek egyesítése mellett az aktiválás helyzete fontos. Az aktiválás különböző felhasználási módjait a 4.ábra mutatja.
két ilyen tervvel kísérletezünk: (1) ReLU-csak pre-aktiválás és (2) teljes pre-aktiválás, ahol BN és ReLU egyaránt elfogadott előtt súly réteg. Valahogy meglepő módon, amikor a bn-t és a ReLU-t egyaránt használják előaktiválásként, az eredményeket egészséges margók javítják
azt találjuk, hogy az előaktiválás hatása kettős. Először is, az optimalizálás tovább enyhül (összehasonlítva az alapszintű ResNet-tel), mert f egy identitásleképezés. Másodszor, a BN használata előaktiválásként javítja a modellek szabályozását.
következtetés
Ez a tanulmány a mély maradék hálózatok csatlakozási mechanizmusai mögötti terjedési formulákat vizsgálja. Levezetéseink azt sugallják, hogy az identitás rövidre vágott kapcsolatai és az identitás addíció utáni aktiválása elengedhetetlenek az információ terjedésének gördülékenyebbé tételéhez. Az ablációs kísérletek olyan phenom-ena-t mutatnak, amelyek összhangban vannak a levezetéseinkkel. 1000 rétegű mélyhálózatokat is bemutatunk, amelyek könnyen betaníthatók és jobb pontosságot érhetnek el.
aggregált maradék transzformáció a mély neurális hálózatokhoz
Bevezetés
a vizuális felismeréssel kapcsolatos kutatások átmeneten mennek keresztül a “funkciómérnöki” – ről a “hálózati mérnöki” – re. Az emberi erőfeszítések A jobb hálózati architektúrák tervezésére irányultak a tanulási reprezentációk számára.
az architektúrák tervezése egyre nehezebbé válik a hiper-paraméterek növekvő számával, különösen akkor, ha sok réteg van. A VGG-hálók egyszerű, de hatékony stratégiát mutatnak a nagyon mély hálózatok felépítésére: azonos alakú építőelemek egymásra rakása. Ezt a stratégiát olyan Resnetek öröklik, amelyek ugyanazon topológia moduljait rakják össze. Ez az egyszerű szabály csökkenti a hiperparaméterek szabad választását, és a mélység a neurális hálózatok alapvető dimenziójaként jelenik meg. Sőt, azzal érvelünk, hogy ennek a szabálynak az egyszerűsége csökkentheti annak kockázatát, hogy a hiperparamétereket egy adott adatkészlethez túlzottan adaptálják. A VGG-hálók és Resnetek robusztusságát különböző vizuális felismerési feladatok, valamint a beszédet és a nyelvet érintő nem vizuális feladatok bizonyították.
a VGG-netekkel ellentétben az Inception modellek családja bebizonyította, hogy a gondosan megtervezett topológiák alacsony elméleti bonyolultsággal képesek meggyőző pontosságot elérni. Az Inception modellek idővel fejlődtek, de fontos közös tulajdonság a split-transform-merge stratégia. Az Inception modulban a bemenet néhány alacsonyabb dimenziós beágyazásra oszlik (1 db 6-1 konvolúcióval), amelyeket speciális szűrők (3 db 3, 5 db 5 stb.) átalakítanak.), és összefűzéssel egyesítették. Az Inception modulok split-transform-merge viselkedése várhatóan megközelíti a nagy és sűrű rétegek reprezentációs erejét, de lényegesen alacsonyabb számítási bonyolultsággal.
a jó pontosság ellenére az Inception modellek megvalósítását számos bonyolító tényező kísérte. Bár ezeknek az összetevőknek a gondos kombinációja kiváló neurális hálózati recepteket eredményez, általában nem világos, hogyan lehet az Inception architektúrákat új adatkészletekhez/feladatokhoz igazítani, különösen akkor, ha sok tényezőt és hiperparamétert kell megtervezni.
ebben a cikkben egy egyszerű architektúrát mutatunk be, amely a VGG/ResNets ismétlődő rétegek stratégiáját alkalmazza, miközben a split-transform-merge stratégiát könnyen, bővíthető módon használja ki. A hálózatunk egy modulja egy sor transzformációt hajt végre, mindegyik alacsony dimenziós Beágyazással, amelynek kimeneteit összegzéssel összesítik. Ennek az ötletnek az egyszerű megvalósítását követjük-az összesítendő transzformációk mind ugyanabból a topológiából származnak. Ez a kialakítás lehetővé teszi számunkra, hogy bármilyen nagyszámú átalakításra kiterjedjünk speciális tervek nélkül.
empirikusan bizonyítjuk, hogy összesített transzformációink felülmúlják az eredeti ResNet modult, még a számítási komplexitás és a modellméret fenntartásának korlátozott feltételei mellett is. Hangsúlyozzuk, hogy bár viszonylag könnyű növelni a pontosságot a kapacitás növelésével (mélyebbre vagy szélesebbé téve), az irodalomban ritkák azok a módszerek, amelyek növelik a pontosságot, miközben fenntartják (vagy csökkentik) a komplexitást.
módszerünk azt jelzi, hogy a kardinalitás (a transzformációk halmazának mérete) egy konkrét, mérhető dimenzió, amely központi jelentőségű, a szélesség és a mélység dimenziói mellett. A kísérletek azt mutatják, hogy a növekvő kardinalitás hatékonyabb módja a pontosság megszerzésének, mint a mélyebb vagy szélesebb, különösen akkor, ha a mélység és a szélesség csökkenő hozamot eredményez a meglévő modelleknél.
a ResNeXt nevű neurális hálózataink felülmúlják a ResNet-101/152, ResNet-200, Inception-v3 és Inception-ResNet-v2 szabványokat az ImageNet osztályozási adatbázisában. Különösen egy 101 rétegű ResNeXt képes jobb pontosságot elérni, mint a ResNet-200, de csak 50% – os komplexitással rendelkezik. Sőt, a ResNeXt lényegesen egyszerűbb mintákat mutat, mint az összes Inception modell.
módszer
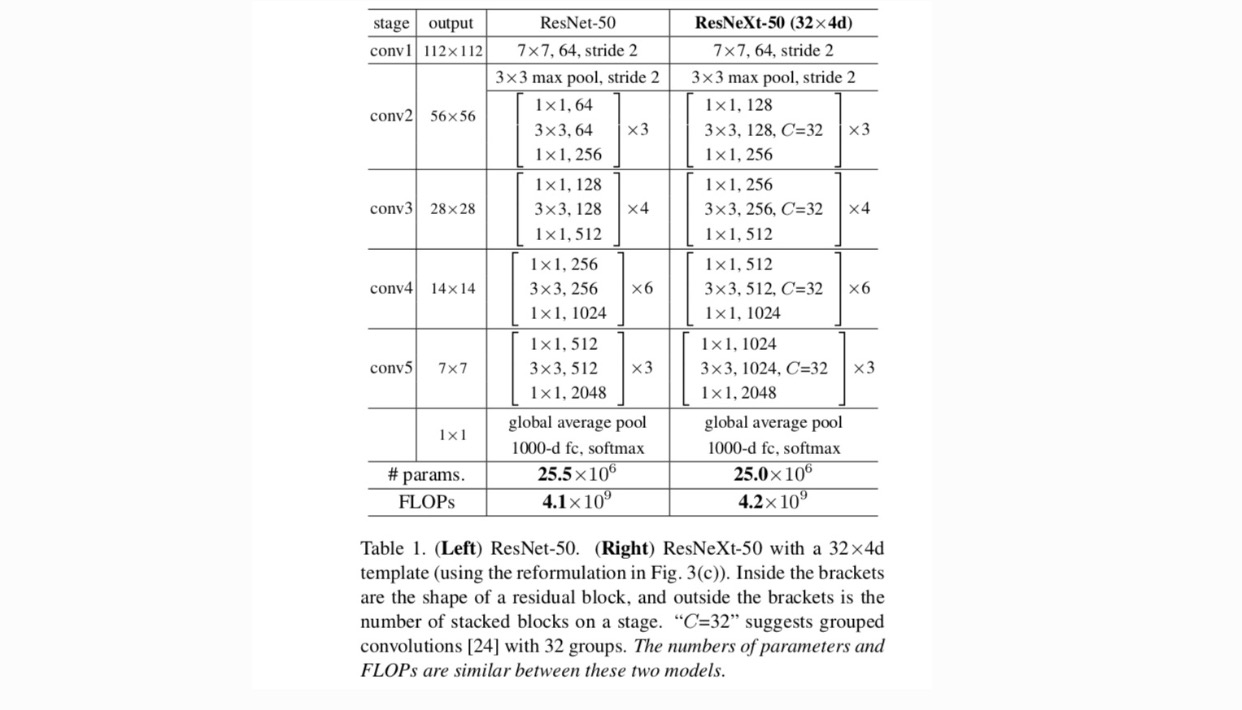
a VGG/ResNets után nagyon modularizált kialakítást alkalmazunk. Hálózatunk egy halom maradék blokkból áll. Ezeknek a blokkoknak ugyanaz a topológiája, és két, a VGG/ResNets által inspirált egyszerű szabály vonatkozik rájuk: (1) ha azonos méretű térbeli térképeket készítenek, a blokkok ugyanazokkal a hiperparaméterekkel rendelkeznek (szélesség és szűrőméret), és (2) minden alkalommal, amikor a térbeli térképet 2-szeresére csökkentik, a blokkok szélességét 2-szeres szorzóval megszorozzuk. A második szabály biztosítja, hogy a számítási komplexitás a flopok (lebegőpontos műveletek, a szorzás-összeadások #-ban) szempontjából nagyjából azonos minden blokk esetében.
ezzel a két szabállyal csak egy sablonmodult kell megterveznünk, és a hálózat összes modulja ennek megfelelően meghatározható. Tehát ez a két szabály nagymértékben szűkíti a tervezési teret, és lehetővé teszi számunkra, hogy néhány kulcsfontosságú tényezőre összpontosítsunk. Az e szabályok által létrehozott hálózatokat az 1. táblázat tartalmazza.
a mesterséges neurális hálózatok legegyszerűbb neuronjai belső szorzatot (súlyozott összeget) hajtanak végre, amely a teljesen összekapcsolt és konvolúciós rétegek elemi transzformációja.
a fenti művelet átdolgozható a felosztás, átalakítás és aggregálás kombinációjaként. (1): hasítás: a vektor alacsony dimenziós beágyazásként van szeletelve, és a fentiekben egydimenziós altér (2) transzformáció: az alacsony dimenziós ábrázolás átalakul, a fentiekben pedig egyszerűen méretezhető: (3) Aggregálás: az összes beágyazásban lévő transzformációkat összesíti .
tekintettel egy egyszerű neuron fenti elemzésére, úgy gondoljuk, hogy az elemi transzformációt (w_i, x_i) egy általánosabb funkcióval helyettesítjük, amely önmagában is hálózat lehet. Formálisan összesített transzformációkat mutatunk be:
ahol tetszőleges függvény lehet. Egy egyszerű neuronhoz hasonlóan egy (opcionálisan alacsony dimenziós) beágyazódásba kell vetülnie, majd átalakítania kell.
ezt nevezzük kardinalitásnak. az in-hez hasonló helyzetben van , de nem kell egyenlőnek lennie, és tetszőleges szám lehet. Kísérletekkel megmutatjuk, hogy a kardinalitás alapvető dimenzió, és hatékonyabb lehet, mint a szélesség és a mélység dimenziói.
ebben a cikkben a transzformációs függvények tervezésének egyszerű módját vesszük figyelembe: minden topológiának ugyanaz a topológiája. Ez kiterjeszti az azonos alakú rétegek ismétlésének VGG-stílusú stratégiáját. Az egyéni átalakítást az ábrán bemutatott szűk keresztmetszet alakú architektúrának állítottuk be. 1 (jobbra). Ebben az esetben az első 1 db 1 réteg mindegyikben alacsony dimenziós beágyazást eredményez.
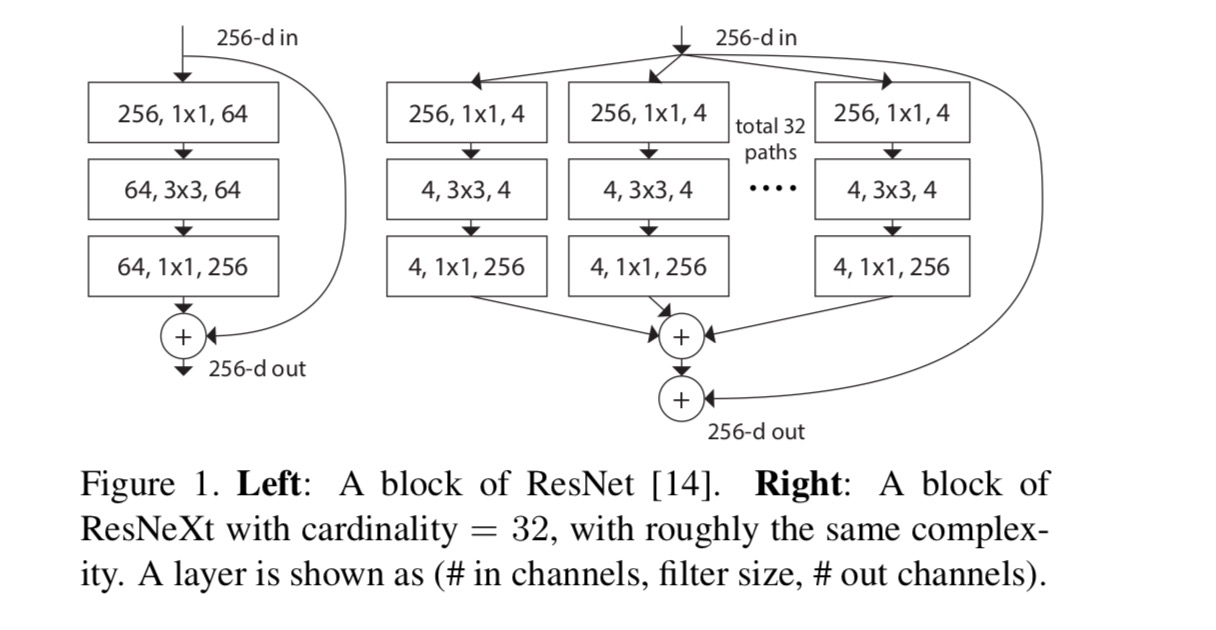
az utolsó egyenlet összesített transzformációja maradék függvényként szolgál:
hol van a kimenet.
a ResNeXt és az Inception-ResNet/Grouped-Convolutions közötti kapcsolatokat a következő ábra mutatja:
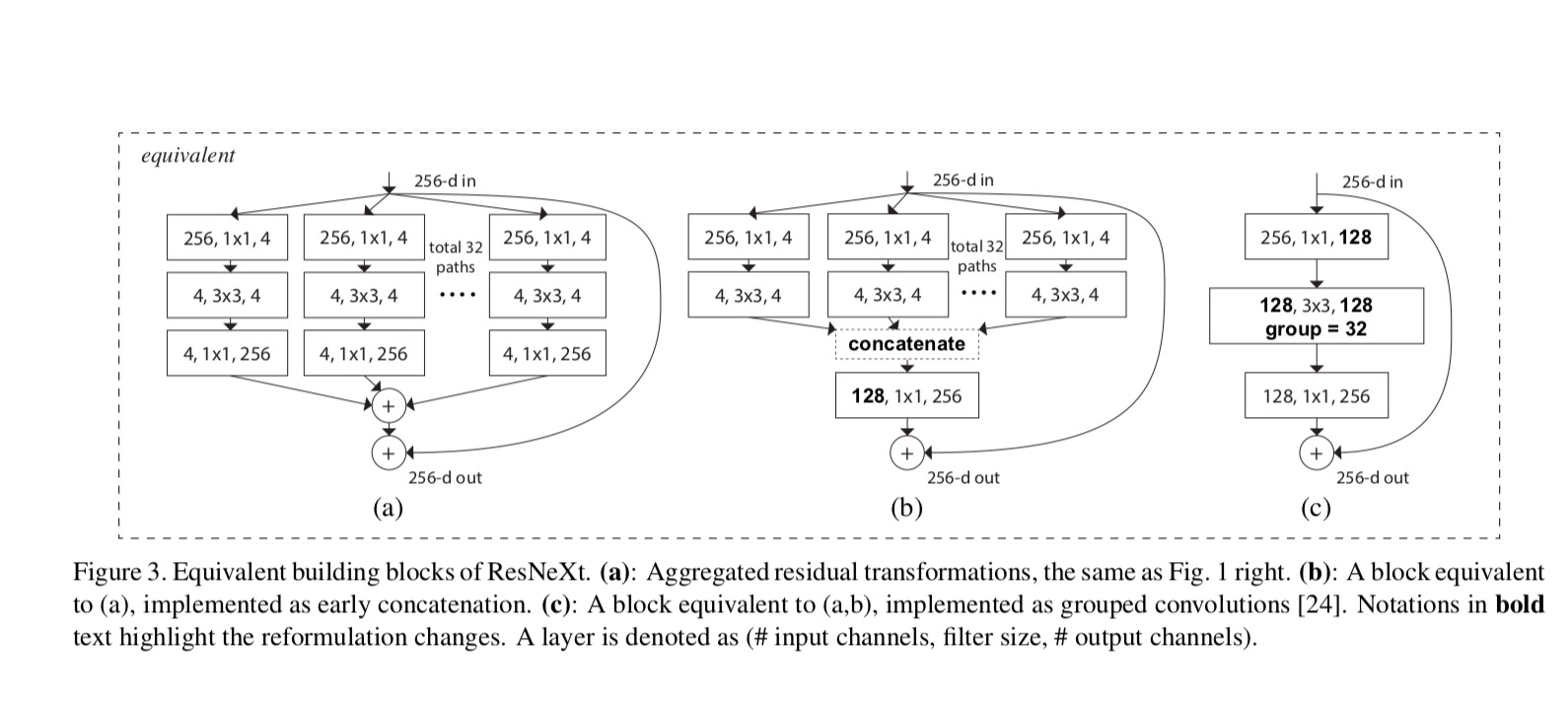
amikor a különböző kardinalitásokat értékeljük, miközben megőrizzük a komplexitást, minimalizáljuk a többi hiper-paraméter módosítását. 4-d az 1. ábrán (jobbra)), mert elkülöníthető a blokk bemenetétől és kimenetétől. Ez a stratégia nem változtat más hiperparamétereken (a blokkok mélysége vagy bemeneti/kimeneti szélessége), ezért hasznos számunkra, hogy a kardinalitás hatására összpontosítsunk.
ábrán. 1 (balra), az eredeti ResNet szűk keresztmetszet blokk paraméterekkel és arányos flopokkal rendelkezik(ugyanazon a jellemző térképen). A szűk keresztmetszet szélessége, a sablon ábra. 1 (jobbra): paraméterek és arányos flopok. Mikor és ezt a számot . Az alábbi táblázat a kardinalitás és a szűk keresztmetszet közötti kapcsolatot mutatja be .

kísérletek
Kardinalitás vs.Szélesség. Először a kardinalitás és a szűk keresztmetszet közötti kompromisszumot értékeljük a 2.táblázatban felsorolt, megőrzött összetettség alapján. A 3. táblázat mutatja az eredményeket. Összehasonlítva ResNet-50, a 32 6d 6d ResNeXt-50 validációs hibája 22,2%, ami 1,7% – kal alacsonyabb, mint a ResNet alapvonala 23,9%. A kardinalitás 1-ről 32-re növekszik, miközben a komplexitás megmarad, a hibaarány folyamatosan csökken. Továbbá a 32 6d 6d ResNeXt szintén sokkal alacsonyabb képzési hibával rendelkezik, mint a ResNet countetpart, ami arra utal, hogy a nyereség nem a szabályozásból, hanem az erősebb reprezentációkból származik.
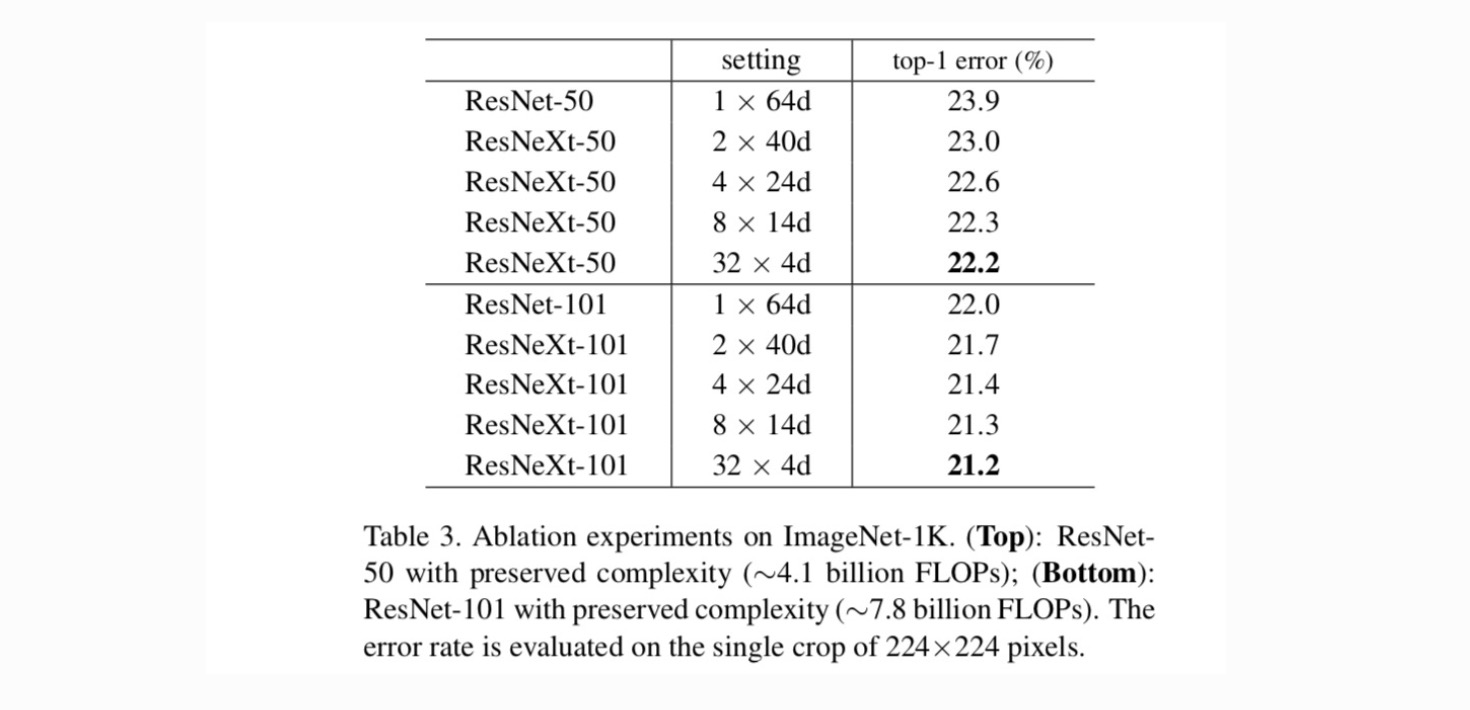
növekvő Kardinalitás vs.mélyebb/szélesebb.
ezután a növekvő komplexitást vizsgáljuk a C kardinalitás növelésével vagy a mélység vagy szélesség növelésével. Összehasonlítjuk a következő változatokat (1), amelyek 200 rétegre mélyülnek. Elfogadjuk a ResNet-200-at. (2) szélesebb lesz a szűk keresztmetszet szélességének növelésével. (3) a cardinalitás növelése a C.
megkétszerezésével a 4.táblázat azt mutatja, hogy a komplexitás 2 db-tal történő növelése következetesen csökkenti a hibát a ResNet-101 kiindulási értékhez képest (22,0%). De a javulás kicsi, ha mélyebbre megy (ResNet-200, 0,3%-kal) vagy szélesebb (szélesebb ResNet-101, 0,7% – kal). Éppen ellenkezőleg, a növekvő kardinalitás C sokkal jobb eredményeket mutat, mint mélyebbre vagy szélesebbre.
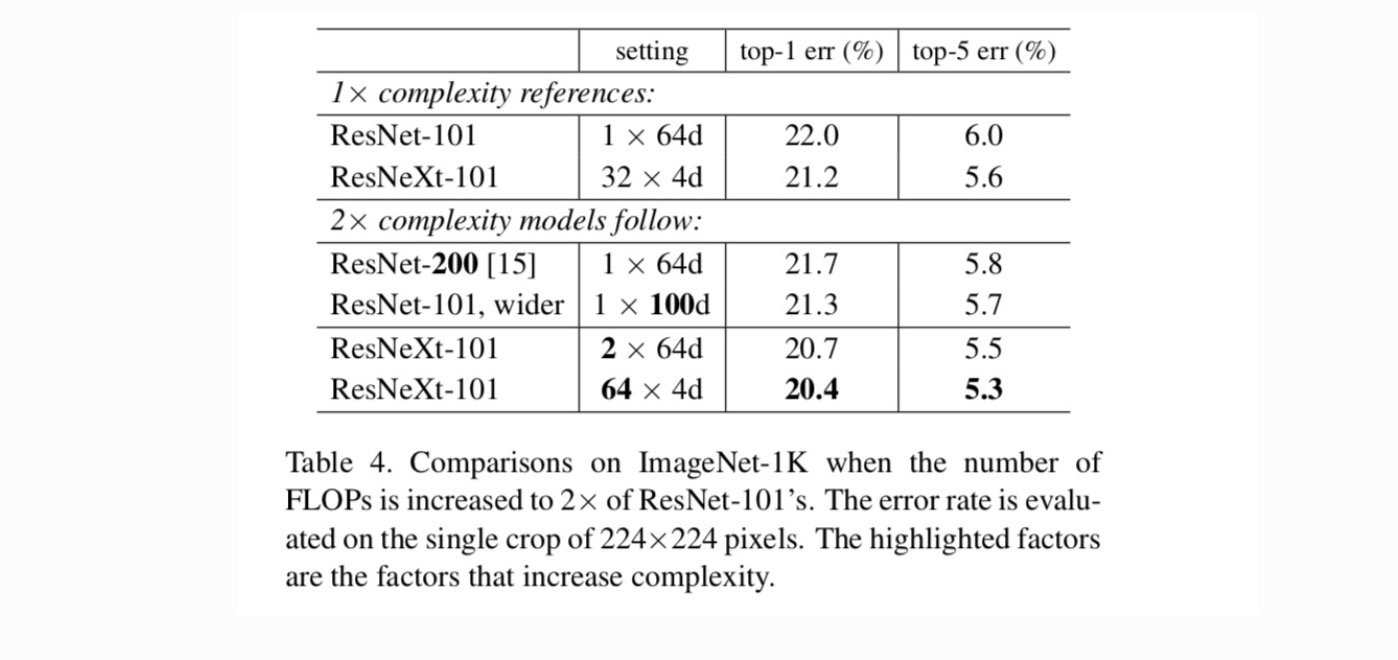
összehasonlítás a legkorszerűbb eredményekkel. Az 5.táblázat az IMAGEnet validációs készleten végzett egyterű vizsgálatok további eredményeit mutatja. Eredményeink kedvezően hasonlítanak a ResNet, az Inception-v3/v4 és az Inception-ResNet-v2-hez, elérve az egytermésű top-5 hibaarányt 4,4% – kal. Ezen túlmenően az architektúra kialakítása sokkal egyszerűbb, mint az összes Inception modell, és lényegesen kevesebb hiperparamétert igényel kézzel.
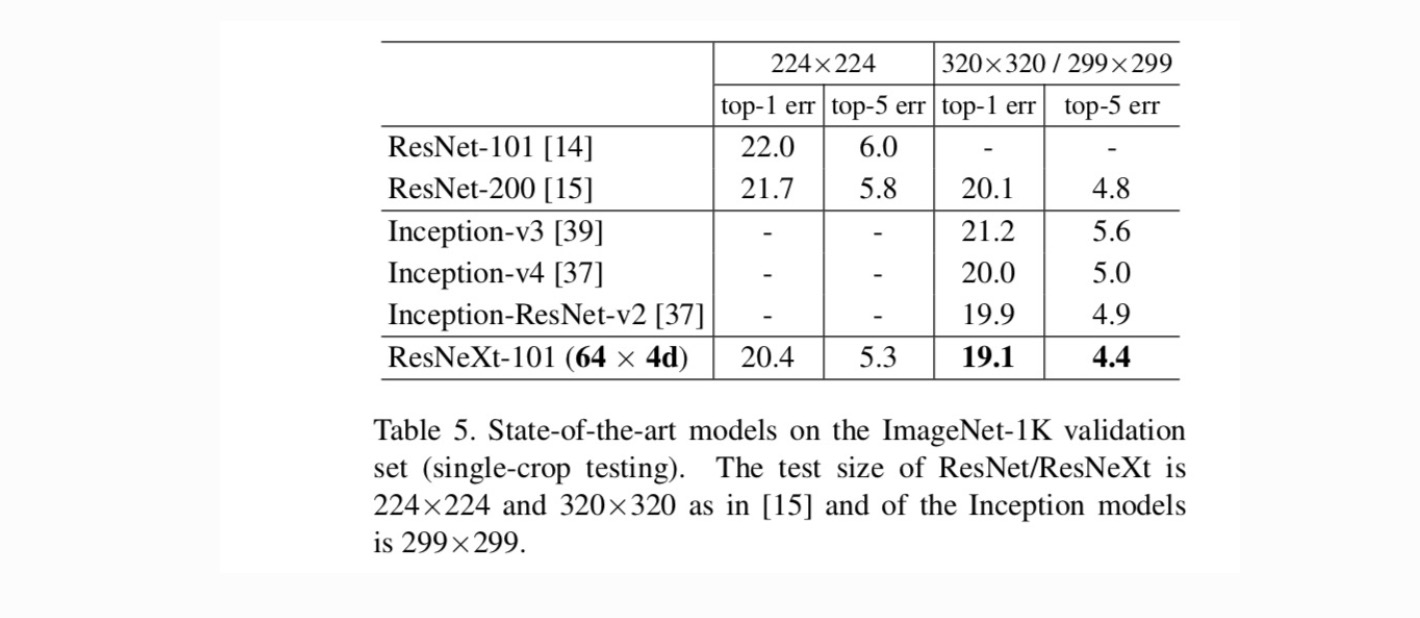
további témák