Posted június 2008.
a földmérés matematikájáról szóló két oszlop közül a második (az első itt található). …
Bill Casselman
University of British Columbia, Vancouver, Kanada
cass at math.ubc.ca
John Eggers
Kaliforniai Egyetem, San Diego jeggers az ucsd-n.edu
 Mail egy barátnak Mail egy barátnak |
 cikk nyomtatása cikk nyomtatása |
a Planiméter egy asztali eszköz a területek mérésére, általában a térképen vagy fényképen lévő szabálytalan régiók területeinek mérésére. Egykor gyakoriak voltak, de mára nagyrészt digitális eszközök váltották fel őket.
az alábbi kép ad némi képet a beállításról. A póluskar szabadon forog az asztalon rögzített pólus körül. A nyomjelző kar a forgócsap körül forog, ahol csatlakozik a sarki karhoz. A nyomjelzővel az óramutató járásával megegyező irányban nyomon követ egy görbét, és ennek során a mérőkerék végiggurul, és a tekercs teljes távolsága felhalmozódik a tárcsán. A tartókerék megakadályozza, hogy a dolog felboruljon. A végén egy számot olvas le a tárcsáról, majd egy tényezővel való szorzás után, csak a Planiméter adott konfigurációjától függően, megkapja a görbe belsejében lévő területet.

a következő ábra jobb képet ad a mechanizmusról.

a kocsit a kerekek, a tárcsa és a forgócsap összeszerelésének nevezzük. A következő képen jobban megnézheti, és láthatja a féreghajtást, amely a tárcsa forgatását okozza, amikor a mérőkerék mozog.

itt van az eredeti Planiméter diagramja, Jakob Amsler cikkéből, amely bevezette:
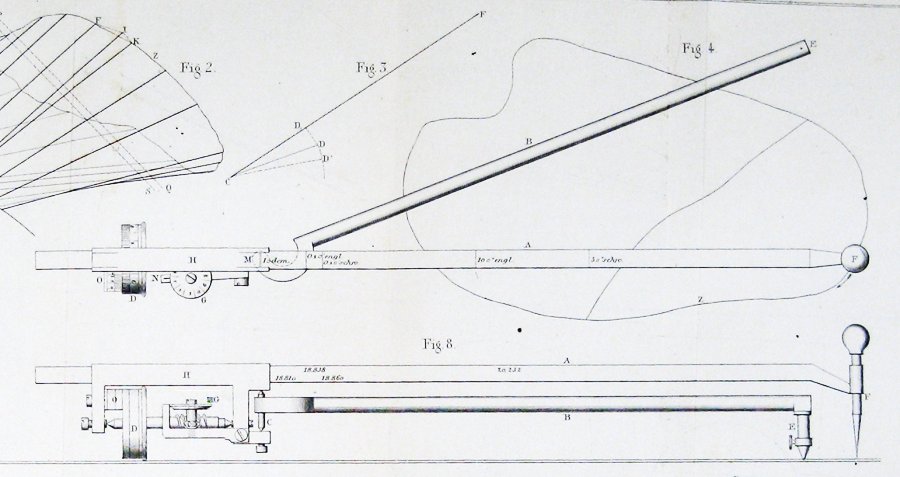
hogyan lehet egy ilyen egyszerű dolog mérni a területeket?
A Planiméter geometriája
a Planiméter óramutató járásával megegyező irányú mozgása ellentétes azzal, amit a matematikusok úgy döntöttek, hogy pozitív forgásnak kell lennie. Ahelyett, hogy megszegnénk ezt az egyezményt, mostantól egy matematikus planiméterével fogunk dolgozni, amelyben az óramutató járásával ellentétes irányban mozog. Mint más matematikusok fantáziái, nincsenek a bolygón!
vannak bizonyos korlátozások a Planiméter elhelyezésére a nyomon követni kívánt görbe tekintetében. A kocsi csúsztatható a nyomjelző kar mentén, de minden esetben a nyomjelző kar l hossza kisebb, mint a póluskar r hossza. Ez azt jelenti, hogy a nyomjelző soha nem juthat el a pólustól r – l távolságra. Másrészt, ha teljesen kinyújtják, a nyomjelző soha nem juthat túl r + l. tehát a nyomon követendő görbének a Gyűrűn belül kell lennie két kör között, az egyik sugarú r – l, a másik r + l.

valójában egy pillanat alatt világossá kell válnia, hogy a karokat soha nem szabad teljesen kinyújtani, ezért a nyomon követendő görbének teljesen a gyűrű belsejében kell lennie. Továbbá, általában a pólus kerül a külső a görbe.

a gyűrű egy adott pontjára a planiméternek pontosan két lehetséges konfigurációja van, amelyek a nyomjelzőt erre a pontra helyezik. Az egyik vagy a másik pont kiválasztása azt jelenti, hogy négyzetgyököt választunk. Ezt nevezzük a Planiméter tájolásának megválasztásának. Pozitív, ha a négyzetgyök pozitív. A tájolás kiválasztása után ugyanaz marad, kivéve, ha a kar teljesen ki van nyújtva. Ez soha nem történhet meg. Mindaddig, amíg a görbe teljes egészében a Gyűrűn belül van, a Planiméter konfigurációi zökkenőmentesen és egyedülállóan változnak a nyomjelző útjával.
a következő dolog az, hogy megértsük néhány dolgot a mérőkerék mozgásáról. Amint az alábbi képen látható, ha a kerék egyenes vonalban halad C távolságban, akkor a kerék egy szögben forog KB = C / R ahol R a sugara.

tehát valóban igaz, hogy a kerék forgása és a nyomjelző kar által megtett távolság valamilyen kapcsolatban áll egymással. De ez a kapcsolat egy kicsit finom. Ha a kar csak egyenesen halad előre egy C távolságot, a kisöpört terület lC lesz, de ha önmagával párhuzamosan eltolódik, akkor a kisöpört terület 0 lesz. Az első esetben a kerék kerületének egy pontja elmozdítja a távolságot C. A második esetben a kerék egyáltalán nem mozog. Ha pedig a kar ferdén fordul, a kerék a kar által lefedett paralelogramma magasságával megegyező távolságot forgat. Minden olyan esetben, amikor a kar önmagával párhuzamosan fordul, a nyomjelző karnak a forgócsap és a nyomjelző közötti része által kisugárzott terület egyenlő lesz lC-vel, ahol C a kerék forgásával mért távolság. Ez az alapvető tény, amely a kar mozgását a mérőkerék mozgásához köti.

ezt pontosan úgy lehet megfogalmazni, hogy függetlenül attól, hogy a kar hogyan mozog, a kerék által mért távolság az út integrálja

ahol a szélesség a kar azon pontja által megtett út, ahol a mérőkerék csatlakozik, n az egységvektor, amely merőleges a karra t az egységvektor, amely a menetirányba mutat (így például, ha a kar önmagával párhuzamosan mozog, n és T pont szorzata 0).
Guldin-tétel
ezután megpróbáljuk a Planiméter viselkedését intuitív módon világossá tenni, de először egy speciális planimétert vizsgálunk, és ebben az esetben egy általánosabb eredményt bizonyítunk. Tegyük fel, hogy veszünk egy l hosszúságú, szabadon mozgó kart, és egy R sugarú mérőkeréket rögzítünk hozzá közvetlenül a közepén.

ezután mozgatjuk a karját a síkon. Ha a mérőkerék a kar mozgása közben a teljes radiánnyi szögben forog, akkor a kerületen lévő pont távolsága C = kb.
Guldin-tétel. Ebben a helyzetben a kar által kiürített teljes terület az lC termék.
a területet itt egy jellel értelmezzük. Ha a kar csak a közepe körül forog, akkor a kar egyik fele előre, a másik hátra megy, a kettő pedig megszűnik.
már láttuk, hogy Guldin állítása érvényes abban az esetben, ha a kar csak fordít. Természetesen ez nem mindig történik meg – a kar foroghat, ahogy mozog,valamint fordít. De láthatjuk, mi történik a söpört terület feldarabolásával az alábbiak szerint:

mivel a mérőkerék a kar közepén van, ahogy a kar forog, az egyik oldalon összenyomja a kis blokkokat, miközben a másik oldalon kitágítja őket. Ezek a hatások pontosan kioltják egymást.
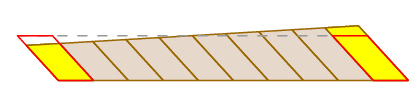
teljesen szigorú bizonyítás adható a változók változásának képletével kettős integrálban, a kerék utazásának kifejezésével pedig útintegrálként.
tegyük fel, hogy a kerék valahol máshol van. Tegyük fel, hogy helyzete c + v, ahol c a kar közepe, v pedig a kar mentén lévő vektor. A v hossza fix marad, mondjuk, hogy a 6. A kerék által követett út c ( t) + v(t). Az útvonal integrál most
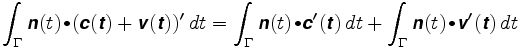
az első integrál az a távolság, amelyet a kerék megtenne, ha a kar közepén lenne. A másodikban a v(t) vektor mindig merőleges n-re, v(t) pedig állandó hosszúságú. A V(t) vektor egy kör sugarú körön mozog, amely egyenlő a kb-val. Ezért az n és v'(t) pont szorzata csak v'(t) aláírt hossza, a második integrál pedig egyenlő a kar teljes forgásának 6-szorosával. Ezért:
ha a kerék a kar középpontjától távol van, akkor a C távolság , amelyet a kerék mér, C0, az a távolság, amelyet akkor mérnének, ha a kerék a középpontban lenne, plusz a kar forgásának teljes dőlésszögének a szorzata.
ennek egy egyszerű esetét azonnal láthatja, ha a karját a középpontja körül forgatja. Ezt Guldin tételével kombinálva azt látjuk, hogy minden esetben:
C = C0 +
kihúzott terület = l C0 = L C – l
a teljes eredmény
Guldin képlete egy aláírt területet ad – ha egy területen visszafelé söpörsz, a kerék hátrafelé megy, és törli a már lefedett területet. Ha ezt arra az esetre alkalmazzuk, amikor a szabad kar pontosan oda tér vissza, ahonnan indult, akkor azt látjuk, hogy az lC egyenlő a kar jobb vége által nyomon követett zárt régió területével, levonva a bal oldali által elsöpört régió területét.
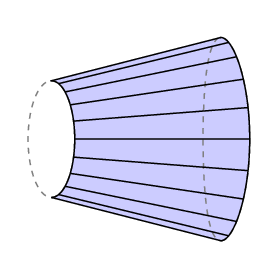
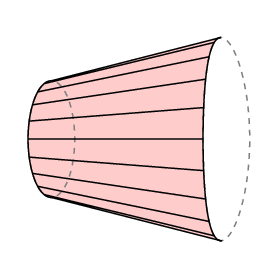

a poláris Planiméter esetében a kar alja az r sugarú kör ívére korlátozódik, középpontja a pólusnál van, ezért l C a terület a nyomkövető lenyomozta. Ezenkívül normális esetben a pólus a mérendő tartományon kívül helyezkedik el, ebben az esetben a kar teljes forgásának 0-nak kell lennie. Tehát ebben az esetben van
terület a régió vezethető = lC
itt az ábra tartalmazza Jakob Amsler, a feltaláló, az ő eredeti papír a műszer feltalálta:
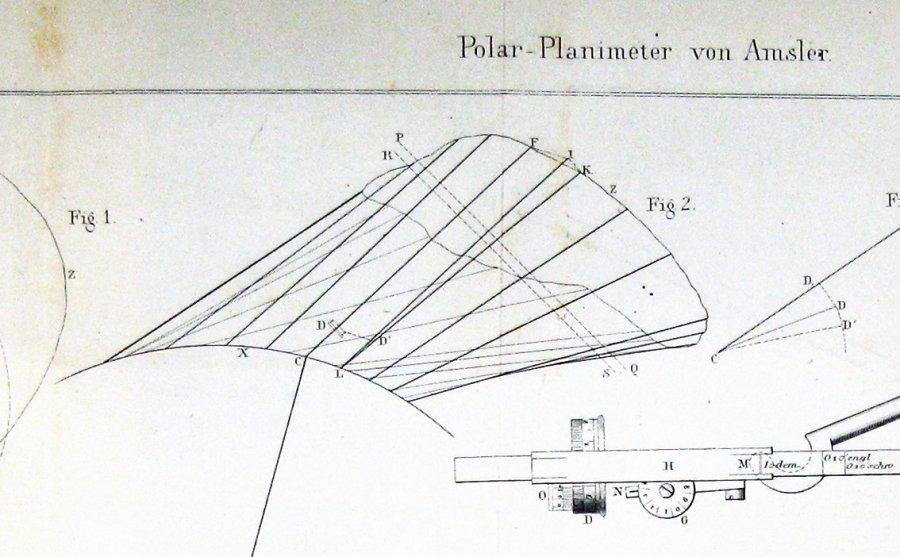
úgy tűnik, elég egyértelmű ebből, hogy Amsler származtatott építése révén valamilyen formában Guldin-tétel.
Planiméterek és Green tétele
mint már említettük, Miután kiválasztottuk a Planiméter tájolását, a Planiméter konfigurációja a nyomjelző helyzetének folyamatos függvénye. Tegyük fel, hogy a pozitív orientációt választjuk. Ezután a gyűrű minden pontjához rögzíthetünk egy n egységvektort, amely az óramutató járásával ellentétes irányba mutat, merőleges a nyomjelző karra a nyomjelzőnél.
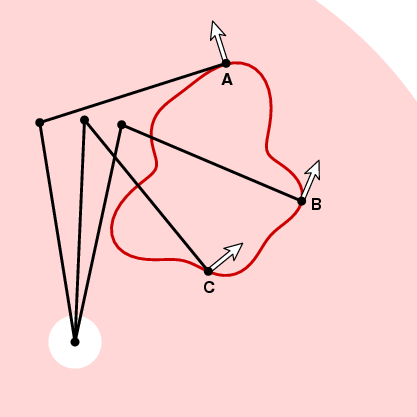
az, hogy a mérőkerék hogyan reagál a görbe mentén történő mozgásra a következő pillanatban, attól függ, hogy ez a vektor milyen szöget zár be a görbe egység érintő vektorával. A fenti képen A mérőkerék nem fog mozogni, mert a görbe mentén a mozgás párhuzamos a nyomjelző karral. B-nél, ha a nyomjelző kis távolságot mozog ds, így lesz a mérőkerék is. És C-nél a mérőkerék bizonyos távolságot mozog 0 és ds között. Pontosabban tegyük fel, hogy t az egység érintő vektor a görbe egy pontján. Ha a nyomjelző DS távolságot mozog a görbe mentén, akkor a mérőkerék d DS távolságot fog mozgatni, ahol d = n . t, az egységvektorok pont szorzata t és n. más szóval, ha a görbe körül mozogunk, akkor a mérőkerék teljes távolsága megegyezik n integráljával . t DS (Dot termék), vagy

de mivel a gyűrű minden pontja megfelel a Planiméter egyedi pozitív konfigurációjának, hozzárendelhetünk egy vektort n a gyűrű minden belső pontjához, ezért meghatároz egy vektormezőt. A görbe a belső határa, és az egyik feltételezésünk szerint ez teljes egészében abban a régióban található, ahol n definiálva van. Green tétele azt mondja nekünk, hogy ennek a régiónak a határa körüli útintegrál egyenlő egy bizonyos integrállal is a felett!): Ezért
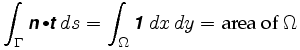
pontosabban, Green tétele azt mondja nekünk, hogy
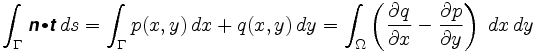
ahol n = az érintett vektormező. A kettős integrál integrandusát a vektor mező görbületének nevezzük.
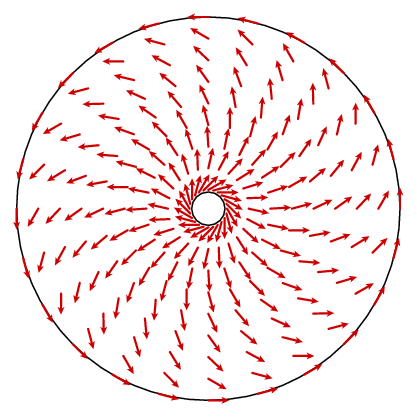
úgy tűnik, hogy ez nem vezet túl messzire. Mi kellene történnie, hogy a curl egy állandó 1. Elvileg találhatnánk egy képletet az n vektormezőre, és kiszámolhatnánk annak görbületét, de ez nem túl felvilágosító. Egy másik tényt azonban kihasználhatunk. A vektormező körkörös szimmetriával rendelkezik, ami azt jelenti, hogy azt az határozza meg, hogy mi van egy sugáron. A koszinusz törvény egyszerű képletet ad a kerületi komponensre.
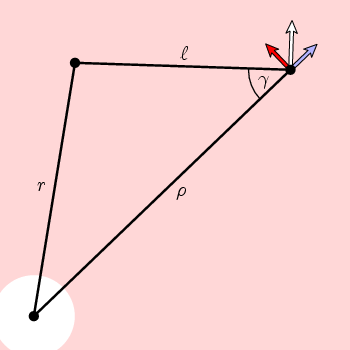
az ábrán látható egyszerű geometriából következik, hogy az n kerületi komponense
f ( ~ ) = cos ( ~ ) = (~2 + l 2 – r 2)/(2 ~ l)
Green tételének valódi pontja az, hogy annak igazolásához, hogy az integrandus 1, elegendő annak ellenőrzése, hogy a megfelelő kis utak körüli integrál útvonala ugyanaz, mint a terület. Ehhez úgy választjuk meg régiónkat, mint itt: 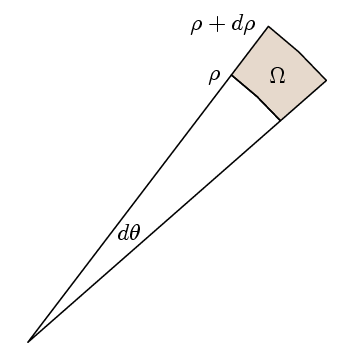
Akkor l-szor az út integral
l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ
vagy
(θ/2) ( (ρ + dp) 2 – ρ 2)
egyéb típusú planiméterek
Guldin tétele azt jelenti, hogy a mérőkerék mozgása megmondja a nyomjelző által nyomon követett területet, amikor a kar egy mérőkerékkel nyomon követi a görbét, de az egyik vége egydimenziós görbére korlátozódik. Ez történik például a gördülő síkmérővel, amelyben a forgócsapot egyenes vonalra korlátozzák azáltal, hogy gördülő hengeren vannak.

további információkért
-
 még mindig gyárt és értékesít planimétereket.
még mindig gyárt és értékesít planimétereket. - differenciál-és integrálszámítás Volume II, R. Courant, Blackie& Son, 1936. A Guldin-képletről szóló szakasz (294-298.o.) magyarázatot ad a Planiméter működésére.
- Amsler eredeti cikke, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Ez hiányzik a diagramok, de itt vannak:
- Amsler első diagramja
- Amsler második diagramja
köszönet Donna Sammisnek a Stony Brook egyetemi könyvtárból a cikk megtalálásáért és férjének, Robertnek, hogy fényképeket szolgáltatott az ábrákról.
az Amsler által alapított vállalat már a 20. században gyártott hangszereket. Ez a fénykép a logót mutatja a Planiméter áramszedős változatán:

- “a Planiméterekről,” EngineerSupply. A cég videót is közzétett a YouTube-on.
Bill Casselman
University of British Columbia, Vancouver, Kanada
cass at math.ubc.ca
John Eggers
Kaliforniai Egyetem, San Diego ucsd.edu
azok, akik hozzáférhetnek a JSTOR-hoz, megtalálhatják a fent említett papírokat. Azok számára, akik hozzáférnek, az American Mathematical Society MathSciNet lehet használni, hogy további bibliográfiai információk és vélemények néhány ilyen anyagok. A fenti elemek egy része elérhető az ACM portálon keresztül , amely bibliográfiai szolgáltatásokat is nyújt.