A Sobel operátor varázsa

Julius Drost képe az Unsplash-en

végül, abban a pillanatban, amire mindannyian vártatok, a következő a felügyelet nélküli Bayes-I következtetési sorozat: (nem annyira) mély merülésünk a Sobel Operátorba.

egy igazán varázslatos élérzékelő algoritmus, amely lehetővé teszi az alacsony szintű funkciók kibontását és a dimenzió csökkentését, lényegében csökkentve a kép zaját. Különösen hasznos volt az arcfelismerő alkalmazásokban.

Irwin Sobel és Gary Feldman (Stanford Artificial Intelligence Laboratory) 1968-as szerelmi gyermeke, ez az algoritmus inspirálta számos modern éldetektálási technikát. Két ellentétes mag vagy maszk konvolválásával egy adott kép fölé (pl. lásd alább-balra) (mindegyik képes vízszintes vagy függőleges élek észlelésére), létrehozhatunk egy kevésbé zajos, kisimított ábrázolást (lásd alább-jobbra).

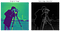
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel értékek (általában fénysűrűség) az egyes pixelek (a horgony pixel) és a környező pixelek közötti különbség megkülönböztetésével (lényegében egy kép deriváltjának közelítésével).

Ez az eredeti kép simítását eredményezi, és alacsonyabb dimenziós kimenetet eredményez, ahol az alacsony szintű geometriai jellemzők tisztábban láthatók. Ezek a kimenetek ezután felhasználhatók bonyolultabb osztályozási algoritmusok bemeneteként, vagy példaként a felügyelet nélküli valószínűségi fürtözéshez Kullback-Leibler divergencia (KLD) (amint az az LBP legutóbbi blogomban látható).

Az alacsonyabb dimenziós kimenet generálásához meg kell vennünk a kép deriváltját. Először kiszámítjuk a származékot mind az x, mind az y irányban. Két 3×3-as magot hozunk létre (lásd mátrixok), nullákkal a megfelelő tengely közepe mentén, kettővel a középső négyzetekben, merőlegesen a középső nullára, egyesekkel az egyes sarkokban. A nem nulla értékek mindegyikének pozitívnak kell lennie a nullák tetején/jobb oldalán (tengelytől függően), negatívnak pedig a megfelelő oldalon. Ezeket a kerneleket Gx-nek és Gy-nek nevezik.

ezek a következő formátumban jelennek meg:

ezek a kernelek ezután a kép fölé kerülnek, minden kernel központi pixelét a kép minden pixelére helyezve. Mátrixszorzással számítjuk ki egy új megfelelő pixel intenzitási értékét a kimeneti képen, minden kernelhez. Ezért két kimeneti képet kapunk (mindegyik derékszögű irányhoz egyet).

a cél az, hogy megtaláljuk a különbséget/változást a képen látható pixel és a gradiens mátrix (kernel) összes pixelje között (Gx és Gy). Matematikailag ez kifejezhető.

Mellékjegyzet:

technikailag nem konvolving semmit. Bár az AI és a gépi tanulás körében a ‘konvolúciókra’ szeretünk hivatkozni, a konvolúció magában foglalná az eredeti kép megfordítását. Matematikailag, amikor konvolúciókra utalunk, valójában kiszámítjuk a bemenet minden 3×3 területe és az egyes pixelek maszkja közötti keresztkorrelációt. A kimeneti kép a maszk és a bemenet közötti teljes kovariancia. Így érzékelik az éleket.

vissza a Sobel magyarázathoz…

a maszk és a bemenet 3×3 szakasza közötti mátrixszorzáshoz kiszámított értékeket összegezzük, hogy a kimeneti kép pixelének végső értékét kapjuk. Ez egy új képet hoz létre, amely információkat tartalmaz az eredeti képen lévő függőleges és vízszintes élek jelenlétéről. Ez az eredeti kép geometriai ábrázolása. Továbbá, mivel ez az operátor garantáltan ugyanazt a kimenetet állítja elő minden alkalommal, ez a technika lehetővé teszi a képszegmentálási feladatok stabil élérzékelését.

ezekből a kimenetekből kiszámolhatjuk mind a gradiens nagyságát, mind a gradiens irányát (az arctangent operátor segítségével) bármely adott pixelnél (x,y):

ezzel megállapíthatjuk, hogy azok a pixelek, amelyek nagy nagyságrendűek, nagyobb valószínűséggel lesznek a kép élei, míg az irány tájékoztat minket az él tájolásáról (bár az irány nem szükséges a kimenetünk előállításához).

egyszerű megvalósítás:

itt van egy egyszerű végrehajtása a Sobel operátor python (a NumPy), hogy kapsz egy érzést a folyamat (az összes bimbózó kódolók odakinn).

Ez a megvalósítás a Wikipedia pszeudokód példájának python változata, amelynek célja, hogy megmutassa, hogyan lehet végrehajtani ezt az algoritmust, miközben bemutatja a folyamat különböző lépéseit is.

miért érdekel minket?

bár az operátor által előállított gradiens közelítés viszonylag durva, rendkívül számítási szempontból hatékony módszert kínál a képek éleinek, sarkainak és egyéb geometriai jellemzőinek kiszámítására. Viszont, ez előkészítette az utat számos dimenzió csökkentése és a funkció kitermelése technikák, mint például a helyi bináris minták (lásd a másik blog további részleteket ezt a technikát).

a kizárólag geometriai jellemzőkre támaszkodva fennáll annak a veszélye, hogy adataink kódolása során fontos információkat veszítünk el, azonban a kompromisszum az, ami lehetővé teszi az adatok gyors előfeldolgozását és a gyors képzést. Ezért ez a technika különösen hasznos olyan esetekben, amikor a textúra és a geometriai jellemzők rendkívül fontosnak tekinthetők a bemenet meghatározásakor. Ez az oka annak, hogy az arcfelismerés viszonylag nagy pontossággal elvégezhető a Sobel operátor segítségével. Ez a technika azonban nem biztos, hogy a legjobb választás, ha olyan bemeneteket próbál osztályozni vagy csoportosítani, amelyek a színt használják fő megkülönböztető tényezőként.

Ez a módszer még mindig rendkívül hatékony a geometriai jellemzők alacsony dimenziós ábrázolásához és kiváló kiindulópont a dimenzió és a zaj csökkentéséhez, mielőtt más osztályozókat használna, vagy a bayesi következtetési módszertanokban való felhasználásra.