Bevezetés a mozgás becsléséhez optikai áramlással

ebben a bemutatóban az optikai áramlás alapjaiba merülünk, megnézzük néhány alkalmazását és megvalósítjuk két fő változatát (ritka és sűrű). Röviden megvitatjuk a legújabb megközelítéseket is, amelyek mély tanulást és ígéretes jövőbeli irányokat használnak.

a számítógépes látás kutatásának legújabb áttörései lehetővé tették a gépek számára, hogy érzékeljék a környező világot olyan technikákkal, mint az objektumdetektálás egy bizonyos osztályba tartozó objektumok példányainak kimutatására, valamint a szemantikai szegmentálás a pixel-osztályozáshoz.

a valós idejű videobemenet feldolgozásához azonban ezeknek a technikáknak a legtöbb megvalósítása csak az azonos kereten belüli objektumok kapcsolatait kezeli \((x, y)\) figyelmen kívül hagyva az időinformációkat \((t)\). Más szavakkal, az egyes képkockákat egymástól függetlenül újraértékelik, mintha teljesen független képek lennének, minden egyes futtatáshoz. Mi van azonban, ha szükségünk van az egymást követő keretek közötti kapcsolatokra, például nyomon akarjuk követni a járművek mozgását a keretek között, hogy megbecsüljük az aktuális sebességet és megjósoljuk a helyzetét a következő keretben?

vagy, alternatívaként, mi van, ha információra van szükségünk az egymást követő keretek közötti emberi pózkapcsolatokról, hogy felismerjük az emberi tevékenységeket, például az íjászatot, a baseballt és a kosárlabdát?

ebben az oktatóanyagban megtanuljuk, mi az optikai áramlás, hogyan valósítsuk meg két fő változatát (ritka és sűrű), és átfogó képet kapunk a legújabb megközelítésekről, amelyek mély tanulást és ígéretes jövőbeli irányokat tartalmaznak.

mi az optikai áramlás?
végrehajtási ritka optikai Flow
végrehajtási sűrű optikai Flow
mély tanulás és azon túl

mi az optikai flow?

kezdjük az optikai áramlás magas szintű megértésével. Az optikai áramlás az objektumok egymást követő képkockák közötti mozgása, amelyet az objektum és a kamera közötti relatív mozgás okoz. Az optikai áramlás problémája a következőképpen fejezhető ki:

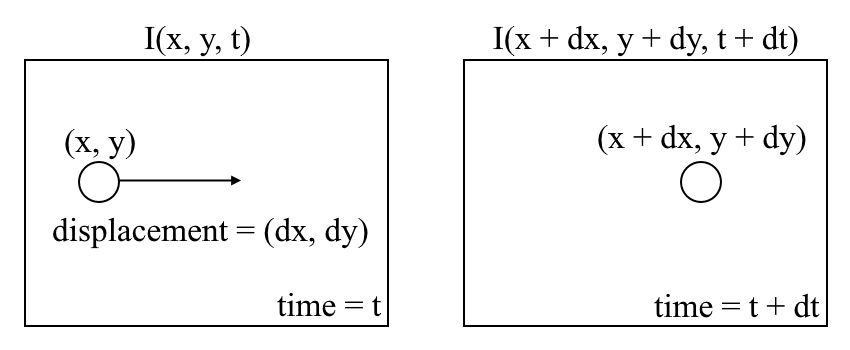
ahol az egymást követő keretek között kifejezhetjük a kép intenzitását \((i)\) a tér függvényében \((x, y)\) és az idő \((T)\). Más szóval, ha az első képet \ (I (x, y, t)\) és a képpontjait \((dx, dy)\) idő alatt mozgatjuk, akkor megkapjuk az új képet \(I(x + dx, y + dy, t + dt)\).

először azt feltételezzük, hogy egy objektum pixelintenzitása állandó az egymást követő keretek között.

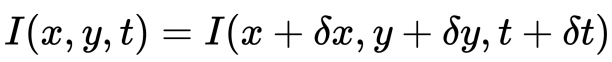
másodszor, vesszük az RHS Taylor sorozat közelítését, és eltávolítjuk a közös kifejezéseket.

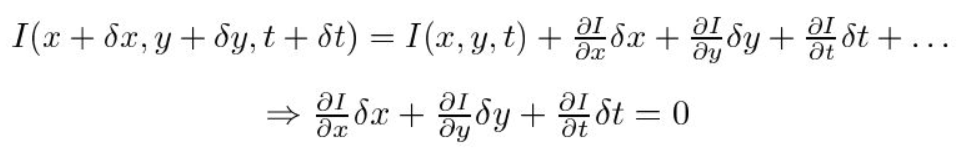
harmadszor, osztjuk \(dt\) levezetni az optikai áramlási egyenlet:

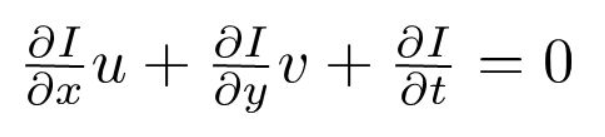
ahol \(u = dx/dt\) és \(v = dy/dt\).

\(dI/dx, dI/dy\) és \(dI/dt\) a képgradiensek a vízszintes tengely, a függőleges tengely és az idő mentén. Ezért az optikai áramlás problémájával zárulunk, Vagyis megoldjuk \(u (dx/dt)\) és \(v (dy/dt)\) a mozgás időbeli meghatározására. Észrevehetjük, hogy nem tudjuk közvetlenül megoldani a \(u\) és \(v\) optikai áramlási egyenletét, mivel csak egy egyenlet van két ismeretlen változóra. Néhány módszert, például a Lucas-Kanade módszert fogunk végrehajtani a probléma megoldására.

ritka vs sűrű optikai áramlás

a ritka optikai áramlás néhány “érdekes tulajdonság” (mondjuk néhány képpont, amely egy objektum széleit vagy sarkait ábrázolja) áramlási vektorát adja a kereten belül, miközben sűrű optikai áramlás, amely a teljes keret (minden pixel) áramlási vektorait adja – pixelenként legfeljebb egy áramlási vektor. Ahogy sejtette volna, a sűrű optikai áramlás nagyobb pontossággal rendelkezik, mivel lassú/számítási szempontból drága.

ritka optikai áramlás végrehajtása

ritka optikai áramlás a pixelek ritka funkciókészletét választja ki (például érdekes funkciók, például élek és sarkok) a sebességvektorok (mozgás) nyomon követéséhez. A kibontott funkciókat az optikai áramlás funkció keretről keretre továbbítja annak biztosítása érdekében, hogy ugyanazokat a pontokat kövessék. A ritka optikai áramlásnak számos megvalósítása létezik, beleértve a Lucas–Kanade módszert, a Horn–Schunck módszert, a Buxton–Buxton módszert és így tovább. A Lucas-Kanade módszert az OpenCV-vel, a számítógépes látás algoritmusok nyílt forráskódú könyvtárával fogjuk használni a megvalósításhoz.

A környezet beállítása

Ha még nincs telepítve az OpenCV, nyissa meg a terminált és futtassa:

pip install opencv-python

most klónozza a bemutató adattárat a futással:

git clone https://github.com/chuanenlin/optical-flow.git

következő, nyissa meg a sparse-starter.py a szövegszerkesztővel. Az összes kódot ebben a Python fájlban fogjuk írni.

az OpenCV beállítása videó olvasására és paraméterek beállítása

Shi-Tomasi Corner Detector – a követendő pixelek kiválasztása

a ritka optikai áramlás megvalósításához csak egy funkciókészlet pixeleinek mozgását követjük nyomon. A képek jellemzői olyan érdekes pontok, amelyek gazdag képtartalmi információkat tartalmaznak. Ilyen jellemzők lehetnek például a kép olyan pontjai, amelyek változatlanok a fordítás, a méretarány, az elforgatás és az intenzitásváltozások, például a sarkok szempontjából.

A Shi-Tomasi Sarokdetektor nagyon hasonlít a népszerű Harris Sarokdetektorhoz, amely a következő három eljárással valósítható meg:

1. határozza meg az ablakokat (kis képfoltok) nagy színátmenetekkel (a képintenzitás variációi), ha \(x\) és \(y\) irányba fordítják.
2. minden ablakhoz számítson ki egy \(R\) pontszámot.
3. A \(R\) értékétől függően minden ablak sík, él vagy sarok kategóriába kerül.

Ha többet szeretne tudni a Harris Corner detektor lépésről lépésre történő matematikai magyarázatáról, nyugodtan nézze át ezeket a diákat.

Shi és Tomasi később egy kicsi, de hatékony módosítást végeztek a Harris Corner detektoron a papírjukban.

a módosítás arra az egyenletre vonatkozik, amelyben a \(R\) pontszámot kiszámítják. A Harris Corner detektorban a pontozási funkciót a:

$$
\begin{array}{c}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\newline \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\end{array}
$$

ehelyett shi-Tomasi a pontozási függvényt javasolta:

$$
R=\min \left(\lambda_{1}, \lambda_{2}\right)
$$

ami alapvetően azt jelenti, hogy ha \(r\) nagyobb, mint egy küszöb, akkor saroknak minősül. A következőkben Harris (balra) és Shi-Tomasi (jobbra) pontozási függvényeit hasonlítjuk össze a \(61-2\) térben.

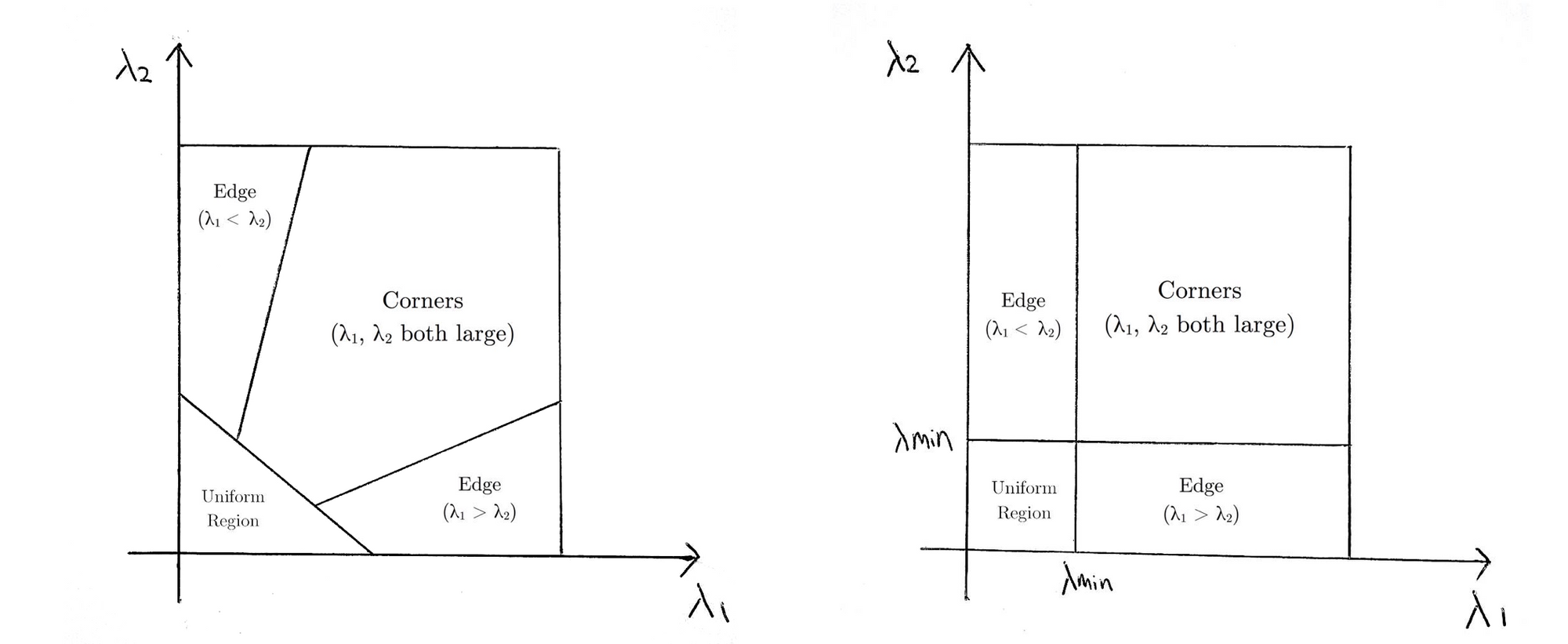
A Shi-Tomasi esetében csak akkor minősül saroknak az ablak, ha a \(61\) és \2\) egy minimális küszöbérték felett van.

az OpenCV shi-Tomasi implementációjának dokumentációja a goodFeaturesToTrack() segítségével itt található.

meghatározott objektumok követése

lehetnek olyan esetek, amikor csak egy adott érdekes objektumot (mondjuk egy bizonyos személy nyomon követését) vagy egy objektumkategóriát szeretne követni (mint például a forgalomban lévő összes 2 wheeler-jármű). A prev változó megváltoztatásával könnyen módosíthatja a kódot a kívánt objektum(ok) pixeleinek nyomon követéséhez.

ezzel a módszerrel kombinálhatja az Objektumérzékelést is, hogy csak a pixelek áramlását becsülje meg az észlelt határoló mezőkön belül. Így nyomon követheti a videó egy adott típusának/kategóriájának összes objektumát.

Lucas-Kanade: ritka optikai áramlás

Lucas és Kanade hatékony technikát javasolt az érdekes funkciók mozgásának becslésére, összehasonlítva két egymást követő képkockát a tanulmányukban egy iteratív Képregisztrációs technikával a sztereó látás alkalmazásával. A Lucas-Kanade módszer a következő feltételezések szerint működik:

1. két egymást követő képkockát egy kis időnövelés választ el egymástól (\(dt\)) úgy, hogy az objektumok ne mozduljanak el jelentősen (más szóval, a módszer a legjobban lassan mozgó tárgyakkal működik).
2. a keret egy “természetes” jelenetet ábrázol, texturált tárgyakkal, amelyek szürke árnyalatokat mutatnak, amelyek simán változnak.

először is, ezen feltételezések alapján egy kis 3×3-as ablakot (szomszédságot) vehetünk a Shi-Tomasi által észlelt jellemzők körül, és feltételezhetjük, hogy mind a kilenc pontnak ugyanaz a mozgása van.

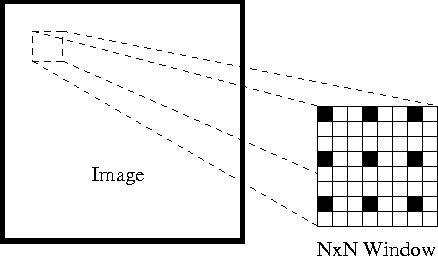
Ez lehet ábrázolni, mint

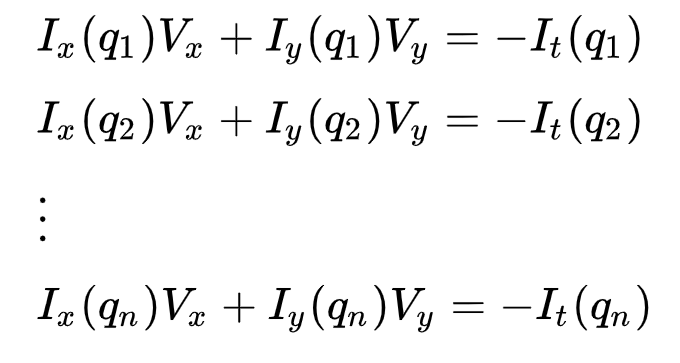
ahol \(q_1, q_2,…, q_n\) az ablakon belüli pixeleket jelöli (pl. \(N\) = 9 egy 3×3-as ablak esetében) és \(i_x(q_i)\), \(i_y(q_i)\), és \(i_t(q_i)\) a kép \(I\) részleges deriváltjait jelöli a \(X, Y) pozícióhoz képest\ ((X, Y)\) és az idő\ (t\), a pixel\ (q_i\) az aktuális időben.

Ez csak az optikai áramlási egyenlet (amelyet korábban leírtunk) az egyes n pixelekre.

az egyenletek halmaza a következő mátrixformában ábrázolható, ahol \(Av = b\):

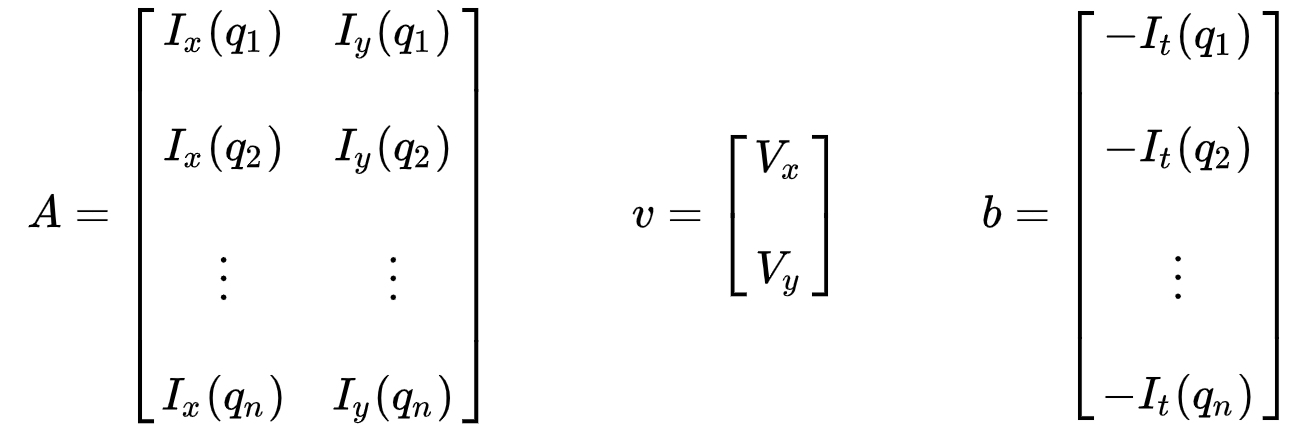
vegye figyelembe, hogy korábban (lásd: “mi az optikai áramlás?”szakasz), szembesültünk azzal a kérdéssel, hogy két ismeretlen változót kell megoldanunk egy egyenlettel. Most két ismeretlenre (\(V_x\) és \(V_y\)) kell megoldanunk kilenc egyenletet, ami túl van meghatározva.

másodszor, hogy foglalkozzon a túl meghatározott kérdés, alkalmazzuk legkisebb négyzetek illeszkedő, így a következő két egyenlet-két ismeretlen probléma:

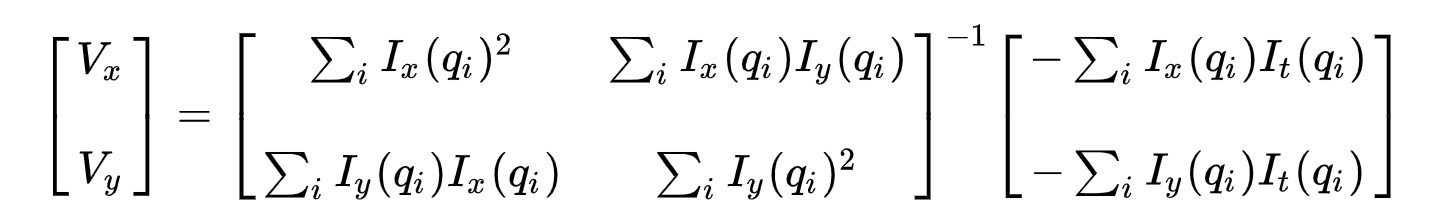
ahol \(VX = u = DX/DT\) a \(X\) időbeli mozgását, \(vy = v = dy/DT\) pedig y időbeli mozgását jelöli. A két változó megoldása befejezi az optikai áramlási problémát.

dióhéjban azonosítunk néhány érdekes funkciót ezen pontok optikai áramlási vektorainak nyomon követésére és iteratív kiszámítására. A Lucas-Kanade módszer elfogadása azonban csak kis mozgásokra működik (kezdeti feltételezésünk szerint), és nagy mozgás esetén kudarcot vall. Ezért a Lucas-Kanade módszer OpenCV megvalósítása piramisokat alkalmaz.

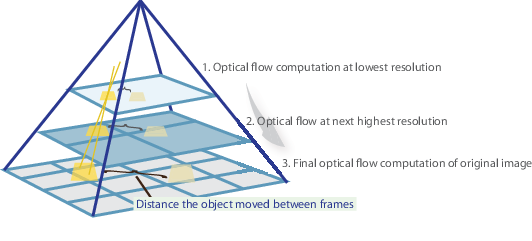
magas szintű nézetben a kis mozgásokat elhanyagoljuk, amikor felmegyünk a piramisba, a nagy mozgásokat pedig kis mozgásokra redukáljuk-kiszámítjuk az optikai áramlást a skálával együtt. Az OpenCV megvalósításának átfogó matematikai magyarázata megtalálható Bouguet jegyzeteiben, valamint a Lucas-Kanade módszer OpenCV általi megvalósításának dokumentációja a calcOpticalFlowPyrLK() segítségével itt található.

vizualizálás

és ennyi! Nyissa meg a terminált, és futtassa a

python sparse-starter.py

a ritka optikai áramlás implementációjának teszteléséhez. ha elmulasztott egy kódot, a teljes kód a következő helyen található: sparse-solution.py.

sűrű optikai áramlás megvalósítása

korábban kiszámítottuk az optikai áramlást egy ritka pixelkészlethez. Sűrű optikai áramlás megpróbálja kiszámítani az optikai áramlási vektort minden képponthoz. Bár az ilyen számítás lassabb lehet, pontosabb eredményt és sűrűbb eredményt ad olyan alkalmazásokhoz, mint például a mozgás és a videó szegmentálás tanulási struktúrája. A sűrű optikai áramlásnak különféle megvalósításai vannak. A Farneback módszert fogjuk használni, az egyik legnépszerűbb megvalósítás, az OpenCV használatával, a számítógépes látás algoritmusok nyílt forráskódú könyvtára, a megvalósításhoz.

A környezet beállítása

Ha még nem tette meg, kövesse a ritka optikai áramlás végrehajtásának 1.lépését a környezet beállításához.

következő, nyitott dense-starter.py a szövegszerkesztővel. Az összes kódot ebben a Python fájlban fogjuk írni.

az OpenCV beállítása videó olvasására

Farneback optikai áramlás

Gunnar Farneback hatékony technikát javasolt az érdekes tulajdonságok mozgásának becslésére két egymást követő képkocka összehasonlításával a polinom Táguláson alapuló két képkockás Mozgásbecslésben.

először is, a módszer közelíti a képkeretek ablakait (lásd Lucas Kanade szakasz ritka optikai áramlás megvalósítás további részletekért) kvadratikus polinomok révén polinom expanziós transzformáció. Másodszor, megfigyelve, hogy a polinom hogyan alakul át fordítás (mozgás) alatt, meghatározunk egy módszert az elmozdulási mezők becslésére a polinom tágulási együtthatóiból. Finomítások sorozata után kiszámítják a sűrű optikai áramlást. Farneback papír meglehetősen tömör és egyszerű követni, ezért nagyon ajánlom megy át a papírt, ha azt szeretné, hogy jobban megértsék a matematikai levezetés.

az OpenCV megvalósításához kiszámítja az optikai áramlás nagyságát és irányát az áramlási Vektorok 2 csatornás tömbjéből \((dx/dt, dy/dt)\), az optikai áramlás problémája. Ezután megjeleníti az áramlás szögét (irányát) színárnyalattal, az áramlás távolságát (nagyságát) pedig a HSV színábrázolás értékével. Az optimális láthatóság érdekében a HSV erőssége mindig legfeljebb 255-re van állítva. Az OpenCV Farneback metódus implementációjának dokumentációja a calcOpticalFlowFarneback() segítségével itt található.

vizualizálás

és ennyi! Nyissa meg a terminált és futtassa

python dense-starter.py

a sűrű optikai áramlás implementációjának teszteléséhez. ha elmulasztott egy kódot, a teljes kód a következő helyen található: dense-solution.py.

optikai áramlás mély tanulással

míg az optikai áramlás problémája történelmileg optimalizálási probléma volt, a mély tanulás alkalmazásával kapcsolatos legújabb megközelítések lenyűgöző eredményeket mutattak. Általában az ilyen megközelítések két videokeretet vesznek fel bemenetként az optikai áramlás (színkódolt kép) kimenetéhez, amely a következőképpen fejezhető ki:

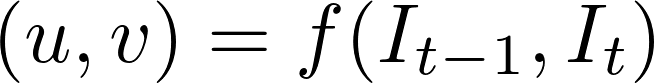
ahol \(u\) az \(x\) irányú mozgás, \(v\) az \(y\) irányú mozgás, és \(f\) egy neurális hálózat, amely két egymást követő képkockát vesz fel \(i_{t-1}\) (frame at time = \(t-1)\) és \(i_t\) (frame at time = \(t)\) mint bemenet.

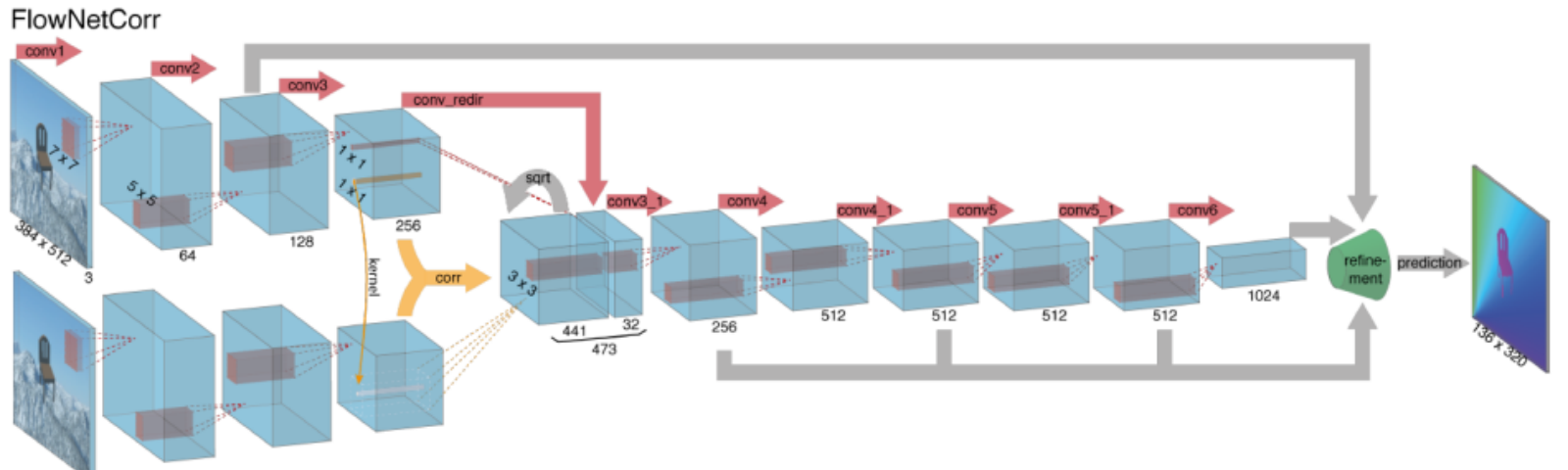
Az optikai áramlás mély neurális hálózatokkal történő kiszámításához nagy mennyiségű képzési adat szükséges, amelyet különösen nehéz megszerezni. Ennek oka az, hogy a videofelvételek optikai áramláshoz történő címkézéséhez pontosan meg kell határozni a kép minden egyes pontjának pontos mozgását az alpixel pontosságig. A címkézési képzési adatok kérdésének kezelése érdekében a kutatók számítógépes grafikát használtak a hatalmas reális világok szimulálására. Mivel a világokat utasítások generálják, a kép minden egyes pontjának mozgása egy videó sorozatban ismert. Néhány példa erre az MPI-Sintel, egy nyílt forráskódú CGI film optikai áramlás címkézés különféle szekvenciákhoz renderelve, valamint repülő székek, sok, véletlenszerű háttérrel repülő szék adatkészlete, optikai áramlás címkézéssel is.

Az optikai áramlási problémák megoldása a mély tanulással jelenleg rendkívül aktuális téma, a FlowNet, a SPyNet, a PWC-Net stb.

optikai áramlás alkalmazás: szemantikai szegmentálás

az optikai áramlási mező hatalmas információbánya a megfigyelt jelenet számára. Ahogy az optikai áramlás pontos meghatározásának technikái javulnak, érdekes látni az optikai áramlás alkalmazását számos más alapvető számítógépes látásfeladattal való találkozáskor. Például a szemantikai szegmentálás feladata egy kép felosztása egyedi objektumosztályoknak megfelelő régiók sorozatára, mégis az azonos textúrájú, szorosan elhelyezett objektumok gyakran nehézek az egykockás szegmentálási technikáknál. Ha azonban az objektumokat külön helyezik el, akkor az objektumok különálló mozgása nagyon hasznos lehet, ha a sűrű optikai áramlási mező folytonossága megfelel az objektumok közötti határoknak.

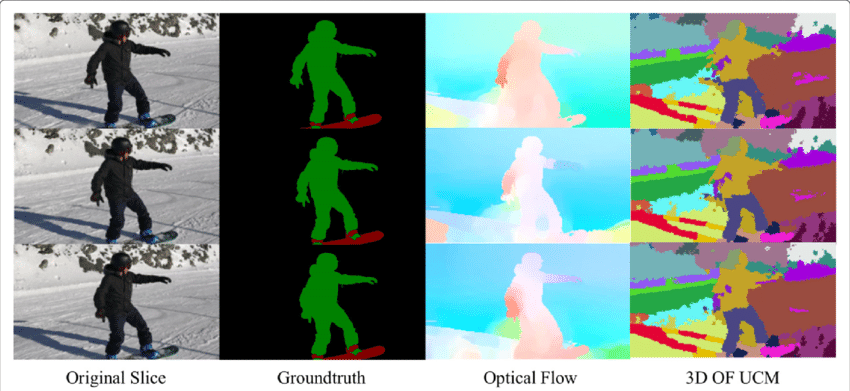
Optical Flow application: Object Detection & Tracking

Az optikai áramlás másik ígéretes alkalmazása lehet az objektumérzékelés és-követés, vagy magas szintű formában, valós idejű járműkövető és forgalomelemző rendszerek kiépítése felé. Mivel a ritka optikai áramlás az érdekes pontok nyomon követését használja, az ilyen valós idejű rendszereket funkcióalapú optikai áramlási technikákkal lehet végrehajtani akár helyhez kötött kamerából, akár járművekhez csatlakoztatott kamerákból.

következtetés

alapvetően az optikai áramlási Vektorok számtalan magasabb szintű feladat bemeneteként működnek, amelyek a videó szekvenciák jelenet megértését igénylik, miközben ezek a feladatok még összetettebb rendszerek építőkövei lehetnek, mint például az arckifejezés elemzése, az autonóm jármű navigáció és még sok más. Az optikai áramlás még felfedezésre váró új alkalmazásait csak a tervezők találékonysága korlátozza.

lusta kódolni, nem akar költeni GPU-kra? Irány a Nanonets és épít számítógépes látás modellek ingyen!