Felügyelet nélküli Feature Learning and Deep Learning Tutorial

Bevezetés

a főkomponens-elemzés (PCA) egy dimenziócsökkentő algoritmus, amely jelentősen felgyorsíthatja a felügyelet nélküli feature learning algoritmust. Ennél is fontosabb, hogy a PCA megértése lehetővé teszi számunkra, hogy később megvalósítsuk a fehérítést, ami sok algoritmus fontos előfeldolgozási lépése.

tegyük fel, hogy az algoritmust képekre képzi. Ezután a bemenet kissé redundáns lesz, mert a kép szomszédos képpontjainak értékei erősen korrelálnak. Konkrétan tegyük fel, hogy 16×16 szürkeárnyalatos képfoltokon edzünk. Ezután a \ textstyle x \ in \ Re^{256} 256 dimenziós vektor, amelynek egy jellemzője a \ textstyle x_j, amely megfelel az egyes pixelek intenzitásának. A szomszédos pixelek közötti korreláció miatt a PCA lehetővé teszi számunkra, hogy a bemenetet sokkal alacsonyabb dimenzióval közelítsük meg, miközben nagyon kevés hibát okozunk.

példa és matematikai háttér

futó példánkhoz egy \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} adatkészletet fogunk használni \textstyle n=2 dimenziós bemenettel, így a \textstyle x^{(i)} \in \Re^2. Tegyük fel, hogy az adatokat 2 dimenzióról 1-re akarjuk csökkenteni. (A gyakorlatban érdemes lehet az adatokat 256-ról 50 dimenzióra csökkenteni; de az alacsonyabb dimenziós adatok használata példánkban lehetővé teszi az algoritmusok jobb megjelenítését.) Itt van az adatkészletünk:

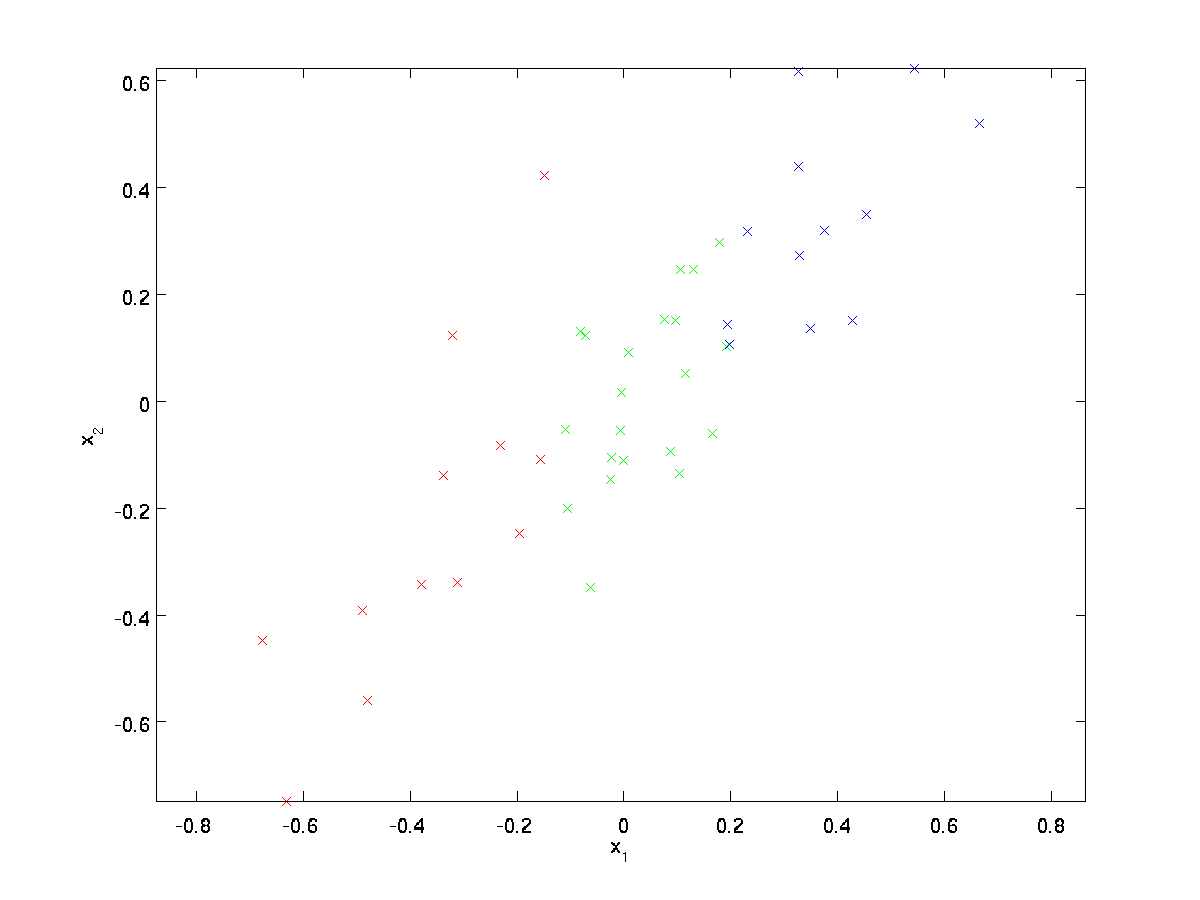
ezeket az adatokat már előre feldolgoztuk, így a \textstyle x_1 és \textstyle x_2 jellemzők átlaga (nulla) és varianciája nagyjából megegyezik.

illusztráció céljából mindegyik pontot színeztük a három szín egyikére, a \textstyle x_1 értéktől függően; ezeket a színeket az algoritmus nem használja, csak illusztráció.

a PCA talál egy alacsonyabb dimenziós alteret, amelyre kivetítheti adatainkat.
Az adatok vizuális vizsgálatából úgy tűnik, hogy \textstyle u_1 az adatok fő variációs iránya, \textstyle u_2 pedig a variáció másodlagos iránya:

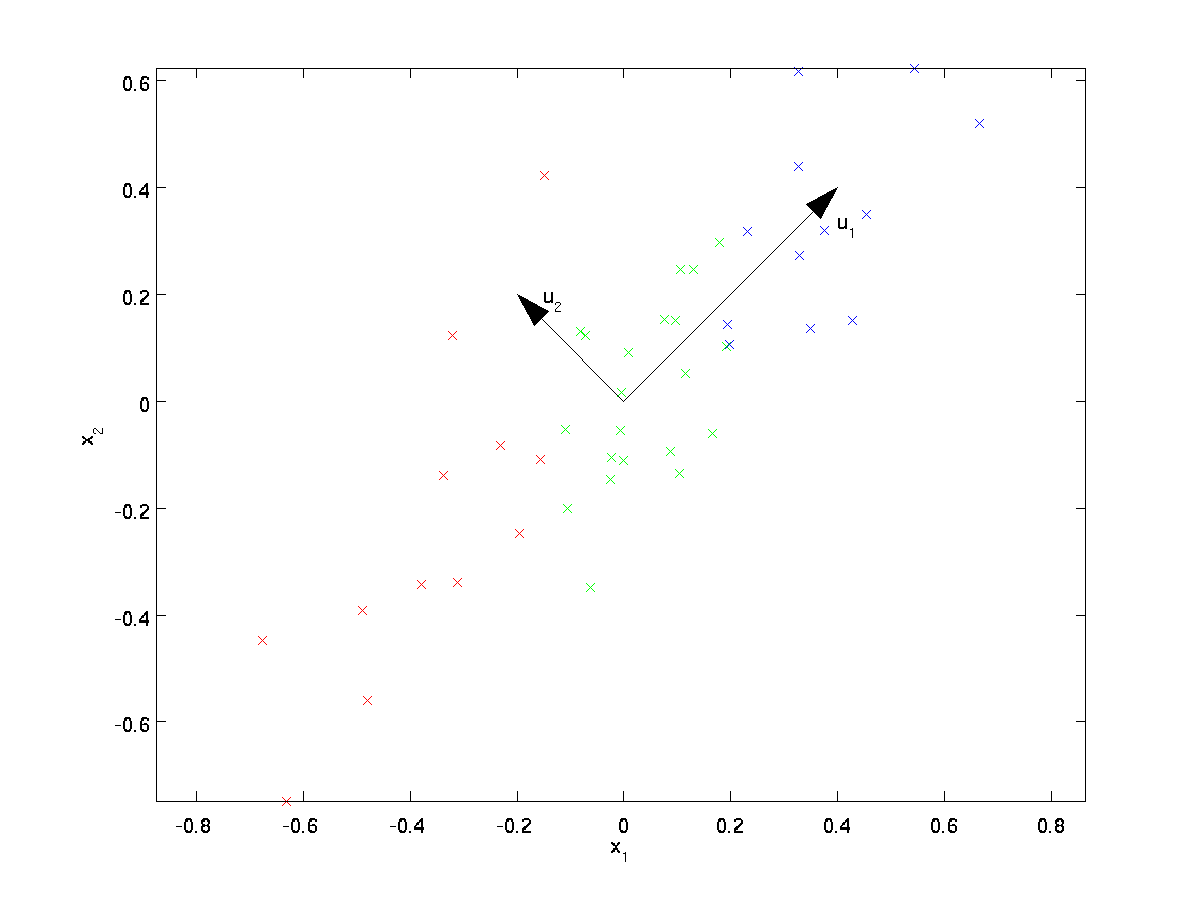
azaz az adatok sokkal inkább változnak a \textstyle u_1 irányban, mint \ textstyle u_2. A \textstyle u_1 és \textstyle u_2 irányok formálisabb megkereséséhez először a következőképpen számítjuk ki a \textstyle \Sigma mátrixot:

\ begin{align} \ Sigma = \ frac{1}{m} \ sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}

Ha a \textstyle x átlaga nulla, akkor a \textstyle \Sigma pontosan a \textstyle x kovariancia mátrixa. (a “\textstyle \Sigma” szimbólum, ejtsd: “Sigma”, a kovariancia mátrix jelölésének szokásos jelölése. Sajnos úgy néz ki, mint az összegző szimbólum, mint a \sum_{i=1}^n i; de ez két különböző dolog.)

ezután megmutatható, hogy \textstyle u_1—az adatok változásának fő iránya-a \textstyle \Sigma felső (fő) sajátvektora, \textstyle u_2 pedig a második sajátvektor.

Megjegyzés: Ha érdekli az eredmény formálisabb matematikai levezetése/igazolása, olvassa el a CS229 (Gépi tanulás) előadásjegyzeteket a PCA-ról (link az oldal alján). Nem kell ezt tennie, hogy kövesse ezt a tanfolyamot, azonban.

használhatja a szabványos numerikus lineáris algebra szoftvert, hogy megtalálja ezeket a sajátvektorokat (lásd végrehajtási Megjegyzések). Konkrétan, számoljuk ki a \ textstyle \ Sigma sajátvektorait, majd oszlopokba verem a sajátvektorokat, hogy a \textstyle U mátrixot képezzük:

\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}

Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.

a példánkban szereplő \textstyle u_1 és \textstyle u_2 Vektorok új alapot képeznek az adatok ábrázolásához. Konkrétan, legyen \ textstyle x \ in \ Re^2 néhány képzési példa. Ezután \textstyle u_1^Tx A \textstyle x vetületének hossza (nagysága) a \textstyle u_1 vektorra.

Hasonlóképpen a \ textstyle u_2^Tx A \textstyle x vektorra vetített nagysága \ textstyle u_2.

az adatok elforgatása

így reprezentálhatjuk a \textstyle x-et a \textstyle (u_1, u_2) – bázison a

\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^TX \\ u_2^TX \end{bmatrix} \end{align}

számításokkal(a “rot” index abból a megfigyelésből származik, hogy ez egy forgásnak (és esetleg visszaverődésnek) felel meg az eredeti adatok.) Vegyük a teljes képzési készlet, és kiszámítja \ textstyle x_ {\rm rot}^{(i)} = U^Tx^{(i)} minden \ textstyle i. ábrázolása ez a transzformált adatok \ textstyle x_ {\rm rot}, megkapjuk:

Ez a \textstyle u_1,\textstyle u_2 alapba elforgatott edzőkészlet. Általános esetben a \textstyle U^Tx A\textstyle u_1, \textstyle u_2,…, \ textstyle u_n alapba forgatott képzési készlet lesz.

a \ textstyle U egyik tulajdonsága, hogy” ortogonális ” mátrix, ami azt jelenti, hogy kielégíti \textstyle U^TU = UU^T = I. Tehát, ha az elforgatott \textstyle x_{\rm rot} vektorokból vissza kell térnünk az eredeti \textstyle x adathoz, akkor kiszámolhatjuk

\begin{align}x = U x_{\rm rot}, \end{align}

mert \textstyle U x_{\rm rot} = UU^T x = x.

az Adatdimenzió csökkentése

látjuk, hogy az adatok változásának fő iránya az első dimenzió \textstyle x_{\RM Rot, 1} Ennek az elforgatott adatnak. Így, ha ezeket az adatokat egy dimenzióra akarjuk csökkenteni,beállíthatjuk

\begin{align}\tilde{x}^{(i)} = x_{\rm rot, 1}^{(i)} = u_1^Tx^{(i)} \in \Re.\end{align}

általánosabban, ha \ textstyle x \ in \ Re^n és le akarjuk redukálni \textstyle k dimenziós reprezentációra \ textstyle \ tilde{x} \In \ Re^k (ahol k < n), akkor a \textstyle x_ {\RM rot} első\textstyle k összetevőit vesszük, amelyek megfelelnek a felső \textstyle k variációs irányoknak.

a PCA magyarázatának másik módja, hogy a \ textstyle x_ {\rm rot} egy \ textstyle n dimenziós vektor, ahol az első néhány komponens valószínűleg nagy (pl., példánkban azt láttuk, hogy a \ textstyle x_ {\rm rot, 1}^{(i)} = u_1^Tx^{(i)} a legtöbb példa esetében meglehetősen nagy értékeket vesz fel \textstyle i), a későbbi összetevők pedig valószínűleg kicsiek (például példánkban \textstyle x_{\rm rot, 2}^{(i)} = u_2^Tx^{(i)} valószínűleg kicsi volt). A PCA a \textstyle x_{\rm rot} későbbi (kisebb) összetevőit dobja le, és csak 0-val közelíti meg őket.konkrétan a \textstyle \tilde{x} definícióját a \textstyle x_{\rm Rot} közelítésével is elérhetjük, ahol az első \textstyle k komponens kivételével az összes nulla. Más szavakkal:

\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rothadás, 1} \\\vdots \\ x_{\rm rothadás,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\KB \begin{bmatrix} x_{\rm rothadás,1} \\\vdots \\ x_{\rm rothadás,k} \\x_{\rm rothadás,K+1} \\\vdots \\ x_{\rm Rot,n} \end{bmatrix}= x_{\rm rot} \end{align}

példánkban ez a következő \textstyle \tilde{x} ábrát adja meg nekünk (a \textstyle n=2,K=1 használatával):

mivel azonban a \textstyle \tilde{x} végső \textstyle n-k komponensei a fentiek szerint mindig nullák lennének, Nem szükséges ezeket a nullákat körül tartani, ezért a \textstyle \tilde{x}-t \textstyle k-dimenziós vektorként definiáljuk, csak az első \textstyle k (nem nulla) komponensekkel.

Ez azt is megmagyarázza, hogy miért akartuk kifejezni az adatainkat a \ textstyle u_1, u_2, \ldots, u_n basis-ben: annak eldöntése, hogy mely összetevőket tartsuk meg, csak a felső \textstyle k komponensek megtartása lesz. Amikor ezt megtesszük, azt is mondjuk, hogy “megtartjuk a felső \textstyle k PCA (vagy fő) összetevőket.”

az adatok közelítésének helyreállítása

most a \textstyle \tilde{x} \in \Re^k az eredeti \textstyle x \In \Re^n alacsonyabb dimenziós, “tömörített” ábrázolása. adott \textstyle \tilde{x}, hogyan állíthatjuk vissza a \textstyle \hat{x} közelítést a \textstyle x eredeti értékéhez? Egy korábbi szakaszból tudjuk, hogy \ textstyle x = U x_ {\rm rot}. Továbbá gondolhatunk a \ textstyle \ tilde{x}-re, mint a \textstyle x_{\rm rot} közelítésére, ahol az utolsó \textstyle n-k komponenseket nullára állítottuk. Így adott \textstyle \tilde{x} \in \Re^k, tudjuk pad ki \textstyle n-k nullák, hogy a közelítés \textstyle x_{\rm rot} \in \Re^n. végül, mi előre szorozva \textstyle U, hogy a közelítés \textstyle x. konkrétan, kapunk

\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \vége{bmatrix} = \sum_{i=1}^K u_i \tilde{x}_i. \end{align}

a fenti végső egyenlőség a \ textstyle U korábban megadott definíciójából származik. (Egy gyakorlati megvalósítás során valójában nem nulláznánk a \textstyle \tilde{x} padot, majd megszoroznánk \textstyle U-val, mivel ez sok mindent megszorozna nullákkal; ehelyett csak a \textstyle \tilde{x} \in \Re^k-t szoroznánk a \textstyle U első \textstyle k oszlopával, mint a fenti végső kifejezésben.) Ezt az adatkészletünkre alkalmazva a következő ábrát kapjuk a \textstyle \hat{x}számára:

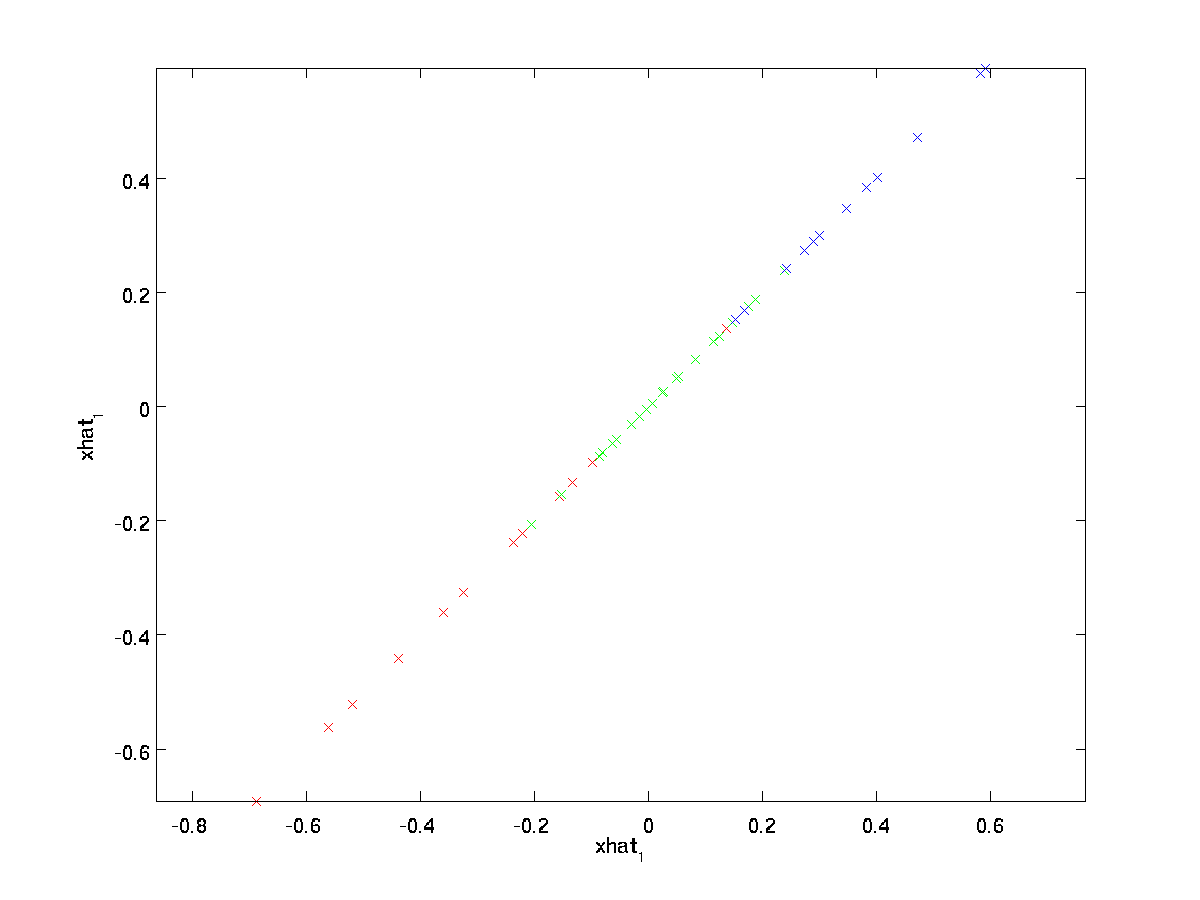
így 1 dimenziós közelítést használunk az eredeti adatkészlethez.

ha autoencodert vagy más felügyelet nélküli funkciótanulási algoritmust tanítasz, az algoritmus futási ideje a bemenet dimenziójától függ. Ha betáplálod a \textstyle \tilde{x} \In \Re^k-t a tanulási algoritmusodba a \ textstyle x helyett, akkor alacsonyabb dimenziós bemeneten fogsz edzeni, és így az algoritmusod jelentősen gyorsabban futhat. Sok adatkészletnél az alacsonyabb dimenziós \textstyle \tilde{x} ábrázolás rendkívül jó közelítés lehet az eredetihez, és a PCA ilyen módon történő használata jelentősen felgyorsíthatja az algoritmust, miközben nagyon kevés közelítési hibát vezet be.

megtartandó komponensek száma

Hogyan állítsuk be a \textstyle k-t, azaz hány PCA-komponenst kell megtartanunk? Egyszerű 2 dimenziós példánkban természetesnek tűnt, hogy 1-et megtartunk a 2 komponensből, de a magasabb dimenziós adatok esetében ez a döntés kevésbé triviális. Ha a \ textstyle k túl nagy, akkor nem fogjuk sokat tömöríteni az adatokat; a \textstyle k=n határában csak az eredeti adatokat használjuk (de más alapra forgatjuk). Ezzel szemben, ha a \ textstyle k túl kicsi, akkor lehet, hogy nagyon rossz közelítést használunk az adatokhoz.

a \textstyle k beállításának eldöntéséhez általában a \textstyle k különböző értékeire vonatkozó “‘megtartott variancia százalék”‘ értéket vesszük figyelembe. konkrétan, ha \textstyle k=n, akkor pontos közelítésünk van az adatokhoz, és azt mondjuk, hogy a variancia 100% – a megmarad. Azaz., az eredeti adatok összes variációja megmarad. Ezzel szemben, ha \ textstyle k=0, akkor az összes adatot közelítjük a nulla vektorral, így a variancia 0% – A megmarad.

általánosabban ,legyen \ textstyle \ lambda_1, \ lambda_2, \ ldots, \ lambda_n a \ textstyle \ Sigma sajátértékei (csökkenő sorrendben rendezve), úgy, hogy \textstyle \lambda_j a sajátvektor \textstyle u_j sajátértékének megfelelő sajátérték. akkor, ha megtartjuk \textstyle k fő komponenseit, a megtartott variancia százalékos arányát a:

\ begin{align} \ frac {\sum_{j=1}^k \lambda_j} {\sum_{j=1}^n \lambda_j}.\end{align}

a fenti egyszerű 2D példában \textstyle \lambda_1 = 7.29 és \textstyle \lambda_2 = 0.69. Így csak a \textstyle k=1 főkomponensek megtartásával megtartottuk a \textstyle-t 7.29/(7.29+0.69) = 0.913, vagy a variancia 91,3% – a.

a megtartott variancia százalékának formálisabb meghatározása túlmutat ezen megjegyzések hatályán. Azonban meg lehet mutatni, hogy \ textstyle \ lambda_j = \ sum_{i=1}^m x_{\rm rot,j}^2. Tehát, ha \ textstyle \ lambda_j \ approx 0, akkor ez azt mutatja, hogy \ textstyle x_ {\rm rot, j} általában 0 közelében van, és viszonylag keveset veszítünk, ha konstans 0-val közelítjük meg. Ez megmagyarázza azt is, hogy miért tartjuk meg a felső főkomponenseket (amelyek a \textstyle \lambda_j nagyobb értékeinek felelnek meg) az alsó helyett. A \ textstyle x_ {\rm rot, j} főkomponensek azok, amelyek változóbbak és nagyobb értékeket vesznek fel, és amelyeknél nagyobb közelítési hibát követnénk el, ha nullára állítanánk őket.

képek esetében az egyik általános heurisztika a \textstyle k választása, hogy megtartsa a variancia 99% – át. Más szavakkal, kiválasztjuk a \ textstyle k legkisebb értékét, amely megfelel

\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}

az alkalmazástól függően, ha hajlandó további hibát okozni, néha a 90-98% – os tartomány értékeit is használják. Amikor leírja másoknak, hogyan alkalmazta a PCA-t, azt mondani, hogy a \textstyle k-t választotta a variancia 95% – ának megtartására, szintén sokkal könnyebben értelmezhető leírás lesz, mint azt mondani, hogy megtartott 120 (vagy bármilyen más számú) összetevőt.

PCA a képeken

ahhoz, hogy a PCA működjön, általában azt akarjuk, hogy a \textstyle x_1, x_2, \ldots, x_n jellemzők értéktartománya hasonló legyen a többihez (és átlaga közel legyen a nullához). Ha korábban már használta a PCA-t más alkalmazásokban, előfordulhat, hogy külön-külön előfeldolgozta az egyes funkciókat, hogy nulla átlag és egység variancia legyen, külön megbecsülve az egyes funkciók átlagát és varianciáját \textstyle x_j. azonban ez nem az az előfeldolgozás, amelyet a legtöbb képtípusra alkalmazni fogunk. Pontosabban tegyük fel, hogy algoritmusunkat “‘természetes képek”‘ – re képezzük, így \textstyle x_j a pixel \textstyle J értéke. a “természetes képek” alatt informálisan azt a képtípust értjük, amelyet egy tipikus állat vagy személy láthat élete során.

Megjegyzés: Általában kültéri jelenetek képeit használjuk fűvel, fákkal stb., és ezekből véletlenszerűen vágjon ki kicsi (mondjuk 16×16) képfoltokat az algoritmus betanításához. De a gyakorlatban a legtöbb funkció tanulási algoritmusok rendkívül robusztus, hogy a pontos típusú kép van kiképezve, így a legtöbb kép készült egy normál kamera, mindaddig, amíg azok nem túl homályos, vagy furcsa leletek, működnie kell.

amikor a képzés a természetes képek, nincs értelme megbecsülni egy külön átlag és variancia minden pixel, mert a statisztika egyik része a kép (elméletileg) ugyanaz, mint bármely más.
Ez a tulajdonság a képek az úgynevezett “‘stationarity.”‘

részletesen, annak érdekében, hogy a PCA jól működjön, informálisan megköveteljük, hogy (i) a jellemzők átlaga megközelítőleg nulla legyen, és (ii) a különböző jellemzők eltérései hasonlóak legyenek egymáshoz. Természetes képek esetén (ii) már a variancia normalizálás nélkül is elégedett, ezért nem hajtunk végre variancia normalizálást.
(Ha a képzés audio adatok-mondjuk, a spektrogramok—vagy szöveges adatok-mondjuk, bag-of-word Vektorok-akkor általában nem végez variancia normalizálás sem.)
valójában a PCA invariáns az adatok skálázására, és ugyanazokat a sajátvektorokat adja vissza, függetlenül a bemenet skálázásától. Formálisabban, ha megszorozzuk az egyes funkcióvektorokat \ textstyle x valamilyen pozitív számmal (így minden edzéspéldában minden funkciót ugyanazzal a számmal méretezünk), a PCA kimeneti sajátvektorai nem változnak.

tehát nem fogjuk használni variancia normalizálás. Az egyetlen normalizálás, amelyet akkor végre kell hajtanunk, az átlagos normalizálás, annak biztosítása érdekében, hogy a jellemzők átlaga nulla körül legyen. Az alkalmazástól függően nagyon gyakran nem érdekel, hogy milyen fényes a teljes bemeneti kép. Az objektumfelismerési feladatokban például a kép általános fényereje nem befolyásolja a képen található objektumokat. Formálisabban nem érdekel egy képjavítás átlagos intenzitási értéke; így kivonhatjuk ezt az értéket, mint az átlagos normalizálás egyik formáját.

konkrétan, ha a \textstyle x^{(i)} \in \Re^{n} egy 16×16-os képjavítás (\textstyle n=256) (szürkeárnyalatos) intenzitási értékei, akkor az egyes képek \textstyle x^{(i)} intenzitását a következőképpen normalizálhatjuk:

\mu^{(i)} := \frac{1}{n} \sum_{j=1}^N x^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}

mindenkinek \textstyle j

vegye figyelembe, hogy a fenti két lépés külön-külön történik minden képhez \textstyle x^{(i)}, és hogy \textstyle \mu^{(i)} itt a kép átlagos intenzitása \textstyle x^{(i)}. Különösen ez nem ugyanaz, mint az egyes pixelek \textstyle x_j átlagértékének külön-külön történő becslése.

Ha az algoritmust a természetes képektől eltérő képekre oktatja (például kézzel írt karakterek képeire vagy egyetlen elszigetelt objektum képeire, amelyek fehér háttérrel vannak központosítva), akkor érdemes megfontolni a normalizálás más típusait, és a legjobb választás lehet az alkalmazásfüggő. De amikor a képzés a természetes képek, a per-kép átlagos normalizálás módszer, mint a fenti egyenletek lenne ésszerű alapértelmezett.

fehérítés

a PCA-t használtuk az adatok dimenziójának csökkentésére. Van egy szorosan kapcsolódó előfeldolgozási lépés, amelyet fehérítésnek (vagy más irodalmakban gömbölyítésnek) neveznek, amely egyes algoritmusokhoz szükséges. Ha képeken edzünk, akkor a nyers bemenet redundáns, mivel a szomszédos pixelértékek erősen korrelálnak. A fehérítés célja, hogy a bemenet kevésbé redundáns legyen; formálisabban az a vágyunk, hogy tanulási algoritmusaink olyan képzési bemenetet látjanak, ahol (i) a funkciók kevésbé korrelálnak egymással, és (ii) a funkciók mindegyike azonos varianciával rendelkezik.

2D példa

először az előző 2D példánkkal írjuk le a fehérítést. Ezután leírjuk, hogyan lehet ezt kombinálni a simítással, végül hogyan lehet ezt kombinálni a PCA-val.

hogyan tehetjük a bemeneti funkciókat korrelálatlanná egymással? Ezt már megtettük a \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} számításakor.
megismételve az előző ábránkat, a \textstyle x_{\rm rot} ábránk a következő volt:

ezen adatok kovariancia mátrixát a következő adja meg:

\begin{align}\begin{bmatrix}7.29 && 0.69\vége{bmatrix}.\end{align}

(Megjegyzés: Technikailag ebben a szakaszban a “kovarianciáról” szóló állítások közül sok csak akkor lesz igaz, ha az adatoknak nulla átlaguk van. A szakasz többi részében ezt a feltételezést implicit módon vesszük figyelembe állításainkban. Azonban, még ha az adatok átlaga nem is pontosan nulla, az itt bemutatott intuíciók továbbra is igazak, és ezért nem kell aggódnod.)

nem véletlen, hogy az átlós értékek \textstyle \lambda_1 és \textstyle \lambda_2. Továbbá az átlós bejegyzések nulla; így a \ textstyle x_ {\rm rot,1} és \textstyle x_{\rm rot, 2} korrelálatlanok, ami kielégíti a fehérített adatok egyik desideratát (hogy a jellemzők kevésbé korreláljanak).

ahhoz, hogy az egyes bemeneti funkciók egység varianciával rendelkezzenek,egyszerűen átméretezhetjük az egyes funkciókat \textstyle x_{\rm rot, i} a \textstyle 1/\sqrt{\lambda_i} értékkel. Konkrétan a fehérített adatainkat \textstyle x_{\rm PCAwhite} \In \Re^n a következőképpen definiáljuk:

\ begin{align}x_ {\rm PCAwhite, i} = \ frac{x_ {\rm rot, i} }{\sqrt{\lambda_i}}. \ end{align}

rajzolás \ textstyle x_ {\rm PCAwhite}, megkapjuk:

ezeknek az adatoknak a kovarianciája megegyezik a \textstyle I identitásmátrixéval.azt mondjuk, hogy a \textstyle x_{\rm PCAwhite} az adatok PCA fehérített változata: a \textstyle x_{\rm PCAwhite} különböző összetevői korrelálatlanok és egységvarianciájuk van.

fogfehérítés dimenziócsökkentéssel kombinálva. Ha fehérített és az eredeti bemenetnél alacsonyabb dimenziójú adatokat szeretne, opcionálisan csak a \textstyle x_ {\rm PCAwhite} felső\textstyle k összetevőit is megtarthatja. Ha a PCA fehérítést a rendszeresítéssel kombináljuk (ezt később ismertetjük), a \textstyle x_{\rm PCAwhite} utolsó néhány összetevője egyébként is majdnem nulla lesz, így biztonságosan eldobható.

ZCA Whitening

végül kiderül, hogy ez a módszer az adatok kovariancia identitáshoz \textstyle I nem egyedi. Konkrétan ,ha a \ textstyle R tetszőleges ortogonális mátrix, így kielégíti a \textstyle RR^T = R^TR = I (kevésbé formálisan, ha a \textstyle R egy rotációs/reflexiós mátrix), akkor a \textstyle R\, x_{\rm PCAwhite} identitási kovarianciával is rendelkezik.

a ZCA fogfehérítésben a \textstyle R = U-t választjuk. definiáljuk

\begin{align}x_{\rm Zcawhite} = U x_{\rm PCAwhite}\end{align}

a textstyle x_ {\rm ZCAwhite} ábrázolása, megkapjuk:

mutassuk meg, hogy a\textstyle r minden lehetséges opciója közül ez a forgatás a \textstyle x_ {\rm zcawhite} – t a lehető legközelebb hozza az eredeti bemeneti adatokhoz\textstyle x.

zca Whitening használatakor (a PCA whiteningtől eltérően) általában megtartjuk az adatok összes \textstyle N dimenzióját, és nem próbáljuk meg csökkenteni a méretét.

Regularizaton

a PCA whitening vagy a zca whitening gyakorlati megvalósításakor néha a sajátértékek \textstyle \lambda_i számszerűen közel lesznek a 0-hoz, és így a méretezési lépés, ahol osztjuk \sqrt{\lambda_i} – vel, magában foglalja a nullához közeli értékkel való elosztást; ez az adatok felrobbantását (nagy értékek felvételét) vagy más módon számszerűen instabilak lehetnek. A gyakorlatban ezért ezt a skálázási lépést kis mennyiségű szabályozással hajtjuk végre ,és hozzáadunk egy kis konstans \ textstyle \ epsilont a sajátértékekhez, mielőtt négyzetgyöküket és inverzüket vesszük:

\kezdődik{align}x_ {\rm PCAwhite,i} = \frac{x_ {\rm rot,i}} {\sqrt {\lambda_i + \ epsilon}}.\end{align}

Ha a \ textstyle x \textstyle körüli értékeket vesz fel, akkor a \textstyle \epsilon \approx 10^{-5} érték lehet jellemző.

képek esetén a \textstyle \epsilon hozzáadása itt szintén a bemeneti kép kissé simítását (vagy aluláteresztő szűrését) eredményezi. Ennek kívánatos hatása van a képpontok elrendezésének módja által okozott álnevek eltávolításában is, és javíthatja a megtanult funkciókat (a részletek túlmutatnak ezen megjegyzések hatókörén).

a ZCA whitening az adatok előfeldolgozásának egyik formája, amely \textstyle x-ről \textstyle x_{\rm ZCAwhite} – re térképezi fel. Kiderült, hogy ez egy durva modell arról is, hogy a biológiai szem (a retina) hogyan dolgozza fel a képeket. Pontosabban, ahogy a szemed érzékeli a képeket, a legtöbb szomszédos “pixel” a szemedben nagyon hasonló értékeket fog érzékelni, mivel a kép szomszédos részei általában erősen korrelálnak az intenzitással. Ezért pazarló a szemed számára, hogy minden pixelt külön-külön (a látóidegen keresztül) továbbítson az agyadba. Ehelyett a retina dekorrelációs műveletet hajt végre (ez a retina neuronjain keresztül történik, amelyek kiszámítják az “on center, off surround/off center, on surround” nevű funkciót), amely hasonló a ZCA által végrehajtotthoz. Ez a bemeneti kép kevésbé redundáns ábrázolását eredményezi, amelyet ezután továbbítanak az agyadba.

PCA Whitening végrehajtása

ebben a részben összefoglaljuk a PCA, PCA whitening és ZCA whitening algoritmusokat, és leírjuk, hogyan lehet ezeket hatékony lineáris algebra könyvtárak segítségével megvalósítani.

először is meg kell győződnünk arról, hogy az adatok (megközelítőleg) nulla átlaggal rendelkeznek. Természetes képek esetén ezt (hozzávetőlegesen) úgy érjük el, hogy kivonjuk az egyes képfoltok átlagértékét.

ezt úgy érjük el, hogy kiszámítjuk az egyes javítások átlagát, és kivonjuk az egyes javításokból. A Matlab-ban ezt a

 avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);

ezután ki kell számolnunk a \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. Ha ezt a Matlab-ban implementálja (vagy még akkor is, ha ezt C++ – ban hajtja végre, Java stb., de hozzáférjenek egy hatékony lineáris algebra könyvtárhoz), kifejezett összegként csinálni nem hatékony. Ehelyett ezt egy csapásra kiszámíthatjuk

 sigma = x * x' / size(x, 2);

(ellenőrizze a matematika helyességét.) Itt feltételezzük, hogy x egy adatszerkezet, amely oszloponként egy képzési példát tartalmaz (tehát x egy \textstyle n-by-\textstyle m mátrix).

ezután a PCA kiszámítja a \Sigma sajátvektorait. Ezt a Matlab eig funkcióval lehet megtenni. Mivel azonban a \ Sigma szimmetrikus pozitív félhatározott mátrix, számszerűen megbízhatóbb ezt az svd függvény segítségével megtenni. Konkrétan, ha

 = svd(sigma);

akkor az U mátrix tartalmazza a \Sigma sajátvektorait (oszloponként egy sajátvektor, fentről lefelé sorrendben rendezve), és az S mátrix átlós bejegyzései tartalmazzák a megfelelő sajátértékeket (szintén csökkenő sorrendben rendezve). A v mátrix egyenlő lesz U-val, és biztonságosan figyelmen kívül hagyható.

(Megjegyzés: Az svd függvény valójában kiszámítja a mátrix egyes számú vektorait és egyes számértékeit, amelyek egy szimmetrikus pozitív félhatározott mátrix speciális esetére-ami minden, amivel itt foglalkozunk—egyenlő a sajátvektoraival és sajátértékeivel. A szinguláris Vektorok vs. sajátvektorok teljes megvitatása túlmutat ezeken a megjegyzéseken.)

végül a \textstyle x_{\rm rot} és a \textstyle \tilde{x} a következőképpen számítható ki:

 xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keep

Ez adja meg az adatok PCA-ábrázolását a \textstyle \tilde{x} \in \Re^k kifejezésben. Mellékesen, ha x egy \ textstyle n-by – \ textstyle m mátrix, amely tartalmazza az összes edzésadatot, akkor ez egy vektorizált megvalósítás, és a fenti kifejezések az x_{\rm rot} és a \tilde{x} számításánál is működnek a teljes edzéskészlethez egyszerre. Az eredményül kapott x_ {\rm rot} és \ tilde{x} egy oszlopot tartalmaz, amely megfelel minden képzési példának.

a PCA fehérített adatok \textstyle x_{\rm PCAwhite} kiszámításához használja a

 xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

mivel az S átlója tartalmazza a sajátértékeket \textstyle \lambda_i, ez egy kompakt számítási módnak bizonyul \textstyle x_{\rm PCAwhite, i} = \frac{x_{\rm rot,I} }{\sqrt{\lambda_i}} egyidejűleg az összes \textstyle i.

végül a zca fehérített adatait is kiszámíthatja \textstyle x_{\rm zcawhite} a következőképpen:

 xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;