
egy mesterséges neurális hálózat (Ann) sok összekapcsolt neuronból áll:
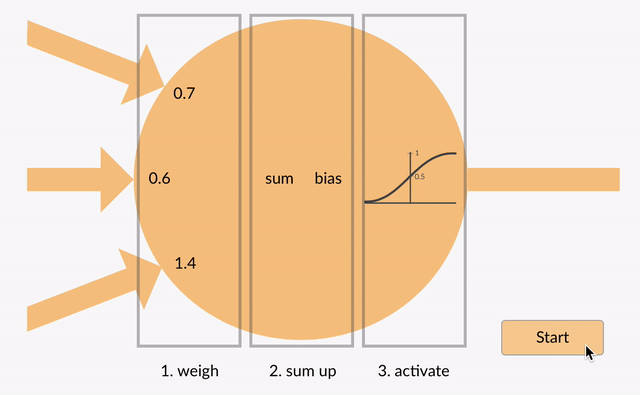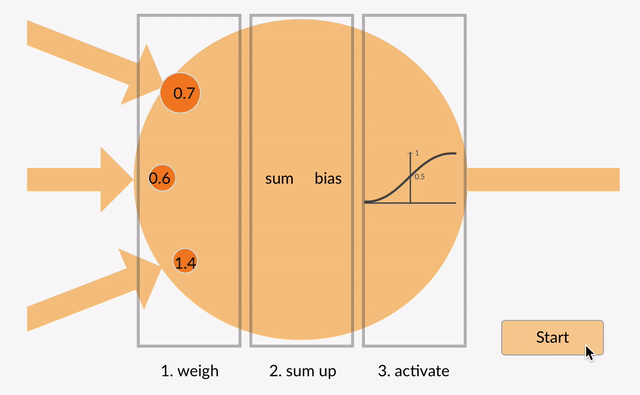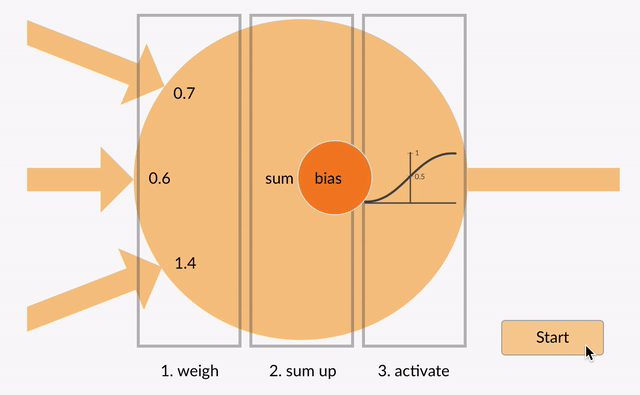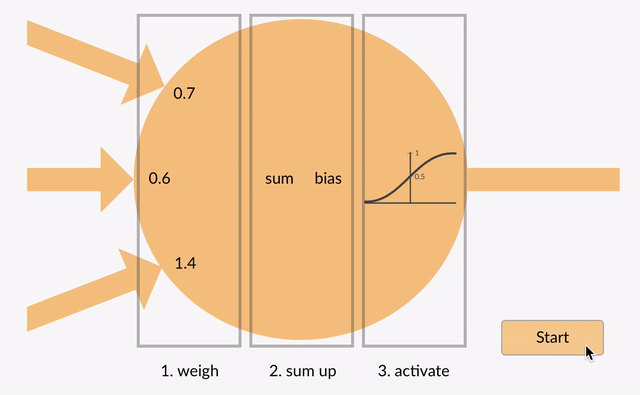
minden Neuron felvesz néhány lebegőpontos számot (például 1,0, 0,5, -1.0) és megszorozza őket más lebegőpontos számokkal (pl. 0,7, 0,6, 1,4), amelyeket súlyoknak neveznek (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). A súlyok mechanizmusként működnek, hogy összpontosítsanak, vagy figyelmen kívül hagyják, bizonyos bemenetek.

a súlyok puha kapukként működnek, hogy figyelmen kívül hagyjanak néhány funkciót (0) és összpontosítson másokra (+1), vagy akár gátolja őket (-1)
a súlyozott bemenetek ezután összeadódnak (pl. 0.7 + 0.3 + -1.4 = -0.4) egy torzítási értékkel együtt (például -0,4 + -0,1 = -0,5).
az összegzett érték (x) most átalakul kimeneti értékké (y) a neuron aktiválási funkciójának megfelelően (y = f(x)). Néhány népszerű aktiválási funkció az alábbiakban látható:

pl. -0,5 -0,05 ha a szivárgó korrigált lineáris egységet (szivárgó Relu) aktiváló funkciót használjuk: y = f(x) = f(-0,5) = max(0,1*-0,5, -0,5) = Max(-0,05, -0,5) = -0.05
A neuron kimeneti értéke (például -0,05) gyakran egy másik neuron bemenete.
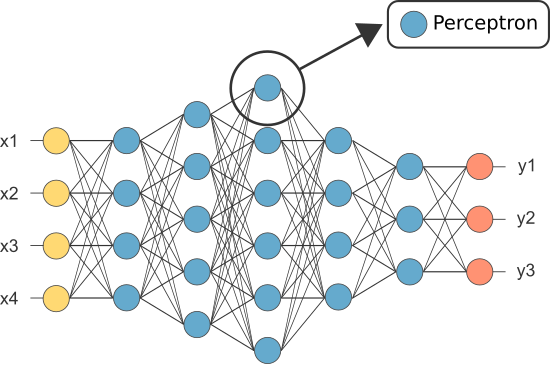
azonban az egyik első Ann-t Perceptron néven ismerték, és csak egyetlen Neuron.

a perceptron (csak) neuronjának kimenete szolgál végső előrejelzésként.

lehetővé teszi a kód saját perceptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(megjegyzés: a fenti példában nem tartalmaztunk tanulási algoritmust — a tanulási algoritmusokat egy másik oktatóanyagban fogjuk lefedni)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

akkor miért van szükségünk annyi neuronra egy ANN-ben, ha bármelyik elegendő (osztályozóként)?

sajnos az egyes idegsejtek csak lineárisan elválasztható adatokat képesek osztályozni.

az idegsejtek kombinálásával azonban lényegében egyesítjük döntési határaikat. Ezért egy sok neuronból álló ANN képes megtanulni összetett, nemlineáris döntési határokat.

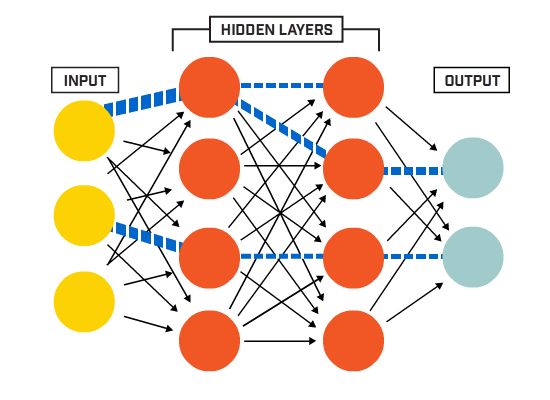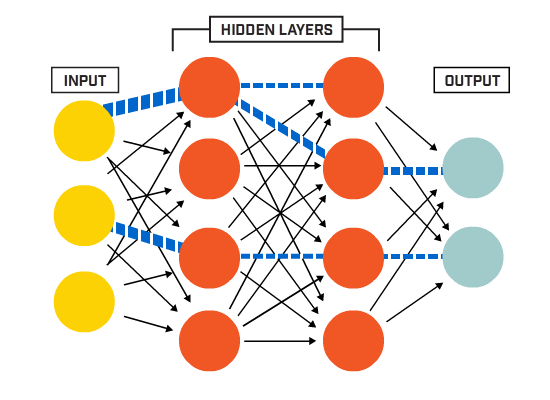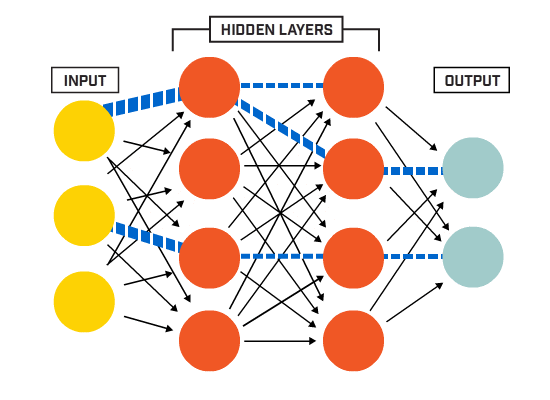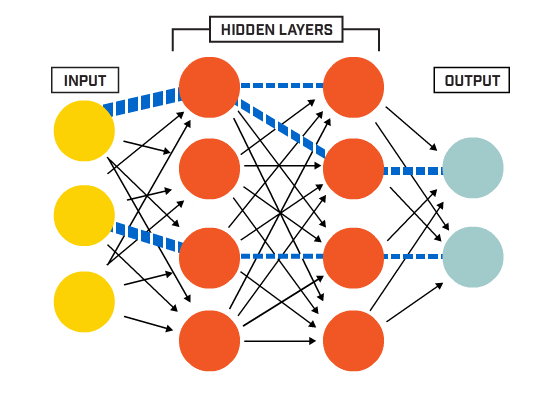
a neuronok egy adott hálózati architektúra szerint kapcsolódnak egymáshoz. Bár vannak különböző architektúrák, szinte mindegyik tartalmaz rétegeket. (NB: Az azonos rétegben lévő neuronok nem kapcsolódnak egymáshoz)
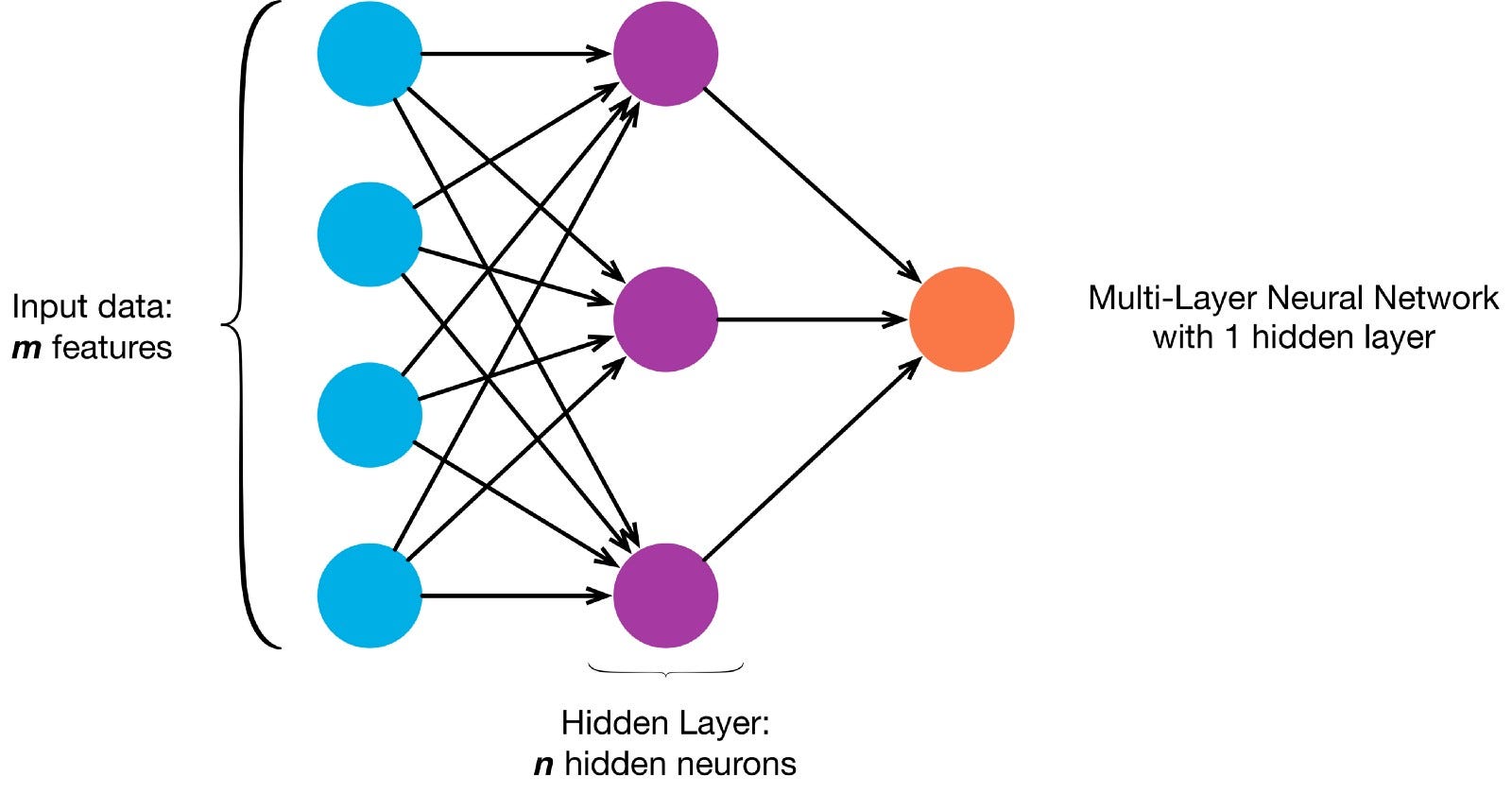
általában van egy bemeneti réteg (amely számos idegsejtet tartalmaz) egy kimeneti réteg (amely az osztályok számával megegyező számú neuront tartalmaz) és egy rejtett réteg (amely tetszőleges számú neuront tartalmaz).

egynél több rejtett réteg is lehet, amely lehetővé teszi az idegháló számára, hogy összetettebb döntési határokat tanuljon meg (bármilyen neurális hálózat az egynél több rejtett réteggel rendelkező hálót mély neurális hálónak tekintik).
lehetővé teszi, hogy építsenek egy mély NN festeni ezt a képet:

Lets download
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
most az Ann-nek a festésre való tanítása felügyelt tanulási feladat, ezért létre kell hoznunk egy címkézett képzési készletet (a képzési adatainkban minden bemenethez lesznek bemenetek és várható kimeneti címkék). A képzési bemeneteknek 2 értéke lesz (az egyes pixelek x,y koordinátái).
a kép egyszerűsége miatt ezt a problémát kétféle módon lehet megközelíteni. Osztályozási probléma (ahol az idegháló megjósolja, hogy egy pixel a “kék” vagy a “szürke” osztályba tartozik-e, tekintettel annak XY koordinátái) vagy regressziós probléma (ahol az idegháló megjósolja a pixel RGB értékeit a koordinátái alapján).
Ha ezt regressziós problémaként kezeljük: a képzési kimeneteknek 3 értéke lesz (a normalizált r,g,b értékek minden Pixelhez). – Lehetővé teszi, hogy használja ezt a módszert most.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
most hozzuk létre ANN:

- a bemeneti rétegben 2 neuronnak kell lennie (mivel 2 értéket kell bevennie: x & y koordináták).
- a kimeneti rétegben 3 neuronnak kell lennie (mivel 3 értéket kell megtanulni: r, g, b).
- a rejtett rétegek száma és az egyes rejtett rétegek neuronjainak száma két hiperparaméter, amelyekkel kísérletezni lehet (valamint a korszakok számát, amelyekre kiképezzük,az aktiválási funkciót stb.) — 10 rejtett réteget fogok használni, minden rejtett rétegben 100 neuronnal (ez egy mély neurális hálózat)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
a képzett hálózat most már megjósolhatja a normalizált rgb értékeket bármely koordinátához (a rejtett rétegek száma pl. x, y = 1,1).
ann.predict(])
array(])
segítségével az ANN megjósolni az rgb értékek minden koordináta és lehetővé teszi, hogy megjelenítse a megjósolt rgb értékek a teljes képet, hogy milyen jól sikerült (minőségileg — hagyjuk értékelési mutatók egy másik bemutató)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

próbálja meg megváltoztatni a hiperparamétereket a jobb eredmények érdekében.
Ha ahelyett, hogy ezt regressziós problémaként kezelnénk, osztályozási problémaként kezeljük, akkor a képzési kimeneteknek 2 értéke lesz (a két osztályhoz tartozó pixel valószínűségei: “kék” és “szürke”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
az ANN-t bináris osztályozóként újjáépíthetjük 2 neuronnal a bemeneti rétegben, 2 neuronnal a kimeneti rétegben és 100 neuronnal a rejtett rétegben (10 rejtett réteggel)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
most már tudjuk használni a képzett Ann megjósolni az osztály, amely minden pixel tartozik (0: “szürke” vagy 1: “Kék”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: “grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

