mi az ARIMAX modell?

mi az ARIMAX modell?

Ha elolvasta az idősorok adatainak becslésére szolgáló modellekről szóló blog oktatóanyagainkat, akkor már ismeri a 3 fő megközelítést – az autoregressziót, a mozgó átlagokat és az integrációt.

mi a közös téma ezekben a modellekben?

kizárólag egyetlen változóra támaszkodtak.

a modell azonban nemcsak a múltbeli árakat vagy a múltbeli maradványokat is figyelembe veheti.

ezek az úgynevezett “MAX” modellek, az ARMAX a nem integrált változat, az ARIMAX pedig az integrált megfelelője.

tehát ebben az oktatóanyagban meg fogjuk vizsgálni, hogy néznek ki, és megmutatjuk, hogyan lehet lépésről lépésre végrehajtani őket a Pythonban.

kezdjük, rendben?

miért nevezik az ARMAX-ot és az ARIMAX-ot “MAX” modelleknek?

az ARMAX és az ARIMAX nevek az ARMA és az ARIMA kiterjesztései. A végéhez hozzáadott X jelentése “exogén”. Más szavakkal, azt javasolja, hogy adjunk hozzá egy külön különböző külső változót az endogén változónk méréséhez.

az ARMAX és ARIMAX modell egyenlet:

mivel az egyetlen különbség az ARMAX és az ARIMAX között az, hogy az egyik integrált, a másik pedig nem, megvizsgálhatjuk az egyiket, majd kiemelhetjük, hogy a másik hogyan különbözne.

a legutóbbi blogcikkünkben (ARIMA) egy integrált modellt vizsgáltunk, tehát nézzük meg, hogy néz ki az ARIMAX egyenlete.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

persze, az egyenlet a ARMAX lenne ugyanaz, csak szeretnénk használni az általában változó, mondja O, ahelyett, hogy a delta.

Pt=C+ca+ca+ 1 Pt-1 +CA + 1 CA + 1 + o

az ARIMAX-egyenlet lebontása:

az ARIMAX-ra úgy gondolhatunk, mint az ARIMAX speciális esetére, ahol az integráció sorrendje 0.

tehát a bemutató további részében az ARIMAX-ra összpontosítunk.

és kezdjük a különböző részek lebontásával. Kezdetnek, Pt és Pt-1 képviseli az értékeket a jelenlegi időszakban és 1 időszak ezelőtt ill.

Hasonlóképpen, az Enterprises-1 és az Enterprises-1 ugyanannak a két periódusnak a hibakifejezései. Természetesen a c csak egy kiindulási állandó tényező.

a két paraméter, a 6 és az 1, azt fejezi ki, hogy a Pt-1 érték és az 1 hiba utolsó periódusának mely részei relevánsak az aktuális érték becslésében.

a modell két új kiegészítése az” X “és együtthatója, az “együttható”, azaz az “X”. Csakúgy, mint a 6, A három együtthatót a modell kiválasztása és az adatok alapján becsüljük meg. De mi van az X-szel?

mi az exogén változó?

nos, X az exogén változó, és bármilyen változó lehet, ami érdekel.

Ez lehet egy időben változó mérés, mint az inflációs ráta vagy egy másik index ára. Vagy egy kategorikus változó, amely elválasztja a hét különböző napjait. Ez a különleges ünnepi időszakok logikai elszámolása is lehet. Végül több különböző külső tényező kombinációját jelentheti.

az ötlet az, hogy bármilyen más változó vagy változó lehet, amely befolyásolhatja az árakat, mindaddig, amíg rendelkezésre állnak az adatok.

az ilyen külső tényezőket exogén változóknak nevezzük regressziónkban. Az értékeiket arra használjuk, hogy megjósoljuk és megmagyarázzuk az érdeklődésünket, ami esetünkben a jelenlegi árak.

hogyan lehet ARMAX és ARIMAX modelleket implementálni Pythonban?

kényelmesen a statsmodels csomag egy Arima nevű módszerrel érkezik, amely teljes mértékben képes kezelni az ilyen kiegészítő bemeneteket.

kezdjük a modell jellemzőinek és a modell sorrendjének megadásával:

miután ezt megtettük, meg kell adnunk az “exog”nevű exogén argumentumot is.

az átadni kívánt értéknek valamilyen tömbnek kell lennie, mivel minden időperiódushoz értékeket akarunk társítani.

például használhatjuk az S&p árakat, mint ezt az exogén változót, mivel már vannak az adatainkban.

most készen állunk egy ARIMAX (1,1,1) modell felszerelésére.

ügyeljen arra, hogy a modellváltozót úgy nevezze el, hogy az megkülönböztesse a hasonló modellektől. Ebben az esetben úgy döntünk, hogy a végén hozzáadjuk az “X, spx”-t, jelezve, hogy az exogén változó az S&P.

ezután, amint az a kivonatokból látható, ezt egyenlőnek állítjuk be az ARIMA metódussal, mint korábban, hozzáadjuk az idősort és a sorrendet, ahogy megszoktuk. Végül a kettő között beállítjuk az” exog “argumentumot” DF SPX” – vel, amely az S&P árakat jelzi.

Ha illesztjük ezt a modellt, és kinyomtatjuk az összefoglaló táblázatot, látni fogjuk, hogy kapunk egy további sort az S& P árakhoz.

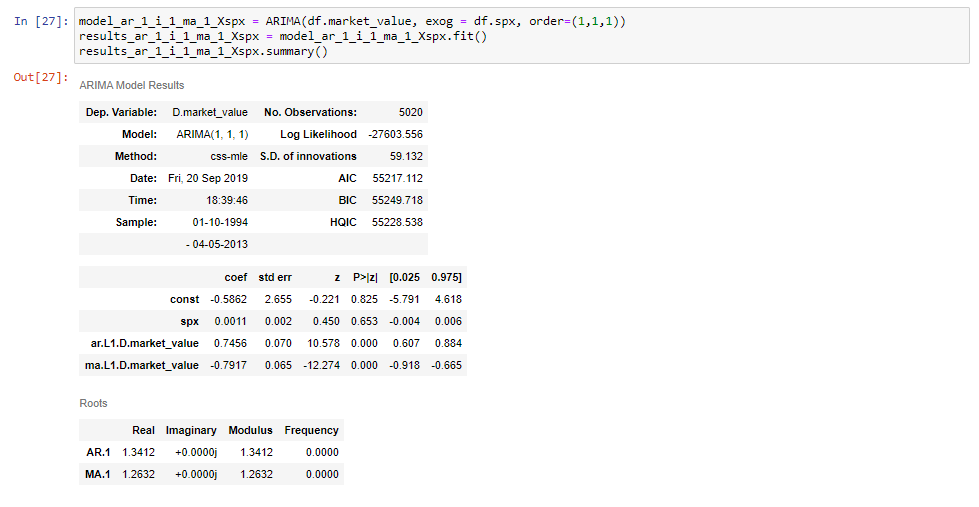
és ez minden!

sikeresen láttuk, hogyan kell végrehajtani egy ARIMAX modellt Pythonban.

Ha többet szeretne megtudni az ARIMAX-ról és más idősoros modellekről a Pythonban, győződjön meg róla, hogy nézze meg a lépésről lépésre Python oktatóanyagokat. Ha még nem ismeri a Pythont, és lelkesen szeretne többet megtudni, ez az átfogó cikk a Python programozás tanulásáról végigvezeti Önt a telepítéstől kezdve, a Python IDE-Ken, könyvtárakon és keretrendszereken keresztül a legjobb Python karrier-és álláslehetőségekig.

készen áll arra, hogy megtegye a következő lépést az adattudományi karrier felé?

nézze meg a teljes Data Science programot ma. Kezdje az alapokat a statisztikákkal, a matematikával és az Excel tanfolyamokkal. Hozzon létre egy lépésről-lépésre tapasztalat SQL, Python, R, Power BI, és Tableau. Fejlessze készségeit gépi tanulással, mély tanulással, hitelkockázat-modellezéssel, idősor-elemzéssel és Ügyfélanalitikával a Pythonban. Még mindig nem biztos benne, hogy az Adattudomány iránti érdeklődését karrierré kívánja alakítani? Az alábbi gombra kattintva felfedezheti a tantervet, vagy INGYENESEN regisztrálhat 15 órányi kezdőtől a haladó videotartalomig.