Dans la pratique de l’apprentissage machine et profond, les paramètres du modèle sont les propriétés des données d’entraînement qui apprendront seules pendant l’entraînement par le classificateur ou un autre modèle ML. Par exemple, les poids et les biais, ou les points de division dans l’arbre de décision.
Les hyperparamètres de modèle sont plutôt des propriétés qui régissent l’ensemble du processus d’entraînement. Ils comprennent des variables qui déterminent la structure du réseau (par exemple, le Nombre d’unités cachées) et les variables qui déterminent comment le réseau est formé (par exemple, le taux d’apprentissage). Les hyperparamètres modèles sont définis avant l’entraînement (avant d’optimiser les poids et le biais).
Par exemple, voici quelques variables de configuration intégrées au modèle :
- Taux d’apprentissage
- Nombre d’époques
- Couches cachées
- Unités cachées
- Fonctions d’activations
Les hyperparamètres sont importants car ils contrôlent directement le comportement de l’algo d’entraînement, ayant un impact important sur les performances du modèle en cours d’entraînement.
Le choix d’hyperparamètres appropriés joue un rôle clé dans le succès des architectures de réseaux neuronaux, compte tenu de l’impact sur le modèle appris. Par exemple, si le taux d’apprentissage est trop faible, le modèle manquera les modèles importants dans les données; inversement, s’il est élevé, il peut y avoir des collisions.
Choisir de bons hyperparamètres offre deux avantages principaux:
- Recherche efficace dans l’espace des hyperparamètres possibles; et
- Gestion plus facile d’un grand nombre d’expériences pour le réglage des hyperparamètres.
Les hyperparamètres peuvent être grossièrement divisés en 2 catégories :
1. Hyperparamètres de l’optimiseur,
2. Hyperparamètres spécifiques au modèle
Ils sont davantage liés au processus d’optimisation et de formation.
1.1. Taux d’apprentissage:
Si le taux d’apprentissage du modèle est bien trop inférieur aux valeurs optimales, il faudra beaucoup plus de temps (des centaines ou des milliers) d’époques pour atteindre un état idéal. D’un autre côté, si le taux d’apprentissage est beaucoup plus élevé que la valeur optimale, il dépasserait l’état idéal et l’algorithme pourrait ne pas converger. Un taux d’apprentissage de départ raisonnable = 0,001.
Important de considérer que:
a) le modèle aura des centaines et des milliers de paramètres chacun avec sa propre courbe d’erreur. Et le taux d’apprentissage doit tous les guider
b) les courbes d’erreur ne sont pas des formes en u propres; au lieu de cela, elles ont tendance à avoir des formes plus complexes avec des minima locaux.
1.2. Taille de Mini-Lot:
La taille du lot a un effet non trivial sur les besoins en ressources du processus de formation, la vitesse et le nombre d’itérations.
Historiquement, il y a eu un débat pour faire un entraînement stochastique où vous ajustez un seul exemple de l’ensemble de données au modèle et, en utilisant un seul exemple, effectuez une passe avant, calculez l’erreur / rétropropagate & définissez des valeurs ajustées pour tous les hyperparamètres. Et puis recommencez pour chaque exemple de l’ensemble de données.
Ou, peut-être mieux d’alimenter l’ensemble des données à l’étape d’entraînement et de calculer le gradient en utilisant l’erreur générée en regardant tous les exemples de l’ensemble de données. C’est ce qu’on appelle la formation par lots.
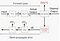
La technique couramment utilisée aujourd’hui consiste à définir une taille de mini-lot. L’entraînement stochastique est lorsque la taille du minibatch = 1, et l’entraînement par lots est lorsque la taille du mini-lot = Nombre d’exemples dans l’ensemble d’entraînement. Valeurs de départ recommandées pour l’expérimentation: 1, 2, 4, 8, 16, 32, 64, 128, 256.
Une taille de mini-lot plus grande permet des boosts de calcul qui utilisent la multiplication matricielle dans les calculs d’entraînement. Cependant, cela se fait au détriment du besoin de plus de mémoire pour le processus d’entraînement. Une taille de mini-lot plus petite induit plus de bruit dans les calculs d’erreur, souvent plus utile pour empêcher le processus d’entraînement de s’arrêter à des minima locaux. Une juste valeur pour la taille du mini-lot = 32.
Ainsi, alors que le coup de pouce informatique nous pousse à augmenter la taille du mini-lot, cet avantage algorithmique pratique incite à le réduire.
1.3. Nombre d’époques:
Pour choisir le bon nombre d’époques pour l’étape de formation, la métrique à laquelle nous devons prêter attention est l’erreur de validation.
La manière manuelle intuitive est d’avoir le train de modèle pour autant d’itérations tant que l’erreur de validation ne cesse de diminuer.
Il existe une technique qui peut être utilisée appelée Arrêt anticipé pour déterminer quand arrêter la formation du modèle; il s’agit d’arrêter le processus de formation au cas où l’erreur de validation ne s’améliorerait pas au cours des 10 ou 20 dernières époques.
2. Hyperparamètres du modèle
Ils sont plus impliqués dans la structure du modèle :
2.1. Nombre d’unités cachées:
Le nombre d’unités cachées est l’un des hyperparamètres les plus mystérieux. Rappelons que les réseaux de neurones sont des approximateurs de fonctions universels, et pour qu’ils apprennent à approximer une fonction (ou une tâche de prédiction), ils doivent avoir suffisamment de « capacité » pour apprendre la fonction. Le nombre d’unités cachées est la principale mesure de la capacité d’apprentissage du modèle.
Pour une fonction simple, il peut avoir besoin de moins d’unités cachées. Plus la fonction est complexe, plus le modèle aura besoin de capacités d’apprentissage.
Un nombre légèrement plus élevé d’unités que le nombre optimal n’est pas un problème, mais un nombre beaucoup plus grand entraînera un surajustement (c’est-à-dire que si vous fournissez un modèle avec trop de capacité, il pourrait avoir tendance à surajuster, essayant de « mémoriser » l’ensemble de données, affectant ainsi la capacité à généraliser)
2.2. Première couche cachée:
Une autre heuristique impliquant la première couche cachée est que la définition du nombre d’unités cachées plus grand que le nombre d’entrées tend à permettre de meilleurs résultats en nombre de tâches, selon l’observation empirique.
2.3. Nombre de couches:
Il arrive souvent que le réseau neuronal à 3 couches surpasse un réseau à 2 couches. Mais aller encore plus loin aide rarement beaucoup plus. (exception sont les réseaux de neurones convolutifs, où plus ils sont profonds, meilleurs ils fonctionnent).
Techniques d’optimisation des hyperparamètres
Le processus de recherche des hyperparamètres les plus optimaux dans l’apprentissage automatique est appelé optimisation des hyperparamètres.
Les algorithmes courants incluent :
- Recherche par grille
- Recherche aléatoire
- Optimisation bayésienne
Recherche par grille
La recherche par grille est une technique traditionnelle pour implémenter des hyperparamètres. Il s’agit un peu de la force brute de toutes les combinaisons. La recherche de grille nécessite la création de deux ensembles d’hyperparamètres:
- Taux d’apprentissage
- Nombre de couches
La recherche par grille entraîne l’algorithme pour toutes les combinaisons en utilisant les deux ensembles d’hyperparamètres (taux d’apprentissage et nombre de couches) et mesure les performances en utilisant la technique de validation croisée. Cette technique de validation garantit que le modèle entraîné obtient la plupart des modèles de l’ensemble de données (l’une des meilleures méthodes pour effectuer la validation en utilisant la « validation croisée K-Fold » qui aide à fournir de nombreuses données pour la formation du modèle et de nombreuses données pour les validations).
La méthode de recherche par grille est un algorithme plus simple à utiliser, mais elle souffre si les données ont un espace dimensionnel élevé appelé la malédiction de la dimensionnalité.
Random Search
Échantillonne aléatoirement l’espace de recherche et évalue les ensembles à partir d’une distribution de probabilité spécifiée. Au lieu d’essayer de vérifier les 100 000 échantillons, par exemple, nous pouvons vérifier 1 000 paramètres aléatoires.
L’inconvénient de l’utilisation de l’algorithme de recherche aléatoire, cependant, est qu’il n’utilise pas les informations des expériences précédentes pour sélectionner l’ensemble suivant. De plus, il est difficile de prédire la prochaine expérience.

Optimisation bayésienne
Le réglage de l’hyperparamètre maximise les performances du modèle sur un ensemble de validation. Les algos ML nécessitent fréquemment un réglage fin des hyperparamètres du modèle. Malheureusement, cet accord est souvent appelé « fonction noire » car il ne peut pas être écrit dans une formule (les dérivées de la fonction sont inconnues).
Un moyen plus attrayant d’optimiser &Pour affiner les hyperparamètres, il faut activer une approche automatisée de réglage du modèle, par exemple en utilisant l’optimisation bayésienne. Le modèle utilisé pour approximer la fonction objectif est appelé modèle de substitution. Un modèle de substitution populaire pour l’optimisation bayésienne est le processus gaussien (GP). L’optimisation bayésienne fonctionne généralement en supposant que la fonction inconnue a été échantillonnée à partir d’un processus gaussien (GP) et maintient une distribution postérieure pour cette fonction au fur et à mesure des observations.
Il y a deux choix majeurs à faire lors de l’optimisation bayésienne:
- Sélectionnez des fonctions précédentes qui exprimeront des hypothèses sur la fonction à optimiser. Pour cela, nous choisissons le processus Gaussien au préalable ;
- Ensuite, nous devons choisir une fonction d’acquisition qui est utilisée pour construire une fonction d’utilité à partir du modèle postérieur, ce qui nous permet de déterminer le point suivant à évaluer.
Processus gaussien
Un processus gaussien définit la distribution antérieure sur les fonctions qui peut être convertie en une fonction postérieure sur les fonctions une fois que nous avons vu certaines données. Le processus gaussien utilise une matrice de covariance pour s’assurer que les valeurs sont proches les unes des autres. La matrice de covariance ainsi qu’une fonction µ moyenne pour produire la valeur attendue ƒ(x) définissent un processus gaussien.
1. Le processus gaussien sera utilisé comme préalable pour l’inférence bayésienne;
2. Le calcul du postérieur permet de l’utiliser pour faire des prédictions pour des cas de test invisibles.

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. Les fonctions d’acquisition populaires sont
- Probabilité Maximale d’Amélioration (MPI)
- Amélioration attendue (EI)
- Limite de confiance supérieure (UCB)
L’Amélioration attendue (EI) est populaire et définie comme :
EI(x) =𝔼
où ƒ(x) est l’ensemble optimal actuel d’hyperparamètres. Maximiser les hyperparamètres améliorera ƒ.
