ICM Poker: Le Seul Guide Dont Vous Avez Besoin

Au poker, ICM signifie « Modèle de Puce indépendant ». Il aide un joueur de poker à n’importe quelle étape d’un tournoi de poker à déterminer son équité de tournoi actuelle. (Combien d’argent dans la cagnotte devrait actuellement leur appartenir.)

Le calcul est basé sur le nombre de jetons qu’ils ont actuellement par rapport au nombre total de jetons en jeu et à la structure de paiement.

Ces informations peuvent être utilisées pour –

• Aider les joueurs dans les décisions qu’ils doivent prendre pendant une main pendant un tournoi, en particulier lorsqu’ils se dirigent vers les étapes de la table finale ou ultérieure.
• Aide à déterminer la répartition de la cagnotte si un « coup » est convenu avant la fin d’un tournoi.

Table des Matières

GRAPHIQUE ICM – Quels Facteurs Sont Pris en Compte?

ICM * ne* considère:	ICM * ne* considère pas:	ICM * ne* considère pas:
Player’s total size of chip stack	Size of blinds / Stack sizes in blinds
Total # of chips in play	Length of levels
Number of Entrants	Player Skill
Payout structure	Table position
Nombre de joueurs restants	Taille du tournoi

LES BASES – Comment fonctionne l’ICM au Poker?

La raison de l’utilisation de l’ICM dans le poker de tournoi est que la valeur de chaque jeton de tournoi varie à mesure que chaque joueur est éliminé et / ou que les paiements continuent d’augmenter. Cette situation est assez différente des cash games, où chaque montant de jetons est fixe et représentatif du montant en dollars correspondant.

Dans un cash game, si vous doublez, vous doublez votre capital, doublez votre pile et doublez votre argent. Dans un tournoi, vous pouvez doubler dès la première main, mais vous n’avez toujours pas doublé votre capital de tournoi.

Pour utiliser un exemple simplifié pour aider à montrer cela, supposons que nous ayons un SNG de 10 joueurs avec des paiements standard: le 1er obtient 50%, le 2e 30% et le 3e 20%. Tous les joueurs reçoivent 1 000 jetons de tournoi, ce qui signifie qu’il y a 10 000 jetons au total en jeu.

Avant le début du tournoi, ICM nous indique que (tous les joueurs ayant des piles de départ égales) tous les joueurs ont le même EV dans le tournoi de 10%. (Rappelez-vous que l’ICM ne prend pas les compétences, la position de la table, les stores, etc. en considération. Il s’agit simplement de prendre le nombre de jetons qu’un joueur a et de le relier à la quantité en jeu.)

Sur la toute première main de ce tournoi hypothétique, le Joueur 1 double (assis dans la grosse blind) et le Joueur 10 bustes (qui était assis dans la petite blind). Par conséquent, le joueur 1 a maintenant 2 000 jetons, et tout le monde en a encore 1 000.

Le joueur 1 détient maintenant 20% des jetons en jeu, mais a-t-il doublé son capital de tournoi par rapport à ses 10% d’origine ?

Non. Pourquoi est-ce le cas?

En raison de la structure différente de la cagnotte, le doublement des jetons ne doublera pas automatiquement EV. S’il s’agissait d’un événement gagnant-gagnant, avec 20% des jetons maintenant en jeu, le joueur 1 aurait un tir de 20% pour gagner 100% de la cagnotte. Par conséquent, son capital de tournoi serait de 20%.

Cependant, dans ce tournoi, la cagnotte est également divisée entre la 2e et la 3e place. Par conséquent, le mieux que tout joueur puisse faire est de gagner un maximum de 50% d’équité totale dans le tournoi 5 50% de la cagnotte totale. Ils ont également une chance de remporter peut-être 30% ou 20% du capital du tournoi, s’ils se classent 2e ou 3e. C’est pour ces placements supplémentaires qu’ICM est utilisé pour calculer une représentation plus précise de l’équité d’un tournoi.

En utilisant une calculatrice ICM, nous pouvons voir que l’équité du tournoi du joueur 1 est maintenant à 18,44%. Par conséquent, bien que le doublement de sa pile ait considérablement augmenté ses fonds propres dans le tournoi de 10% à 18,44%, il n’a pas complètement doublé ces fonds propres.

Pourquoi est-ce, et où sont allés les capitaux propres restants?

Les huit autres joueurs restants ont reçu l’équité supplémentaire du tournoi, gagnant 0,19% de l’équité du joueur 10. Et ils n’ont même pas joué une main! Cette augmentation des fonds propres est logique, car il y a maintenant UN joueur de moins à affronter avec la même quantité de jetons en jeu.

REMARQUE: Les montants de paiement utilisés pour chaque place ITM affecteront également ICM et le calcul des actions du tournoi. S’il s’agissait d’une configuration 1ère – 2ème – 3ème avec des gains de 65% -25% -10% du prize pool total, l’équité du joueur 1 aurait bondi à précisément 19% en répétant ce même scénario!

PLUS DE BASES DE L’ICM: Calcul de l’ICM (Simple)

Pour illustrer davantage pourquoi doubler sa pile de jetons ne double pas son équité en tournoi (et aussi pour aider à mieux comprendre le concept de l’ICM dans le poker en tournoi), considérez ceci:

Deux joueurs restent dans un SNG à 6 joueurs, où chaque joueur a commencé avec 1 000 jetons. Les paiements sont de 70% pour le 1er et de 30% pour le 2e. Le joueur 1 a une avance massive de jetons avec 5 900 jetons. Le joueur 2 a une maigre pile de 100 jetons. Après une main, le joueur 2 parvient à doubler ses jetons, ce qui signifie que les tailles de pile sont maintenant de 5 800 et 200.

L’équité du tournoi du joueur 2 a-t-elle doublé en doublant son stack ?

Non, non, ce n’est pas le cas.

Avec seulement deux joueurs restants, chaque joueur est GARANTI 30% de la cagnotte. Ce pourcentage représente le pire résultat que chaque joueur pourrait obtenir s’il perdait le tournoi.

Par conséquent, les joueurs avec des jetons restants auront quelque part plus de 30% d’équité dans le tournoi. En tant que tels, les deux joueurs restants dans cet exemple seraient en compétition pour les 40% restants de la cagnotte. (Oui, le montant total pour le 1er est de 70% de la cagnotte, mais comme chaque joueur a au moins 30% verrouillé, le solde du tournoi reste à gagner. Et, la différence entre la 1ère (70%) et la 2ème place (30%) est de 40%.)

Tant que le joueur 2 a encore des jetons, il y a une petite chance qu’il puisse revenir et gagner. H a une petite partie des capitaux propres dans les 40% restants.

Par conséquent, avec seulement 100 jetons, le joueur 2 aurait une équité de tournoi de 30,67%. Nous arrivons à ce chiffre en prenant l’équité de base qu’il a déjà obtenue (30%) et en ajoutant cela à sa probabilité (basée simplement sur le nombre de jetons dans sa pile par rapport au nombre total en jeu) de gagner les 40% d’équité restants:

= 30% d’équité garantie + ((100 jetons / 6 000 jetons au total) * 40% de tournoi restant)

= 0.3 + (0.0167 * 0.4)
=0,3 + 0,0067
= 0,3067

Comment Calculer l’ICM Au Poker

Comme vous pouvez le voir, doubler sa pile dans un tournoi de poker ne double pas son capital. Il est essentiel de savoir calculer l’ICM, afin que vous puissiez prendre les décisions correspondantes de manière stratégique, de main en main. (Voir les sections suivantes de cet article.)

Aussi, afin que vous sachiez combien chaque joueur devrait obtenir si une situation de « hachage » se présentait à la table finale. Cependant, contrairement à la section précédente avec les joueurs heads-up, les calculs seront un peu plus compliqués avec plus de joueurs ajoutés au mix.

La façon dont nous calculons l’ICM manuellement dans un scénario avec plusieurs (3+) joueurs restants dans un tournoi est la suivante. Nous prenons le nombre de jetons dont dispose un joueur (par rapport au nombre total de jetons en jeu) et l’utilisons pour calculer la probabilité que ledit joueur se place dans chaque place restante d’un tournoi.

Après cela, nous relions ces pourcentages aux prix monétaires correspondants associés à chaque place, puis additionnons les résultats de tous les résultats ensemble.

Utilisons une situation réelle avec les joueurs et leur nombre de jetons pris depuis le début du Jour 9 (jeu à 3 mains) lors du Main Event des WSOP 2019 à Las Vegas:

• Hossein Ensan – 326 800 000 (63,5% de jetons en jeu)
• Dario Sammartino – 67 600 000 (13,1% de jetons en jeu)
• Alex Livingston – 120 400 000 (23,4% de jetons en jeu)

Total de jetons en jeu: 514 800 000

REMARQUE: Bien qu’un chop n’ait jamais eu lieu dans ce tournoi, les calculs suivants sont présentés pour illustrer comment effectuer des calculs ICM manuels pour un chop multijoueur.

Avec trois joueurs restants, il y avait six possibilités de conclure le tournoi.

Ces possibilités seront listées ici par ordre de 1ère, 2ème et 3ème place:

1)Ensan, Sammartino, Livingston
2)Ensan, Livingston, Sammartino
3)Livingston, Ensan, Sammartino
4) Sammartino, Ensan, Livingston
5) Livingston, Sammartino, Ensan
6) Sammartino, Livingston, Ensan

Pour nos calculs ICM, supposons que nous essayons de trouver l’équité du tournoi ICM pour Hossein Ensan, le leader de la puce du jour 9. Vous remarquerez que Ens dans le tableau ci-dessus Ens l’Ensan avait deux possibilités pour se placer 1ère, deux pour se placer 2ème et deux chances pour se placer 3ème.

Pour nous aider à convertir tout cela en équité de tournoi ICM, nous devrons déterminer la probabilité qu’il termine le tournoi à chaque place (en fonction de la taille actuelle de la pile de jetons).

Probabilité de placer le 1er Options Options 1 + 2

Avec Ensan ayant 63,5% des jetons en jeu, il y a 63,5% de chances qu’il obtienne le 1er, basé strictement sur la prise de son nombre actuel de jetons par rapport au montant total du jeu.

Probabilité de Placer 2ème OptionsOptions 3 + 4

Pour cette section, nous devrons calculer les options séparément, pour tenir compte des probabilités des deux autres joueurs de se placer 1er devant lui.

Pour l’option 3, Livingston a 23,4% de chances d’arriver en 1ère place. Pour déterminer la probabilité que l’Ensan arrive ensuite 2ème (entre lui et Sammartino), il faut prendre (les jetons de l’Ensan / jetons des joueurs restants — dans ce cas, ceux de l’Ensan + ceux de Sammartino).

Cette formule nous donne la réponse de (326,800,000 / (326,800,000 + 67,600,000) = 82.9%, ce qui signifie qu’il y a un 82.9% de chances qu’Esan arrive 2ème, si Livingston se place 1ère.

Pour déterminer la probabilité totale de cette option, il faut maintenant multiplier ces deux possibilités ensemble (Livingston gagnant et Ensan arrivant 2ème): 0.234 * 0.829 = 0.194 = 19.4% chance que ce scénario se produise.

Pour l’option 4 du tableau, nous faisons les mêmes calculs, mais avec Sammartino qui arrive 1er (13,1% de chance). En utilisant la même formule mathématique (13,1% x (328,8 millions / 447,2 millions), nous constatons que ce résultat a 9,6% de chances de se produire, sur la base des piles ICM et chip.

En additionnant les probabilités de chaque scénario (19,4% et 9,6%), on voit qu’il y a 29% de chances que l’Ensan arrive en 2ème place.

Probabilité de placer la 3ème Options Options 5 + 6

La probabilité résultante de voir l’Ensan arriver 3ème serait de 7,5%. Nous arrivons à ce nombre en découvrant qu’il y a 4% de survenance de l’option 5 (23,4% * (67,6 millions / 394,4 millions)) et une probabilité de 3,5% de survenance de l’Option 6 (13,1% * (120,4 millions / 447,2 millions)).

En convertissant % en IC En utilisant ICM

En utilisant ces pourcentages, nous pouvons ensuite calculer l’EV qu’un joueur a actuellement en $$$ dans un tournoi, ce qui est précisément ce qui serait utilisé pour calculer les gains, si une situation à « couper » se présentait.

Ainsi, en reprenant notre exemple, voici le Top 3 des paiements des prix ont été pour l’2019 main Event des WSOP:

• 1er – de 10 000 000 $
• 2ème – $6 000 000 d’
• 3ème – 4 000 000 de dollars

Voici le $EV Ensan a pour la finition dans chaque lieu:

• EV de 1er = 0.635 x de 10 000 000 $ = $6,350,000
• EV de 2e = 0.290 x $à 6 000 000 = $1,740,000
• EV de 3e = 0.075 x de 4 000 000 $ = $à 300 000 $

La Dernière Étape : Calculer Son Équité avec Plusieurs Joueurs Restants

Formule ICM pour le calcul de l’ICM

Pour résumer la section précédente sur le calcul de l’ICM, voici la formule étape par étape à utiliser pour calculer votre équité de tournoi en fonction des considérations ICM:

1. Déterminez la taille en jetons de la pile de jetons de chaque joueur

1. Reliez cela au nombre total de jetons en jeu –

• Pile de jetons / Total de jetons
• Ce calcul montrera les chances de chaque joueur de GAGNER le tournoi.

1. Déterminez la probabilité de toutes les différentes possibilités pour la fin du tournoi (en termes de place que chaque joueur pourrait obtenir) –

• Déterminez tous les différents résultats possibles.
• Déterminez la probabilité de chaque résultat en commençant par la probabilité que le gagnant de chaque scénario obtienne la 1ère place.
• Après cela, pour déterminer la probabilité de la 2e place, les possibilités de gagner de multiples gagnants (leur part de jetons) par (jetons de la 2e place / total des autres jetons restants, y compris la 2e place).
• Pour faire cette formule pour plus de trois joueurs, vous devez combiner la probabilité de 1ère et 2ème place (etc.) avant de calculer pour un joueur dans une position ultérieure.

1. Reliez ces actions au montant en $ associé aux places payées pour déterminer EV-

Logiciel ICM pour les calculs ICM

Comme le montre l’exemple ci-dessus, même avec seulement trois joueurs restants dans un tournoi, la quantité de calculs ICM à effectuer pour calculer EV est déjà assez longue. (Et à ce moment-là, nous calculions l’EV / ICM pour un seul joueur sur les trois en question!)

Imaginez faire ces calculs si le jeu était à 4 mains ou à 5 mains, ou juste après que les joueurs aient touché l’argent! Le nombre de combinaisons pour la façon dont chaque joueur finirait par prendre énormément de temps s’il était fait manuellement.

Par conséquent, en raison de la longueur et de la complexité de ces calculs, il n’est pas rare que les joueurs / salles de poker utilisent des logiciels ICM et des calculatrices ICM – en particulier dans le cas où les joueurs cherchent à couper.

Considérations sur le gameplay de l’ICM: Tailles de pile et pression de l’ICM

En ce qui concerne l’ICM d’un point de vue plus stratégique / gameplay maintenant, la pression de l’ICM peut prendre de nombreuses formes et diverses situations. Principalement, ce terme fait référence aux restrictions et modifications qu’un joueur doit apporter à ses gammes de mains et / ou à la façon dont il joue des mains spécifiques. Les joueurs ne veulent pas perdre de grandes quantités d’équité dans un tournoi s’ils peuvent l’éviter, en raison de l’ICM et des implications de paiement.

Comme exemple typique, jetez un coup d’œil à une situation courante qui se produit lorsque l’ITM (dans l’argent) dans les SNG. Habituellement, il y a toujours un joueur avec chacune des piles suivantes: 1 grande pile, 1 pile moyenne et 1 pile courte.

Pour les besoins de l’exemple ci-dessous, supposons que les joueurs ont des tailles de pile de 3 000, 6 000 et 9 000 jetons.

La façon dont ces différentes tailles de pile devraient par la suite se relier et s’ajuster en raison de la pression et des considérations ICM est assez simple:

1. En tant que pile moyenne, vous ne voulez pas entrer dans des confrontations épiques avec la grosse pile car cela pourrait vous coûter des capitaux propres et / ou votre vie de tournoi. Vous préféreriez voir le short stack éclater en premier (augmentant par la suite votre capital de tournoi) avant de vous impliquer trop fortement dans un gros pot avec le big stack. Dans le même temps, la pile moyenne peut prendre * quelques* risques contre la pile courte, mais doit toujours faire preuve de prudence. Bien qu’il ne perde pas et ne perde pas toute son équité dans le tournoi s’il perd un all-in au short stack, cela le laisserait probablement sur les cordes, devenant le short stack.

1. Pour la raison ci-dessus, en tant que grosse pile, vous pouvez appliquer une grande pression à la fois sur la pile moyenne ET sur la pile courte, mais surtout sur la pile moyenne. Il est menotté entre vous et le short stack. Il préférerait préserver son équité de tournoi et potentiellement en gagner si vous êtes en mesure de casser la pile la plus courte. Et, alors que le court stack * pourrait * mettre une petite brèche dans votre stack, même après qu’ils doublent à travers vous, vous auriez toujours des capitaux propres considérables dans le tournoi.

Considérations de gameplay ICM: La Bulle

Ces concepts de « taille relative de la pile » ne s’appliquent pas seulement lorsqu’il reste trois personnes; ils peuvent également s’appliquer à toute la table finale d’un MTT (car il y a généralement un saut de salaire pour chaque élimination), ainsi que lorsque la « bulle d’argent » est sur le point d’éclater.

La bulle est une partie unique d’un tournoi de poker. Terminez de l’argent, et vous avez perdu toute l’équité du tournoi (et n’avez rien à montrer pour cela). Naviguez au-delà de la bulle et non seulement vous pouvez continuer à jouer, mais vous avez également un montant minimum d’équité de tournoi verrouillé, ce qui aura par la suite un beau jour de paie rentable pour l’accompagner!

Les considérations ICM sont très répandues pendant la bulle dans un tournoi de poker. En tant que tel, les piles courtes pendant cette période cherchent généralement à éviter toute confrontation et à ne pas faire faillite.

ICM Catastrophe: Un exemple de main

Une main intense de la table finale des World Series of Poker 2010: Main Event montre l’importance des considérations ICM et à quel point elles peuvent nuire considérablement aux résultats des tournois.

Pour préparer le terrain, avec trois joueurs restants, voici les comptes de jetons avant le début de la catastrophe d’une main:

• John Racener – 36 450 000 (17% des jetons restants)
• Jonathan Duhamel – 88 100 000 (40% des jetons restants)
• Joseph Cheong – 95 050 000 (43% des jetons restants)

John Racener a plié le bouton. Joseph Cheong a augmenté à 2,9 millions de la petite blind avec As7h. Duhamel 3bet à 6,75 millions avec QcQd. Cheong 4bet à 14,25 millions. Duhamel 5bet à 22,75 millions.

Et ensuite… Cheong 6-bet l’a ARRACHÉ pour 95,05 millions, ayant couvert Duhamel!

Avant d’arriver aux résultats de la main, plongeons brièvement dans l’analyse de la décision de Cheong de 6bet jam A7o:

• Cheong a un As dans la main, ce qui permet de réduire le nombre d’As que Duhamel pourrait avoir. (Les combinaisons possibles d’AK ou d’AQ se réduisent de 16 à 12. Cela réduit également de moitié le nombre de combos d’As de poche que Duhamel pourrait avoir de 6 à 3.)
• Cheong a une légère avance sur Duhamel, ce qui est sans aucun doute significatif. Alors que les deux joueurs ont à peu près la même équité de tournoi actuellement, si les deux joueurs font le all-in et que Duhamel perd, alors c’est un gros problème. Principalement en raison de la taille actuelle de la pile de Racener par rapport aux deux, ainsi que de l’équité subséquente qu’il perdrait à Racener en cassant.

En bref, Cheong a placé Duhamel dans un endroit fascinant et très sous pression. Oui, bien qu’il y ait probablement une meilleure sélection de mains de HACHE avec lesquelles Cheong aurait finalement pu décider de bluffer 6bet (combinaisons adaptées ou roues / connectées), cela met sans aucun doute Duhamel à l’épreuve, surtout lorsque vous y tenez compte des considérations ICM (que Duhamel pourrait se ranger derrière Racener, s’il appelle all-in et perd).

Cela dit, à long terme, est-ce que 6bet pousse A7o à cet endroit a + EV play? Probablement pas. (Nous devrions disséquer abondamment les fourchettes de mains, les actions de mains et les actions de tournois pour ce faire.) Mais, en pensant à long terme, ce jeu a peut-être coûté des millions de dollars en capitaux propres à Cheong.

Considérations de gameplay ICM:Stratégie et théorie

Dans les cash games, si vous faites face à une place tout-en-un, pour montrer un profit à long terme, vous devriez:

• Calculez vos cotes de pot et l’équité dont vous avez besoin pour gagner la main pour faire un appel rentable.
• Déterminez l’équité réelle de votre main par rapport à une fourchette approximative de votre adversaire.
• Faites l’appel si vous avez les cotes appropriées (+ appel chipEV) OU pliez si vous avez des cotes / capitaux propres insuffisants pour le spot en question.

Pour les situations de tournoi, cependant, ce n’est pas toujours aussi sec à cause de (vous l’avez deviné!) Considérations liées à la GIC.

À titre d’exemple, disons que nous sommes sur la bulle d’un SNG à 9 mains (il reste 4 joueurs). Tout le monde a des piles égales de 4 500. Les stores sont de 200/400, et il y a aussi un ante 25. Le CO se plie, le BTN s’all-in, le SB se plie, et nous regardons QJs dans le BB.

1. Est-ce un appel basé sur ICM (le joueur suivant aux bustes part sans rien; tout le monde gagne de l’argent)?
2. Combien d’actions sont gagnées / perdues en appelant ici?

Tout d’abord, il faut supposer la portée de poussée du bouton, qui pourrait très bien ressembler à ceci (42,87% des mains):

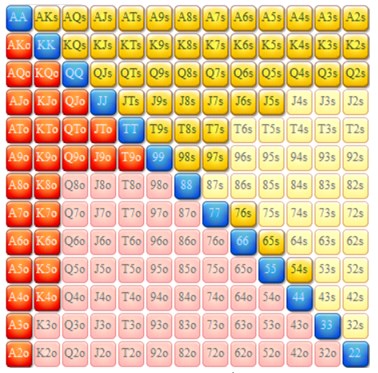
22+, A2+, K2s+, K4o +, Q2s +, Q9o +, J5s+, J9o+, T7s+, T9o, 97s+, 76s, 65s, 54s

Par rapport à cette plage, nous pouvons utiliser un calculateur d’équité pour déterminer que QJs a 47,69 % d’équité pour gagner la main, 3,10% pour égaler et 49,21% d’équité pour perdre la main par rapport à cette fourchette. Avec notre grosse blind et notre ante déjà au milieu, nous devions annuler 4 075 jetons de plus pour gagner les 5 175 jetons au milieu (petite blind + grosse blind + antes + poussée du méchant).

Dans un cash game, nous déterminerions simplement, via les cotes du pot, que nous aurions besoin de 44,05% d’actions pour appeler. Contre la plage présumée de poussée de bouton de notre adversaire, notre capital total (y compris les possibilités d’égalité) de 49,24% semble se porter plutôt bien, ce qui signifie que nous devrions appeler…si c’était un cash game !

Comme il s’agit d’un tournoi (avec des implications ICM ultérieures), la réponse n’est pas si simple.

Pour déterminer si nous devons appeler ou plier à cet endroit dans un tournoi, nous devons déterminer le tournoi EV de chaque option! Pour ce faire, il faut prendre la probabilité de chaque résultat (victoire, égalité, défaite), les multiplier par la puce EV que chaque résultat apporterait (en fonction des nouvelles piles de jetons après la main).

Et ensuite les additionner pour arriver au total du nouveau tournoi EV pour faire un appel:

% de Chances de Victoire/ Défaite / Égalité Tournoi EV (% de la cagnotte) après la main

Victoire: 47,69% x 38,72%

Égalité: 3,10% x 25,45% (coupant les SB/antes des autres joueurs)

Perdre: 49,21% x 0%

p>

En additionnant tous ces résultats ensemble, nous pouvons voir que notre tournoi EV, basé sur ICM, si nous l’appelions ici serait 18.47% + 0.79% + 0% = ~19.25%.

Maintenant, nous devons comparer cela à notre équité de tournoi si nous avons plié. Après la main, les nouvelles tailles de pile seraient les suivantes (en raison de la perte de blinds / antes):

• BB (Héros): 4075
• SB: 4,275
• BTN (Méchant):, 5175,
• CO: 4,475

En branchant ces tailles de pile dans une calculatrice ICM, nous pouvons voir que notre nouvelle équité de tournoi (à la suite du pliage ) serait de 23,47%. En appelant QJs ici, nous perdrons une étonnante (23.47% – 19.25%) = 4.22% de notre équité de tournoi (en moyenne) en appelant ici, ce qui est assez considérable!

En conséquence, nous pouvons voir comment dans un cash game basé sur les cotes du pot et la même situation, ce serait un appel facile. Cependant, avec des implications ICM dans un SNG à 9 hommes sur la bulle, ce QJs devient soudainement un « jet dans la boue » facile. »

REMARQUE: Remarquez comment un appel légèrement mauvais (comme illustré ici dans cet exemple SNG) peut entraîner une perte de 4,22% de l’équité du tournoi? Imaginez maintenant une situation similaire avec quatre joueurs à la table finale du Main Event des WSOP ! Avec environ 23 millions de dollars à gagner dans les quatre dernières places (selon la structure de paiement de 2019), 4.l’équité de 22% équivaut à une perte énorme de 970 600 equity en équité monétaire!

Logiciel de GIC pour la pratique de la GIC: Le jeu Push / Fold

La structure de paiement d’un tournoi (en plus de relier la taille actuelle de la pile à celle de tous les autres) aide certainement à déterminer quelle sera la façon la plus rentable de jouer.

Alors que les exemples ci-dessus montrent la pointe de l’iceberg pour les calculs manuels, la bonne nouvelle est que les logiciels peuvent aider. Plusieurs programmes ont été développés pour aider les joueurs à améliorer leur jeu push / fold et leur gameplay global pour les spots ICM comme ceux ci-dessus.

Des applications mobiles comme SnapShove peuvent vous donner un point de départ pour améliorer votre jeu all-in-or-fold. Avec des fonctionnalités personnalisables telles que le nombre de joueurs, la position de la table, les piles efficaces, les antes et les blinds, cela vous aidera sans aucun doute à lancer le bal dans la bonne direction.

Pour aller plus loin dans votre jeu, et aussi pour intégrer de tels calculs push / fold spécifiquement avec des considérations ICM et de paiement, ICMizer (https://www.icmpoker.com/icmizer/) est un outil cool à examiner qui vous aidera à le faire. (Disponible via le navigateur Web de l’ordinateur et pour téléchargement Windows.) Cela aidera également à simplifier des calculs plus compliqués qui prendraient beaucoup de temps si vous deviez les faire à la main à chaque fois.

En regardant notre dernier exemple, nous aurions facilement pu utiliser ICMizer pour nous montrer les résultats en un instant!

Résumé de l’ICM

Espérons que ce guide complet vous a montré avec succès comment apprendre le poker ICM et comment l’étudier aussi. Bien que l’utilisation de l’ICM ne soit certainement pas une solution parfaite (c’est-à-dire qu’elle ne prend pas de compétences, de positions de joueurs, de qui publie sa prochaine grosse blind, etc. ), cela permet aux joueurs d’avoir une compréhension de base de leur équité de tournoi actuelle.

En étudiant avec le logiciel recommandé ci-dessus (et peut-être en essayant quelques exemples ICM de votre choix), connaître le Modèle de puce indépendant améliorera finalement votre gameplay.

Il vous permettra également de prendre plus de décisions + EV, et vous aidera ensuite à gagner plus d’argent aux feutres dans les tournois de poker.