Introduction à l’Estimation de Mouvement avec Flux Optique

Dans ce tutoriel, nous plongeons dans les fondamentaux du Flux Optique, examinons certaines de ses applications et implémentons ses deux principales variantes (clairsemée et dense). Nous discutons également brièvement des approches plus récentes utilisant l’apprentissage en profondeur et des orientations futures prometteuses.

Des percées récentes dans la recherche en vision par ordinateur ont permis aux machines de percevoir son monde environnant grâce à des techniques telles que la détection d’objets pour détecter des instances d’objets appartenant à une certaine classe et la segmentation sémantique pour une classification par pixel.

Cependant, pour le traitement de l’entrée vidéo en temps réel, la plupart des implémentations de ces techniques n’adressent que les relations d’objets dans la même trame \((x,y)\) sans tenir compte des informations temporelles \((t)\). En d’autres termes, ils réévaluent chaque image indépendamment, comme s’il s’agissait d’images complètement indépendantes, pour chaque exécution. Cependant, que se passe-t-il si nous avons besoin des relations entre les trames consécutives, par exemple, nous voulons suivre le mouvement des véhicules à travers les trames pour estimer sa vitesse actuelle et prédire sa position dans la trame suivante?

Ou, alternativement, que se passe-t-il si nous avons besoin d’informations sur les relations de pose humaine entre des images consécutives pour reconnaître les actions humaines telles que le tir à l’arc, le baseball et le basket-ball?

Dans ce tutoriel, nous allons apprendre ce qu’est le flux optique, comment implémenter ses deux principales variantes (clairsemée et dense), et aussi avoir une vue d’ensemble des approches plus récentes impliquant un apprentissage profond et des orientations futures prometteuses.

Qu’est-ce que le flux optique ?
Mise en œuvre d’un Flux Optique Clairsemé
Mise en œuvre d’un Flux Optique Dense
Apprentissage profond et au-delà

Qu’est-ce que le flux optique?

Commençons par une compréhension de haut niveau du flux optique. Le flux optique est le mouvement d’objets entre des images consécutives de séquence, causé par le mouvement relatif entre l’objet et la caméra. Le problème du flux optique peut s’exprimer par:

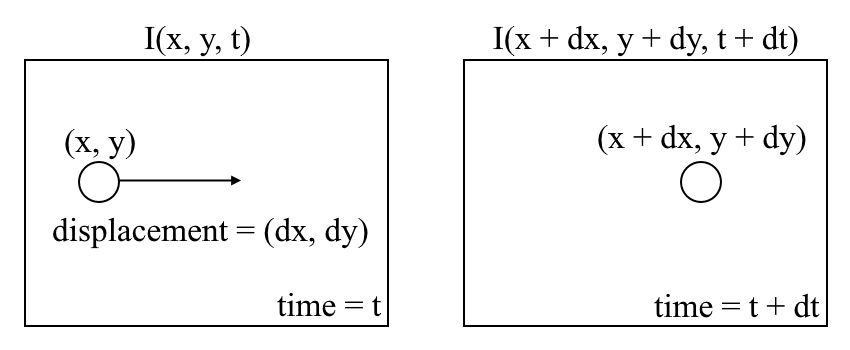
où entre des images consécutives, nous pouvons exprimer l’intensité de l’image \((I)\) en fonction de l’espace \((x,y)\) et le temps \((t)\). En d’autres termes, si nous prenons la première image \(I(x, y, t)\) et déplaçons ses pixels de \((dx, dy)\) sur \(t\) temps, nous obtenons la nouvelle image \(I(x + dx, y + dy, t +dt)\).

Tout d’abord, nous supposons que les intensités de pixels d’un objet sont constantes entre des images consécutives.

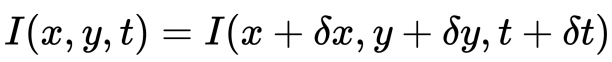
Deuxièmement, nous prenons l’approximation de la série de Taylor du RHS et supprimons les termes communs.

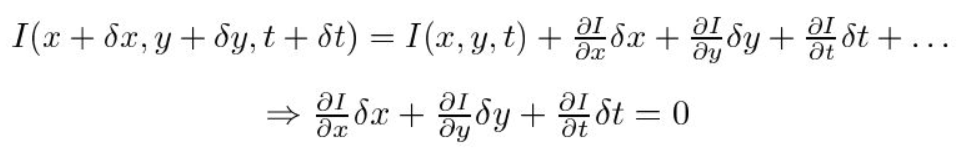
Troisièmement, nous divisons par \(dt\) pour dériver l’équation de flux optique:

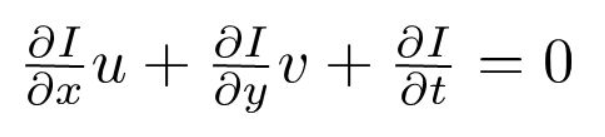
où \(u= dx/dt\) et \(v =dy/dt\).

\(dI/dx, dI/dy\) et \(dI/dt\) sont les gradients d’image le long de l’axe horizontal, de l’axe vertical et du temps. Par conséquent, nous concluons avec le problème du flux optique, c’est-à-dire en résolvant \(u(dx / dt) \) et \(v(dy / dt) \) pour déterminer le mouvement dans le temps. Vous remarquerez peut-être que nous ne pouvons pas résoudre directement l’équation de flux optique pour \(u\) et \(v\) car il n’y a qu’une seule équation pour deux variables inconnues. Nous allons implémenter certaines méthodes telles que la méthode Lucas-Kanade pour résoudre ce problème.

Flux optique clairsemé vs Dense

Flux optique clairsemé donne les vecteurs de flux de certaines « caractéristiques intéressantes » (disons quelques pixels représentant les bords ou les coins d’un objet) dans le cadre tandis que flux optique dense, ce qui donne les vecteurs de flux de l’ensemble du cadre (tous les pixels) – jusqu’à un vecteur de flux par pixel. Comme vous l’auriez deviné, le flux optique dense a une plus grande précision au prix d’être lent / coûteux en calcul.

Implémentation d’un flux optique clairsemé

Le flux optique clairsemé sélectionne un ensemble de pixels d’entités clairsemées (par exemple des entités intéressantes telles que les bords et les coins) pour suivre ses vecteurs de vitesse (mouvement). Les caractéristiques extraites sont transmises dans la fonction de flux optique d’une image à l’autre pour s’assurer que les mêmes points sont suivis. Il existe diverses implémentations de flux optique clairsemé, y compris la méthode Lucas–Kanade, la méthode Horn–Schunck, la méthode Buxton–Buxton, etc. Nous utiliserons la méthode Lucas-Kanade avec OpenCV, une bibliothèque open source d’algorithmes de vision par ordinateur, pour la mise en œuvre.

Configuration de votre environnement

Si vous n’avez pas déjà installé OpenCV, ouvrez Terminal et exécutez :

pip install opencv-python

Maintenant, clonez le référentiel du tutoriel en exécutant :

git clone https://github.com/chuanenlin/optical-flow.git

Ensuite, ouvrez sparse-starter.py avec votre éditeur de texte. Nous allons écrire tout le code dans ce fichier Python.

Configuration d’OpenCV pour lire une vidéo et configuration des paramètres

Détecteur de coin Shi-Tomasi – sélection des pixels à suivre

Pour la mise en œuvre d’un flux optique clairsemé, nous ne suivons que le mouvement d’un ensemble de pixels. Les caractéristiques des images sont des points d’intérêt qui présentent des informations riches sur le contenu de l’image. Par exemple, ces caractéristiques peuvent être des points de l’image qui sont invariants aux changements de translation, d’échelle, de rotation et d’intensité tels que les coins.

Le détecteur de coin Shi-Tomasi est très similaire au détecteur de coin Harris populaire qui peut être mis en œuvre par les trois procédures suivantes:

1. Déterminer les fenêtres (petites taches d’image) avec de grands gradients (variations de l’intensité de l’image) lorsqu’elles sont traduites dans les deux directions \(x\) et \(y\).
2. Pour chaque fenêtre, calculez un score \(R\).
3. Selon la valeur de \(R\), chaque fenêtre est classée comme un plat, un bord ou un coin.

Si vous souhaitez en savoir plus sur une explication mathématique étape par étape du détecteur de coin Harris, n’hésitez pas à parcourir ces diapositives.

Shi et Tomasi ont plus tard apporté une modification petite mais efficace au détecteur de coin Harris dans leur papier Good Features to Track.

La modification concerne l’équation dans laquelle le score \(R\) est calculé. Dans le détecteur de coin Harris, la fonction de notation est donnée par:

^
\begin{array}{c} {R= \nom de l’opérateur {det} M-k(\nom de l’opérateur {trace}M) ^{2}} \ nouvelle ligne \
{\nom de l’opérateur{det} M = \lambda_{1}\lambda_{2}} \ nouvelle ligne\
{\nom de l’opérateur{trace} M =\lambda_{1}+\lambda_{2}} \ fin { tableau }
R

À la place, Shi-Tomasi a proposé la fonction de notation comme suit:

R
R = \min\left(\lambda_{1}, \lambda_{2}\right)
which

ce qui signifie essentiellement que si \(R\) est supérieur à un seuil, il est classé comme un coin. Ce qui suit compare les fonctions de notation de Harris (à gauche) et de Shi-Tomasi (à droite) dans l’espace \(λ1-λ2\).

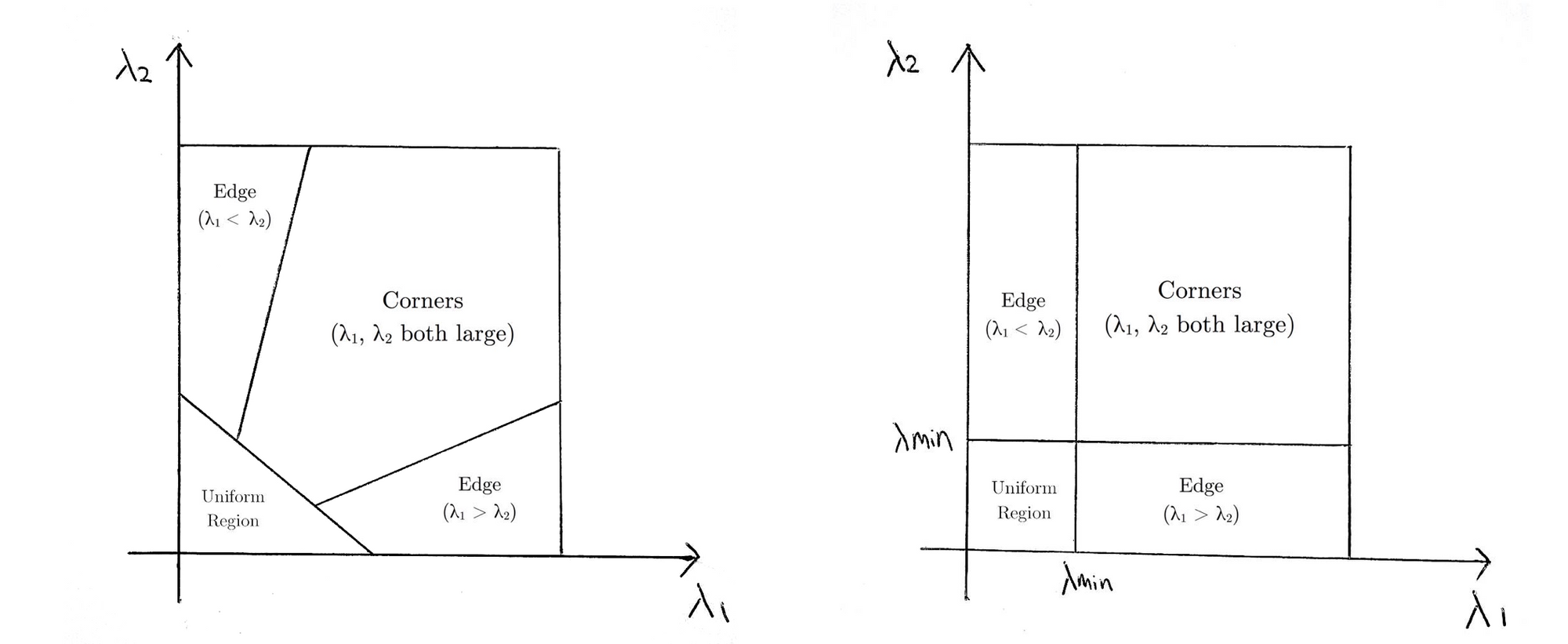
Pour Shi-Tomasi, seulement lorsque \(λ1\) et \(λ2\) sont au-dessus d’un seuil minimum \(λmin\) est la fenêtre classée comme un coin.

La documentation de l’implémentation de Shi-Tomasi par OpenCV via goodFeaturesToTrack() peut être trouvée ici.

Suivi d’objets spécifiques

Il peut y avoir des scénarios où vous souhaitez suivre uniquement un objet spécifique d’intérêt (par exemple, suivre une certaine personne) ou une catégorie d’objets (comme tous les véhicules à 2 roues en circulation). Vous pouvez facilement modifier le code pour suivre les pixels du ou des objets que vous souhaitez en changeant la variable prev.

Vous pouvez également combiner la détection d’objet avec cette méthode pour estimer uniquement le flux de pixels dans les zones de délimitation détectées. De cette façon, vous pouvez suivre tous les objets d’un type / catégorie particulier dans la vidéo.

Lucas-Kanade: Flux Optique Clairsemé

Lucas et Kanade ont proposé une technique efficace pour estimer le mouvement de caractéristiques intéressantes en comparant deux images consécutives dans leur article Une Technique d’Enregistrement d’Image Itérative avec une Application à la Vision Stéréo. La méthode Lucas-Kanade fonctionne sous les hypothèses suivantes:

1. Deux trames consécutives sont séparées par un petit incrément de temps (\(dt\)) de sorte que les objets ne soient pas déplacés de manière significative (en d’autres termes, la méthode fonctionne mieux avec des objets lents).
2. Un cadre représente une scène « naturelle » avec des objets texturés présentant des nuances de gris qui changent en douceur.

Tout d’abord, sous ces hypothèses, nous pouvons prendre une petite fenêtre 3×3 (voisinage) autour des caractéristiques détectées par Shi-Tomasi et supposer que les neuf points ont le même mouvement.

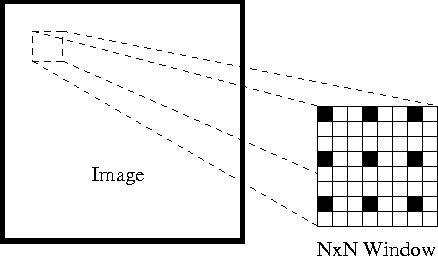
Ceci peut être représenté par

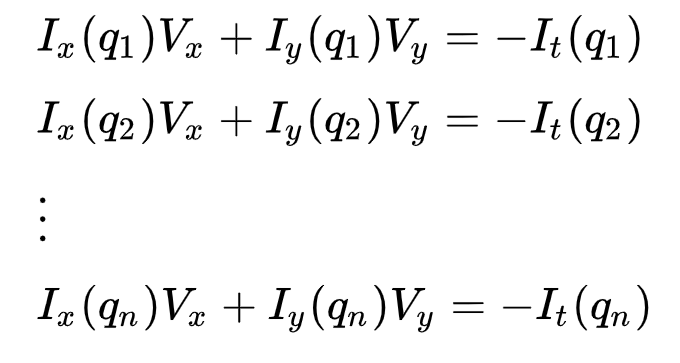
où \(q_1, q_2, …, q_n\) désignent les pixels à l’intérieur de la fenêtre (par exemple \(n\) = 9 pour une fenêtre 3×3) et \(I_x(q_i)\), \(I_y(q_i)\) et \(I_t(q_i)\) désignent les dérivées partielles de l’image \(I\) par rapport à la position \((x, y )\) et time\(t\), pour le pixel\(q_i\) à l’heure actuelle.

Ce n’est que l’Équation de flux optique (que nous avons décrite précédemment) pour chacun des n pixels.

L’ensemble des équations peut être représenté sous la forme matricielle suivante où \(Av=b\) :

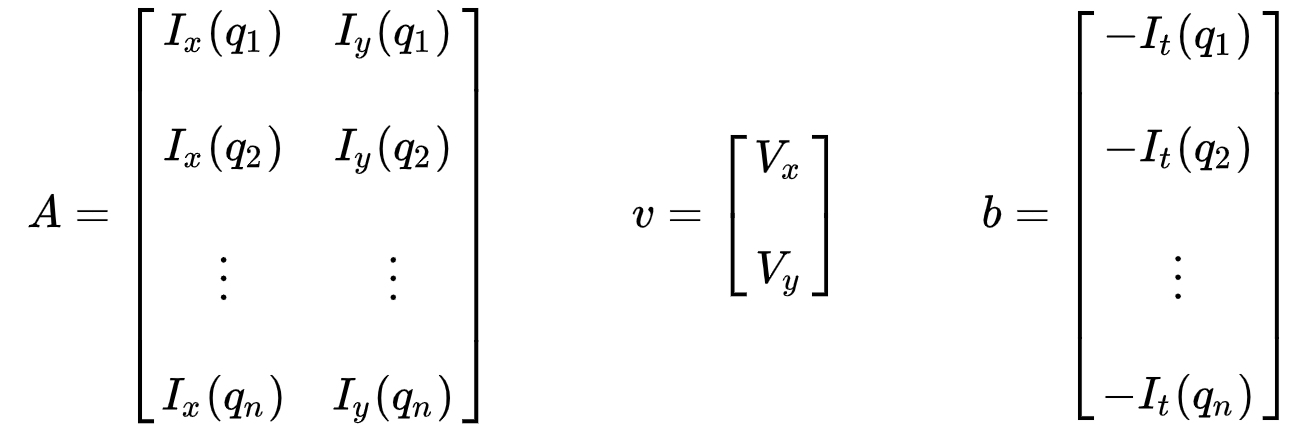
Prenez note cela précédemment (voir « Qu’est-ce que le flux optique? »section), nous avons fait face au problème de devoir résoudre pour deux variables inconnues avec une équation. Nous devons maintenant résoudre deux inconnues (\(V_x\) et \(V_y\)) avec neuf équations, ce qui est sur-déterminé.

Deuxièmement, pour résoudre le problème sur-déterminé, nous appliquons l’ajustement des moindres carrés pour obtenir le problème suivant à deux équations deux inconnues:

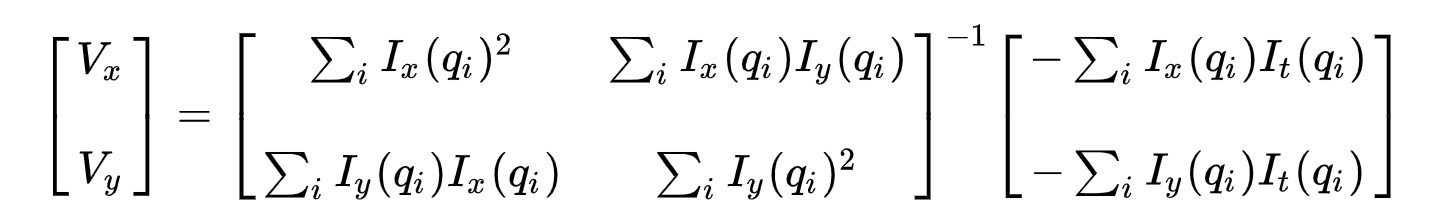
où \(Vx=u=dx/dt\) désigne le mouvement de \(x\) dans le temps et \(Vy=v=dy/dt\) désigne le mouvement de y dans le temps. La résolution des deux variables complète le problème du flux optique.

En un mot, nous identifions quelques fonctionnalités intéressantes pour suivre et calculer de manière itérative les vecteurs de flux optiques de ces points. Cependant, l’adoption de la méthode de Lucas-Kanade ne fonctionne que pour les petits mouvements (de notre hypothèse initiale) et échoue lorsqu’il y a un grand mouvement. Par conséquent, l’implémentation OpenCV de la méthode Lucas-Kanade adopte des pyramides.

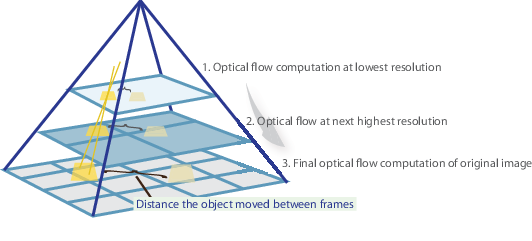
Dans une vue de haut niveau, les petits mouvements sont négligés lorsque nous montons la pyramide et les grands mouvements sont réduits à de petits mouvements – nous calculons le flux optique avec l’échelle. Une explication mathématique complète de l’implémentation d’OpenCV peut être trouvée dans les notes de Bouguet et la documentation de l’implémentation d’OpenCV de la méthode Lucas-Kanade via calcOpticalFlowPyrLK() peut être trouvée ici.

Visualiser

Et c’est tout ! Ouvrez Terminal et exécutez

python sparse-starter.py

pour tester votre implémentation de flux optique clairsemé. In

Si vous avez manqué un code, le code complet se trouve dans sparse-solution.py .

Implémentation d’un flux optique dense

Nous avons précédemment calculé le flux optique pour un ensemble de pixels clairsemé. Le flux optique dense tente de calculer le vecteur de flux optique pour chaque pixel de chaque image. Bien qu’un tel calcul puisse être plus lent, il donne un résultat plus précis et un résultat plus dense adapté à des applications telles que la structure d’apprentissage à partir de segmentation de mouvement et de vidéo. Il existe différentes implémentations de flux optique dense. Nous utiliserons la méthode Farneback, l’une des implémentations les plus populaires, en utilisant OpenCV, une bibliothèque open source d’algorithmes de vision par ordinateur, pour la mise en œuvre.

Configuration de votre environnement

Si vous ne l’avez pas déjà fait, veuillez suivre l’étape 1 de la mise en œuvre du flux optique clairsemé pour configurer votre environnement.

Ensuite, ouvrez dense-starter.py avec votre éditeur de texte. Nous allons écrire tout le code dans ce fichier Python.

Configurer OpenCV pour lire une vidéo

Flux optique de Farneback

Gunnar Farneback a proposé une technique efficace pour estimer le mouvement de caractéristiques intéressantes en comparant deux images consécutives dans son article Estimation du Mouvement à Deux images Basée sur l’expansion polynomiale.

Tout d’abord, la méthode rapproche les fenêtres (voir la section Lucas Kanade de l’implémentation de flux optique clairsemé pour plus de détails) de trames d’images par polynômes quadratiques grâce à une transformée d’expansion polynomiale. Deuxièmement, en observant comment le polynôme se transforme en translation (mouvement), une méthode pour estimer les champs de déplacement à partir des coefficients d’expansion polynomiaux est définie. Après une série de raffinements, un flux optique dense est calculé. L’article de Farneback est assez concis et simple à suivre, je vous recommande donc fortement de le parcourir si vous souhaitez mieux comprendre sa dérivation mathématique.

Pour l’implémentation d’OpenCV, il calcule l’amplitude et la direction du flux optique à partir d’un tableau de vecteurs de flux à 2 canaux \((dx/dt, dy/dt)\), le problème du flux optique. Il visualise ensuite l’angle (direction) de l’écoulement par teinte et la distance (amplitude) de l’écoulement par valeur de la représentation des couleurs HSV. La force du HSV est toujours réglée à un maximum de 255 pour une visibilité optimale. La documentation de l’implémentation par OpenCV de la méthode Farneback via calcOpticalFlowFarneback() peut être trouvée ici.

Visualiser

Et c’est tout ! Ouvrez Terminal et exécutez

python dense-starter.py

pour tester votre implémentation de flux optique dense. In

Si vous avez manqué un code, le code complet peut être trouvé dans dense-solution.py .

Flux optique utilisant le Deep Learning

Alors que le problème du flux optique a toujours été un problème d’optimisation, les approches récentes par application du deep learning ont montré des résultats impressionnants. Généralement, de telles approches prennent deux trames vidéo en entrée pour sortir le flux optique (image codée par couleur), qui peut être exprimé comme suit:

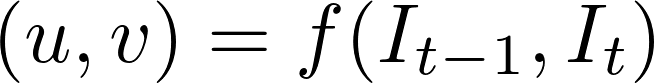
où \(u\) est le mouvement dans la direction \(x\), \(v\) est le mouvement dans la direction \(y\) et \(f\) est un réseau de neurones qui prend deux trames consécutives \(I_{t-1}\) (frame at time = \(t-1)\) et \(I_t\) (frame at time = \(t)\) comme entrée.

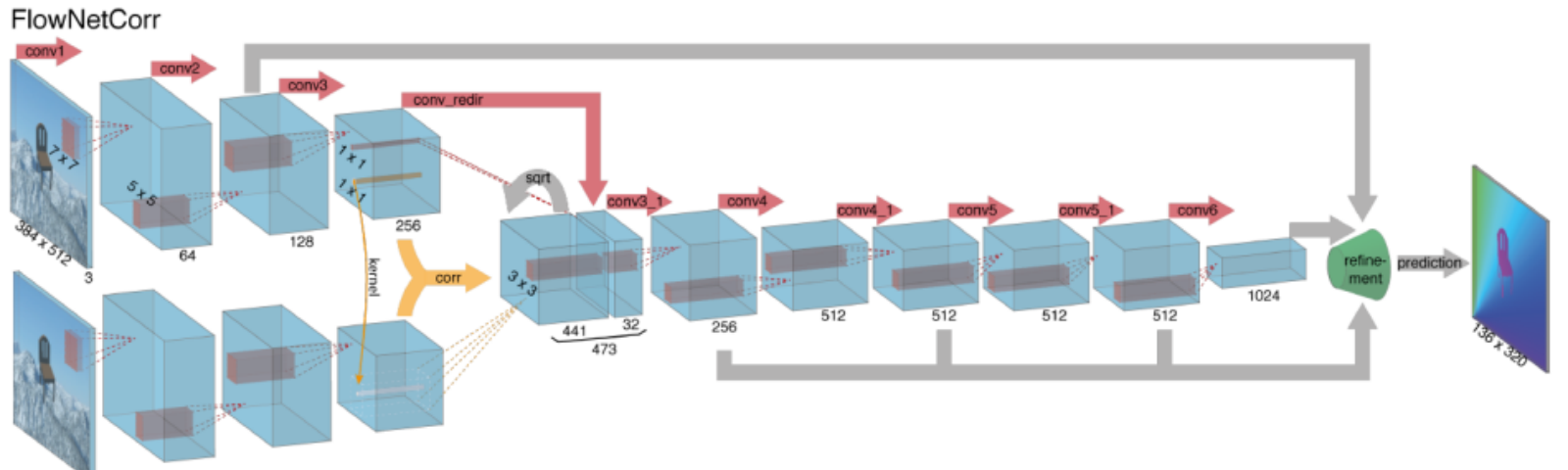
Le calcul du flux optique avec des réseaux de neurones profonds nécessite de grandes quantités de données d’entraînement, ce qui est particulièrement difficile à obtenir. En effet, l’étiquetage des séquences vidéo pour le flux optique nécessite de déterminer avec précision le mouvement exact de chaque point d’une image à une précision inférieure aux pixels. Pour résoudre le problème de l’étiquetage des données de formation, les chercheurs ont utilisé l’infographie pour simuler des mondes réalistes massifs. Puisque les mondes sont générés par des instructions, le mouvement de chaque point d’une image dans une séquence vidéo est connu. Parmi ces exemples, citons MPI-Sintel, un film CGI open-source avec un étiquetage de flux optique rendu pour diverses séquences, et Flying Chairs, un ensemble de données de nombreuses chaises volant sur des arrière-plans aléatoires également avec un étiquetage de flux optique.

Résoudre des problèmes de flux optique avec l’apprentissage en profondeur est un sujet extrêmement brûlant en ce moment, avec des variantes de FlowNet, SPyNet, PWC-Net, etc., qui se surpassent les unes les autres sur divers benchmarks.

Application du flux optique : Segmentation sémantique

Le champ de flux optique est une vaste mine d’informations pour la scène observée. À mesure que les techniques de détermination précise du flux optique s’améliorent, il est intéressant de voir des applications du flux optique en jonction avec plusieurs autres tâches fondamentales de visions informatiques. Par exemple, la tâche de la segmentation sémantique consiste à diviser une image en séries de régions correspondant à des classes d’objets uniques, mais les objets étroitement placés avec des textures identiques sont souvent difficiles pour les techniques de segmentation à une seule image. Cependant, si les objets sont placés séparément, les mouvements distincts des objets peuvent être très utiles lorsque la discontinuité dans le champ d’écoulement optique dense correspond à des limites entre les objets.

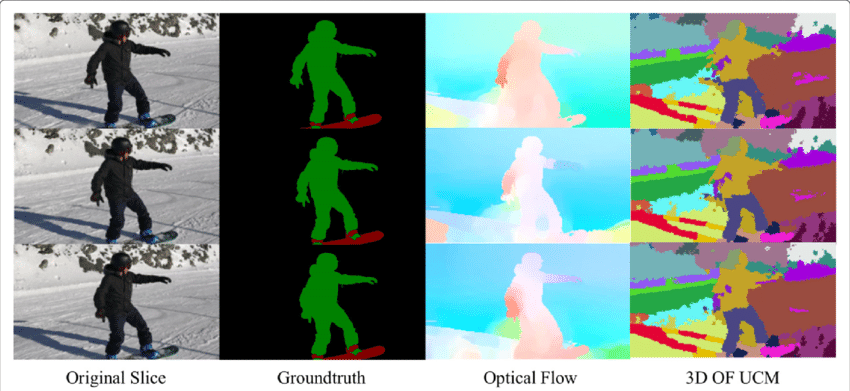
Application du flux optique: Détection d’objets & Suivi

Une autre application prometteuse du flux optique peut être la détection et le suivi d’objets ou, sous une forme de haut niveau, vers la construction de systèmes de suivi des véhicules et d’analyse du trafic en temps réel. Étant donné que le flux optique clairsemé utilise le suivi de points d’intérêt, de tels systèmes en temps réel peuvent être réalisés par des techniques de flux optique basées sur des caractéristiques à partir d’une caméra fixe ou de caméras fixées à des véhicules.

Conclusion

Fondamentalement, les vecteurs de flux optiques servent d’entrée à une myriade de tâches de niveau supérieur nécessitant une compréhension de la scène des séquences vidéo, alors que ces tâches peuvent servir de blocs de construction à des systèmes encore plus complexes tels que l’analyse des expressions faciales, la navigation autonome dans les véhicules, et bien plus encore. Les nouvelles applications du flux optique encore à découvrir ne sont limitées que par l’ingéniosité de ses concepteurs.

Paresseux pour coder, vous ne voulez pas dépenser en GPU? Rendez-vous sur Nanonets et construisez des modèles de vision par ordinateur gratuitement!