不対電子の検出には実験的な方法があります。 材料中の不対電子の特徴の一つは、磁場との相互作用である。 その相互作用は、不対電子を含む化合物に関する情報を提供するために使用することができる。電子常磁性共鳴(EPR)または電子スピン共鳴(ESR)は分光法である。
電子常磁性共鳴(EPR)または電子スピン共鳴(ESR)は分光法である。
電子常磁性共鳴(EPR) これは、磁場の存在下でのみ存在する二つのスピン状態のエネルギー分離に依存する。EPRは、他の一般的なタイプのスピン共鳴分光法、NMRと非常に密接に関連しています。
EPRは非常に密接に関連しています。スピンは、巨視的なレベルで私たちに意味をなさない本当の類推を持たない量子特性です。
スピンは、物理的な性質ではありません。
スピンは、 しかし、私たちはスピンがそれに磁気特性を関連させていることを知っています。 電子は、これらの磁気特性のための二つの値のいずれかを持つことができます。 これらの値にはさまざまなラベルが与えられています:時には”上”と”下”、時には+1/2と-1/2。 しかし、電子が持っているスピンの値はエネルギー的に違いはありません。
磁場が存在しない限り、二つの可能なスピン状態はエネルギー的に同じです。 そのような状況が発生すると、2つの状態の間に活発な分離があります。
磁場の存在下では、二つのスピン状態は二つの異なるエネルギーレベルに分離します。 エネルギー準位間の分離の量は、磁場の大きさに依存する。 磁場が強ければ強いほど、分離は大きくなります。
このケースは、ペアリングされていないスピンに対してのみ当てはまります。 ペアのないスピンは磁場と相互作用することを覚えておいてください。 すべてがスピンペアになっている場合、何も起こりません。 それは私たちにそれらの不対電子を検出する方法を与えるので、それは非常に便利です。
一方のスピン状態の電子は、光子の吸光度によって他方に励起することができます。
一方のスピン状態の電子は、光子の吸光度によっ あるいは、より高い状態の電子は、光子を放出すると、より低い状態の電子にドロップダウンすることができます。
これが起こるためには、光子のエネルギーは状態間のエネルギー差と正確に一致しなければなりません。 このゴルディロックスの法則は共鳴条件と呼ばれています。 あるエネルギーレベルから次のエネルギーレベルにジャンプするために供給されるエネルギーの量は、ちょうど右でなければなりません。 あまりにも少ないエネルギーと電子はそれを作ることはありません。 あまりにも多くのエネルギーと電子はそれを作ることはありません。 それはちょうど右の光子を待っています。
光子はどれくらいのエネルギーを持っていますか? あなたのプランク-アインシュタインの関係を覚えています。 それは光子のエネルギーを記述しました:
\(E=h\nu\)
Eは光子のエネルギー、hはプランク定数(6.625×10-34Js)、λは光子の周波数です(ローマのveeのように見えますが、ギリシャ語の文字、nuです)。
あるいは、波長と周波数の関係のために:新しい量は、c、光の速度(3.0x108m s-1)、λ、光子の波長です。p>
これらの光子の周波数は約9または10GHzです。 (別のタイプの分光学、回転分光学はまた、マイクロ波の吸光度を測定する。 それは普通マイクロ波の幾分より高い頻度を使用する。 回転分光法は、気相中の分子に関する構造的または結合的な情報を与える。)
不対電子の環境によっては、外部磁場の影響を受けやすくなったり、影響を受けにくくなったりすることがあります。 つまり、2つのスピン状態の間のエネルギー分裂は、ある分子から別の分子に変化することを意味します。 その結果、同じ磁場中の異なる分子は、異なる波長のマイクロ波放射を吸収するであろう。
通常、EPR分光計は、サンプルに固定波長のマイクロ波放射を供給するように設計されています。 磁場が調整され、光子の吸収に必要な磁場強度が測定されます。 EPRスペクトルは磁場強度の関数として吸光度を示す。
EPRスペクトルが通常どのように表示されるかについて少し異なるものがあります。 これは、上に示したプロットの導関数として表示されます。 これは、磁場を変化させるときの吸光度の変化を測定する方法のためです。d(吸光度)/d(磁場)を測定します。 それは前のプロットの傾きです。
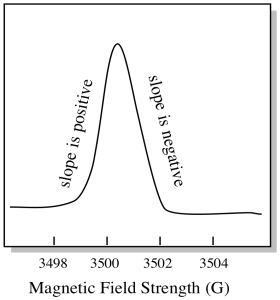
その結果、EPRスペクトルは実際にはこのように見えます。 ベースラインの上の部分は、前のプロットの正の傾きを反映しています。 ベースラインの下の部分は、前のプロットの負の傾きを反映しています。
磁場強度は、通常、ピーク位置について報告される値ではありません。 代わりに、g値と呼ばれるものが報告されます。 G値はZeeman効果(スピンエネルギー準位間の分裂に対する磁場の効果)の方程式から生じる。 その関係は次のとおりです。
\(\Delta e=g\beta B\)
ここで、Δ Eはスピン状態間のエネルギー差、gはg値、電子が磁場の影響を受けやすいかどうかに依存する比例定数、βはボーアマグネトン(9.274×10-24J T-1)、Bは印加磁場である。つまり、光子吸収のために、
\(h\nu=g\beta B\)
つまり、
\(g=\frac{h\nu}{\beta B}\)
覚えておいてください。hとβは単なる定数です。 つまり、gは、使用される磁場に対する吸収された光子の比の尺度であることを意味します。 それは標準化のステップです。 人々がマイクロ波放射のわずかに異なる波長を使用する機器を持っているならば、彼らが同じサンプルのために測定する磁場は一致しないでしょう。 誰もが波長と電界強度の比を測定するだけであれば、それはすべて均等になるはずです。 G値は、ある実験室から別の実験室に同じでなければならない電子の環境の再現可能な尺度です。
同様の理由から、NMR分光法でも同様の方法が使用されています。 Hzではなくppmで化学シフトを報告すると、使用している機器の磁場の強さを補正しています。 それ以外の場合は、同じサンプルは、二つの異なる楽器に二つの異なるシフトを与えるだろう。
EPRにおける結合
結合は、磁場が互いに相互作用する現象である。 EPRでは、観測されている電子に対する近くの核の影響のために結合が起こります。たとえば、水素原子の核には対になっていないスピンがあることをすでに知っているかもしれません。
たとえば、水素原子の核には対になってい それが1H NMR分光法の基礎です。 その核が対になっていないスピンを持っている場合、それは関連する磁場を持っています。 水素核はスピン値+1/2または-1/2のいずれかを持つ可能性があるため、それに関連する2つの可能な磁場があります。
外部磁場に置かれた近くの電子は、現在、二つの異なる状況のいずれかにある可能性があります。 隣接する陽子が磁場に少し加算するか、外部磁場から少し減算するかのいずれかです。p>
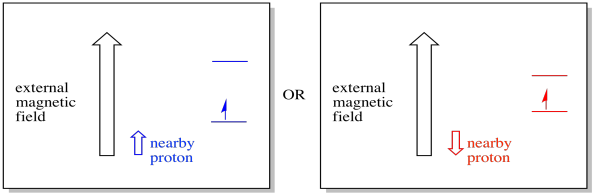
その結果、電子は二つの異なるフィールドを経験することができます。 覚えておいてください、私たちは分光学で単一の分子を扱っていません。 私たちは膨大な数の分子を扱っています。 分子のいくつかは、一つの状況になります。 分子のいくつかは他の状況にあります。 両方の状況が表示されます。 2つの異なる磁場強度で吸光度があります。
スペクトル中のこのタイプのピークは、二重吸光度のために二重項と呼ばれています。 EPRピークのこの特性は、その多重度と呼ばれます。 ピークは何行に分割されていますか? 二つ それは二重です。
近くに二つの陽子があれば、物事はさらに興味深いものです。 その場合、両方の隣接する陽子はスピンを持っています。 どちらのスピンも+1/2または-1/2の値を持つことができます。 多分彼らは両方とも+1/2です。 たぶん、彼らは両方とも-1/2です。 たぶん、それぞれの一つがあります。 これらの3つの可能な組み合わせは、電子が経験する磁場に3つの異なる効果をもたらすでしょう。
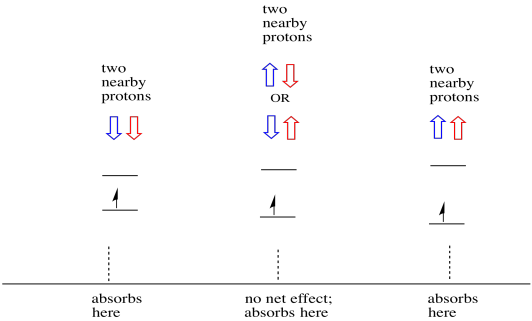
その結果、スペクトルには三つのピークがあります。 スペクトルは三重項と呼ばれます。 この三重項は、隣接する水素のスピンの組み合わせを示す図の下に示されています。
水素のいずれかが混合された組み合わせで上下になる可能性があるため、その中間状態に到達するには二つの方法があ これらの組み合わせを得る方法は1つしかないので、その組み合わせは他の2つの組み合わせの2倍の可能性があります:両方の水素のスピンは、1つのケースでは上昇しています。 両方の水素は、他にダウンしています。 その結果、三重項の中間ピークは、エッジのピークの2倍の大きさになります。3つの隣接する水素では、ピークの比率が1:3:3:1であるカルテットが生じることを示しています。
運動\(\PageIndex{1}\)
ピークの比率が1:3:3:1である。
答え
組み合わせは次のとおりです。
答え:
a)すべてのスピンがダウンしています(そして、それを行うには一つの方法があります)
b)二つのスピンがダウンしていますが、一つはアップしています(そして、三つの陽子のそれぞれがアップすることができますので、三つの方法があります)
c)二つのスピンがアップしていますが、一つはダウンしています(そして、三つの陽子のそれぞれがダウンすることができますので、三つの方法があります)
d)すべてのスピンがアップしています(そして、一つの方法があります)
d)すべてのスピンがアップしています(そして、一つの方法があります)
d)すべてのスピンがアップしています(そして、一つの方法があります)
d)すべてのスピンがアップしています(そして、一つの方法があります)
それ)。結果は1:3:3:1の四重奏です。
結果は1:3:3:1の四重奏です。P>A)x3C-O.b)X2CH-O.c)XCH2-O.d)CH3-O.
回答A)
a)一重項
回答a)x3c-o.b)X2CH-o.c)XCH2-o.d)CH3-O.回答a)x3c-o.b)X2CH-o.c)XCH2-o.d)CH3-O.回答a)x3c-O.b)x2CH-o.c)XCH2-o.d)CH3-O.回答a)x3c-O.b)x2CH-o.c)XCH2-o.d)CH3-O.回答a)x3c-O.c)x2CH-o.c)xch2-o.c)xch3-o.c)xch3-o.c)xch3-o.c)xch3-o.b)
b)二重項
回答C)
c)三重項
回答d)
d)四重項
練習\(\pageindex{3}\)
ベンゼンラジカルアニオンを得るためにベンゼンを一つの電子で還元したとします。 EPRスペクトルの多重度は何でしょうか?
答え答え答え答え答え答え1:3:5:7:5:3:1 比)。
金属イオンへの結合
水素以外の多くの核は正味のスピンを持っています。 不対電子が金属上に発見された場合、EPRスペクトルはその構造情報の確認を提供する可能性があります。 この確認は、磁場情報(NMRの化学シフトに似ている)と多重度の両方から来る可能性があります。
選択された金属の核スピンを以下に示す。/td>
これらの金属のそれぞれで、核は異なる可能な磁場を持 それらの効果は水素原子の効果よりもわずかに複雑であることに注意してください。 例えば、スピン3/2を持つ銅は、近くのelectromのEPRスペクトルへの影響の点で、三つの異なる水素核(それぞれスピン+/-1/2を持つ)のように少し作用する。 銅イオン上の不対電子の多重度はかなり特徴的でなければならない。P>
運動\(\PageIndex{4}\)
次の各金属上の不対電子のEPRスペクトルのピークの多重度を予測します。
a)バナジウムb)マンガンc)鉄d)コバルトe)銅
答えa)
a)オクテット(a)(a)(b)(b)(c)(c)(c)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d)(d1:3:5:7:7:5:3:1 1:3:5:5:3
:1比)回答c)
c)一重項
回答d)
d)オクテット
回答e)
e)カルテット(1:3:3:1比)
同じ元素の異なる同位体が異なる可能性のあるスピン値を 実際には、それは水素と炭素にも当てはまりますが、水素の大部分は1Hであるため、一般的にはスピン=1/2を持つと考えることができます。
鉄の天然同位体とその核スピンを下の表に示します。
| Isotope | Spin | % Abundance |
| 54Fe | 0 | 5.9 |
| 56Fe | 0 | 91.8 |
| 57Fe | 1/2 | 2.1 |
| 58Fe | 0 | 0.2 |
The EPR spectrum of an unpaired electron on iron may be slightly more complicated than we first thought. サンプル内では、電子の一部はスピン=1/2の鉄イオン上に位置しますが、ほとんどはそうではありません。 この複雑さは、スペクトルの外観にわずかな変化を導入するのに十分かもしれませんが、全体的にはまだ一重項のように見えます。しかし、多くの場合、物事ははるかに複雑になります。
しかし、多くの場合、物事ははるかに複雑になります。 モリブデンは良い例を提供します。
98mo
モリブデンの天然に存在する同位体があります。 それらのうちの5つはspin=0であるため、これらの同位体上の不対電子はEPRスペクトルの単純な一重項を生じさせるでしょう。 他の2つの同位体は全体の25%を占め、スピン=5/2である。 モリブデン上のほとんどの不対電子は一重項として現れるであろう。 しかし、かなりの部分はsextetとして表示されます。 つまり、理想的なケースでは、モリブデン上の不対電子は、それに重畳された六重項(一重項と同じくらい強い約四分の一)を有する一重項を生じるであろう。この状況は、以下の図のようになります。
この状況は、次の図のようになります。
p>
実際には、EPRスペクトルは多くの場合非常に複雑です。 彼らはしばしばあいまいな塊のように見えます。 それは目で解読することはほとんど不可能になるので、他の多くのものに結合するので、多くのものがあります。 ほとんどの場合、計算機シミュレーションを実行し、実験データを計算機シミュレーションと比較して構造的洞察を得ます。バナジウムはいくつかのニトロゲナーゼに存在するので、モデル複合体に関心がありました(例えば、Sandro Gambarotta et al,J.Am. ケム Soc. 1994, 116, 6927-6928). Gambarottaは、THF溶媒中で、以下の合成を使用しました:3V(THF)}\)
- 反応の生成物の構造を描きます。
- この複合体のd軌道分割図を描画します。
- この化合物についてEPRスペクトルを記録した。 バナジウムが核スピンI=7/2を持つことを考えると、スペクトルをスケッチする。
- この化合物のμ effを推定します。
この化合物はN2と反応し、N2-架橋二量体を形成する。
e)この製品の構造を描きます。
f)この化合物はEPRスペクトルを生成しません。 この観測を説明する(e)の共鳴構造を提供する。P>答え
Eprスペクトルは、仮想想像力/Slapdash化学作品の礼儀を提供しました。
属性
Chris P Schaller、Ph.D.(聖ベネディクト大学/聖ヨハネ大学)
属性
Chris P Schaller、Ph.D.、(聖ベネディクト大学/聖ヨハネ大学)