Publié en juin 2008.
La deuxième des deux colonnes sur les mathématiques de l’arpentage (la première est ici). …
Bill Casselman
Université de la Colombie-Britannique, Vancouver, Canada
cass at math.ubc.ca 
John Eggers
Université de Californie à San Diego
jeggers à ucsd.edu 
 E-mail à un ami E-mail à un ami |
 Imprimer cet article Imprimer cet article |
Un planimètre est un instrument de table pour mesurer des zones, généralement les zones de régions irrégulières sur une carte ou une photographie. Ils étaient autrefois courants, mais ont maintenant été largement remplacés par des outils numériques.
L’image suivante donne une idée de la configuration. Le bras du poteau tourne librement autour du poteau, qui est fixé sur la table. Le bras traceur tourne autour du pivot, où il rejoint le bras polaire. Vous tracez une courbe dans le sens des aiguilles d’une montre avec le traceur, et au fur et à mesure, la roue de mesure roule et la distance totale qu’elle roule est accumulée sur le cadran. La roue de support empêche la chose de se renverser. À la fin, vous lisez un nombre du cadran, et après multiplication par un facteur dépendant uniquement de la configuration particulière du planimètre, vous obtenez l’aire à l’intérieur de la courbe.

La figure suivante vous donne une meilleure vue du mécanisme.

Nous appelons le chariot l’ensemble des roues, du cadran et du pivot. Dans l’image suivante, vous pouvez mieux la regarder et voir l’entraînement à vis sans fin qui fait tourner le cadran lorsque la roue de mesure se déplace.

Voici le schéma du planimètre original, tiré de l’article de Jakob Amsler qui l’a introduit:
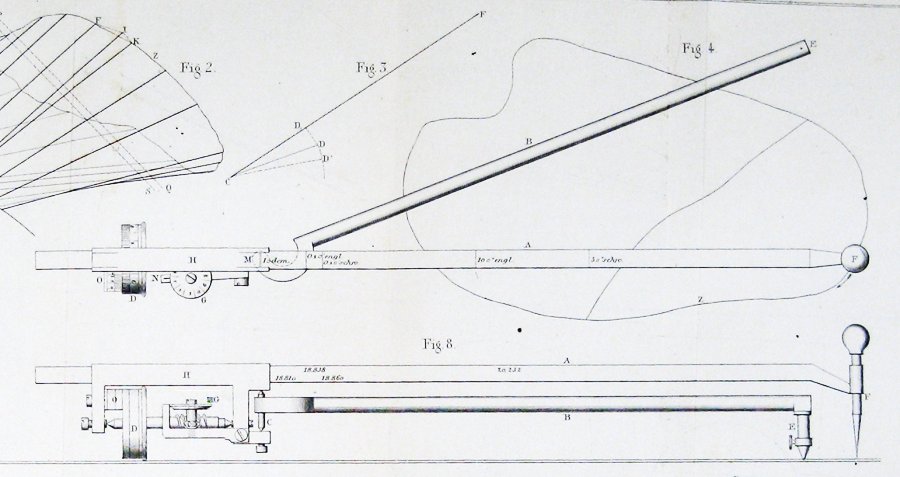
Comment une chose aussi simple peut-elle mesurer des zones?
Géométrie du planimètre
Le mouvement dans le sens horaire du planimètre est le sens opposé à ce que les mathématiciens ont décidé d’être une rotation positive. Plutôt que de violer cette convention, nous allons travailler désormais avec un planimètre de mathématicien, dans lequel vous vous déplacez dans le sens antihoraire. Comme les fantasmes d’autres mathématiciens, il n’y en a pas sur la planète!
Il existe certaines restrictions sur la façon de placer le planimètre par rapport à la courbe que vous souhaitez tracer. Le chariot peut être glissé le long du bras traceur, mais dans tous les cas la longueur l du bras traceur est inférieure à celle de la longueur r du bras polaire. Cela signifie que le traceur ne peut jamais se trouver à une distance r-l du pôle. En revanche, lorsqu’il est complètement étendu, le traceur ne peut jamais dépasser r+l. La courbe à tracer doit donc se situer dans l’anneau entre deux cercles, l’un de rayon r-l, l’autre r+l.

En fait, il devrait devenir clair dans un instant que les bras ne doivent jamais être complètement étendus, de sorte que la courbe à tracer doit se trouver complètement à l’intérieur de l’anneau. De plus, normalement, le poteau est placé à l’extérieur de la courbe.

Pour un point donné de l’anneau, il existe exactement deux configurations possibles du planimètre qui placent le traceur sur ce point. Choisir un point ou l’autre signifie choisir un signe pour une racine carrée. Nous appelons cela le choix d’une orientation pour le planimètre. C’est positif si la racine carrée est positive. Une fois l’orientation choisie, elle restera la même à moins que le bras ne soit complètement étendu. Cela ne doit jamais arriver. Tant que votre courbe est entièrement dans l’anneau, les configurations du planimètre varieront en douceur et de manière unique avec le trajet du traceur.
La prochaine chose à faire est de comprendre quelques choses sur le mouvement de la roue de mesure. Comme le montre l’image suivante, si la roue parcourt en ligne droite une distance C, la roue tourne d’un angle θ = C/R où R est son rayon.

Il est donc vrai que la rotation de la roue et la distance parcourue par le bras traceur ont une certaine relation l’une avec l’autre. Mais cette relation est un peu subtile. Si le bras se déplace tout droit sur une distance C, la zone balayée sera lC, mais s’il se déplace parallèlement à lui-même, la zone balayée sera 0. Dans le premier cas, un point sur la circonférence de la roue se déplacera à la distance C. Dans le second cas, la roue ne bougera pas du tout. Et si le bras se traduit obliquement, la roue tournera sur une distance égale à l’altitude du parallélogramme couvert par le bras. Dans tous les cas où le bras se traduit parallèlement à lui-même, la surface balayée par la portion du bras traceur entre le pivot et le traceur sera égale à lC, où C est la distance mesurée par la rotation de la roue. C’est le fait fondamental qui relie le mouvement du bras au mouvement de la roue de mesure.

La façon de dire ceci avec précision est que quelle que soit la façon dont le bras se déplace, la distance mesurée par la roue est le chemin intégral

où Γ est le chemin parcouru par le point du bras où la roue de mesure est attachée, n est le vecteur unitaire perpendiculaire à la roue de mesure. bras à tout instant, et t est le vecteur unitaire pointant dans le sens de déplacement (de sorte que, par example, si le bras se déplace parallèlement à lui-même, le produit scalaire de n et t est égal à 0).
Théorème de Guldin
Ensuite, nous allons essayer de rendre le comportement du planimètre intuitivement clair, mais nous allons d’abord examiner un type particulier de planimètre, et dans ce cas prouver un résultat plus général. Supposons que nous prenions un seul bras de longueur l en mouvement libre et que nous y attachions une roue de mesure de rayon R en son centre.

Ensuite, nous déplaçons le bras dans l’avion. Si la roue de mesure tourne d’un angle total de θ radians lorsque le bras se déplace, la distance parcourue par un point de la circonférence est C = θR.
Théorème de Guldin. Dans cette situation, la surface totale balayée par le bras est le produit lC.
La zone ici est interprétée avec un signe. Si le bras tourne simplement autour de son centre, une moitié du bras va en avant et l’autre en arrière, et les deux s’annulent.
Nous avons déjà vu que l’assertion de Guldin est valide dans le cas où le bras se traduit simplement. Bien sûr, cela ne se produit pas toujours – le bras peut tourner au fur et à mesure qu’il se déplace et se traduire. Mais nous pouvons voir ce qui se passe en découpant la zone balayée comme suit:

Comme la roue de mesure est au centre du bras, lorsque le bras tourne, elle écrase les petits blocs d’un côté en les dilatant de l’autre. Ces effets s’annulent exactement.
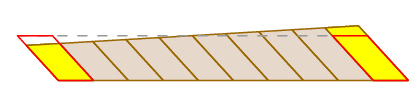
Une preuve complètement rigoureuse peut être donnée en utilisant la formule de changement de variables dans une intégrale double et l’expression de la course de roue comme intégrale de chemin.
Supposons maintenant que la roue soit placée ailleurs. Disons que sa position est c + v où c est le centre du bras et v un vecteur le long du bras. La longueur de v restera fixe, disons à ρ. Le trajet que la roue suit est c(t) + v(t). L’intégrale de chemin est maintenant
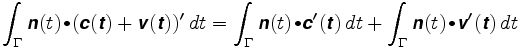
La première intégrale est la distance que parcourrait la roue si elle était au centre du bras. Dans le second, le vecteur v(t) est toujours perpendiculaire à n et v(t) a une longueur constante. Le vecteur v(t) se déplace sur un cercle de rayon égal à ρ. Par conséquent, le produit scalaire de n et v'(t) est juste la longueur signée de v'(t), et la seconde intégrale est égale à ρ fois la rotation totale du bras. Conséquent:
Si la roue est à distance ρ du centre du bras, la distance C que la roue mesure est C0, la distance qui serait mesurée si la roue était au centre, plus ρ fois l’angle total θ que le bras tourne.
Vous pouvez voir immédiatement un cas simple de ceci en tournant le bras autour de son centre. En combinant cela avec le théorème de Guldin, nous voyons que dans tous les cas:
C = C0 + ρ θ
Surface balayée = l C0 = l C -l ρ θ
Le résultat complet
La formule de Guldin donne une zone signée – si vous balayez vers l’arrière sur une zone, la roue recule et vous annulez la zone que vous avez déjà couverte. Si nous appliquons cela au cas où le bras libre revient exactement à l’endroit où il a commencé, nous voyons que lC est égal à l’aire de la région fermée tracée par l’extrémité droite du bras moins celle de la région balayée par la gauche.
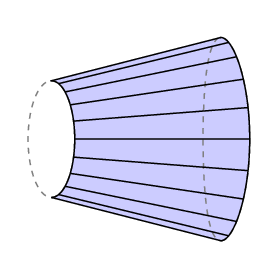
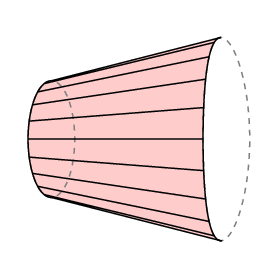

Dans le cas du planimètre polaire, le bas du bras est limité à un arc de cercle de rayon r avec centre au pôle, donc l C est l’aire tracé par le traceur. De plus, normalement le pôle se trouve à l’extérieur de la zone à mesurer, et dans ce cas la rotation totale du bras doit être de 0. Donc, dans ce cas, nous avons
Zone de la région tracée=lC
Voici la figure incluse par Jakob Amsler, l’inventeur, dans son article original sur l’instrument qu’il a inventé:
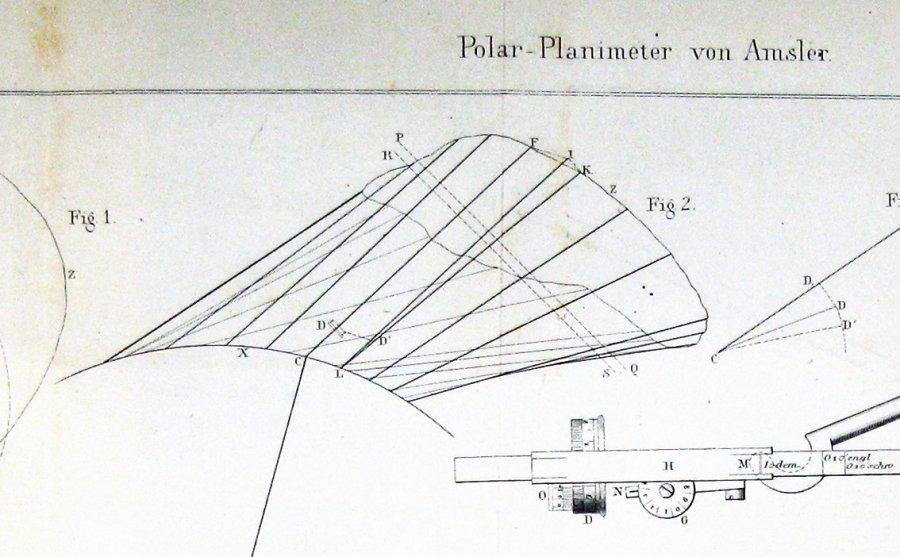
Il semble assez clair d’après cela qu’Amsler a dérivé sa construction par une forme du théorème de Guldin.
Planimètres et Théorème de Green
Comme nous l’avons déjà mentionné, après avoir choisi l’orientation du planimètre, la configuration du planimètre est une fonction continue de la position du traceur. Disons que nous choisissons l’orientation positive. Ensuite, on peut attacher à chaque point de l’anneau un vecteur unitaire n, celui pointant dans le sens antihoraire et perpendiculaire au bras traceur au niveau du traceur.
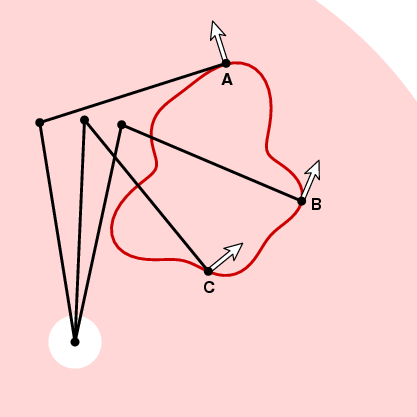
La façon dont la roue de mesure va réagir au mouvement le long de la courbe dans l’instant suivant dépend de l’angle entre ce vecteur et le vecteur tangent unitaire de la courbe. A dans l’image ci-dessus, la roue de mesure ne va pas bouger car le mouvement le long de la courbe est parallèle au bras traceur. À B si le traceur se déplace sur une petite distance ds, la roue de mesure le fera également. Et à C, la roue de mesure se déplacera sur une certaine distance entre 0 et ds. Pour être précis, supposons que t soit le vecteur tangent unitaire en un point de la courbe. Si le traceur déplace la distance ds le long de la courbe, à cet endroit, la roue de mesure se déplace d’une distance d ds, où d = n. t, le produit scalaire des vecteurs unitaires t et n. En d’autres termes, si l’on se déplace tout autour de la courbe Γ la roue de mesure se déplace d’une distance totale égale à l’intégrale de n. t ds (produit scalaire), ou

Mais comme chaque point de l’anneau correspond à une configuration positive unique du planimètre, on peut attribuer un vecteur n à chaque point intérieur de l’anneau, et il définit donc un champ vectoriel. La courbe Γ est la limite de son intérieur Ω, et par l’une de nos hypothèses, elle est entièrement contenue dans la région où n est défini. Le théorème de Green nous dit que l’intégrale de chemin autour de la limite de cette région est également égale à une certaine intégrale sur Ω: Par conséquent,
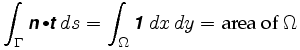
Plus précisément, le théorème de Green nous dit que
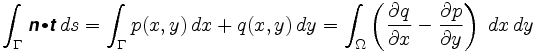
où n= est le champ vectoriel impliqué. L’intégrande dans la double intégrale s’appelle la boucle du champ vectoriel.
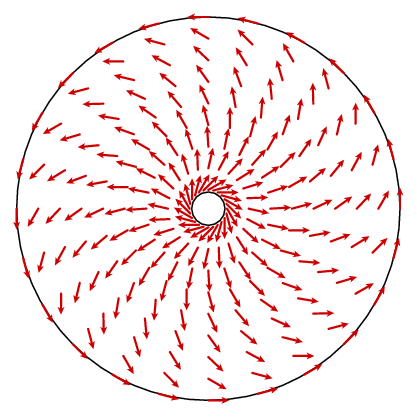
Cela ne semble pas nous amener très loin. Ce qui devrait arriver, c’est que la boucle est une constante 1. En principe, nous pourrions trouver une formule pour le champ vectoriel n et calculer sa boucle, mais ce n’est pas très éclairant. Nous pouvons cependant profiter d’un autre fait. Le champ vectoriel a une symétrie circulaire, ce qui signifie qu’il est déterminé par ce qu’il est sur un rayon. La loi du cosinus nous donne une formule simple pour la composante circonférentielle.
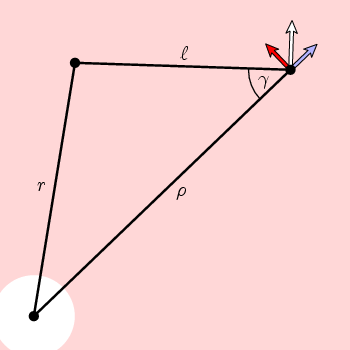
Il résulte de la géométrie simple de cette figure que la composante circonférentielle de n est
f(ρ)= cos(γ)=(ρ 2 + l 2 -r 2)/(2 ρ l)
Le point réel du théorème de Green est que pour vérifier que l’intégrande est 1 il suffit de vérifier que le chemin intégral autour de petits chemins appropriés est le même que la zone. Pour cela, nous choisissons nos régions pour être comme ici:
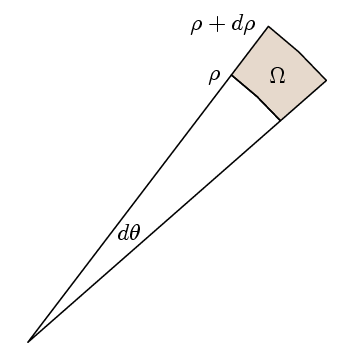
Alors l fois l’intégrale de chemin est
l(ρ + dp)(f(ρ + dp) – f(ρ)) dθ
ou
(θ/2)((ρ+ dp) 2-ρ 2)
qui est l’aire de la région Ω.
Autres types de planimètres
Le théorème de Guldin implique que le mouvement d’une roue de mesure vous indiquera l’aire tracée par le traceur chaque fois que le bras avec une roue de mesure trace une courbe mais a une extrémité limitée à une courbe unidimensionnelle. Cela se produit par example avec le planimètre de roulement, dans lequel le pivot est limité à une ligne droite en étant sur un cylindre de roulement.

En savoir plus
-
 fabrique et vend encore des planimètres.
fabrique et vend encore des planimètres. - Volume II de Calcul différentiel et intégral, R. Courant, Blackie&Son, 1936. La section sur la Formule de Guldin (pp. 294-298) offre une explication du fonctionnement du planimètre.
- Article original d’Amsler, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Il manque les diagrammes, mais ils sont ici:
- Premier diagramme d’Amsler
- Deuxième diagramme d’Amsler
Nos remerciements à Donna Sammis de la bibliothèque universitaire de Stony Brook pour avoir localisé l’article et à son mari Robert pour avoir fourni des photographies des figures.
La société fondée par Amsler a produit des instruments jusqu’au 20ème siècle. Cette photographie montre le logo, sur une version pantographe du planimètre :

- « À propos des planimètres, » Enginersupply. La société a également publié une vidéo sur YouTube.
Bill Casselman
Université de la Colombie-Britannique, Vancouver, Canada
cass at math.ubc.ca 
John Eggers
Université de Californie à San Diego
jeggers à ucsd.edu 
Ceux qui peuvent accéder à JSTOR peuvent y trouver certains des documents mentionnés ci-dessus. Pour ceux qui y ont accès, MathSciNet de l’American Mathematical Society peut être utilisé pour obtenir des informations bibliographiques supplémentaires et des critiques de certains de ces documents. Certains des éléments ci-dessus sont accessibles via le portail ACM, qui fournit également des services bibliographiques.