Magie de l’opérateur Sobel

Enfin, le moment que vous avez tous attendu, le prochain dans notre série d’inférence bayésienne non supervisée: Notre plongée (pas si) profonde dans l’opérateur Sobel.

Un algorithme de détection de bord vraiment magique, il permet l’extraction de caractéristiques de bas niveau et la réduction de la dimensionnalité, réduisant essentiellement le bruit dans l’image. Il a été particulièrement utile dans les applications de reconnaissance faciale.

Enfant d’amour d’Irwin Sobel et Gary Feldman (Laboratoire d’Intelligence Artificielle de Stanford) en 1968, cet algorithme a inspiré de nombreuses techniques modernes de détection de bord. En convoluant deux noyaux ou masques opposés sur une image donnée (par ex. voir ci-dessous à gauche) (chacun capable de détecter des bords horizontaux ou verticaux), nous pouvons créer une représentation moins bruyante et lissée (voir ci-dessous à droite).

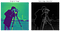
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel valeurs (généralement la luminance) en différenciant la différence entre chaque pixel (le pixel d’ancrage) et ses pixels environnants (se rapprochant essentiellement de la dérivée d’une image).

Cela permet de lisser l’image d’origine et de produire une sortie de dimension inférieure, où les caractéristiques géométriques de bas niveau peuvent être vues plus clairement. Ces sorties peuvent ensuite être utilisées comme entrées dans des algorithmes de classification plus complexes, ou comme exemples utilisés pour le clustering probabiliste non supervisé via la divergence Kullback-Leibler (KLD) (comme vu dans mon récent blog sur LBP).

Générer notre sortie de dimension inférieure nous oblige à prendre la dérivée de l’image. Tout d’abord, nous calculons le dérivé dans les directions x et y. Nous créons deux noyaux 3×3 (voir matrices), avec des zéros le long du centre de l’axe correspondant, deux dans les carrés du centre perpendiculaires au zéro central et un dans chacun des coins. Chacune des valeurs non nulles doit être positive en haut/ à droite des zéros (en fonction de l’axe) et négative de leur côté correspondant. Ces noyaux sont nommés Gx et Gy.

Ceux-ci apparaissent dans le format:

Ces noyaux vont ensuite convoler sur notre image, plaçant le pixel central de chaque noyau sur chaque pixel de l’image. Nous utilisons la multiplication matricielle pour calculer la valeur d’intensité d’un nouveau pixel correspondant dans une image de sortie, pour chaque noyau. Par conséquent, nous nous retrouvons avec deux images de sortie (une pour chaque direction cartésienne).

Le but est de trouver la différence/le changement entre le pixel de l’image et tous les pixels de la matrice de dégradé (noyau) (Gx et Gy). Plus mathématiquement, cela peut être exprimé comme.

Note latérale:

Nous ne convoluons techniquement rien. Bien que nous aimions parler de « circonvolutions » dans les cercles d’IA et d’apprentissage automatique, une convolution impliquerait de retourner l’image originale. Mathématiquement parlant, lorsque nous nous référons à des circonvolutions, nous calculons vraiment la corrélation croisée entre chaque zone 3×3 de l’entrée et le masque pour chaque pixel. L’image de sortie est la covariance globale entre le masque et l’entrée. C’est ainsi que les bords sont détectés.

Retour à notre explication Sobel

Les valeurs calculées pour chaque multiplication matricielle entre le masque et la section 3×3 de l’entrée sont additionnées pour produire la valeur finale du pixel dans l’image de sortie. Cela génère une nouvelle image qui contient des informations sur la présence d’arêtes verticales et horizontales présentes dans l’image d’origine. Il s’agit d’une représentation géométrique de l’image originale. De plus, comme cet opérateur est garanti pour produire la même sortie à chaque fois, cette technique permet une détection de bord stable pour les tâches de segmentation d’image.

À partir de ces sorties, nous pouvons calculer à la fois l’amplitude du gradient et la direction du gradient (en utilisant l’opérateur arctangent) à un pixel donné (x, y):

À partir de cela, nous pouvons déterminer que les pixels de grandes magnitudes sont plus susceptibles d’être un bord dans l’image, tandis que la direction nous informe sur l’orientation du bord (bien que la direction ne soit pas nécessaire pour générer notre sortie).

Une implémentation simple:

Voici une implémentation simple de l’opérateur Sobel en python (en utilisant NumPy) pour vous donner une idée du processus (pour tous les codeurs en herbe).

Cette implémentation est une variante python de l’exemple de pseudocode Wikipedia, visant à montrer comment vous pouvez implémenter cet algorithme, tout en démontrant les différentes étapes du processus.

Pourquoi nous soucions-nous?

Bien que l’approximation du gradient produite par cet opérateur soit relativement grossière, elle fournit une méthode de calcul extrêmement efficace pour calculer les arêtes, les coins et autres caractéristiques géométriques des images. À son tour, il a ouvert la voie à un certain nombre de techniques de réduction de la dimensionnalité et d’extraction de fonctionnalités, telles que les modèles binaires locaux (voir mon autre blog pour plus de détails sur cette technique).

S’appuyer sur des caractéristiques exclusivement géométriques risque de perdre des informations importantes lors de l’encodage de nos données, cependant, le compromis est ce qui permet un prétraitement rapide des données et, à son tour, un entraînement rapide. Par conséquent, cette technique est particulièrement utile dans les scénarios où la texture et les caractéristiques géométriques peuvent être considérées comme très importantes dans la définition de l’entrée. C’est pourquoi la reconnaissance faciale peut être complétée avec un degré de précision relativement élevé à l’aide de l’opérateur Sobel. Cependant, cette technique peut ne pas être le meilleur choix si vous essayez de classer ou de regrouper des entrées qui utilisent la couleur comme principal facteur de différenciation.

Cette méthode est toujours extrêmement efficace pour obtenir une représentation à faible dimension des caractéristiques géométriques et un excellent point de départ pour la dimensionnalité et la réduction du bruit, avant d’utiliser d’autres classificateurs ou pour une utilisation dans les méthodologies d’inférence bayésienne.