13.7 :Franck-Condon-Prinsippet

Franck-Condon-Prinsippet beskriver intensiteten av vibroniske overganger, eller absorpsjon eller utslipp av en foton. Det står at når et molekyl gjennomgår en elektronisk overgang, som ionisering, opplever atomkonfigurasjonen av molekylet ingen signifikant endring. Dette skyldes faktisk at kjerner er mye mer massive enn elektroner, og den elektroniske overgangen foregår raskere enn kjernene kan reagere. Når kjernen tilpasser seg den nye elektroniske konfigurasjonen, sier teorien at den må gjennomgå en vibrasjon.Hvis vi viser den vertikale overgangen fra jord til opphisset elektronisk tilstand som oppstår fra en vibrasjonsbølgefunksjon som gir en sannsynlighetsfordeling for å finne kjernene i et gitt område av rom,kan vi bestemme sannsynligheten for et gitt vibrasjonsnivå fra overlappingsintegralet \(S_{v’, v}\) som gir overlappingen av vibrasjonsbølgefunksjonen i bakken og opphisset tilstand. \(V’\) kvante tallene refererer til grunntilstanden og \(v\) kvante tallene refererer til den opphissede tilstanden. Overgangssannsynligheten kan deles inn i elektroniske og nukleare deler ved Hjelp Av Condon-tilnærmingen.

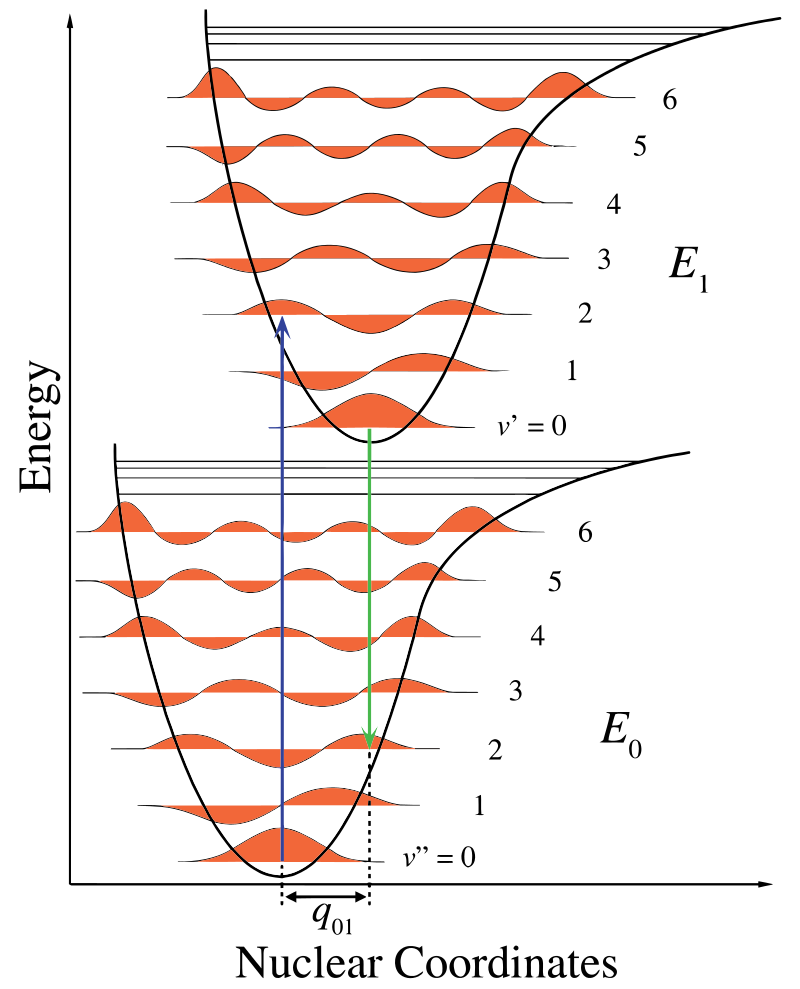
I Figur \(\PageIndex{1}\) viser kjerneaksen en konsekvens av internukleær separasjon og vibronisk overgang er indikert med de blå og grønne vertikale pilene. Denne figuren viser tre ting:

1. en absorpsjon fører til en høyere energitilstand,
2. fluorescens fører til en lavere energitilstand, og
3. skiftet i kjernekoordinater mellom bakken og opphisset tilstand indikerer en ny likevektsposisjon for kjernefysisk interaksjonspotensial. Det faktum at fluorescenspilen er kortere enn absorpsjonen indikerer at den har mindre energi, eller at bølgelengden er lengre.Den Klassiske Condon tilnærming Er antagelsen om at den elektroniske overgangen skjer på en tidsskala kort i forhold til kjernefysisk bevegelse, slik at overgangen sannsynligheten kan beregnes på en fast kjernefysisk posisjon.

   denne endringen i vibrasjon opprettholdes under en tilstand som kalles rask elektronisk eksitasjon. De resulterende Coulombiske kreftene gir en likevekt som vist i figuren for kjernene kalt et vendepunkt. Vendepunktet kan kartlegges ved å tegne en vertikal linje fra minimum av den nedre kurven til krysset mellom den høyere elektroniske tilstanden. Denne prosedyren kalles en vertikal overgang og ble diskutert før i sammenheng med fotoelektronspektroskopi (en annen elektronisk spektroscoy)..Franck-Condon-Prinsippet forklarer den relative intensiteten av vibroniske overganger ved å knytte sannsynligheten for en vibrasjonsovergang til overlappingen av vibrasjonsbølgefunksjonene. Det står at sannsynligheten for at en vibrasjonsovergang oppstår, er vektet Av Franck-Condon overlapping integral:

   \

   innenfor Franck-Condon-tilnærmingen betraktes kjernene som «faste» under elektroniske overganger. Dermed kan elektroniske overganger betraktes som vertikale overganger på elektroniske potensielle energikurver(vierical overganger I Figur \(\PageIndex{1}\)).

   Quantum Franck-Condon-Prinsippet

   Franck-Condon-Prinsippet har Både En Klassisk og Kvanteapplikasjon. Klassisk Er Franck-Condon-prinsippet tilnærmingen at en elektronisk overgang mest sannsynlig vil forekomme uten endringer i kjernens posisjoner i molekylærenheten og dens miljø. Den resulterende tilstanden kalles En Franck-Condon-tilstand, og overgangen involvert, en vertikal overgang. Den kvantemekaniske formuleringen av dette prinsippet er at intensiteten av en vibronisk overgang er proporsjonal med kvadratet av overlappingsintegralet mellom vibrasjonsbølgefunksjonene i de to tilstandene som er involvert i overgangen.Franck-Condon-prinsippet er basert på Born-Oppenheimer-tilnærmingen, som tillater separasjon av de elektroniske \(q\) og kjernefysiske \(Q\) bølgefunksjonene gitt den totale bølgefunksjonen.

   \

   siden overgangsoperatøren, \(\hat{\mu}(q)\), bare er avhengig av den elektroniske komponenten, kan de nukleære komponentene skilles fra overgangsmomentintegralet som dikterer sannsynligheten for at overgangen skjer:

   &= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{kjernefysisk overlapping}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}}/\psi_{el, i} \rangle \end{align}\]

   hvis kjerneoverlappingsintegralet er null for denne overgangen, vil overgangen ikke bli observert, uavhengig av størrelsen på den elektroniske faktoren.

   • \(S_{00}\) Overgang Evaluert Innen Harmonisk Oscillatormodell
   • \(S_{01}\) Overgang Evaluert Innen Harmonisk Oscillatormodell
   • Franck-Condon Progresjoner
   • Bidragsytere

   \(S_{00}\) Overgang Evaluert Innen Harmonisk Oscillatormodell

   kjernefysisk overlapping for null – nullovergangen \(S_{00}\) kan beregnes ganske enkelt ved å bruke definisjonen av Den gaussiske formen av harmoniske oscillatorbølgefunksjonene.

   nullpunktsbølgefunksjonen i bakken elektronisk tilstand er

   \

   \

   • \(\alpha=\dfrac{\sqrt{mk}}{\hbar}\)
   • \(r_e\) er likevektsbindingslengden i den elektroniske tilstanden

det kjernefysiske overlappende integralet er

\

eksponenten i ligningen\ (\ref{fc1}\) kan bli utvidet som

\

og vi bruker

\

\

for å erstatte og fullføre kvadratet inne i integralet. Vi kan uttrykke

\.\]

integralet i Ligningen \ (\ref{FC2}\) er

\

integralet er Et gaussisk integral. Du kan vise at hvis vi lar \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) så \(dz = \sqrt{\alpha} dR\) og integralet blir

\

Dette integralet er allerede løst, Fra en tabell med integraler, Blir Ligning \(\ref{FC3}\)

\

Vi Ville Følge Samme fremgangsmåte for å beregne at overlapping av zeroth nivå vibrasjon i bakken til den første opphisset vibrasjonsnivå av opphisset tilstand: \(s_{01}\).

\(S_{01}\) Overgang Evaluert Innen Harmonisk Oscillatormodell

for å beregne overlappingen av zeroth bakkenivå (\(v=0\)) med det første eksiterte tilstandsnivået (\(v’=1\)) bruker Vi Hermittpolynomet \(H_1 (x) =2x\) for å beskrive den eksiterte tilstandsbølgefunksjonen (se her for en gjennomgang av harmoniske oscillatorbølgefunksjoner). Her \(x = \ sqrt {\alpha} (R – Q_e)\).

\

med nullpunktsbølgefunksjonen i den elektroniske tilstanden i bakken er

\

den første eksiterte bølgefunksjonen i den eksiterte elektroniske tilstanden er

\

overlappingen av zeroth bakkenivå med det første opphissede tilstandsnivået (ligning \(\ref{fc01}\)) er da

\

\ \

de samme substitusjonene kan gjøres som ovenfor slik at integralet kan skrives som (ikke vist og til bli demonstrert i en lekser øvelser) og det endelige resultatet er

\

Vi kunne fortsette og beregne overlappingen av nullnivået i grunntilstanden med alle de høyere lysvibrasjonsnivåene: \(s_{02}\), \(s_{03}\), etc. Hvert begrep tilsvarer en overgang med en annen energi siden vibrasjonsnivåene har forskjellige energier. Absorpsjonsbåndet ser da ut som en progresjon (En Franck-Condon-progresjon) av overganger mellom forskjellige nivåer hver med sin egen sannsynlighet.

Franck-Condon Progresjoner

for å forstå betydningen av formelen ovenfor FOR FC faktor, la oss undersøke en bakken og opphisset tilstand potensiell energi overflate på \(T = 0\) Kelvin. Vist nedenfor er to tilstander atskilt med 8000 cm-1 i energi. Dette er energiseparasjon mellom bunnen av deres potensielle brønner, men også mellom de respektive nullpunktsenerginivåene. La oss anta at bølgetallet i vibrasjonsmodusen er 1,000 cm-1 og at bindingslengden økes på grunn av at et elektron fjernes fra en bindingsbane og plasseres i en anti-bindingsbane ved elektronisk eksitasjon.



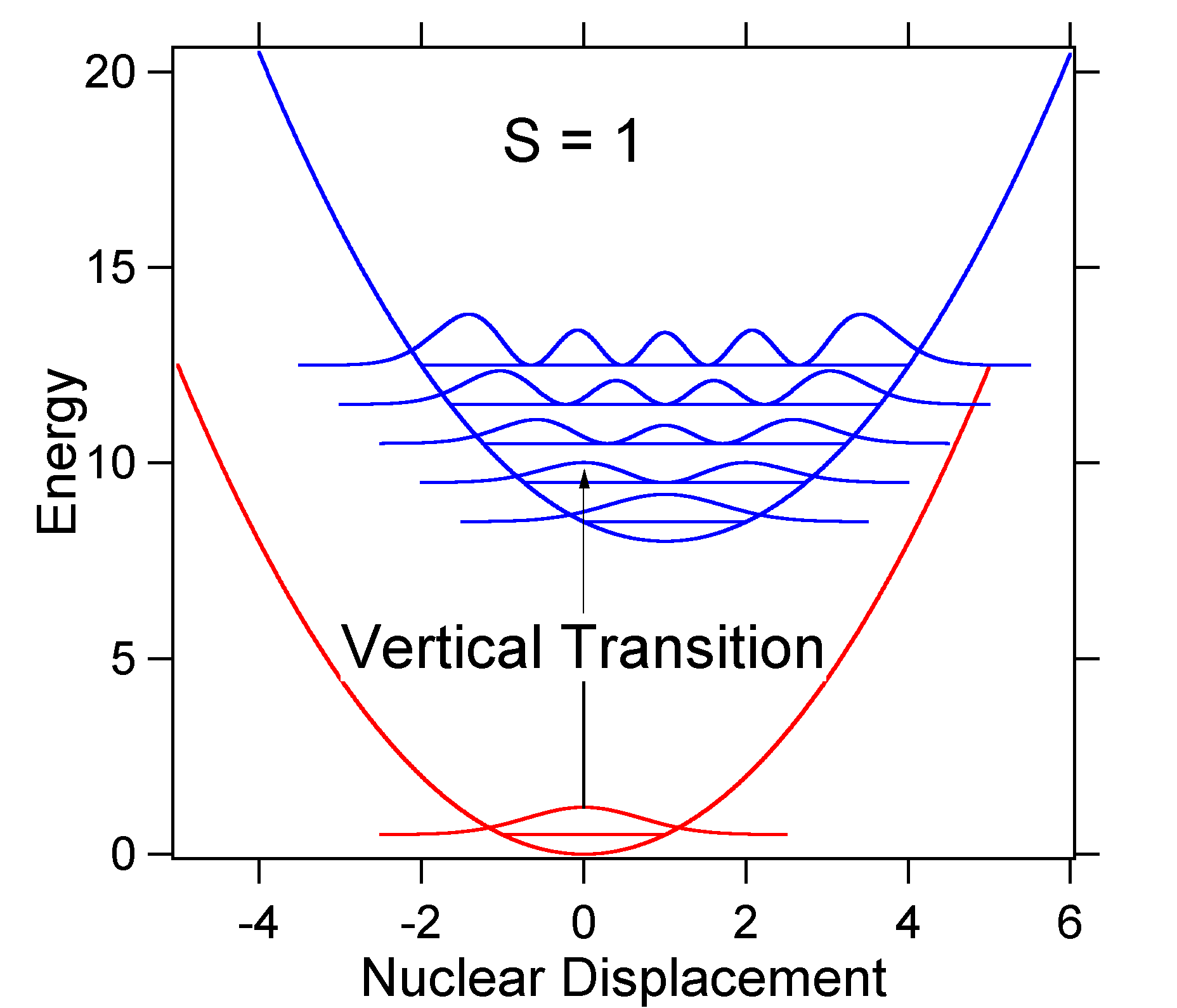
i Henhold til modellen ovenfor For Franck-Condon-faktoren vil vi generere et «pinne» – spektrum (Figur \(\PageIndex{3}\)) hvor hver vibrasjonsovergang er uendelig smal og overgang kan bare skje når \(E = h\nu\) nøyaktig. For eksempel ble de potensielle energiflatene gitt For S = 1 og overgangssannsynligheten på hvert nivå er gitt av pinnene (svart) i figuren nedenfor.



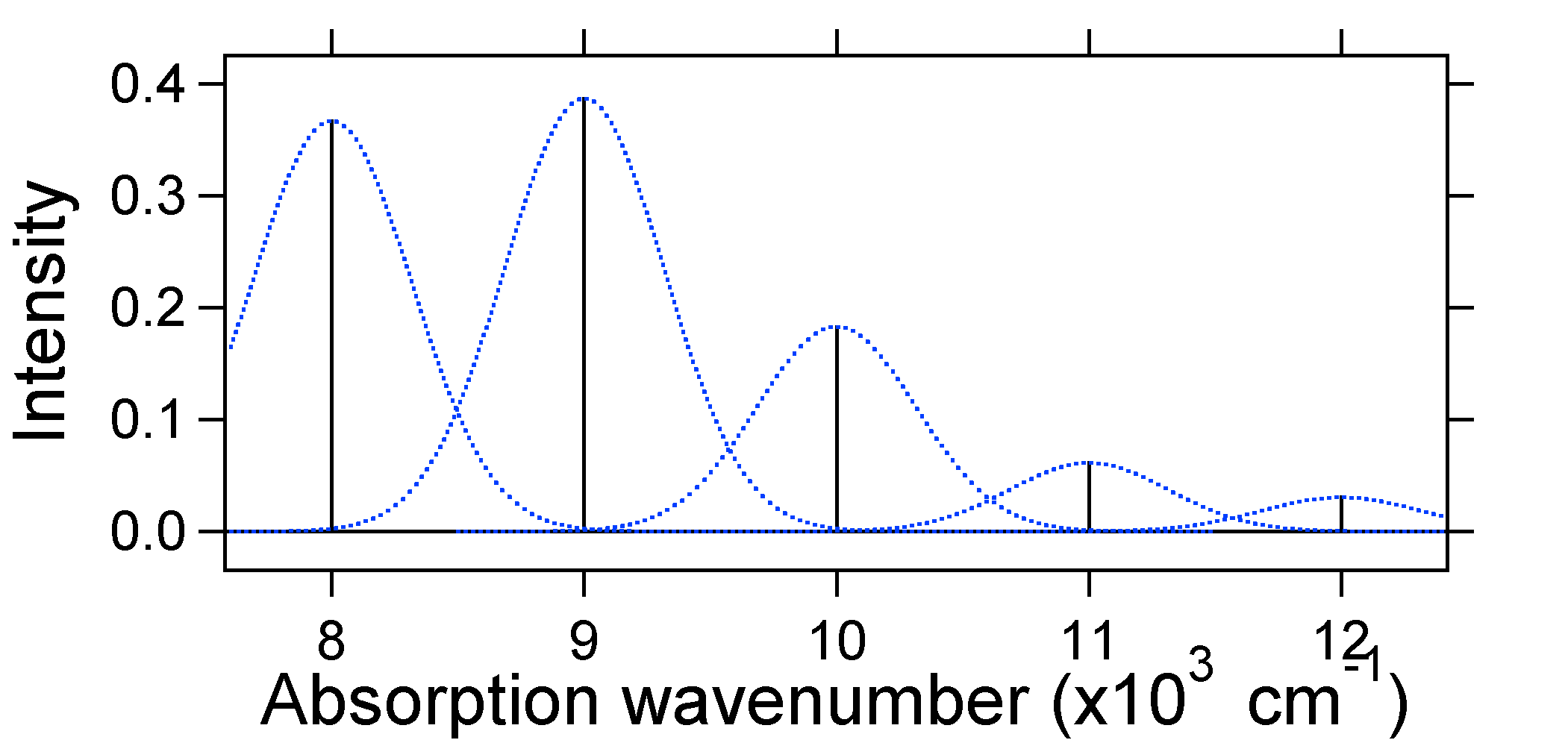
de stiplede Gausserne som omgir hver pinne gir et mer realistisk bilde av hvordan absorpsjonsspekteret skal se ut. I dette første stedet vil hvert energinivå (pinne) bli gitt litt bredde av det faktum at staten har en begrenset levetid. En slik utvidelse kalles homogen utvidelse siden den påvirker alle molekylene i ensemblet på lignende måte. Det er også utvidelse på grunn av små forskjeller i miljøet i hvert molekyl. Denne typen utvidelse kalles inhomogen utvidelse. Uavhengig av opprinnelse modellen ovenfor ble opprettet ved Hjelp Av En Gauss utvidelse

kjernefysisk forskyvning mellom bakken og opphisset tilstand bestemmer formen på absorpsjon spekteret. La oss undersøke både en mindre og en stor opphisset tilstand forskyvning. Hvis \(s=½\) og de potensielle energiflatene i dette tilfellet er:



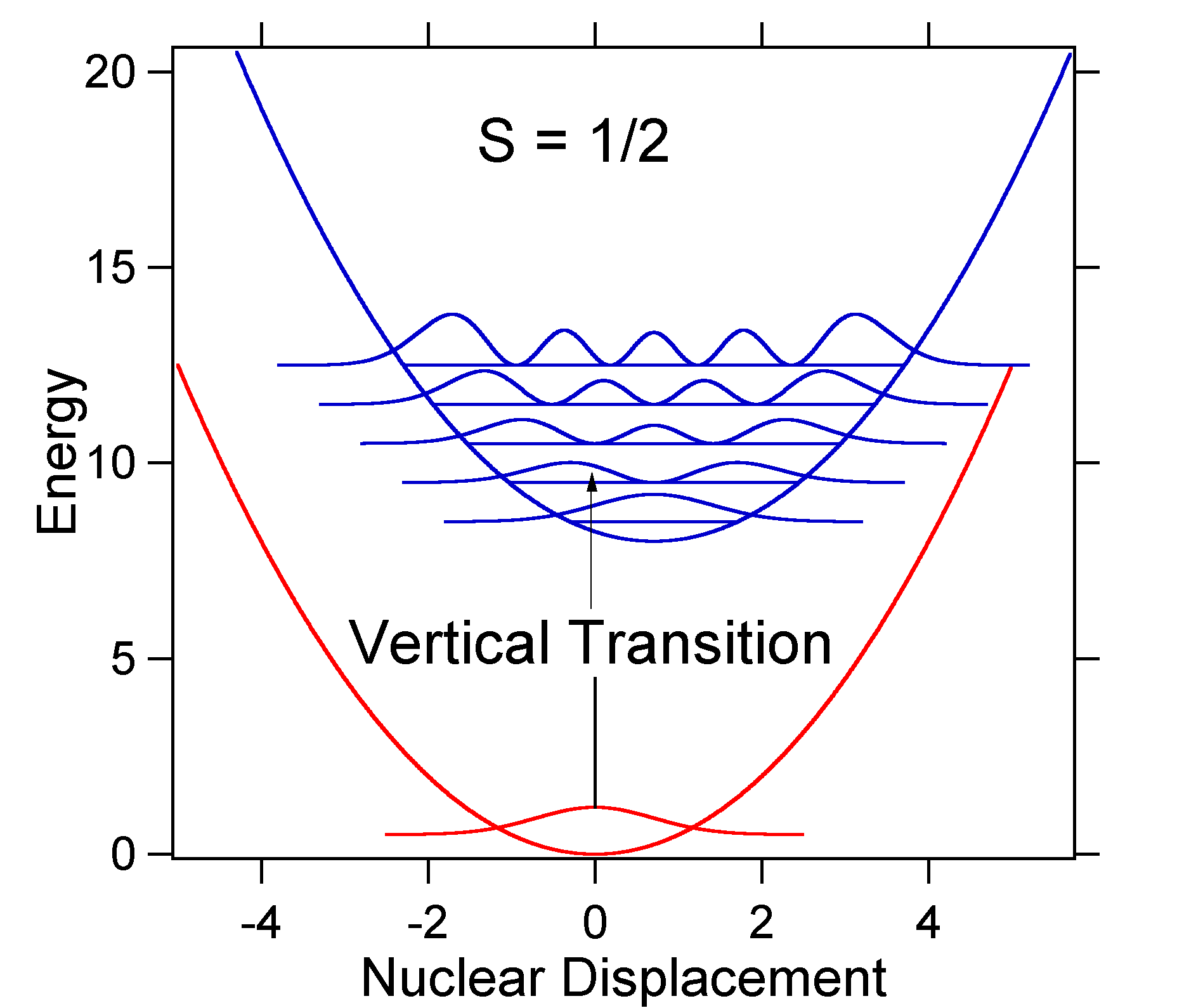
For this case the «stick» spectrum has the appearance in Figure \(\PageIndex{5}\)



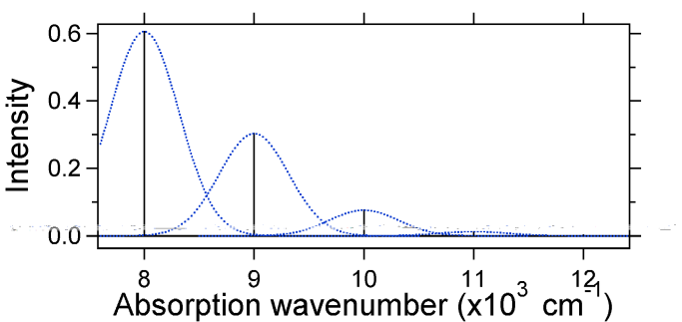
Merk at null-null eller \(S_{0,0}\) vibrasjonsovergang er mye stor i tilfelle hvor forskyvningen er liten.som en generell tommelfingerregel gir \(S\) konstanten forholdet mellom intensiteten av \(v = 2\) overgangen til \(v = 1\) overgangen. I dette tilfellet siden \(S = 0,5\) er\ (v=2\) overgangen 0,5 intensiteten av \(v=1\) overgang.

som et eksempel på en større forskyvning er disposisjonen av de potensielle energiflatene For S = 2 vist nedenfor.



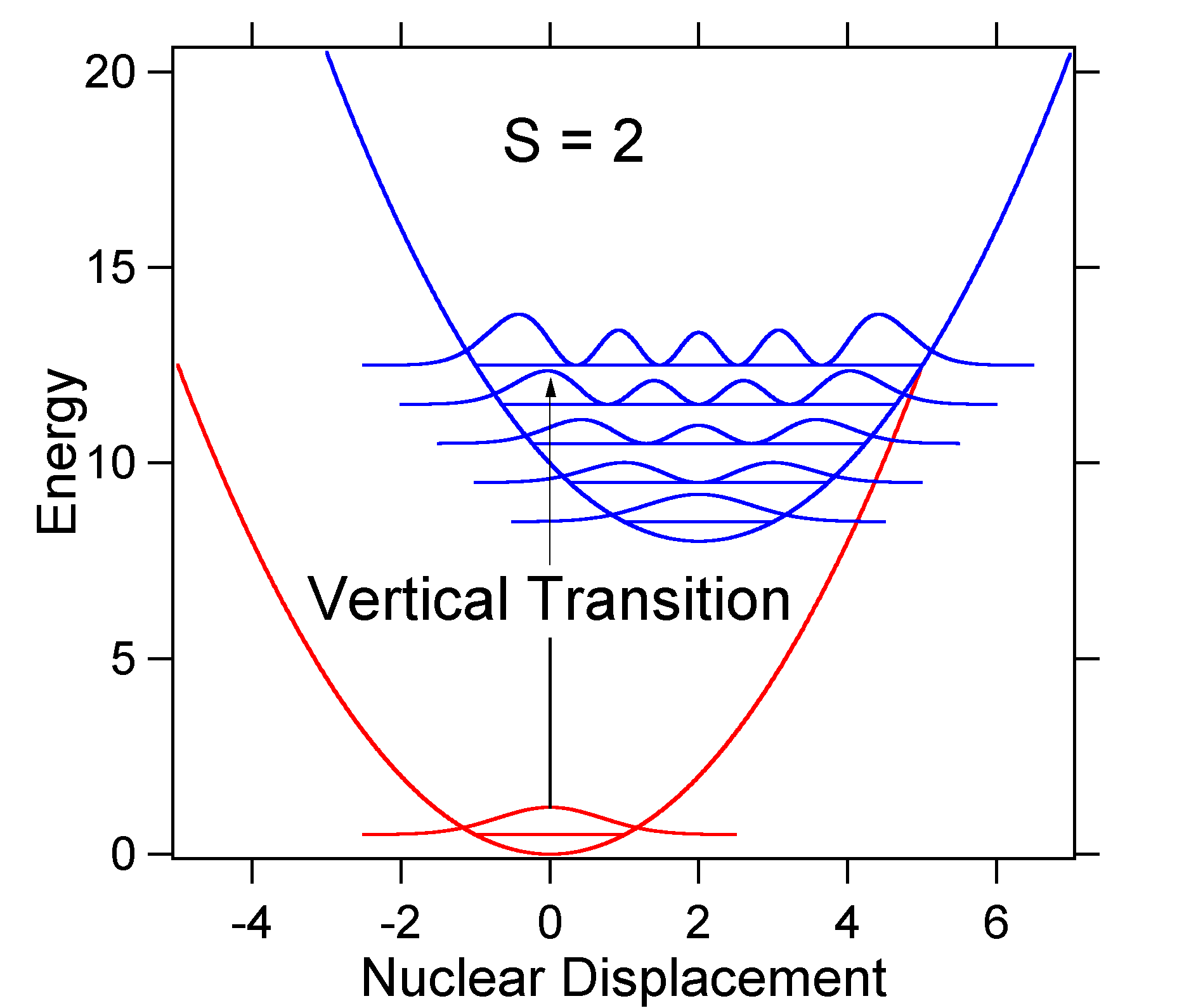
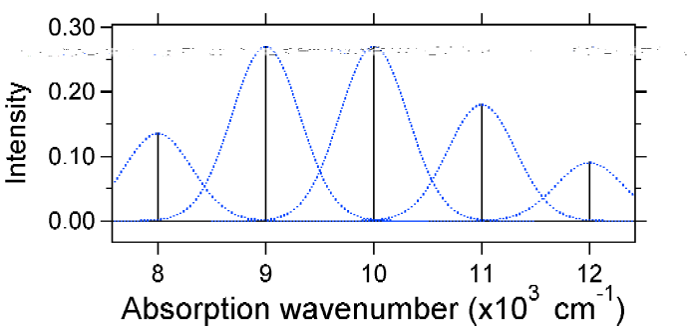
den større forskyvning resulterer i redusert overlapping av bakkenivå med v = 0 nivå av opphisset tilstand. Maksimal intensitet vil oppnås i høyere vibrasjonsnivåer som vist i stavspekteret.



absorpsjonsspektrene som er plottet nedenfor, har alle samme integrerte intensitet, men deres former endres på grunn av den forskjellige omfanget av forskyvning av den potensielle energioverflaten.



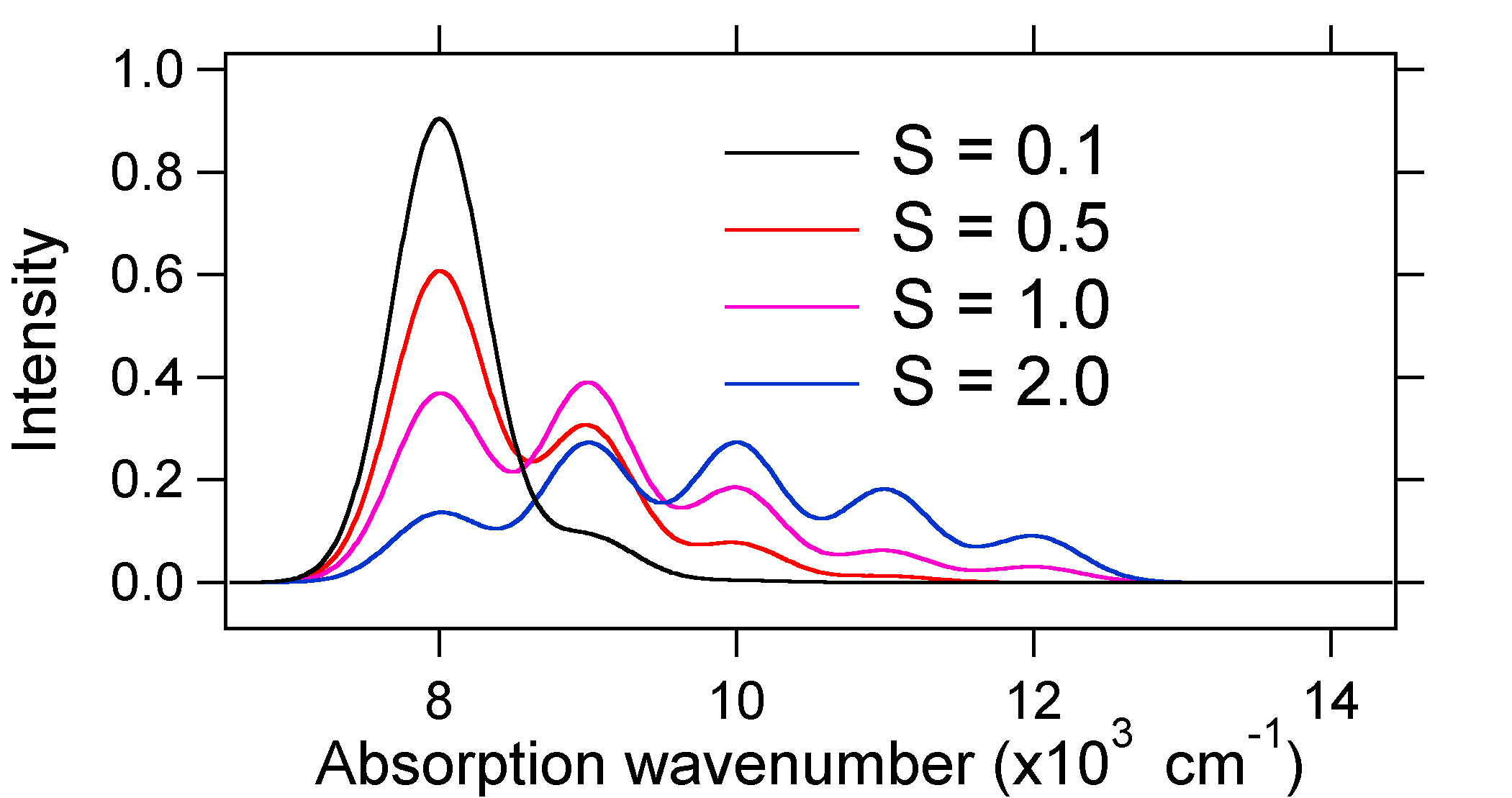
så naturen til de relative vibroniske båndintensitetene kan fortelle oss om det er en forskyvning av likevektskjernekoordinatet som fulgte en overgang. Når vil det være en økning i bond lengde (dvs. \(Q_e > R_e\))? Dette skjer når et elektron fremmes fra en bindingsmolekylær orbital til en ikke-binding eller anti-binding molekylære orbitaler (dvs.når bindingsordren er mindre i eksitert tilstand enn grunntilstanden).

• ikke-bonding molekylær orbital \(\rightarrow\) bonding molekylær orbital
• anti-bonding molekylær orbital
• Anti-bonding molekylær orbital \(\rightarrow\) ikke-bonding molekylær orbital

kort sagt, når bindingsordren er lavere i eksitert tilstand enn i grunntilstanden, så \(Q_e> r_e\); en okning i bondlength vil oppsta nar dette skjer.