Dyp Læring: Feed Forward Nevrale Nettverk (FFNNs)

Et Dypt Feed Forward Nevrale Nettverk (FFNN) — aka Flerlags Perceptron (MLP)

et kunstig nevralt nettverk (ann) er laget av mange sammenkoblede nevroner:

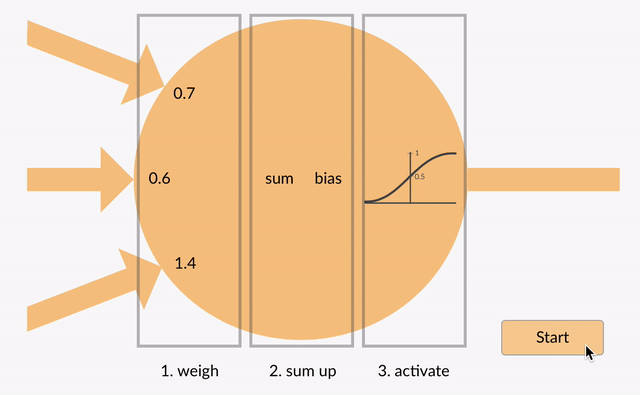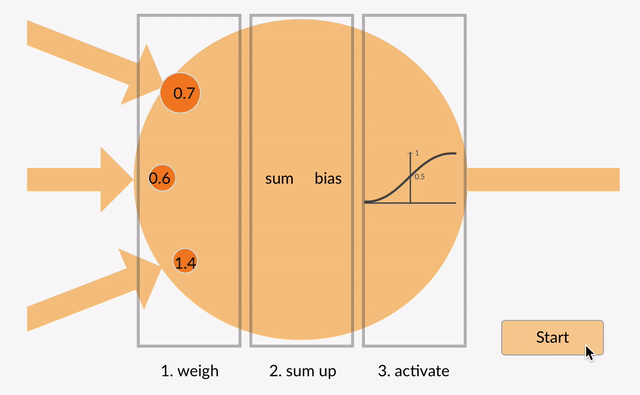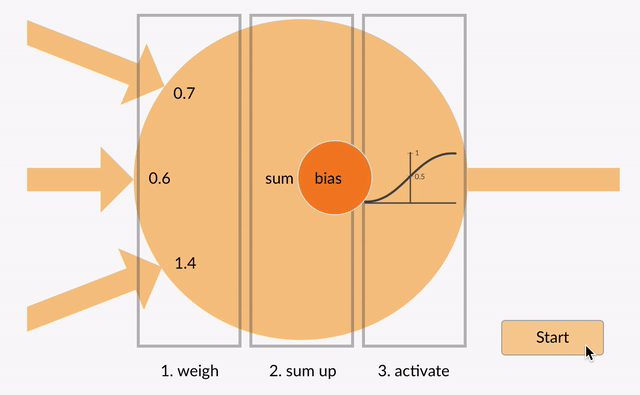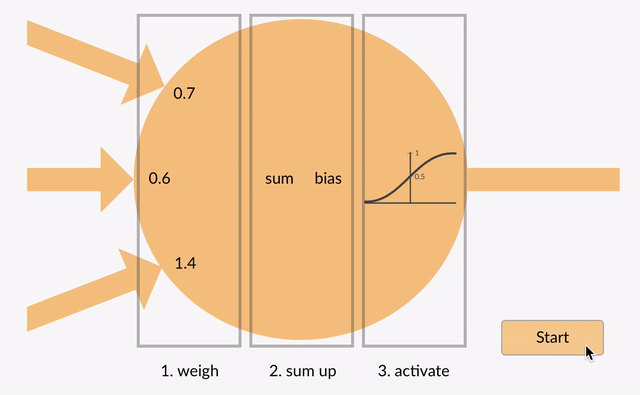
En enkelt neuron FRA et kunstig nevralt nettverk (ann)

hver nevron tar i noen flytende punkt tall (f.eks 1.0, 0.5, -1.0) og multipliserer dem med noen andre flytende punkt tall (f. eks 0,7, 0,6, 1,4) kjent som vekter (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Vektene fungere som en mekanisme for å fokusere på, eller ignorere, visse innganger.

Vekter fungerer som myke porter for å ignorere noen funksjoner (0) og fokuser på andre (+1) eller til og med hemme dem (-1)

de vektede inngangene blir så summert sammen (f. eks. 0.7 + 0.3 + -1.4 = -0.4) sammen med en bias verdi (f. eks -0,4 + -0,1 = -0,5).

den summerte verdien (x) blir nå omdannet til en utgangsverdi (y) i henhold til nevronets aktiveringsfunksjon (y = f(x)). Noen populære aktiveringsfunksjoner er vist nedenfor:

et lite utvalg Av Populære Aktiveringsfunksjoner

f.eks. -0.5 → -0.05 hvis vi bruker leaky rectified linear unit (leaky relu) aktiveringsfunksjon: y = f(x) = f(-0,5) = max(0,1*-0,5, -0,5) = max(-0,05, -0,5) = -0.05

neurons utgangsverdi (f. eks. -0,05) er ofte en inngang for et annet neuron.

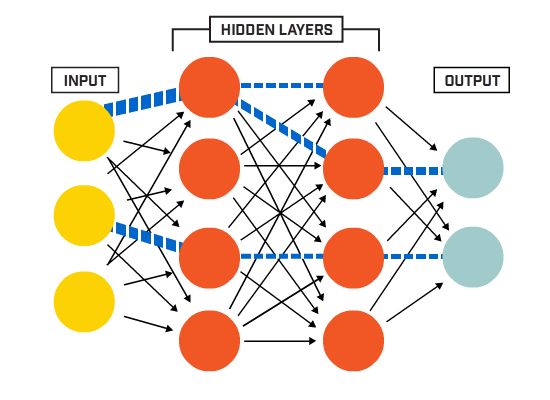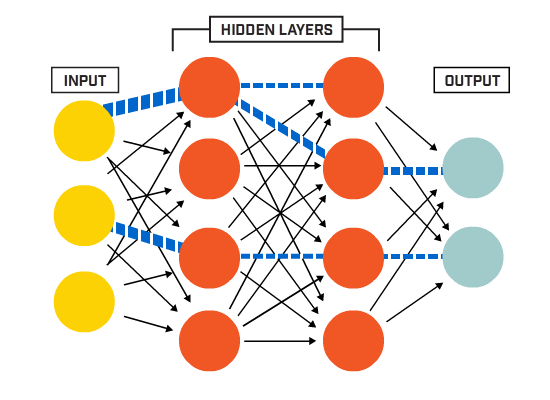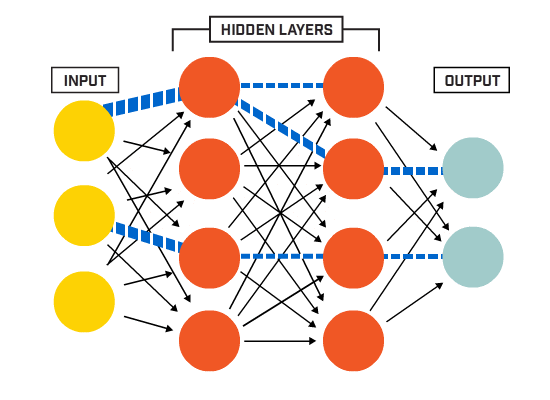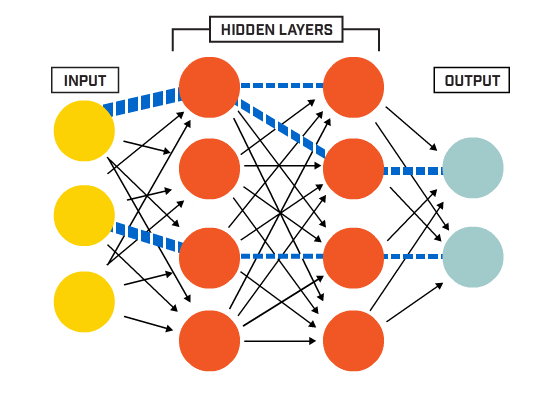
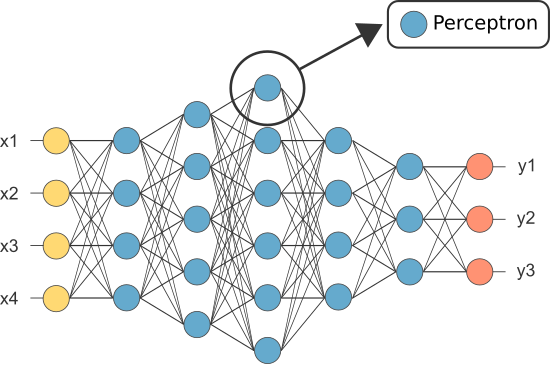
En Neurons utgangsverdi strømmer ofte inn som en inngang til andre Nevroner I DET Kunstige Nevrale Nettverket (ANN)

perceptronen, et Av De Første Nevrale Nettverkene, er laget av bare en enkelt nevron

imidlertid var en av de første annene kjent som perceptronen, og den besto av av bare en enkelt neuron.

utgangen av perceptronens (eneste) neuron fungerer som den endelige prediksjonen.

Hver Nevron er en lineær binær klassifikator alt på egen hånd (f. eks. en utgangsverdi >= 0 indikerer den blå klassen, mens en utgangsverdi < 0 indikerer den røde klassen)

lar kode vår egen perceptron:

import numpy as npclass Neuron: 
def __init__(self, n_inputs, bias = 0., weights = None): 
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs): 
return self._f(xs @ self.ws + self.b) 
def _f(self, x): 
return max(x*.1, x)

(Merk: vi har ikke tatt med noen læringsalgoritme i vårt eksempel ovenfor — vi skal dekke læringsalgoritmer i en annen opplæring)

perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

legg merke til at ved å justere verdiene til vekter og bias, kan Du justere nevronens beslutningsgrense. (NB: en nevron lærer ved å oppdatere sine vekter og biasverdier for å redusere feilen i sine beslutninger).

så hvorfor trenger vi så mange nevroner i EN ANN hvis noen vil være tilstrekkelig (som klassifiserer)?

Begrensninger: nevronen er en binær klassifikator siden den bare kan lære å skille mellom to klasser (f.eks. blå og rød) maks. Nevronet er en lineær klassifikator fordi det er beslutningsgrense tilnærmet til en rett linje FOR 2D-data (eller et flatt plan FOR 3d-data, etc)

Dessverre kan individuelle nevroner bare klassifisere lineært separerbare data.

men ved å kombinere nevroner sammen, kombinerer vi i hovedsak deres beslutningsgrenser. DERFOR ER EN ANN sammensatt av mange nevroner i stand til å lære komplekse, ikke-lineære beslutningsgrenser.

Kombinere Nevroner gjør At Nevrale Nettverk kan lære mer komplekse, Ikke-Lineære Beslutningsgrenser

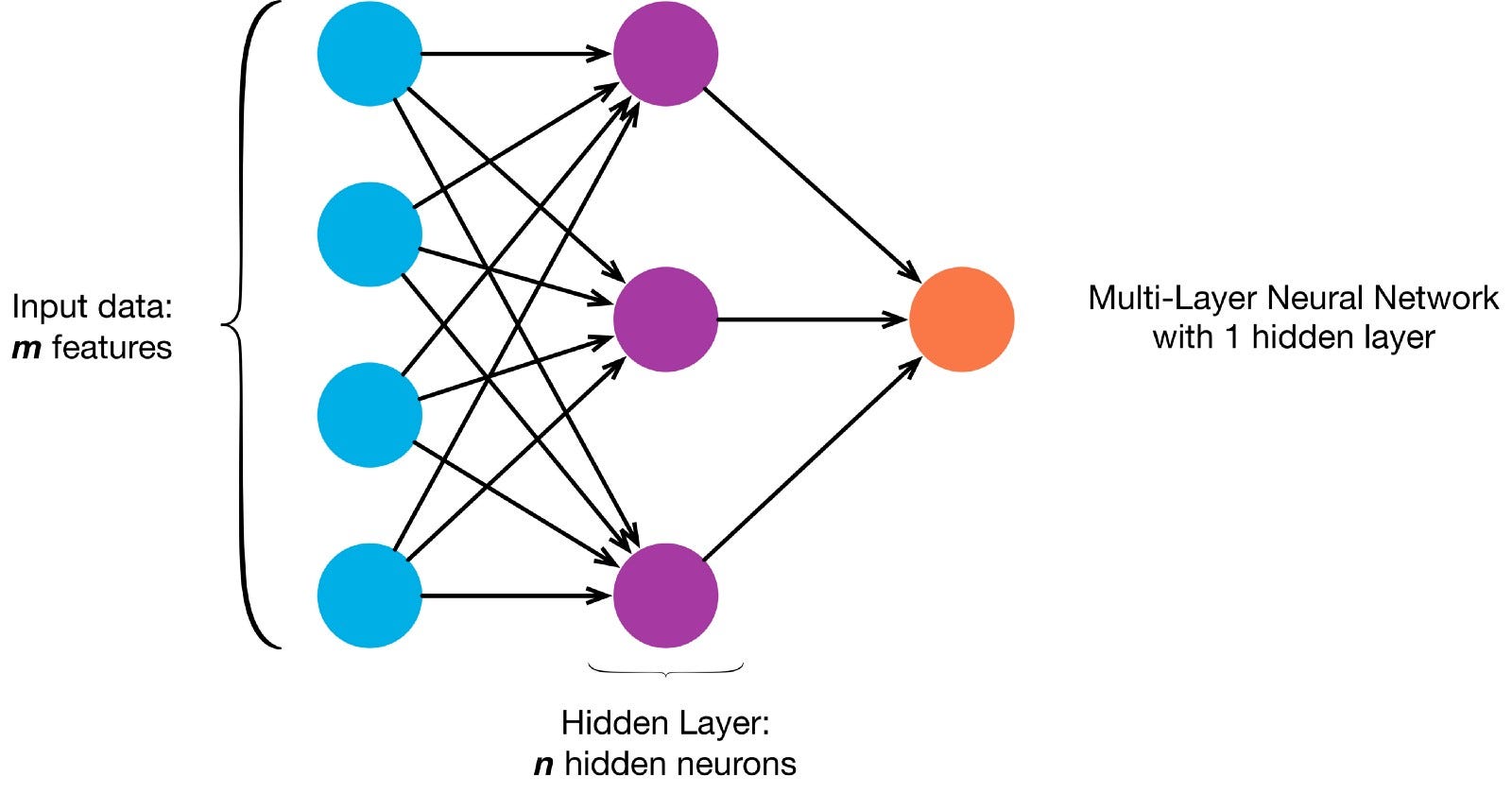
Nevroner er koblet sammen i henhold til en bestemt nettverksarkitektur. Selv om det er forskjellige arkitekturer, inneholder nesten alle lag. (NB: Nevrale Nettverk inneholder Lag

Det er typisk et inngangslag (som inneholder en rekke nevroner). antall inngangsfunksjoner i dataene), et utgangslag (som inneholder et antall nevroner lik antall klasser) og et skjult lag (som inneholder et hvilket som helst antall nevroner).

Dype nevrale nettverk inneholder flere skjulte lag

det kan være mer enn ett skjult lag for å la det nevrale nettet lære mer komplekse beslutningsgrenser (noen nevrale nettverk).net med mer enn ett skjult lag regnes som et dypt nevralt nett).

Lar bygge en dyp NN å male dette bildet:

et eksempelbilde SOM vår ANN vil lære å male (det vil lære å knytte bestemte farger til bestemte regioner i bildet)

lar nedlasting i en matrise

!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)

nå lærer vår ann å male er en overvåket læringsoppgave, så vi må lage et merket treningssett (våre treningsdata vil ha innganger og forventede UTDATAETIKETTER for hver inngang). Treningsinngangene vil ha 2 verdier (x, y koordinatene til hver piksel).

Gitt enkelheten i bildet, kan vi faktisk nærme seg dette problemet på en av to måter. Et klassifikasjonsproblem (hvor nevrale nettet forutsier om en piksel tilhører den» blå «klassen eller den» grå » klassen, gitt xy-koordinatene) eller et regresjonsproblem(hvor nevrale nettet forutsier RGB-verdier for en piksel gitt koordinatene).

hvis du behandler dette som et regresjonsproblem: treningsutgangene vil ha 3 verdier (de normaliserte r,g,b-verdiene for hver piksel). – Kan bruke denne metoden for nå.

training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))

nå kan lage VÅR ANN:

et fullt tilkoblet feed-forward nevralt nettverk (FFNN)-aka en flerskikts perceptron (ffnn) mlp)

det skal ha 2 nevroner i inngangslaget (siden det er 2 verdier å ta inn: x & y koordinater).
Det skal ha 3 nevroner i utgangslaget (siden det er 3 verdier å lære: r, g, b).jeg vil bruke 10 skjulte lag med 100 nevroner i hvert skjult lag (noe som gjør dette til et dypt nevralt nettverk)

from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)

det trente nettverket kan nå forutsi de normaliserte rgb — verdiene for eventuelle koordinater (dette vil si at det ikke er nok). f. eks. x, y = 1,1).

ann.predict(])

array(])

lar BRUKE ANN å forutsi rgb verdier for hver koordinat og lar vise spådd rgb verdier for hele bildet for å se hvor godt det gjorde (kvalitativt — vi skal forlate evaluering beregninger for en annen tutorial)

predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array = 
i += 1
Image.fromarray(predicted_image_array)

prøv å endre hyperparametrene for å få bedre resultater.Hvis vi i stedet for å behandle dette som et regresjonsproblem, behandler dette som et klassifiseringsproblem, vil treningsutgangene ha 2 verdier (sannsynlighetene for pikselen som tilhører hver av de to klassene: «blå» og «grå»)

training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)

VI kan gjenoppbygge VÅR ANN som en binær klassifikator med 2 nevroner i inngangslaget, 2 nevroner i utgangslaget og 100 nevroner i det skjulte laget (med 10 skjulte lag)

from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)

vi kan nå bruke den trente ann å forutsi klassen som hver piksel tilhører (0: «grå» eller 1: «blå»). The argmax function is used to find which class has the highest probability

np.argmax(ann.predict(]))

(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: «grey»)

predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array = 
else:
predicted_image_array = 
i += 1
Image.fromarray(predicted_image_array)

Legg igjen en kommentar Avbryt svar