Forstå Deep Residual Networks

Deep residual networks (ResNet) tok deep learning verden med storm Når Microsoft Research utgitt Deep Residual Learning For Bildegjenkjenning. Disse nettverkene førte til 1. plass vinnende oppføringer i alle fem hovedspor Av ImageNet og COCO 2015 konkurranser, som dekket bilde klassifisering, objekt deteksjon, og semantisk segmentering. Robustheten Til ResNets har siden blitt bevist av ulike visuelle gjenkjenningsoppgaver og av ikke-visuelle oppgaver som involverer tale og språk. Jeg brukte Også ResNet i tillegg til andre dype læringsmodeller i Min Doktorgradsavhandling.

dette innlegget vil oppsummere de tre papirene nedenfor, som alle er skrevet eller co-skrevet Av Resnets oppfinner Kaiming He, fordi jeg tror de opprinnelige papirene gir den mest intuitive og detaljerte forklaringen av modellen / nettverkene. Forhåpentligvis kan dette innlegget hjelpe deg med å få en bedre forståelse av kjernen i gjenværende nettverk.

• Dyp Restlæring for Bildegjenkjenning
• Identitetstilordninger I Dype Restnettverk
• Aggregert Resttransformasjon For Dype Nevrale Nettverk

Intuisjon på Dypt Restnettverk (stackoverflow ref)

en restblokk vises som følgende:

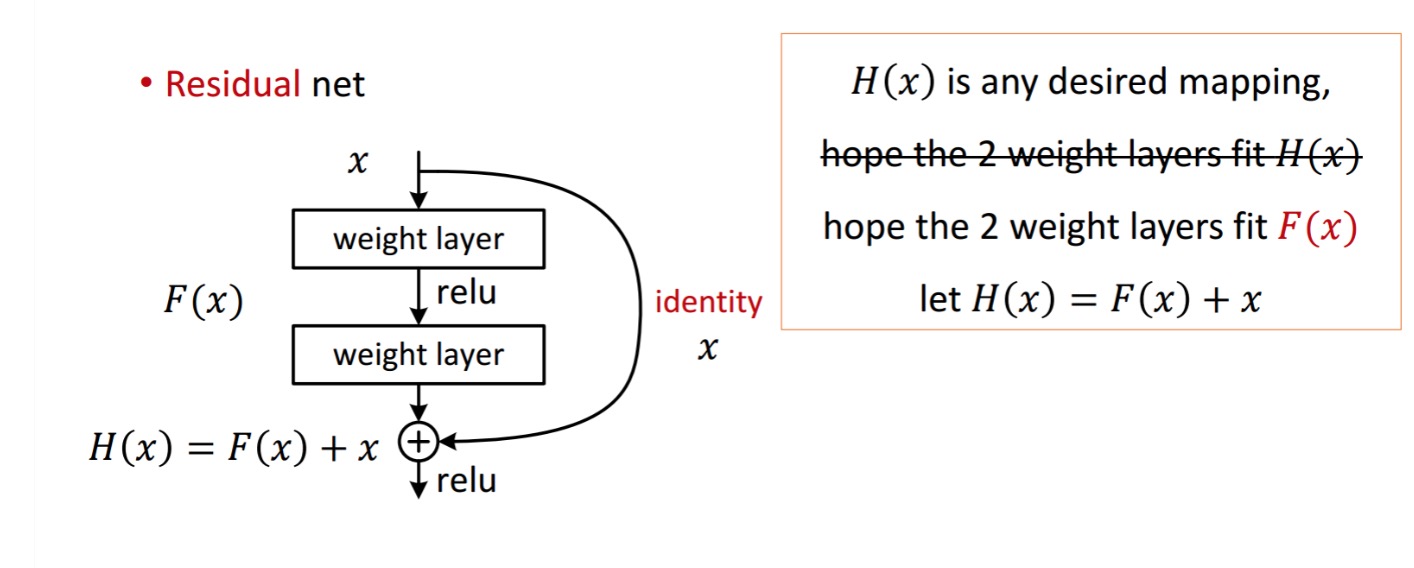
så den gjenværende enheten som vises, oppnås ved behandling Med To Vektlag. Deretter legger det til for a oppna . Nå, anta at er din ideelle spådd utgang som samsvarer med bakken sannheten. Siden, å oppnå ønsket avhenger av å få det perfekte . Det betyr at de to vektlagene i restenheten faktisk skal kunne produsere ønsket , så får det ideelle garantert.

er hentet fra som følger.

er hentet fra som følger.

forfatterne hypoteser at gjenværende kartlegging (dvs.) kan være lettere å optimalisere enn . For å illustrere med et enkelt eksempel, anta at det ideelle . Så for en direkte kartlegging ville det være vanskelig å lære en identitetskartlegging, da det er en stabel med ikke-lineære lag som følger.

Så, for å tilnærme identitetskartleggingen med alle disse vekter og ReLUs i midten ville det være vanskelig.

Nå, hvis vi definerer ønsket kartlegging, må vi bare få som følger.

Å Oppnå det ovenfor er enkelt. Bare sett noen vekt til null, og du vil få en null utgang. Legg tilbake og du får ønsket kartlegging.

Dyp Gjenværende Læring for Bildegjenkjenning

Problem

når dypere nettverk begynner å konvergere, har et nedbrytningsproblem blitt utsatt: med nettverksdybden økende, blir nøyaktigheten mettet og degraderes raskt.

Se Nedverdigende I Aksjon:

La oss ta et grunt nettverk og dets dypere motstykke ved å legge til flere lag til det.

Worst case scenario: Deeper modells tidlige lag kan erstattes med grunt nettverk, og de resterende lagene kan bare fungere som en identitetsfunksjon (Inngang lik utgang).

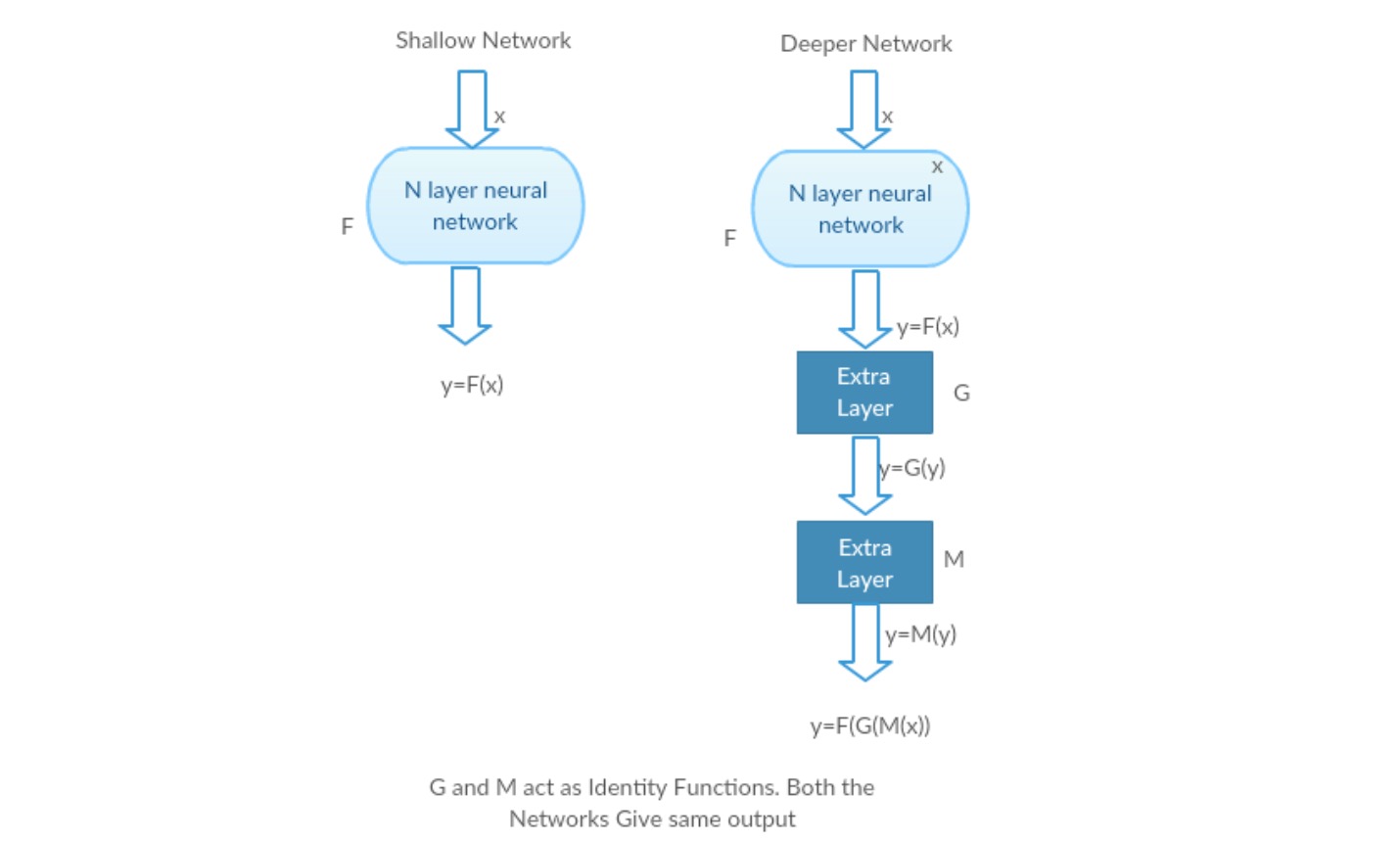
Givende scenario: i det dypere nettverket tilnærmer de ekstra lagene bedre kartleggingen enn det er grunnere tellerdel og reduserer feilen med en betydelig margin.

Eksperiment: I verste fall bør både det grunne nettverket og dypere varianten av det gi samme nøyaktighet. I det givende scenariet skal den dypere modellen gi bedre nøyaktighet enn den er grunne tellerdelen. Men eksperimenter med våre nåværende løsere avslører at dypere modeller ikke fungerer bra. Så bruk av dypere nettverk er nedverdigende ytelsen til modellen. Disse papirene prøver å løse dette problemet Ved Hjelp Av Deep Residual learning framework.

hvordan løse?

I Stedet for å lære en direkte kartlegging av med en funksjon(noen stablet ikke-lineære lag). La oss definere restfunksjonen ved hjelp av , som kan reframed inn , hvor og representerer de stablede ikke-lineære lagene og identitetsfunksjonen(input=output) henholdsvis.

forfatterens hypotese er at det er lett å optimalisere restkartleggingsfunksjonen enn å optimalisere den opprinnelige, ikke-refererte kartleggingen .

Intuisjon bak Gjenværende blokker:

La oss ta identitetskartleggingen som et eksempel (f.eks.). Hvis identitetskartleggingen er optimal, kan vi enkelt skyve residualene til null () enn å passe til en identitetskartlegging () med en stabel med ikke-lineære lag. På enkelt språk er det veldig enkelt å komme opp med en løsning som i stedet for å bruke stabel med ikke-lineære cnn-lag som funksjon (Tenk på det). Så, denne funksjonen er hva forfatterne kalte Gjenværende funksjon.

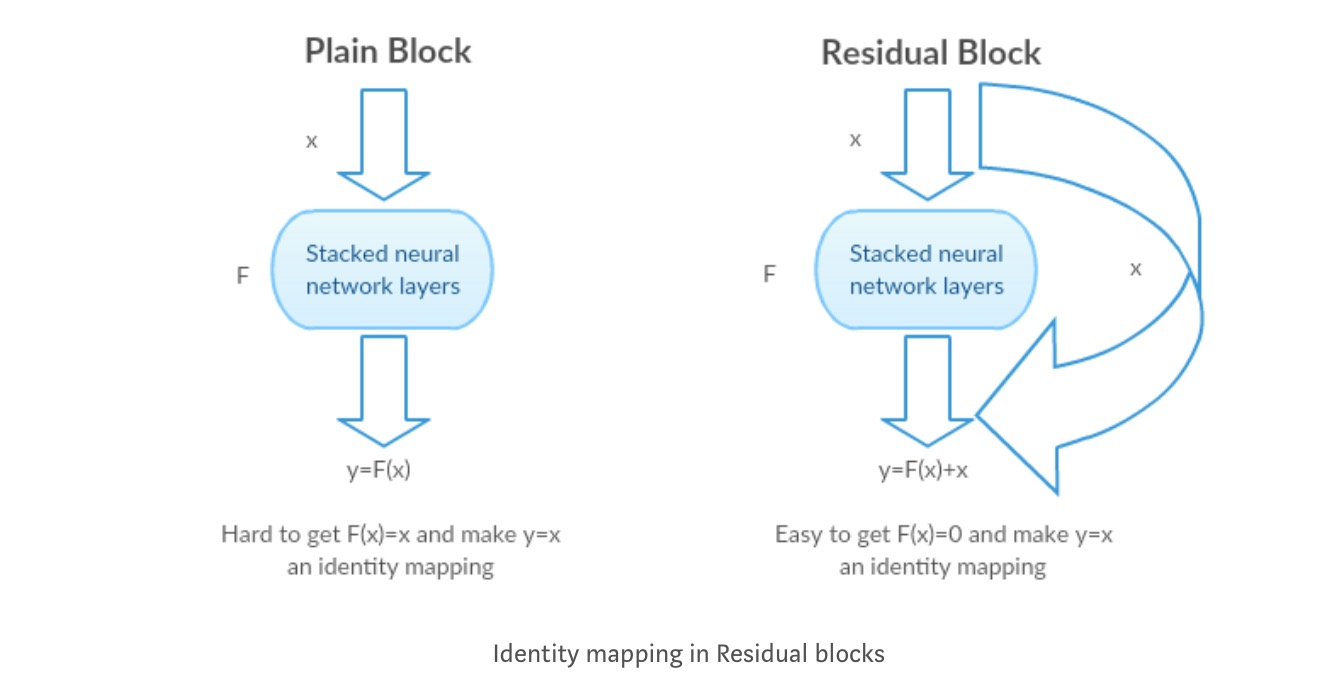
forfatterne gjorde flere tester for å teste deres hypotese. La oss se på hver av dem nå.

Testtilfeller:

Ta et vanlig nettverk (VGG kind 18 layer network) (Nettverk-1) og en dypere variant av det (34-lag, Nettverk-2) og legg Til Gjenværende lag I Nettverket-2(34 lag med gjenværende tilkoblinger, Nettverk-3).

Designe nettverket:

1. Bruk 3 * 3 filtre for det meste.
2. Ned sampling MED CNN lag med stride 2.
3. Globalt gjennomsnittslag og et 1000-veis fullt tilkoblet lag med Softmax til slutt.

det finnes to typer restforbindelser:

I. identitetsnarveiene () kan brukes direkte når inngang () og utgang () er av samme dimensjoner.

II. NÅR dimensjonene endres, a) utfører snarveien fortsatt identitetskartlegging, med ekstra nulloppføringer polstret med den økte dimensjonen. B) projeksjonsnarveien brukes til å matche dimensjonen (gjort av 1 * 1 conv) ved hjelp av følgende formel

Resultater

Selv om 18-lagsnettverket bare er underrommet i 34-lagsnettverket, fungerer det fortsatt bedre. ResNet overgår med en betydelig margin i tilfelle nettverket er dypere

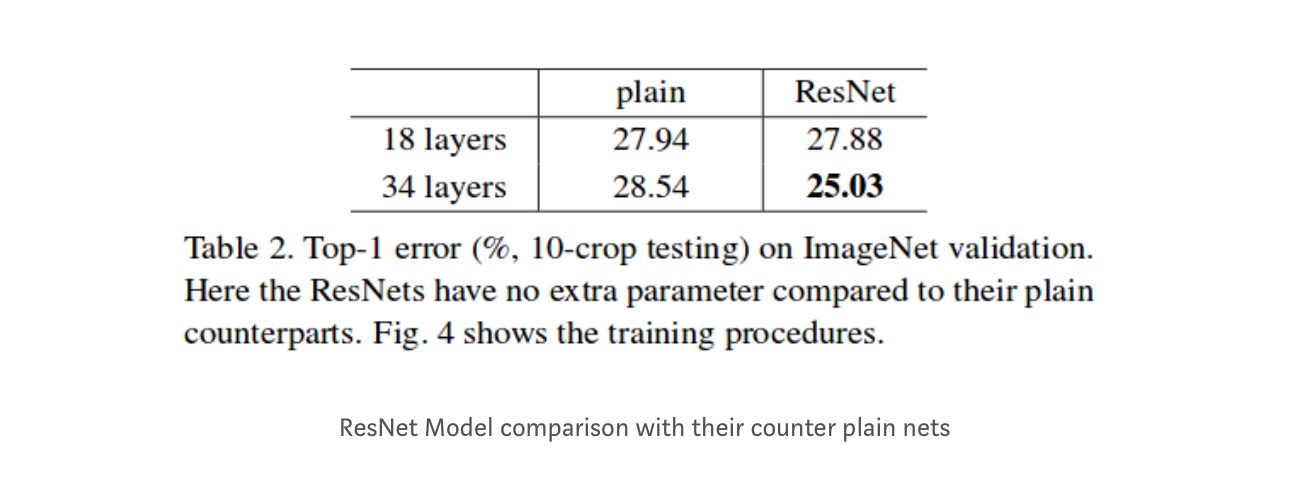
Dypere studier

videre studeres flere nettverk:

Hver ResNet-blokk er enten 2 lag dyp (brukes i små nettverk som resnet 18, 34) eller 3 lag dyp( resnet 50, 101, 152).

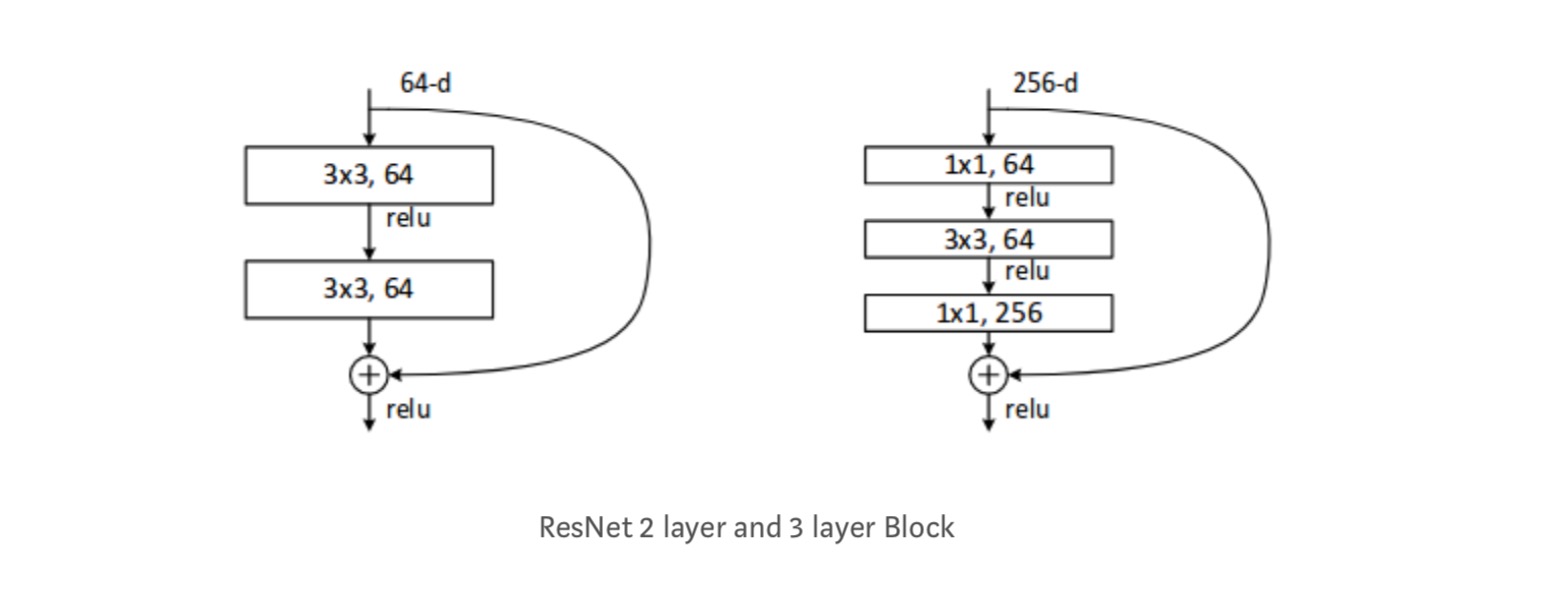
Observasjoner

1. ResNet-Nettverket Konvergerer raskere sammenlignet med vanlig tellerdel av Det.
2. Identitet vs Projeksjon shorcuts. Svært små inkrementelle gevinster ved hjelp av projeksjonsgenveier (Ligning-2) i alle lagene. Så alle ResNet-blokker bruker Bare Identitetsnarveier med Projeksjonsnarveier som bare brukes når dimensjonene endres.
3. ResNet-34 oppnådde en topp-5 valideringsfeil på 5,71% bedre ENN BN-inception og VGG. ResNet-152 oppnår en topp-5 valideringsfeil på 4,49%. Et ensemble på 6 modeller med forskjellige dybder oppnår en topp – 5 valideringsfeil på 3,57%. Vinne 1. plass I ILSVRC-2015

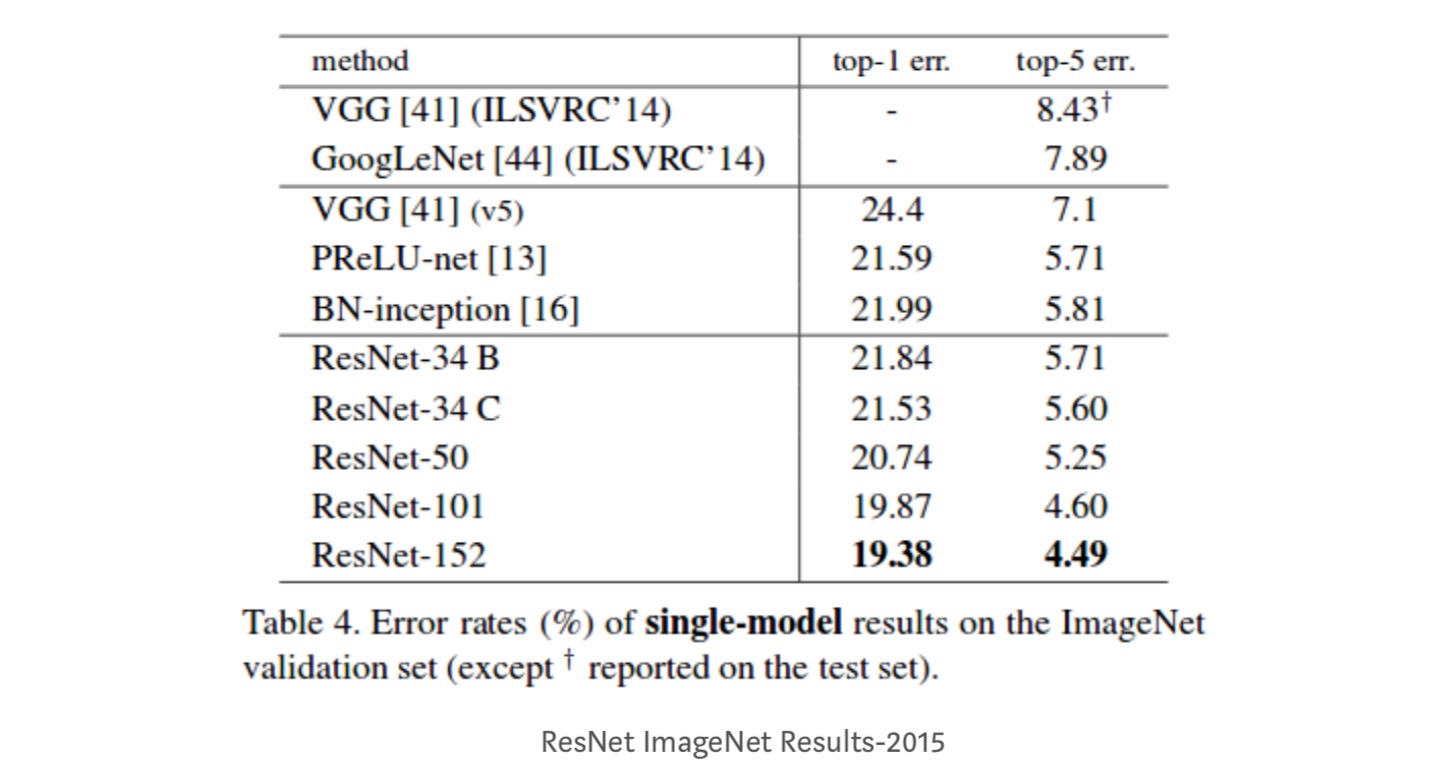
Identity mappings In Deep Residual Networks

dette papiret gir den teoretiske forståelsen av hvorfor forsvinnende gradientproblem ikke er tilstede I Restnettverk og rollen som hopp over tilkoblinger (hopp over tilkoblinger betyr inngangen eller ) ved å erstatte Identitetskartlegging (x) med forskjellige funksjoner.

Innledning

Dype restnett består av mange stablede «Restenheter». Hver enhet kan uttrykkes i en generell form:

hvor og er inngang og utgang av enheten, og er en gjenværende funksjon. I det siste papiret, er en identitetskartlegging og er En ReLU-funksjon.

Den sentrale ideen Med ResNets er å lære den additive restfunksjonen i forhold til, med et sentralt valg av å bruke en identitetskartlegging . Dette realiseres ved å legge ved en identity skip-tilkobling («snarvei»).

i dette papiret analyserer vi dype gjenværende nettverk ved å fokusere på å skape en «direkte» bane for å spre informasjon — ikke bare innenfor en gjenværende enhet, men gjennom hele nettverket. Våre avledninger avslører at hvis begge og er identitetskartlegginger, kan signalet overføres direkte fra en enhet til andre enheter, både i forover og bakover. Våre eksperimenter viser empirisk at trening generelt blir lettere når arkitekturen er nærmere de to ovennevnte forholdene.

for å forstå rollen som hopp over tilkoblinger, analyserer og sammenligner vi ulike typer . Vi finner at identitetskartleggingen som er valgt i det siste papiret, oppnår den raskeste feilreduksjonen og laveste treningstap blant alle varianter vi undersøkte, mens hopp over tilkoblinger av skalering , gating og 1×1-omveltninger alle fører til høyere treningstap og feil. Disse forsøkene tyder på at det å holde en» ren » informasjonsbane er nyttig for å lette optimalisering.

for å konstruere en identitetskartlegging , ser vi aktiveringsfunksjonene (ReLU og BN) som » forhåndsaktivering «av vektlagene, i motsetning til konvensjonell visdom av»etteraktivering». Dette synspunktet fører til en ny restenhetsdesign, vist i figuren nedenfor. Basert på denne enheten presenterer vi konkurransedyktige resultater PÅ CIFAR-10/100 med Et 1001-lags ResNet, som er mye lettere å trene og generaliserer bedre enn det opprinnelige ResNet. Vi rapporterer videre forbedrede resultater på ImageNet ved hjelp av et 200-lags ResNet, som motstykket til det siste papiret begynner å overfit. Disse resultatene tyder på at det er mye plass til å utnytte dimensjonen av nettverksdybde, en nøkkel til suksessen til moderne dyp læring.

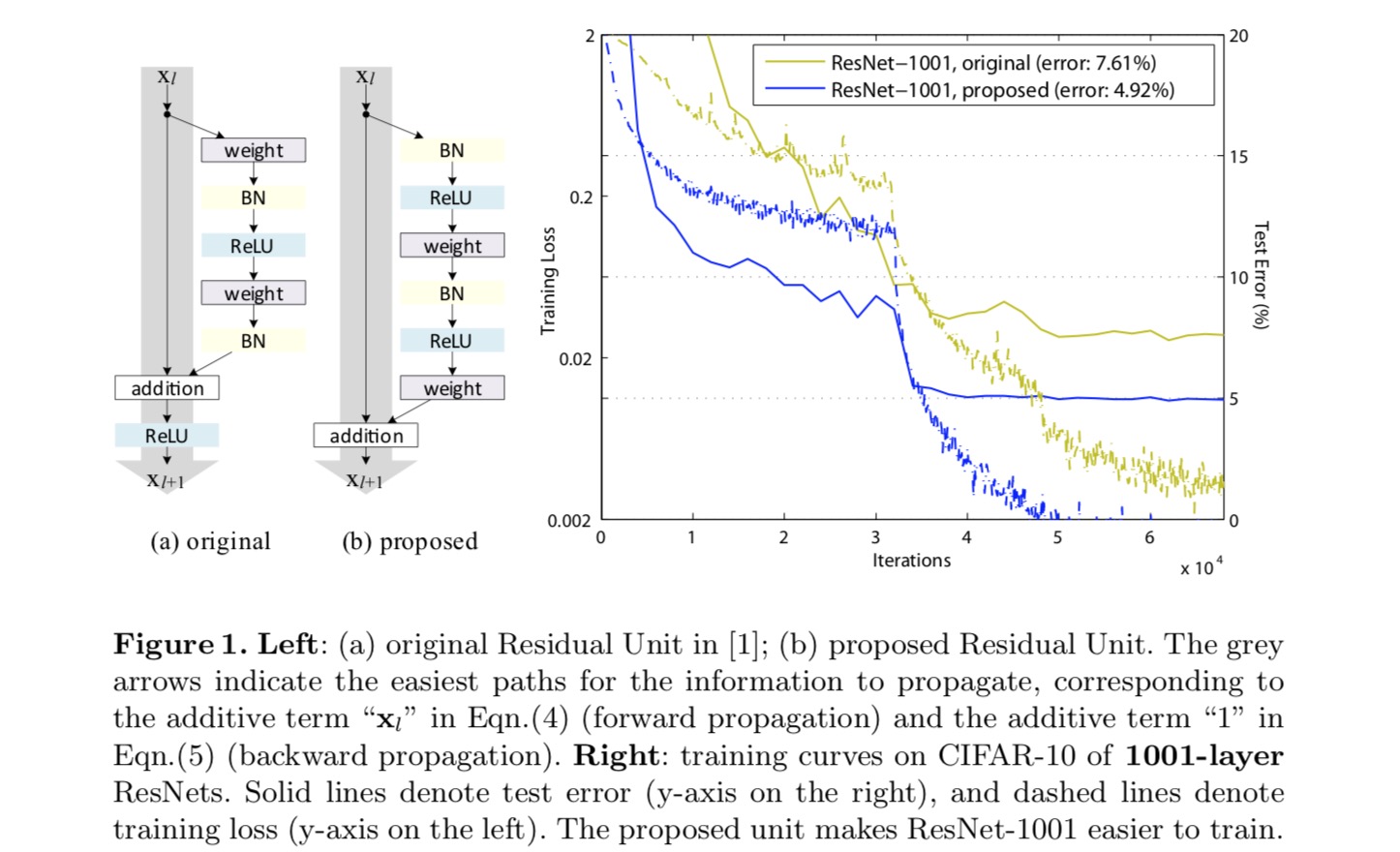
Analyse Av Dype Gjenværende nettverk

ResNets utviklet i det siste papiret er modulariserte arkitekturer som stabler byggeklosser av samme tilkoblingsform. I dette papiret kaller vi disse blokkene «Restenheter». Den opprinnelige Restenheten i det siste papiret utfører følgende beregning:

Her er inngangsfunksjonen til-Th Restenheten. er et sett med vekter (og skjevheter) knyttet til-Th Restenheten, og er antall lag I En Restenhet (er 2 eller 3 i det siste papiret). angir restfunksjonen, e.g. , en stabel med to 3×3 convolutional lag i det siste papiret. Funksjonen er operasjonen etter element-messig tillegg, og i det siste papiret Er ReLU. Funksjonen er satt som en identitetskartlegging: .

Hvis det også er en identitetskartlegging:, kan vi få:

Rekursivt vil vi ha:

for en dypere enhet og en grunnere enhet . Denne ligningen viser noen fineegenskaper. (1) funksjonen til en dypere enhet kan representeres som funksjonen til en hvilken som helst grunnere enhet pluss en restfunksjon i en form for, noe som indikerer at modellen er i restmote mellom noen enheter og . (2) funksjonen , av en dyp enhet, er summering av utgangene til alle foregående gjenværende funksjoner(pluss). Dette er i motsetning til et «vanlig nettverk» hvor en funksjon er en serie matrise-vektorprodukter, sier (ignorerer BN og ReLU).

ligningen ovenfor fører også til fine bakoverutbredelsesegenskaper. Betegner tapsfunksjonen som, fra kjederegelen for backpropagation har vi:

ovennevnte ligning indikerer at gradienten kan dekomponeres i to additive vilkår: et begrep som forplanter informasjon direkte uten hensyn til noen vektlag, og et annet begrep som forplanter seg gjennom vektlagene. Additiv sikt sikrer at informasjonen er direkte forplantet tilbake til en grunnere enhet l. ovennevnte ligning antyder også at det er usannsynlig for gradienten å bli kansellert ut for en mini-batch, fordi generelt begrepet ikke alltid kan være -1 for alle prøver i en mini-batch. Dette innebærer at gradienten av et lag ikke forsvinner selv når vektene er vilkårlig små.

de ovennevnte to ligningene antyder at signalet kan forplantes direkte fra en hvilken som helst enhet til en annen, både fremover og bakover. Grunnlaget for de første over to ligningene er to identitetstilordninger: (1) identitetsforskyvningsforbindelsen, og (2) betingelsen som er en identitetstilordning.

Betydningen av identitet hopp tilkoblinger

la oss vurdere en enkel modifikasjon,, å bryte identitet snarvei:

hvor er en modulerende skalar (for enkelhet vi fortsatt anta er identitet). Rekursivt å anvende denne formuleringen får vi en ligning som ligner den ovenfor:

hvor notasjonen absorberer skalarene i restfunksjonene. Tilsvarende har vi backpropagation av følgende form:

I Motsetning til forrige ligning, i denne ligningen er den første additiv termen modulert av en faktor . For et ekstremt dypt nettverk (er stort), hvis for alle , kan denne faktoren være eksponentielt stor; hvis for alle , kan denne faktoren være eksponentielt liten og forsvinne, noe som blokkerer backpropagated signalet fra snarveien og tvinger det til å strømme gjennom vektlagene. Dette resulterer i optimaliseringsproblemer som vi viser ved eksperimenter.

i analysen ovenfor erstattes den opprinnelige identity skip-tilkoblingen med en enkel skalering . Hvis hopp-tilkoblingen representerer mer kompliserte transformasjoner (for eksempel gating og 1×1-omveltninger), blir den første termen i ovennevnte ligning hvor er derivatet av . Dette produktet kan også hindre informasjonsformidling og hemme treningsprosedyren som vitne i følgende eksperimenter.

Eksperimenter På Skip-Tilkoblinger

vi eksperimenterer med 110-lags ResNet PÅ CIFAR-10. Denne ekstremt dype ResNet-110 har 54 tolags Restenheter (bestående av 3×3 convolutional lag) og er utfordrende for optimalisering. Ulike typer skip tilkoblinger er eksperimentert. Se følgende figur:

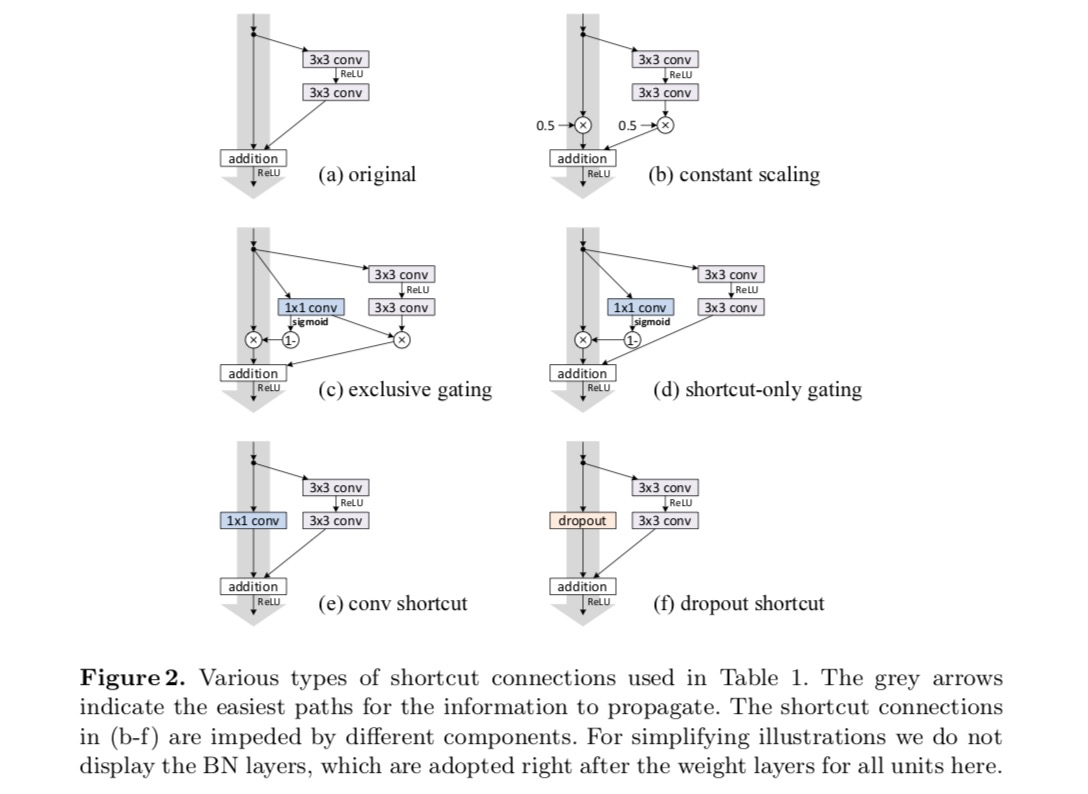
klassifiseringsresultatene vises i følgende tabell:

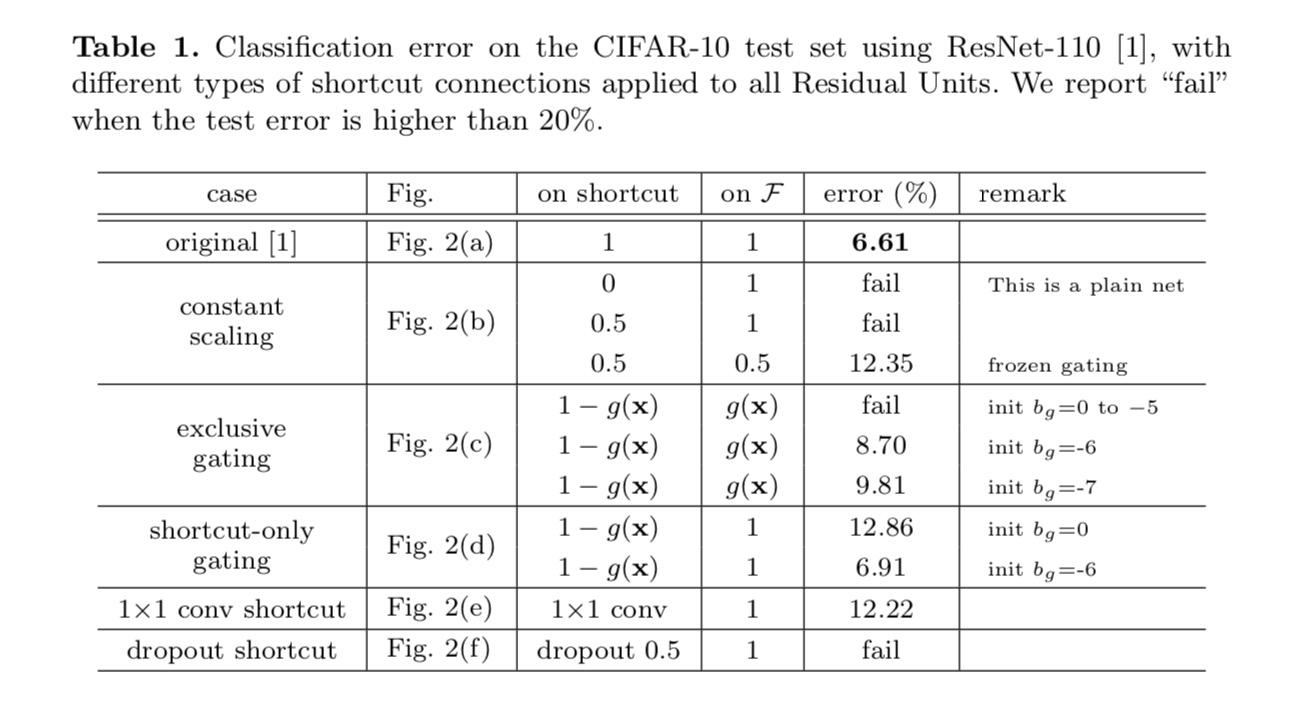
som angitt med de grå pilene i figuren ovenfor, er snarveisforbindelsene de mest direkte banene for informasjonen å forplante. Multiplikative manipulasjoner (skalering, gating, 1×1 viklinger og frafall) på snarveiene kan hemme informasjonsformidling og føre til optimaliseringsproblemer.

det er verdt å merke seg at gating og 1×1 convolutional snarveier innføre flere parametere, og bør ha sterkere representasjons evner enn identitet snarveier. Faktisk, snarvei-bare gating og 1×1 convolution dekke løsningen plass av identitet snarveier (dvs., de kan være optimalisert som identitet snarveier). Imidlertid er deres treningsfeil høyere enn for identitetsgenveier, noe som indikerer at nedbrytningen av disse modellene skyldes optimaliseringsproblemer, i stedet for representasjonsevner.

Bruk Av Aktiveringsfunksjoner

Eksperimenter i avsnittet ovenfor er under forutsetning av at etter-addisjon aktivering er identitetstilordning. Men i de ovennevnte forsokene er ReLU som utformet i det forste papiret. Deretter undersøker vi virkningen av .

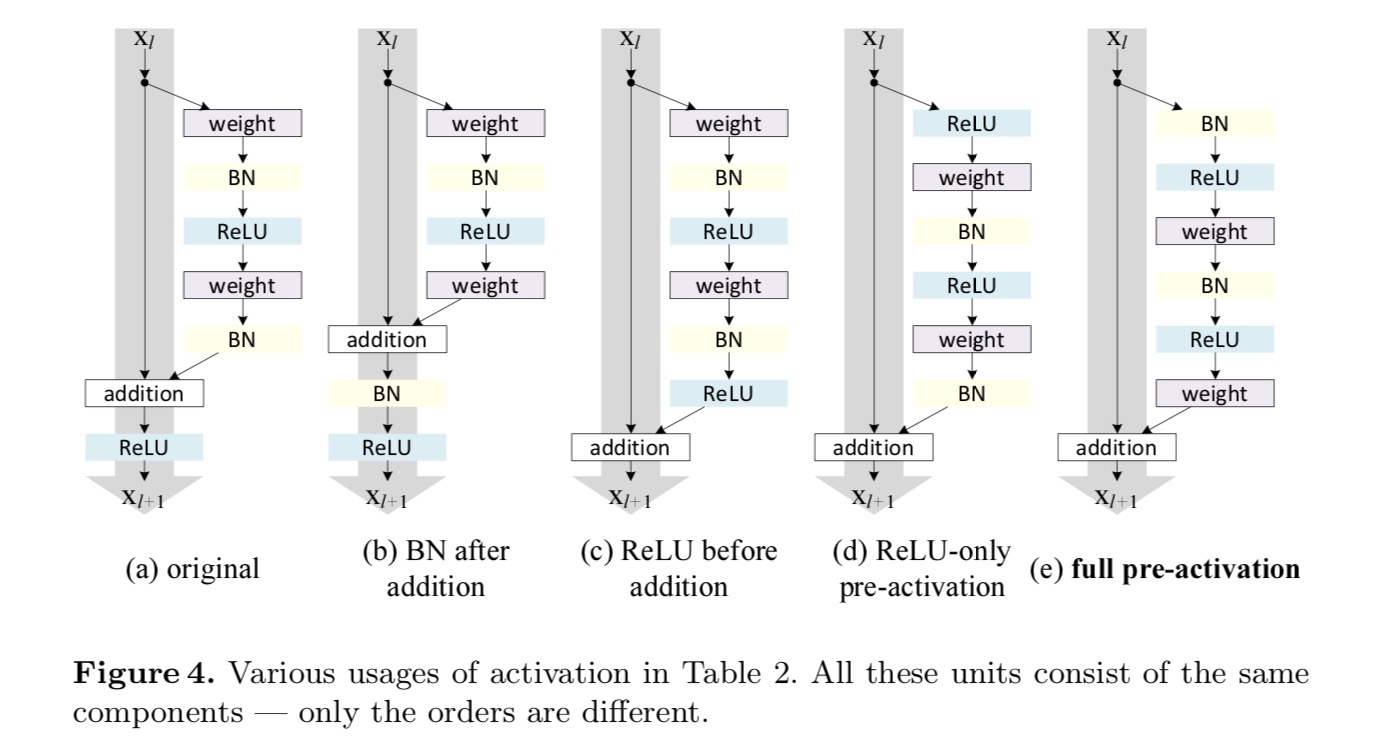
Vi ønsker å lage en identitetskartlegging, som gjøres ved å re-arrangere aktiveringsfunksjonene (ReLU og/ELLER BN, batch normalisering). I den følgende figuren har den opprinnelige Restenheten i det siste papiret en form I Fig. 4 (a – – BN brukes etter hvert vektlag, Og ReLU er vedtatt etter BN bortsett fra at den siste ReLU i En Restenhet er etter elementwise addisjon (=ReLU). Fig. 4 (b-e) viser alternativene vi undersøkte.

Eksperimenter på Aktivering

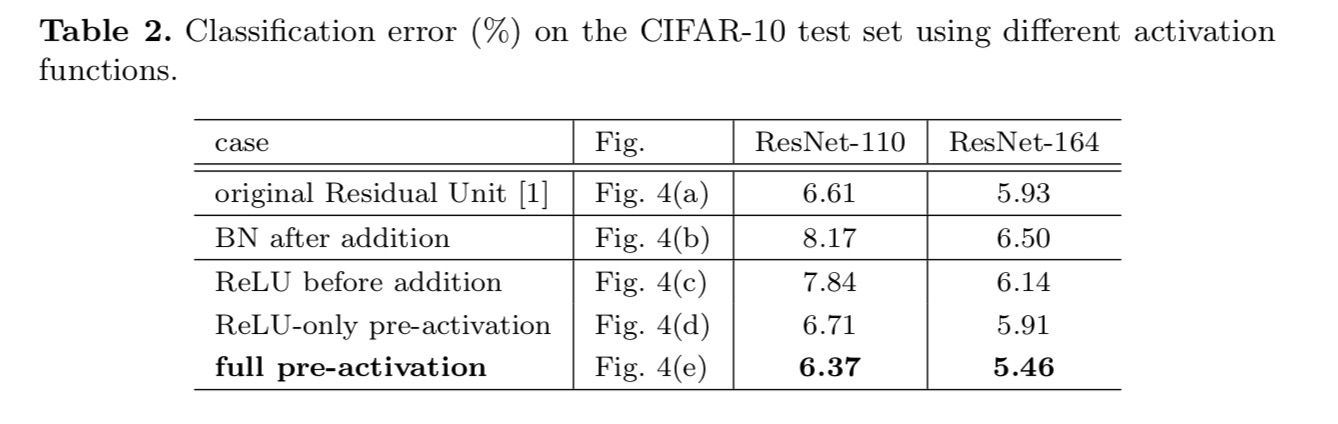
i denne delen eksperimenterer Vi med ResNet-110 og En 164-lags Flaskehalsarkitektur (betegnet Som ResNet-164). En flaskehals Restenhet består av et 1×1 lag for å redusere dimensjon, et 3×3 lag og et 1×1 lag for å gjenopprette dimensjon. Som utformet i det siste papiret, er beregningskompleksiteten lik den To-3×3 Restenheten.

Etter aktivering eller forhåndsaktivering?

i den opprinnelige utformingen påvirker aktiveringen begge banene i neste Restenhet: . Deretter utvikler vi en asymmetrisk form hvor en aktivering bare pavirker banen:, for noen . Ved å omdøpe notasjonene har vi følgende form:

for denne nye Restenheten som i ligningen ovenfor, blir den nye etter-addisjonsaktiveringen en identitetskartlegging. Denne utformingen betyr at hvis en ny etter-addisjon aktivering er asymmetrisk vedtatt, det tilsvarer recasting som pre-aktivering av neste Restenhet. Dette er illustrert i følgende figur:

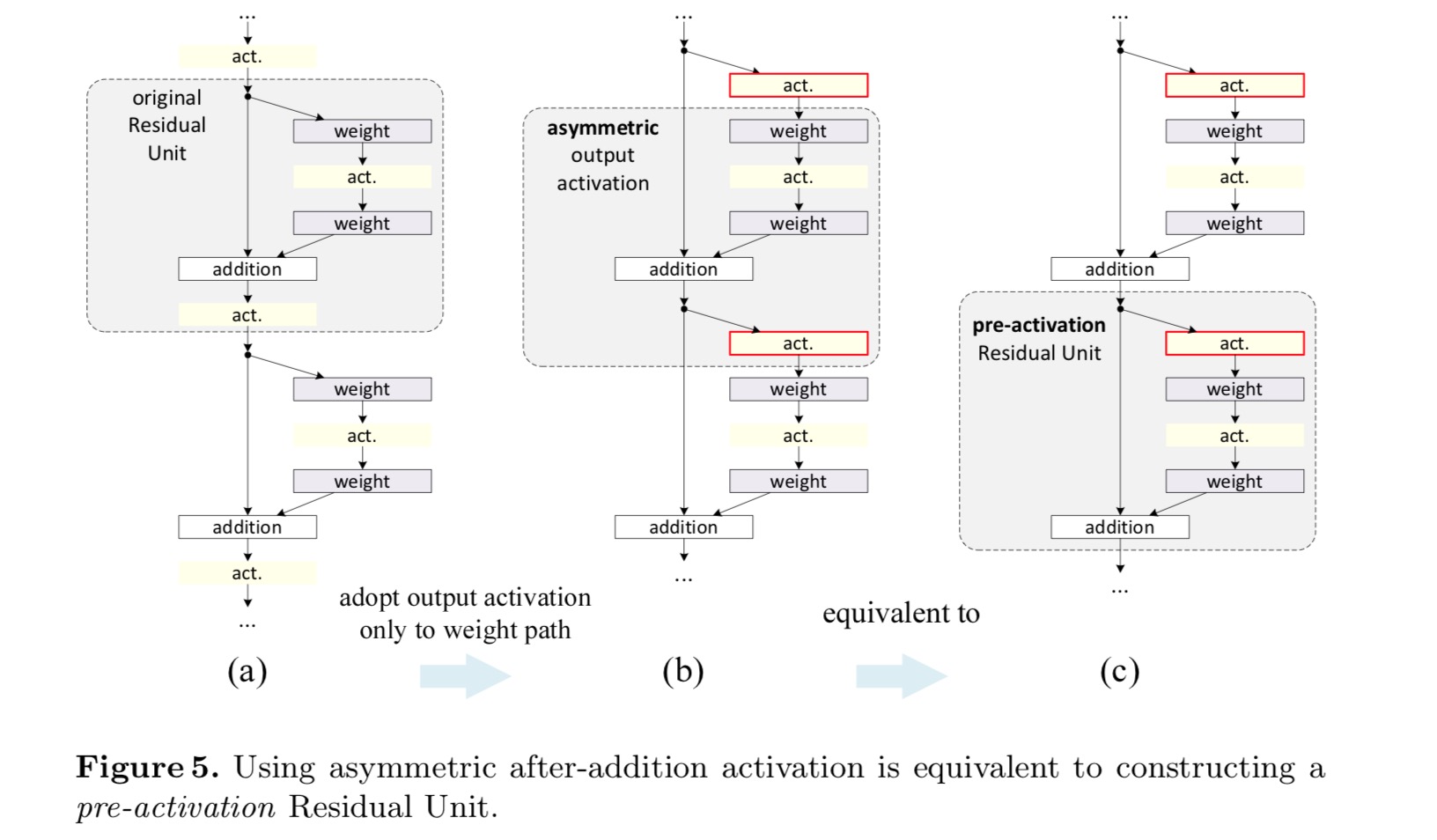
skillet mellom postaktivering / preaktivering skyldes tilstedeværelsen av element-wise tillegg. For et vanlig nettverk som har N-lag, er Det n-1-aktiveringer (Bn / ReLU), og det spiller ingen rolle om vi tenker på dem som post – eller pre-aktiveringer. Men for forgrenede lag fusjonert ved tillegg, er aktiveringsposisjonen viktig. De Ulike bruksområder for aktivering vises I Figur 4.

vi eksperimenterer med to slike design: (1) ReLU-only preaktivering og (2) full preaktivering hvor BN og ReLU begge er vedtatt før vektlag. På en eller annen måte overraskende, NÅR BN og ReLU begge brukes som forhåndsaktivering, blir resultatene forbedret med sunne marginer. For det første blir optimaliseringen ytterligere lettet (sammenlignet med baseline ResNet) fordi f er en identitetskartlegging. For det andre, ved hjelp AV BN som pre-aktivering forbedrer regularisering av modellene.

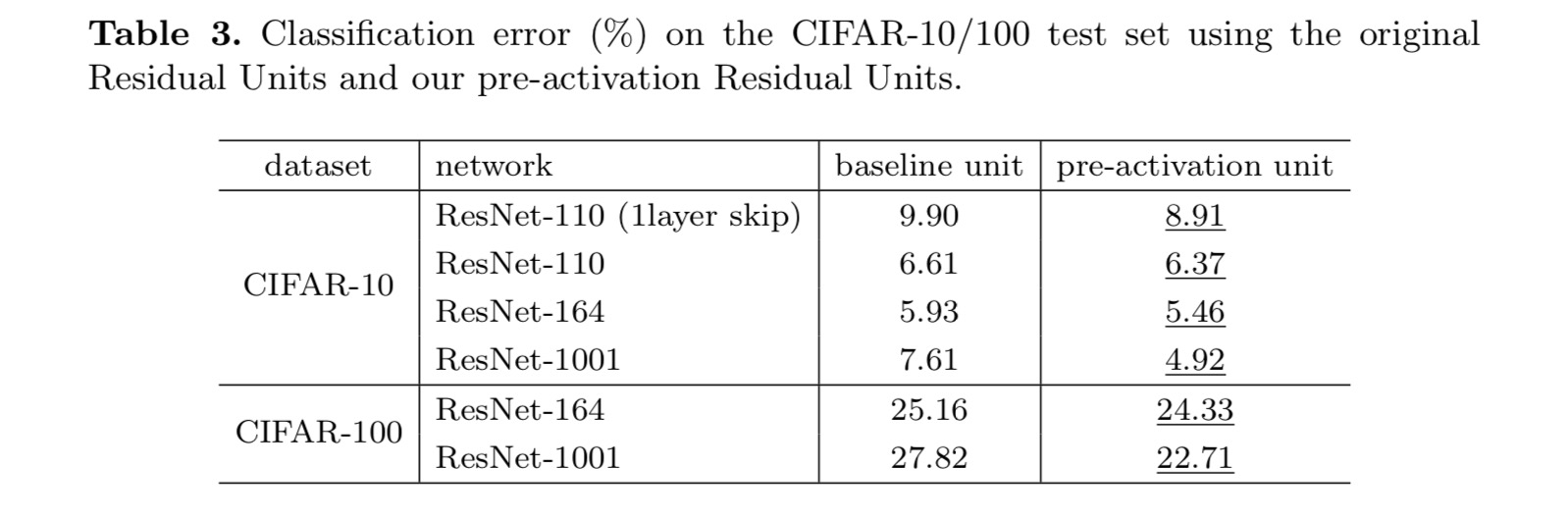
Konklusjon

denne artikkelen undersøker forplantningsformuleringene bak forbindelsesmekanismene til dype gjenværende nettverk. Våre avledninger innebærer at identitets snarveier og aktivering av identitet etter tillegg er avgjørende for å gjøre informasjonsutbredelsen jevn. Ablation eksperimenter demonstrere phenom-ena som er i samsvar med våre avledninger. Vi presenterer også 1000-lags dype nettverk som lett kan trent og oppnå forbedret nøyaktighet.

Aggregert Rest Transformasjon For Dype Nevrale Nettverk

Introduksjon

forskning på visuell anerkjennelse gjennomgår en overgang fra» feature engineering «til»network engineering». Menneskelig innsats har blitt flyttet til å designe bedre nettverksarkitekturer for å lære representasjoner.

Designarkitekturer blir stadig vanskeligere med det økende antall hyper-parametere, spesielt når det er mange lag. VGG-nettene viser en enkel, men effektiv strategi for å bygge svært dype nettverk: stabling av byggeklosser av samme form. Denne strategien er arvet Av ResNets som stabler moduler av samme topologi. Denne enkle regelen reduserer frie valg av hyper parametere, og dybde er eksponert som en viktig dimensjon i nevrale nettverk. Videre argumenterer vi for at enkelheten i denne regelen kan redusere risikoen for overjustering av hyperparametrene til et bestemt datasett. Robustheten TIL VGG-nett og ResNets har blitt bevist av ulike visuelle gjenkjenningsoppgaver og av ikke-visuelle oppgaver som involverer tale og språk.I Motsetning TIL VGG-nets har Inception-Modellene vist at nøye utformede topologier er i stand til å oppnå overbevisende nøyaktighet med lav teoretisk kompleksitet. Inception-modellene har utviklet seg over tid, men en viktig felles egenskap er en split-transform-merge-strategi. I En Inception-modul blir inngangen delt inn i noen få lavere dimensjonale innbygginger (med 1×1-omveltninger), forvandlet av et sett med spesialiserte filtre (3×3, 5×5 osv.), og fusjonert ved sammenkobling. Split-transform-merge-oppførselen Til Inception-moduler forventes å nærme seg representasjonskraften til store og tette lag, men med en betydelig lavere beregningskompleksitet.

Til tross for god nøyaktighet har realiseringen av Inception modeller blitt ledsaget av en rekke kompliserende faktorer. Selv om forsiktige kombinasjoner av disse komponentene gir gode nevrale nettverksoppskrifter, er det generelt uklart hvordan Man tilpasser Inception-arkitekturene til nye datasett / oppgaver,spesielt når det er mange faktorer og hyper-parametere som skal utformes.i dette papiret presenterer vi en enkel arkitektur som vedtar VGG / ResNets ‘ strategi for å gjenta lag, mens du utnytter split-transform-merge-strategien på en enkel, utvidbar måte. En modul i vårt nettverk utfører et sett med transformasjoner, hver på en lavdimensjonal embedding, hvis utganger aggregeres ved summering. Vi forfølger en enkel realisering av denne ideen — transformasjonene som skal aggregeres, er alle av samme topologi. Denne utformingen tillater oss å utvide til et stort antall transformasjoner uten spesialiserte design.vi demonstrerer empirisk at våre aggregerte transformasjoner overgår Den opprinnelige ResNet-modulen, selv under den begrensede tilstanden for å opprettholde beregningskompleksitet og modellstørrelse. Vi understreker at selv om det er relativt enkelt å øke nøyaktigheten ved å øke kapasiteten (gå dypere eller bredere), er metoder som øker nøyaktigheten samtidig som man opprettholder (eller reduserer) kompleksiteten sjeldne i litteraturen.

vår metode indikerer at kardinalitet (størrelsen på settet av transformasjoner) er en konkret, målbar dimensjon som er av sentral betydning, i tillegg til dimensjonene av bredde og dybde. Eksperimenter viser at økende kardinalitet er en mer effektiv måte å oppnå nøyaktighet på enn å gå dypere eller bredere, spesielt når dybde og bredde begynner å gi avtagende avkastning for eksisterende modeller.Våre nevrale nettverk, Kalt ResNeXt (foreslår neste dimensjon), overgår ResNet-101/152, ResNet-200, Inception-v3 og Inception-ResNet-v2 på ImageNet-klassifiseringsdatasettet. Spesielt Er En 101-lags ResNeXt i stand til å oppnå bedre nøyaktighet Enn ResNet-200, men har bare 50% kompleksitet. Dess, ResNeXt utstillinger betydelig enklere design enn alle Inception modeller.

Metode

vi adopterer en svært modularisert design etter VGG / ResNets. Vårt nettverk består av en stabel med gjenværende blokker. Disse blokkene har samme topologi, og er underlagt to enkle regler inspirert AV VGG/ResNets: (1) hvis de produserer romlige kart av samme størrelse, deler blokkene de samme hyperparametrene (bredde og filterstørrelser), og (2) hver gang det romlige kartet er nedsamplet med en faktor på 2, multipliseres bredden på blokkene med en faktor på 2. Den andre regelen sikrer at beregningskompleksiteten, I Form Av FLOPs (flyttallsoperasjoner, i #av multipliser-legger til), er omtrent det samme for alle blokker.

med disse to reglene trenger vi bare å designe en malmodul, og alle moduler i et nettverk kan bestemmes tilsvarende. Så disse to reglene sterkt begrense design plass og tillate oss å fokusere på noen viktige faktorer. Nettverkene konstruert av disse reglene er I Tabell 1.

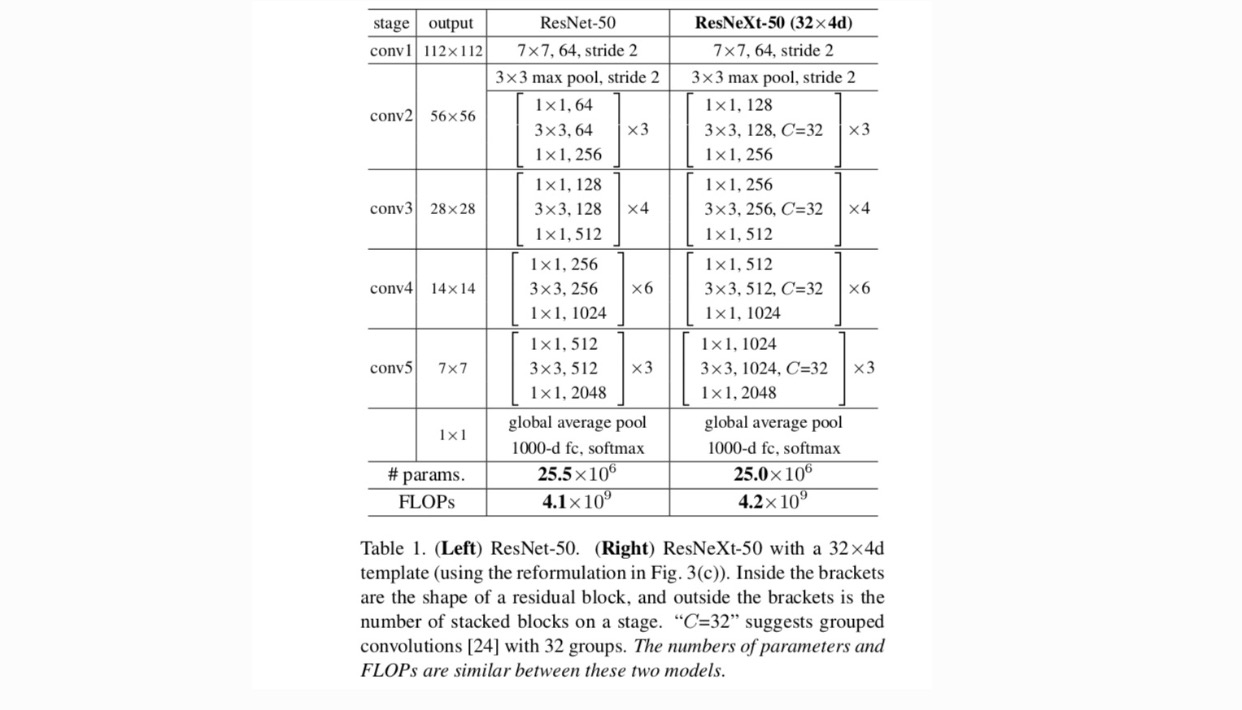
de enkleste nevronene i kunstige nevrale nettverk utfører indre produkt (vektet sum), som er den elementære transformasjonen gjort av fullt tilkoblede og innviklede lag.

operasjonen ovenfor kan omarbeides som en kombinasjon av splitting, transformering og aggregering. (1): Splitting: vektoren er skåret som en lavdimensjonal embedding, og i det ovennevnte er det et enkeltdimensjonalt underrom (2) Transformering: den lavdimensjonale representasjonen er transformert, og i det ovennevnte er det ganske enkelt skalert: (3) Aggregering: transformasjonene i alle embedninger aggregeres av .

Gitt den ovennevnte analysen av en enkel neuron, vurderer vi å erstatte elementær transformasjon (w_i, x_i) med en mer generisk funksjon, som i seg selv også kan være et nettverk. Formelt presenterer vi aggregerte transformasjoner som:

hvor kan være en vilkårlig funksjon. Analogt med en enkel nevron, bør projisere inn i en (eventuelt lavdimensjonal) embedding og deretter transformere den.

vi refererer til som kardinalitet. er i en posisjon som ligner på in, men trenger ikke lik og kan være et vilkårlig tall. Vi viser ved eksperimenter at kardinalitet er en viktig dimensjon og kan være mer effektiv enn dimensjonene av bredde og dybde.

i dette papiret vurderer vi en enkel måte å designe transformasjonsfunksjonene på: alle har samme topologi. Dette utvider VGG-stilstrategien for å gjenta lag av samme form. Vi satte den individuelle transformasjonen til å være flaskehalsformet arkitektur illustrert I Fig. 1 (høyre). I dette tilfellet produserer det første 1×1-laget i hver den lavdimensjonale embedding.

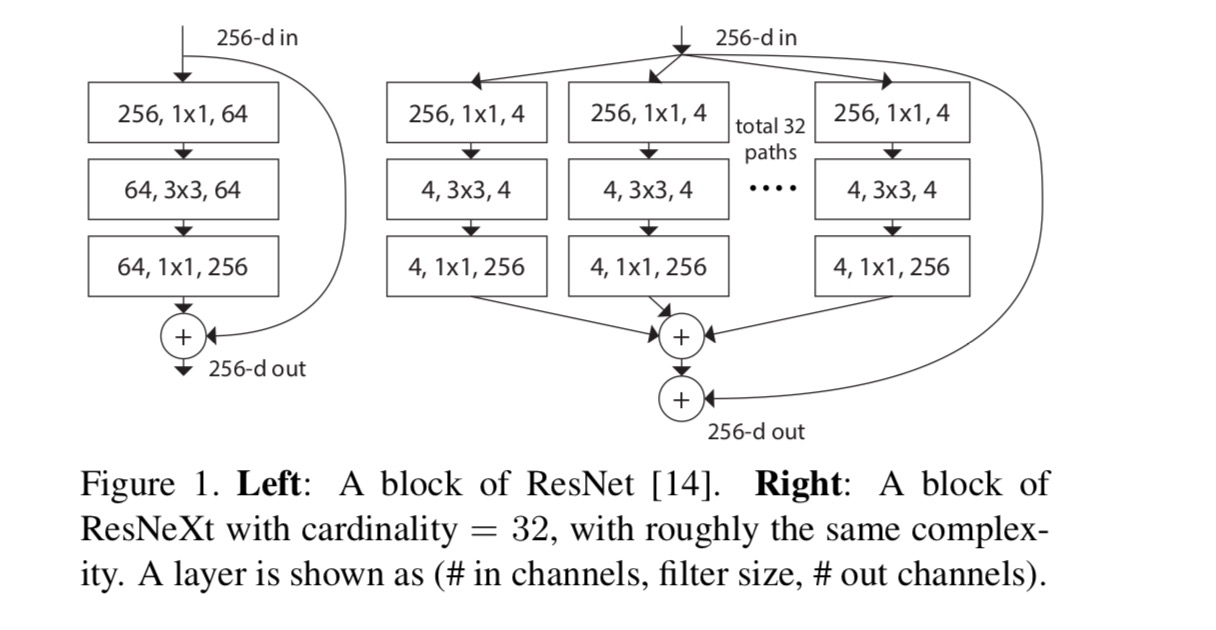
den aggregerte transformasjonen i siste ligning tjener som gjenværende funksjon:

hvor er utgangen.

relasjonene Mellom ResNeXt og Inception-ResNet / Gruppert-Convolutions er vist i følgende figur:

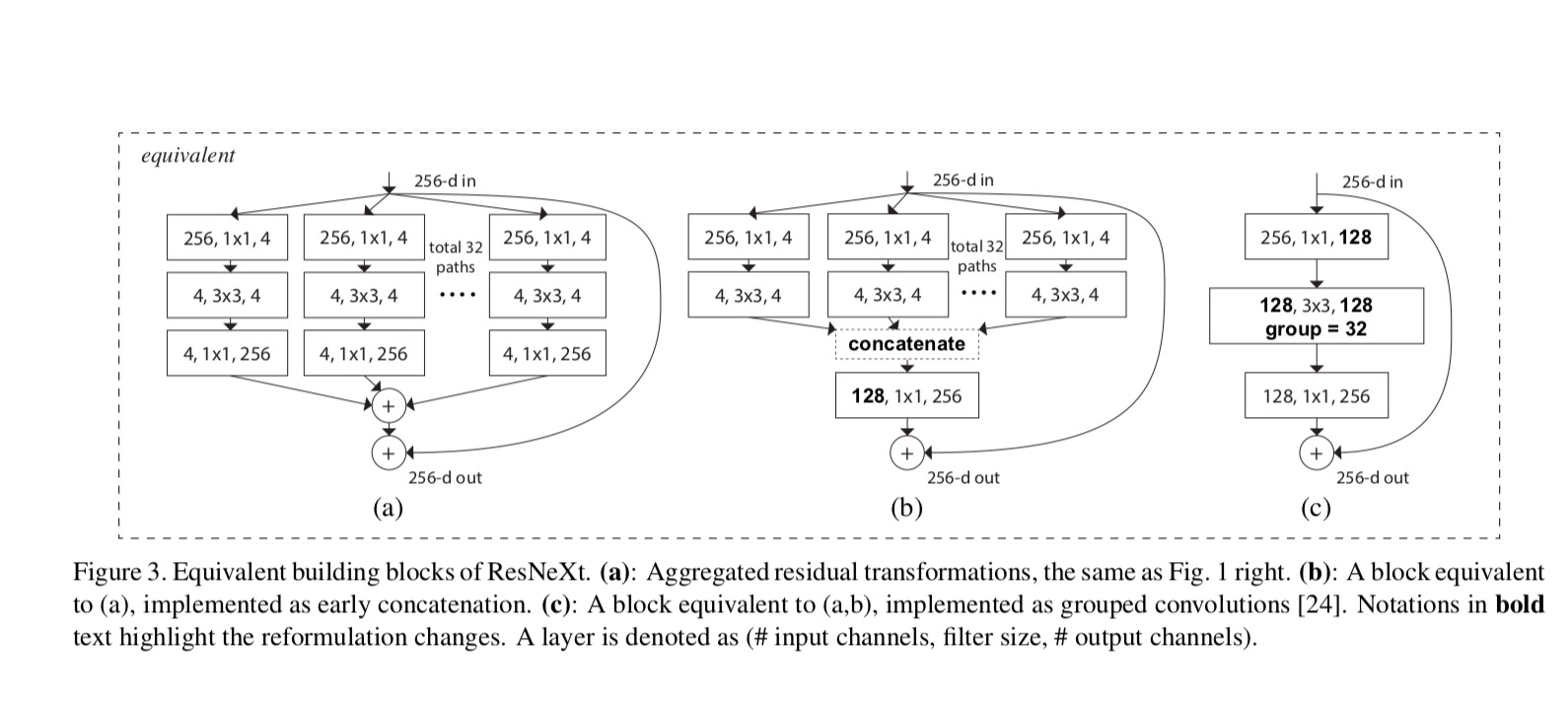
når vi vurderer forskjellige kardinaliteter samtidig som kompleksiteten opprettholdes, vil vi minimere modifikasjonen av andre hyper-parametere. 4-d I Fig 1 (høyre)), fordi den kan isoleres fra inngangen og utgangen av blokken. Denne strategien introduserer ingen endring til andre hyper-parametere (dybde eller input/output bredde av blokker), så er nyttig for oss å fokusere på virkningen av kardinalitet.

I Fig. 1 (venstre), den opprinnelige ResNet-flaskehalsblokken har parametere og proporsjonale Flopper (på samme funksjonskartstørrelse). Med flaskehalsbredde, vår mal I Fig. 1 (høyre) har: parametere og proporsjonale Flopper. Nar og, dette nummeret . Tabellen nedenfor viser forholdet mellom kardinalitet og flaskehalsbredde.

Eksperimenter

Kardinalitet vs Bredde. Vi vurderer først avviket mellom kardinalitet og flaskehalsbredde, under bevart kompleksitet som oppført i Tabell 2. Tabell 3 viser resultatene. Sammenligning Med ResNet-50 har 32×4d ResNeXt-50 en valideringsfeil på 22,2%, som er 1,7% lavere Enn ResNet baseline er 23,9%. Med kardinalitet øker fra 1 til 32 mens du holder kompleksiteten, holder feilraten redusert. Videre har 32×4d ResNeXt også en mye lavere treningsfeil enn ResNet countetpart, noe som tyder på at gevinsten ikke kommer fra regularisering, men fra sterkere representasjoner.

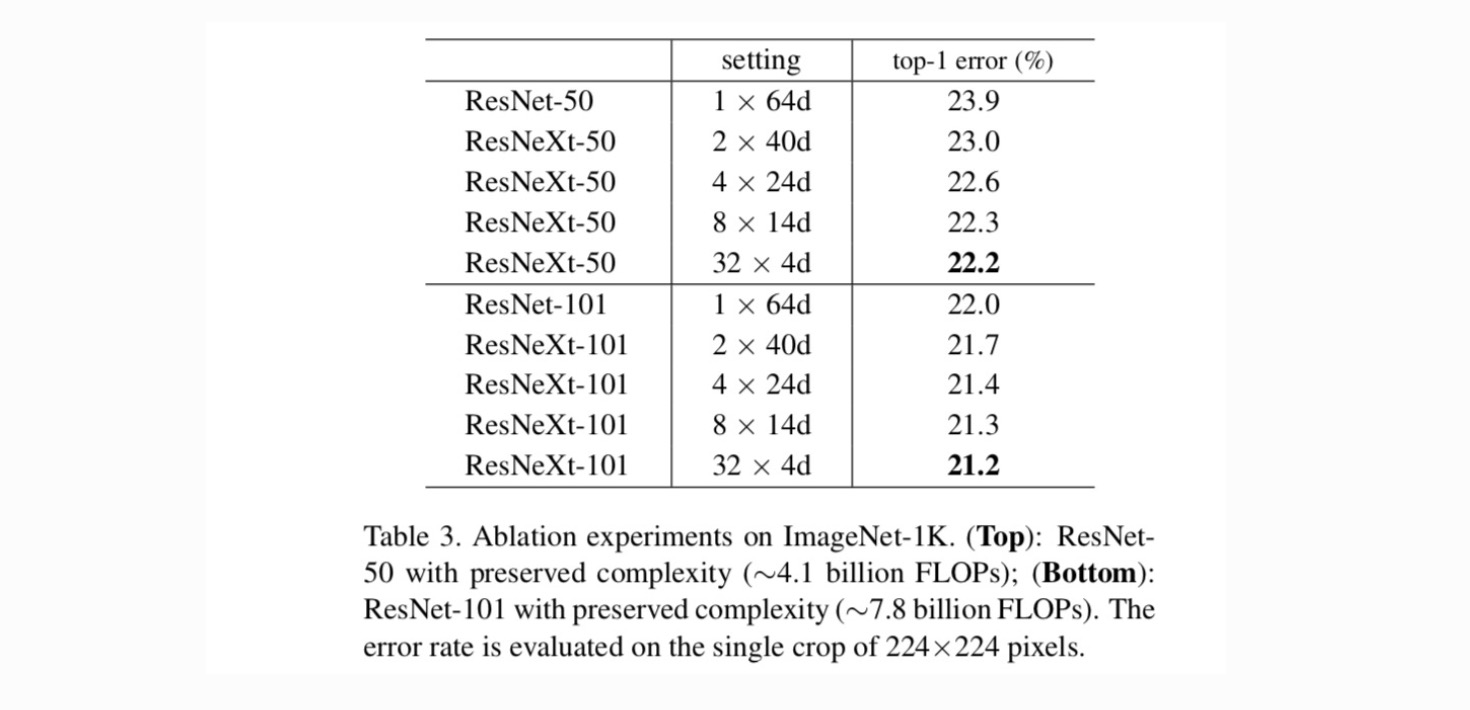
Økende Kardinalitet vs. Dypere/Bredere.Neste vi undersøke økende kompleksitet ved å øke kardinalitet C eller økende dybde eller bredde. Vi sammenligner følgende varianter (1)går dypere til 200 lag. Vi adopterer ResNet-200. (2) går bredere ved å øke flaskehalsen bredde. (3) Økende kardinalitet ved å doble C.

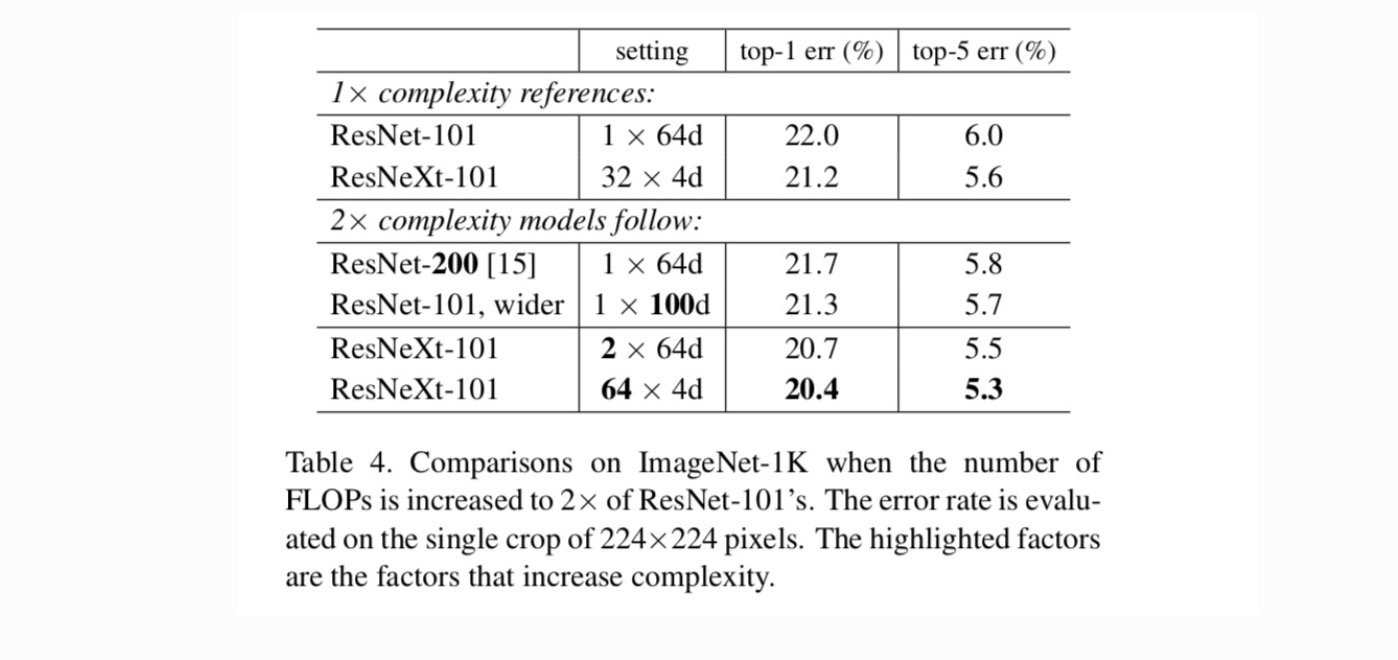
Tabell 4 viser at økende kompleksitet med 2× konsekvent reduserer feil vs. resnet-101 baseline (22,0%). Men forbedringen er liten når du går dypere (ResNet-200, med 0.3%) eller bredere (bredere ResNet-101, med 0.7%). Tvert imot viser økende kardinalitet C mye bedre resultater enn å gå dypere eller bredere.

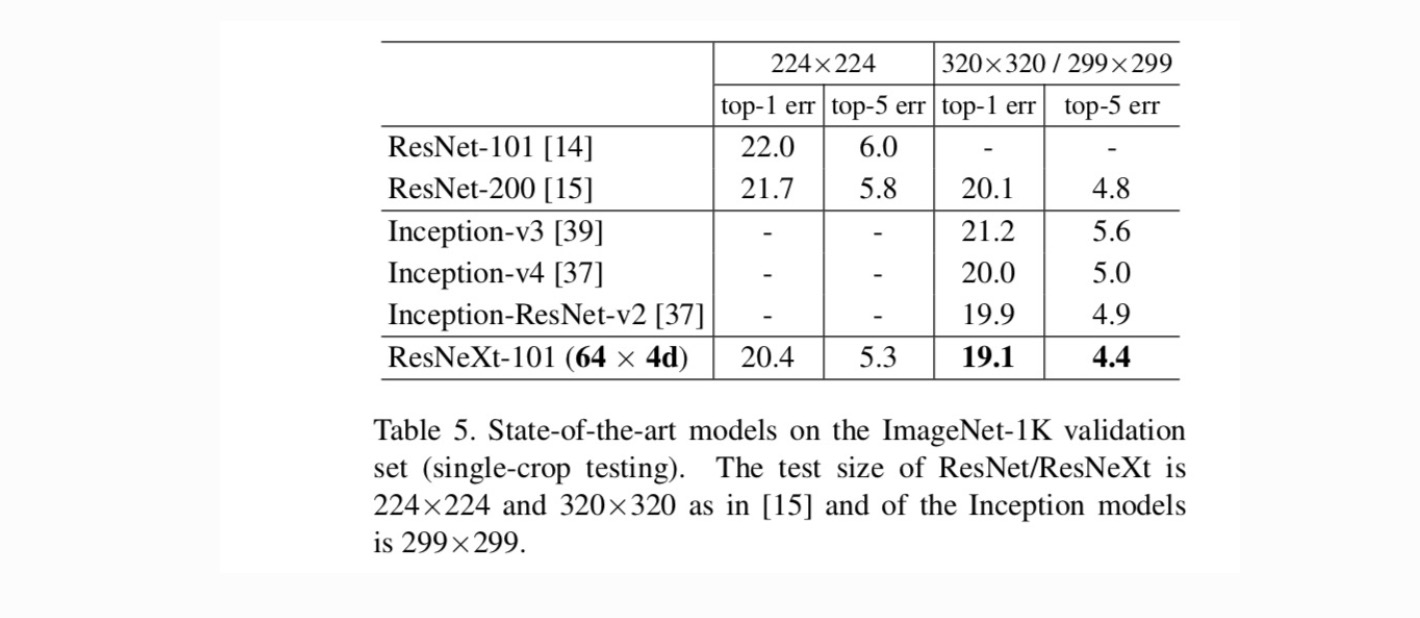
Sammenligninger med toppmoderne resultater. Tabell 5 viser flere resultater av enkeltavlingstesting på ImageNet-valideringssettet. Våre resultater sammenligner gunstig Med ResNet, Inception-v3 / v4 og Inception-ResNet-v2, og oppnår en single-crop top – 5 feilrate på 4,4%. I tillegg er vår arkitekturdesign mye enklere enn Alle Inception-modeller, og krever betydelig færre hyper-parametere som skal settes for hånd.