
Maskinlæring brukes til slutt å forutsi utfall gitt et sett med funksjoner. Derfor er alt vi kan gjøre for å generalisere ytelsen til vår modell sett på som en nettogevinst. Dropout er en teknikk som brukes til å hindre en modell fra overfitting. Dropout fungerer ved tilfeldig å sette utgående kanter av skjulte enheter (nevroner som utgjør skjulte lag) til 0 ved hver oppdatering av treningsfasen. Hvis Du ser På Keras-dokumentasjonen for dropout-laget, ser Du en lenke til Et hvitt papir skrevet Av Geoffrey Hinton and friends, som går inn i teorien bak dropout.
I forsøkseksemplet bruker Vi Keras til å bygge et nevralt nettverk med mål om å gjenkjenne håndskrevne sifre.
from keras.datasets import mnist
from matplotlib import pyplot as plt
plt.style.use('dark_background')
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation, Dropout
from keras.utils import normalize, to_categorical
Vi bruker Keras til å importere dataene til vårt program. Dataene er allerede delt inn i trenings-og testsettene.
(X_train, y_train), (X_test, y_test) = mnist.load_data()
La oss ta en titt for å se hva vi jobber med.
plt.imshow(x_train, cmap = plt.cm.binary)
plt.show()

/ div>
etter at vi er ferdig med å trene modell, bør den kunne gjenkjenne det forrige bildet som en fem.
Det er en liten forbehandling som vi må utføre på forhånd. Vi normaliserer pikslene (funksjonene) slik at de varierer fra 0 til 1. Dette vil gjøre det mulig for modellen å konvergere mot en løsning som mye raskere. Deretter forvandler vi hver av måletikettene for en gitt prøve til en rekke 1s og 0s hvor indeksen til tallet 1 indikerer sifferet bildet representerer. Vi gjør dette fordi ellers vår modell ville tolke sifferet 9 som å ha en høyere prioritet enn tallet 3.
X_train = normalize(X_train, axis=1)
X_test = normalize(X_test, axis=1)
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
Uten Frafall
før vi mater en 2-dimensjonal matrise inn i et nevralt nettverk, bruker vi et flatt lag som forvandler det til et 1-dimensjonalt array ved å legge hver påfølgende rad til den som gikk foran den. Vi skal bruke to skjulte lag bestående av 128 nevroner hver og et utgangslag bestående av 10 nevroner, hver for en av de 10 mulige sifrene. Softmax-aktiveringsfunksjonen returnerer sannsynligheten for at en prøve representerer et gitt siffer.

siden vi prøver å forutsi klasser, bruker vi kategorisk crossentropi som vår tapsfunksjon. Vi måler ytelsen til modellen ved hjelp av nøyaktighet.
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
vi setter 10% av dataene til side for validering. Vi vil bruke dette til å sammenligne tendensen til en modell for å overfit med og uten utfall. En batchstørrelse på 32 innebærer at vi vil beregne gradienten og ta et skritt i retning av gradienten med en størrelse som er lik læringshastigheten, etter å ha passert 32 prøver gjennom nevrale nettverk. Vi gjør dette totalt 10 ganger som angitt av antall epoker.
history = model.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

div>
vi kan plotte trenings-og valideringsnøyaktighetene i hver epoke ved å bruke historikkvariabelen returnert av fit-funksjonen.
som du kan se, uten frafall, stopper valideringstapet etter den tredje epoken.

As you can see, without dropout, the validation accuracy tends to plateau around the third epoch.

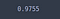
Using this simple model, we still managed to obtain an accuracy of over 97%.
test_loss, test_acc = model.evaluate(X_test, y_test)
test_acc
dropout
det er noen debatt om hvorvidt dropout skal plasseres før eller etter aktiveringsfunksjonen. Som en tommelfingerregel, plasser frafallet etter aktiveringsfunksjonen for alle andre aktiveringsfunksjoner enn relu. Ved passering av 0,5 er hver skjult enhet (neuron) satt til 0 med en sannsynlighet på 0,5. Med andre ord, det er en 50% endring at utgangen av en gitt nevron vil bli tvunget til 0.

igjen, siden vi prøver å forutsi klasser, bruker vi kategorisk crossentropi som vår tapsfunksjon.
model_dropout.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
ved å gi parameteren validations split, vil modellen sette fra seg en brøkdel av treningsdataene og evaluere tapet og eventuelle modellberegninger på disse dataene på slutten av hver epoke. Hvis premisset bak frafallet holder, bør vi se en merkbar forskjell i valideringsnøyaktigheten i forhold til forrige modell. Shuffle-parameteren vil blande treningsdataene før hver epoke.
history_dropout = model_dropout.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

som du kan se, er valideringstapet betydelig lavere enn det som er oppnådd ved bruk av vanlig modell.

som du kan se, konvergerte modellen mye raskere og oppnådde en nøyaktighet på nær 98% på valideringssettet, mens den forrige modellen plateaued rundt den tredje epoken.

nøyaktigheten oppnådd på testsettet er ikke veldig annerledes enn den som er oppnådd fra modellen uten utfall. Dette er sannsynligvis på grunn av det begrensede antall prøver.
test_loss, test_acc = model_dropout.evaluate(X_test, y_test)
test_acc

avsluttende tanker
dropout kan hjelpe en modell generalisere ved tilfeldig å sette utgangen for en gitt neuron til 0. Ved å sette utgangen til 0 blir kostnadsfunksjonen mer følsom for naboneuroner som endrer måten vektene vil bli oppdatert under prosessen med backpropagation.