Hva Er EN ARIMAX-Modell?

Hva er ARIMAX-modellen?

hvis du har lest vår serie med bloggopplæringer om modeller for estimering av tidsseriedata, er du allerede kjent med 3 store tilnærminger-autoregression , glidende gjennomsnitt og integrasjon.

Hva er det vanlige temaet i alle disse modellene?

de stod utelukkende på en enkelt variabel.

en modell kan imidlertid også ta hensyn til mer enn bare tidligere priser eller tidligere rester.

og disse er de såkalte «MAX» – modellene, MED ARMAX som den ikke-integrerte versjonen og ARIMAX – den integrerte ekvivalenten.

Så i denne opplæringen skal vi utforske hvordan de ser ut og vise deg hvordan du implementerer Dem i Python trinnvis.

La oss komme i gang, skal vi?

Hvorfor KALLES ARMAX Og ARIMAX «MAX» – Modeller?

navnene ARMAX og ARIMAX kommer som utvidelser av HENHOLDSVIS ARMA og ARIMA. X lagt til slutten står for «eksogen». Med andre ord foreslår det å legge til en separat annen ekstern variabel for å måle vår endogene variabel.

ARMAX-Og ARIMAX-Modellligningen:

Siden den eneste forskjellen MELLOM ARMAX og ARIMAX er at DEN ene er integrert og den andre ikke er, kan vi undersøke en av dem og deretter markere hvordan den andre vil variere.

vi utforsket en integrert modell i VÅR siste bloggartikkel (ARIMA), så la oss se hvordan ARIMAX-ligningen ser ut.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

selvfølgelig, ligningen for ARMAX ville være den samme, bortsett fra at vi ville bruke den faktiske variable, si Side, i stedet for sin delta.

Pt=c+ßX+ϕ1 Pt-1+ θ1 ϵ

Å Bryte NED ARIMAX-Ligningen:

VI kan tenke PÅ ARMAX som et spesielt tilfelle av ARIMAX, der integrasjonsrekkefølgen er 0.

Så, for resten av opplæringen, vil vi fokusere på ARIMAX.

Og vi begynner med å bryte ned de forskjellige delene i den. For det første representerer Pt og Pt-1 verdiene i henholdsvis den nåværende perioden og 1 periode siden.

tilsvarende er ϵ og ϵ-1 feilvilkårene for de samme to periodene. Og selvfølgelig er c bare en baseline konstant faktor.

de to parameterne, ϕ1 og θ1, uttrykker hvilke deler av verdien Pt-1 og feil ϵ-1 siste periode som er relevante for å estimere den nåværende.

Nå er de to nye tilleggene til modellen «X» og dens koeffisient β. Akkurat som ϕ er β en koeffisient som vil bli estimert basert på modellvalg og data. Men Hva Med X?

Hva er en eksogen variabel?

Vel, X Er den eksogene variabelen, Og Det kan være hvilken som helst variabel vi er interessert i.

det kan være en tidsvarierende måling som inflasjonsraten eller prisen på en annen indeks. Eller en kategorisk variabel som skiller de forskjellige dagene i uken. Det kan også være En Boolsk regnskap for de spesielle festlige perioder. Til slutt kan det stå for en kombinasjon av flere forskjellige eksterne faktorer.tanken er at det kan være en hvilken som helst annen variabel eller variabler som kan påvirke prisene, så lenge vi har tilgjengelige data.

slike ytre faktorer er kjent som eksogene variabler i vår regresjon. Vi bruker deres verdier til å forutsi og forklare den vi er interessert i, som skjer for å være dagens priser i vårt tilfelle.

Hvordan Implementere ARMAX Og ARIMAX Modeller I Python?

praktisk nok kommer statsmodels-pakken inn med EN metode som kalles ARIMA, som er fullt i stand til å håndtere slike ekstra innganger.

Vi starter med å spesifisere modellegenskapene og ordrene til modellen:

etter at vi har gjort det, må vi også spesifisere det eksogene argumentet kalt «exog».

verdien vi ønsker å passere må være en rekke av noe slag siden vi ønsker å ha verdier knyttet til hver tidsperiode.

for eksempel kan Vi bruke S&p priser som denne eksogene variabelen, siden vi allerede har dem i våre data.

nå er vi klare til å passe EN ARIMAX (1,1,1) modell.

sørg for å navngi modellvariabelen på en måte som skiller den fra lignende modeller. I dette tilfellet velger vi å gjøre dette ved å legge Til «X, spx» på slutten for å indikere at den eksogene variabelen Er S &P.

så, som det fremgår av utdrag, setter vi dette lik ARIMA-metoden som før, vi legger til tidsserien og rekkefølgen, som vi er vant til. Til slutt, mellom de to, setter vi» exog «argumentet lik » DF SPX», som indikerer s&p priser.

hvis vi passer til denne modellen og skriver ut sammendragstabellen, skal vi se at Vi får en ekstra rad For S & p priser.

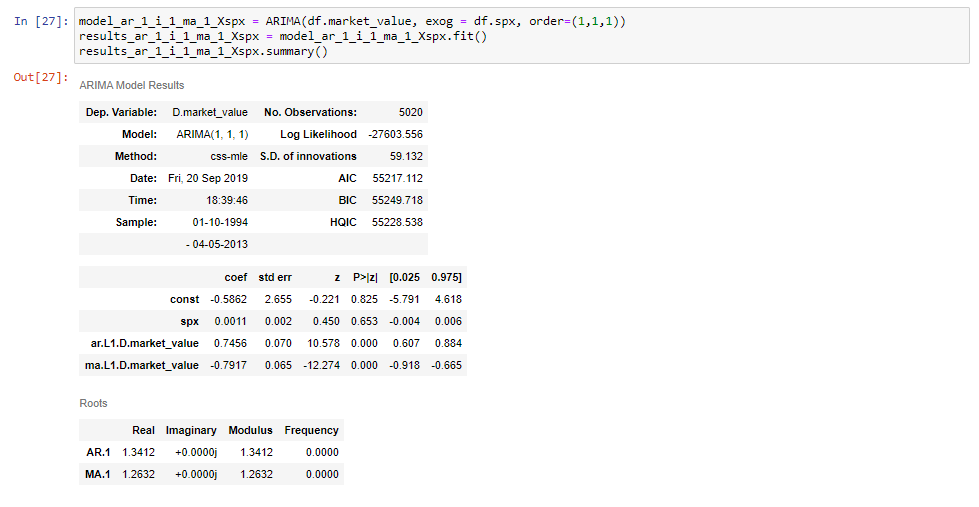
og det er alt som skal til!

Vi har sett hvordan vi implementerer EN ARIMAX-modell i Python.

hvis du vil lære mer OM ARIMAX og andre tidsseriemodeller I Python, må du sjekke ut våre trinnvise Python-opplæringsprogrammer. Hvis Du er ny På Python, og du er entusiastisk til å lære mer, vil denne omfattende artikkelen om å lære Python programmering veilede deg hele veien fra installasjonen, Gjennom Python Ide, Biblioteker og rammer, til De beste Python karriereveiene og jobbutsiktene.

Klar Til å ta neste skritt mot en karriere innen datavitenskap?

Sjekk ut Det komplette Datavitenskapsprogrammet i dag. Start med det grunnleggende med Våre Statistikk, Matematikk og Excel kurs. Bygg opp en trinnvis opplevelse med SQL, Python, R, Power BI og Tableau. Og oppgrader ferdighetene dine med Maskinlæring, Dyp Læring, Kredittrisikomodellering, Tidsserieanalyse og Kundeanalyse I Python. Fortsatt ikke sikker på at du vil gjøre din interesse for datavitenskap til en karriere? Du kan utforske læreplanen eller registrere deg for 15 timer med nybegynner til avansert videoinnhold gratis ved å klikke på knappen nedenfor.